
Master Chemical Kinetics Class 12 Questions and Answers for Higher Marks
Chemical kinetics class 12 is the branch of chemistry concerned with the study of the rates of chemical reactions and the factors that influence them. Chemical Kinetics Class 12 NCERT Solutions helps students delve into the intricacies of chemical kinetics, exploring topics such as rate of reaction, factors affecting rate, and methods of determining reaction rates. Understanding chemical kinetics is crucial from industrial processes to environmental studies, as it provides insights into reaction mechanisms and enables the optimisation of reaction conditions. Chemical kinetics solutions equips students with essential knowledge to comprehend and analyse chemical reactions quantitatively.
 Table of Content
Table of ContentCheck out the Revised Class 12 Chemistry Syllabus and get started with Vedantu!
Quick Insights of Class 12 Chemical Kinetics NCERT solutions-
NCERT Solutions for Class 12 Chemistry Chapter 3 will give you insights into the General Introduction: The chemical kinetics chapter will give you insight into the Rate of a reaction , factors affecting the rate of reaction.
The section will give you crisp learnings on concentration, temperature, catalyst; order and molecularity of a reaction, rate law and specific rate constant, integrated rate equations and half-life.
The understanding related to topics like the concept of collision theory, activation energy, Arrhenius equation.
Using these solutions can help students analyse their level of preparation and understanding of concepts.
Class 12 chemistry chemical kinetics NCERT solutions topics are included according to the revised syllabus for the academic year 2025-26.
It also provides resources such as class notes, important concepts, and formulas exemplar solutions.
Master Chemical Kinetics Class 12 Questions and Answers for Higher Marks
1. For the reaction $\text{R}\to \text{P}$, the concentration of a reactant changes from 0.03 M to 0.02 M in 25 minutes. Calculate the average rate of reaction using units of time both in minutes and seconds.
Ans: The average rate of the reaction can be calculated by dividing the change in the rate of decreasing the rate of reactant by the time taken. This is given below:
\[\text{Average rate = - }\frac{\text{ }\!\!\Delta\!\!\text{ }\!\![\!\!\text{ R }\!\!]\!\!\text{ }}{\text{ }\!\!\Delta\!\!\text{ t}}\]
This can be written as:
\[\text{Average rate = - }\frac{{{\text{ }\!\![\!\!\text{ R }\!\!]\!\!\text{ }}_{\text{2}}}\text{- }\!\![\!\!\text{ R}{{\text{ }\!\!]\!\!\text{ }}_{\text{1}}}}{{{\text{t}}_{\text{2}}}\text{-}{{\text{t}}_{\text{1}}}}\]
\[{{\text{R}}_{\text{1}}}\text{ = 0}\text{.03 M}\]
\[{{\text{R}}_{2}}\text{ = 0}\text{.02 M}\]
\[{{\text{t}}_{\text{2}}}\text{ - }{{\text{t}}_{\text{1}}}\text{ = 25 min}\]
Putting the values, we get:
\[\text{Average rate = - }\frac{0.02-0.03}{25}\]
\[\text{Average rate = - }\frac{-0.01}{25}=4\text{ }\!\!\times\!\!\text{ 1}{{\text{0}}^{-4}}\text{ M mi}{{\text{n}}^{-1}}\]
So, the average rate in minutes will be $4\text{ }\!\!\times\!\!\text{ 1}{{\text{0}}^{-4}}\text{ M mi}{{\text{n}}^{-1}}$
Now, to find the average rate in seconds we have to divide the above answer by 60. So, the answer will be:
\[\text{Average rate = - }\frac{4\text{ }\!\!\times\!\!\text{ 1}{{\text{0}}^{-4}}\text{ }}{60}=\text{ 6}\text{. 66 }\!\!\times\!\!\text{ 1}{{\text{0}}^{-6}}\text{ M }{{\text{s}}^{-1}}\]
Therefore, the average rate in seconds will be $6.66\text{ }\!\!\times\!\!\text{ 1}{{\text{0}}^{-6}}\text{ M }{{\text{s}}^{-1}}$
2. In a reaction, 2A $\to $ Products, the concentration of A decreases from $\text{0}\text{.5 mol }{{\text{L}}^{\text{-1}}}$ to $\text{0}\text{.4 mol }{{\text{L}}^{\text{-1}}}$ in 10 minutes. Calculate the rate during this interval.
Ans: The average rate of the reaction can be calculated by dividing the change in the rate of decreasing the rate of reactant by the time taken. This is given below:
\[\text{Average rate = - }\frac{1}{2}\frac{\text{ }\!\!\Delta\!\!\text{ }\!\![\!\!\text{ A }\!\!]\!\!\text{ }}{\text{ }\!\!\Delta\!\!\text{ t}}\]
This is due the fact that the reaction given is:
2A $\to $ Products
So, the average rate will be written as:
\[\text{Average rate = - }\frac{1}{2}\frac{{{\text{ }\!\![\!\!\text{ A }\!\!]\!\!\text{ }}_{\text{2}}}\text{- }\!\![\!\!\text{ A}{{\text{ }\!\!]\!\!\text{ }}_{\text{1}}}}{{{\text{t}}_{\text{2}}}\text{-}{{\text{t}}_{\text{1}}}}\]
\[{{\text{A}}_{\text{1}}}\text{ = 0}\text{.5 M}\]
\[{{\text{A}}_{2}}\text{ = 0}\text{.4 M}\]
\[{{\text{t}}_{\text{2}}}\text{ - }{{\text{t}}_{\text{1}}}\text{ = 10 min}\]
Putting the values, we get:
\[\text{Average rate = - }\frac{1}{2}\text{ }\!\!\times\!\!\text{ }\frac{0.4-0.5}{10}\]
\[\text{Average rate = - }\frac{1}{2}\text{ }\!\!\times\!\!\text{ }\frac{-0.1}{10}=5\text{ }\!\!\times\!\!\text{ 1}{{\text{0}}^{-3}}\text{ M mi}{{\text{n}}^{-1}}\]
So, the average rate will be $\text{5 }\!\!\times\!\!\text{ 1}{{\text{0}}^{-3}}\text{ M mi}{{\text{n}}^{-1}}$
3. For a reaction, $\text{A + B }\to \text{ Product}$, the rate law is given by: $\text{r = k }\!\![\!\!\text{ A}{{\text{ }\!\!]\!\!\text{ }}^{\text{1/2}}}\text{ }\!\![\!\!\text{ B}{{\text{ }\!\!]\!\!\text{ }}^{\text{2}}}$. What is the order of the reaction?
Ans: The order of the reaction can be calculated by adding the stoichiometry coefficients of the reactants in the given rate of the reaction.
Given the rate is $\text{r = k }\!\![\!\!\text{ A}{{\text{ }\!\!]\!\!\text{ }}^{\text{1/2}}}\text{ }\!\![\!\!\text{ B}{{\text{ }\!\!]\!\!\text{ }}^{\text{2}}}$
So, the order will be:
\[\text{Order = 2 + }\frac{\text{1}}{\text{2}}\text{ = 2}\text{.5}\]
So, the order of the reaction is 2.5.
4. The conversion of the molecules X to Y follows second order kinetics. If concentration of x is increased to three times how will it affect the rate of formation of Y?
Ans: The reaction will be:
\[\text{X }\to \text{ Y}\]
As the question says that this reaction follows the second order reaction, we can write the rate law equation as:
\[\text{Rate = k }\!\![\!\!\text{ X}{{\text{ }\!\!]\!\!\text{ }}^{\text{2}}}\text{ = k}{{\text{a}}^{\text{2}}}\]
If [X] = a mol/ L
It is said that the concentration of X increases by three times, so we can write:
[X] = 3a mol/ L
Therefore, the rate of reaction will be:
\[\text{Rate = k (3a}{{\text{)}}^{\text{2}}}\text{ = 9 k}{{\text{a}}^{\text{2}}}\]
Thus, the rate of the reaction will increase by 9 times or the rate formation will increase by 9 times.
5. A first order reaction has a rate constant $\text{1}\text{.15 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-3}}}\text{ }{{\text{s}}^{\text{-1}}}$. How long will 5 g reactant take to reduce to 3 g?
Ans: The initial amount of the reactant is given as 5 g. We can write:
\[{{\text{ }\!\![\!\!\text{ R }\!\!]\!\!\text{ }}_{\text{0}}}\text{ = 5 g}\]
The final amount of the reactant is given as 3 g. We can write:
[R] = 3 g
We are also given the value of rate constant as:
\[\text{Rate constant = 1}\text{.15 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-3}}}\text{ }{{\text{s}}^{\text{-1}}}\]
We know that the reaction is a 1st order reaction, the time can be calculated by:
\[\text{t = }\frac{\text{2}\text{.303}}{\text{k}}\text{ log}\frac{{{\text{ }\!\![\!\!\text{ R }\!\!]\!\!\text{ }}_{\text{0}}}}{\text{ }\!\![\!\!\text{ R }\!\!]\!\!\text{ }}\]
Putting the values in the above formula, we get:
\[\text{t = }\frac{\text{2}\text{.303}}{1.15\text{ x 1}{{\text{0}}^{-3}}}\text{ log}\frac{5}{3}\]
\[\text{t = }\frac{\text{2}\text{.303}}{1.15\text{ }\!\!\times\!\!\text{ 1}{{\text{0}}^{-3}}}\text{ }\!\!\times\!\!\text{ 0}\text{.2219}\]
t = 444 seconds
So, the time taken will be 444 seconds.
6. Time required to decompose $\text{S}{{\text{O}}_{\text{2}}}\text{C}{{\text{l}}_{\text{2}}}$ to half its initial amount is 60 minutes. If the decomposition is a first order reaction, calculate the rate constant of the reaction.
Ans: We are given that the decomposition of $\text{S}{{\text{O}}_{\text{2}}}\text{C}{{\text{l}}_{\text{2}}}$ is a first order reaction. So, we can write:
\[{{\text{t}}_{\text{1/2}}}\text{ = }\frac{\text{0}\text{.693}}{\text{k}}\]
It is mentioned that the time required for the initial amount to become half is 60 minutes.
\[{{\text{t}}_{\text{1/2}}}\text{ = 60 min}\]
Therefore, $\text{k = }\frac{\text{0}\text{.693}}{{{\text{t}}_{\text{1/2}}}}$
Putting the value, we get:
\[\text{k = }\frac{\text{0}\text{.693}}{\text{60 }\!\!\times\!\!\text{ 60}}\text{ = 1}\text{.925 }\!\!~\!\!\text{ }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-4}}}\text{ }{{\text{s}}^{\text{-1}}}\]
Thus, the rate constant is $\text{1}\text{.925 }\!\!~\!\!\text{ }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-4}}}\text{ }{{\text{s}}^{\text{-1}}}$.
7. What will be the effect of temperature on rate constant?
Ans: An increase of 10 degrees in temperature causes a reaction's rate constant to almost double in size. In any case, the Arrhenius equation gives the exact temperature dependency of a chemical reaction rate.
The Arrhenius equation is given below:
\[\text{k = A }{{\text{e}}^{\text{-}{{\text{E}}_{\text{a}}}\text{/Rt}}}\]
Where, A is the Arrhenius factor or the frequency factor,
T is the temperature,
R is the gas constant,
${{\text{E}}_{\text{a}}}$ is the activation energy.
8. The rate of the chemical reaction doubles for an increase of 10 K in absolute temperature from 298 K. Calculate ${{\text{E}}_{\text{a}}}$.
Ans: The formula that can be used to solve the question is:
\[\text{log}\frac{{{\text{k}}_{\text{1}}}}{{{\text{k}}_{\text{2}}}}\text{ = }\frac{{{\text{E}}_{\text{a}}}}{\text{2}\text{.303R}}\left[ \frac{{{\text{T}}_{\text{2}}}\text{-}{{\text{T}}_{\text{1}}}}{{{\text{T}}_{\text{1}}}{{\text{T}}_{\text{2}}}} \right]\]
${{\text{T}}_{\text{1}}}$ temperature given is absolute temperature and it is equal to 298 K.
${{\text{T}}_{2}}$ = 298 + 10 = 308 K
It is given that the rate of the chemical reaction double for an increase of 10 K, therefore, we can write the values of rate constant as:
\[{{\text{k}}_{\text{1}}}\text{ = x}\]
\[{{\text{k}}_{\text{2}}}\text{ = 2x}\]
Also, $\text{R = 8}\text{.314 J }{{\text{K}}^{\text{-1}}}\text{ mo}{{\text{l}}^{\text{-1}}}$
Now, putting all the values in the formula, we get:
\[\text{log}\frac{\text{2x}}{\text{x}}\text{ = }\frac{{{\text{E}}_{\text{a}}}}{\text{2}\text{.303 }\!\!\times\!\!\text{ 8}\text{.314}}\left[ \frac{\text{10}}{\text{298 }\!\!\times\!\!\text{ 308}} \right]\]
\[\text{log2 = }\frac{{{\text{E}}_{\text{a}}}}{\text{2}\text{.303 }\!\!\times\!\!\text{ 8}\text{.314}}\left[ \frac{\text{10}}{\text{298 }\!\!\times\!\!\text{ 308}} \right]\]
\[{{\text{E}}_{\text{a}}}\text{ = }\frac{2.303\text{ }\!\!\times\!\!\text{ 8}\text{.314 }\!\!\times\!\!\text{ 298 }\!\!\times\!\!\text{ 308 }\!\!\times\!\!\text{ log 2}}{10}\]
\[{{\text{E}}_{\text{a}}}\text{ = 52897}\text{.78 J mo}{{\text{l}}^{-1}}\]
\[{{\text{E}}_{\text{a}}}\text{ = 52}\text{.89 kJ mo}{{\text{l}}^{-1}}\]
9. The activation energy for the reaction $\text{2H}{{\text{I}}_{\text{(g)}}}\to {{\text{H}}_{\text{2}}}_{_{\text{(g)}}}\text{+}{{\text{I}}_{\text{2}}}_{_{\text{(g)}}}$ is $\text{209}\text{.5 kJ mo}{{\text{l}}^{\text{-1}}}$ at 581 K. Calculate the fraction of molecules of molecules having energy equal to or greater than activation energy.
Ans: We are given the activation energy as $\text{209}\text{.5 kJ mo}{{\text{l}}^{\text{-1}}}$
T = 581 K
\[\text{R = 8}\text{.314 J }{{\text{K}}^{\text{-1}}}\text{ mo}{{\text{l}}^{\text{-1}}}\]
Now, the fraction of molecules of reactants having energy equal to or greater than activation energy is given as:
\[\text{x = }{{\text{e}}^{{{\text{E}}_{\text{a}}}\text{/RT}}}\]
\[\text{ln x =}\frac{\text{-}{{\text{E}}_{\text{a}}}}{\text{RT}}\]
\[\text{log x =}\frac{\text{-}{{\text{E}}_{\text{a}}}}{\text{2}\text{.303 RT}}\]
\[\text{log x =}\frac{209500}{\text{2}\text{.303 }\!\!\times\!\!\text{ 8}\text{.314 }\!\!\times\!\!\text{ 581}}\text{ }=\text{ }18.8323\]
Now, taking the antilog:
x = Antilog (18.8323)
\[\text{x = 1}\text{.471 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-19}}}\]
NCERT Exercise
1. From the rate expression for the following reactions, determine their order of reaction and the dimension of the rate constants.
(i). $\text{3 NO(g) }\to {{\text{N}}_{\text{2}}}\text{O(g) Rate = k }\!\![\!\!\text{ NO}{{\text{ }\!\!]\!\!\text{ }}^{\text{2}}}$
Ans: We are given:
\[\text{Rate = k }\!\![\!\!\text{ NO}{{\text{ }\!\!]\!\!\text{ }}^{\text{2}}}\]
From this we can see that the order of the reaction = 2
\[\text{k = }\frac{\text{rate}}{{{\text{ }\!\![\!\!\text{ No }\!\!]\!\!\text{ }}^{\text{2}}}}\]
Dimensions will be:
\[\text{k = }\frac{\text{mol }{{\text{L}}^{\text{-1}}}\text{ }{{\text{s}}^{\text{-1}}}}{{{\text{(mol }{{\text{L}}^{\text{-1}}}\text{)}}^{\text{2}}}}\]
\[\text{=}\frac{\text{mol }{{\text{L}}^{\text{-1}}}\text{ }{{\text{s}}^{\text{-1}}}}{\text{mo}{{\text{l}}^{\text{2}}}\text{ }{{\text{L}}^{\text{2}}}}\]
\[\text{= L mo}{{\text{l}}^{\text{-1}}}\text{ }{{\text{s}}^{\text{-1}}}\]
(ii).${{\text{H}}_{\text{2}}}{{\text{O}}_{\text{2}}}\text{(aq)+3}{{\text{I}}^{\text{-}}}\text{(aq)+2}{{\text{H}}^{\text{+}}}\to \text{2}{{\text{H}}_{\text{2}}}\text{O(l)+I}_{\text{3}}^{\text{-}}\text{ Rate=k }\!\![\!\!\text{ }{{\text{H}}_{\text{2}}}{{\text{O}}_{\text{2}}}\text{ }\!\!]\!\!\text{ }\!\![\!\!\text{ }{{\text{I}}^{\text{-}}}\text{ }\!\!]\!\!\text{ }$
Ans: Ans: \[Rate =k[{{H}_{2}}{{O}_{2}}][{{I}^{-}}]\]
From this we can see that the order of the reaction = 2
\[k=\frac{rate}{[{{H}_{2}}{{O}_{2}}][{{I}^{-}}]}\]
Dimensions will be:
\[\text{k = }\frac{\text{mol }{{\text{L}}^{\text{-1}}}\text{ }{{\text{s}}^{\text{-1}}}}{{{\text{(mol }{{\text{L}}^{\text{-1}}}\text{)}}^{\text{2}}}}\]
\[\text{=}\frac{\text{mol }{{\text{L}}^{\text{-1}}}\text{ }{{\text{s}}^{\text{-1}}}}{\text{mo}{{\text{l}}^{\text{2}}}\text{ }{{\text{L}}^{\text{2}}}}\]
\[\text{= L mo}{{\text{l}}^{\text{-1}}}\text{ }{{\text{s}}^{\text{-1}}}\]
(iii). $\text{C}{{\text{H}}_{\text{3}}}\text{CHO(g)}\to \text{C}{{\text{H}}_{\text{4}}}\text{(g)+ CO(g) Rate = k }\!\![\!\!\text{ C}{{\text{H}}_{\text{3}}}\text{CHO}{{\text{ }\!\!]\!\!\text{ }}^{\text{3/2}}}$
Ans: \[\text{Rate = k }\!\![\!\!\text{ C}{{\text{H}}_{3}}CHO{{]}^{3/2}}\]
From this we can see that the order of the reaction = $\frac{3}{2}$
\[\text{k = }\frac{\text{rate}}{{{\text{ }\!\![\!\!\text{ C}{{\text{H}}_{3}}CHO]}^{\frac{3}{2}}}}\]
Dimensions will be:
\[\text{k = }\frac{\text{mol }{{\text{L}}^{\text{-1}}}\text{ }{{\text{s}}^{\text{-1}}}}{{{\text{(mol }{{\text{L}}^{\text{-1}}}\text{)}}^{3/2}}}\]
\[\text{=}\frac{\text{mol }{{\text{L}}^{\text{-1}}}\text{ }{{\text{s}}^{\text{-1}}}}{\text{mo}{{\text{l}}^{\frac{3}{2}}}\text{ }{{\text{L}}^{\frac{3}{2}}}}\]
\[\text{= }{{\text{L}}^{\frac{1}{2}}}\text{ mo}{{\text{l}}^{\text{-}\frac{1}{2}}}\text{ }{{\text{s}}^{\text{-1}}}\]
(iv). ${{\text{C}}_{\text{2}}}{{\text{H}}_{\text{5}}}\text{Cl(g)}\to {{\text{C}}_{\text{2}}}{{\text{H}}_{\text{4}}}\text{(g)+ HCl(g) Rate = k }\!\![\!\!\text{ }{{\text{C}}_{\text{2}}}{{\text{H}}_{\text{5}}}\text{Cl }\!\!]\!\!\text{ }$
Ans: \[\text{Rate = k }\!\![\!\!\text{ }{{\text{C}}_{2}}{{H}_{5}}Cl]\]
From this we can see that the order of the reaction = 1
\[\text{k = }\frac{\text{rate}}{\text{ }\!\![\!\!\text{ }{{\text{C}}_{2}}{{H}_{5}}Cl]}\]
Dimensions will be:
\[\text{k = }\frac{\text{mol }{{\text{L}}^{\text{-1}}}\text{ }{{\text{s}}^{\text{-1}}}}{\text{(mol }{{\text{L}}^{\text{-1}}})}\]
\[\text{= }{{\text{s}}^{\text{-1}}}\]
2. For a reaction:
$\text{2A+B }\to \text{ }{{\text{A}}_{\text{2}}}\text{B}$
The $rate=k[A]{{[B]}^{2}}$ with $\text{k = 2}\text{.0 x 1}{{\text{0}}^{\text{-6}}}\text{ mo}{{\text{l}}^{\text{-2}}}\text{ }{{\text{L}}^{\text{2}}}\text{ }{{\text{s}}^{\text{-1}}}$.
Calculate the initial rate of the reaction when $\text{ }\!\![\!\!\text{ A }\!\!]\!\!\text{ = 0}\text{.1 mol }{{\text{L}}^{\text{-1}}}$, $\text{ }\!\![\!\!\text{ B }\!\!]\!\!\text{ = 0}\text{.2 mol }{{\text{L}}^{\text{-1}}}$. Calculate the rate of reaction after [A] is reduced to $\text{0}\text{.06 mol }{{\text{L}}^{\text{-1}}}$.
Ans: We are given the rate of the reaction as:
\[rate=k[A]{{[B]}^{2}}\]
Putting the values in this, we get the rate as:
\[\text{rate = 2}\text{.0 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-6}}}\text{ }\!\!\times\!\!\text{ 0}\text{.1 }\!\!\times\!\!\text{ (0}\text{.2}{{\text{)}}^{2}}\]
\[\text{rate = 8}\text{.0 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-9}}}\text{ mol }{{\text{L}}^{-1}}\text{ }{{\text{s}}^{-1}}\]
When [A] is reduced from $0.10\text{ mol }{{\text{L}}^{-1}}$ to $0.06\text{ mol }{{\text{L}}^{-1}}$. So, the amount of [A] reacted will be:
\[=0.10-0.06=0.04\text{ mol }{{\text{L}}^{-1}}\]
Therefore, the concentration of B reacted will be:
\[=\frac{1}{2}\text{ }\!\!\times\!\!\text{ 0}\text{.04 = 0}\text{.02 mol }{{\text{L}}^{-1}}\]
Hence, new [B] = 0.2 – 0.02 = $0.18\text{ mol }{{\text{L}}^{-1}}$
Now, the new rate of the reaction will be:
\[\text{rate = 2}\text{.0 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-6}}}\text{ }\!\!\times\!\!\text{ 0}\text{.06 }\!\!\times\!\!\text{ (0}\text{.18}{{\text{)}}^{2}}\]
\[\text{rate = 3}\text{.89 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-9}}}\text{ mol }{{\text{L}}^{-1}}\text{ }{{\text{s}}^{-1}}\]
Therefore, the rate of the reaction is $\text{3}\text{.89 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-9}}}\text{ mol }{{\text{L}}^{-1}}\text{ }{{\text{s}}^{-1}}$.
3. The decomposition of $\text{N}{{\text{H}}_{\text{3}}}$ on the platinum surface is zero order reaction. What are the rates of production of ${{\text{N}}_{\text{2}}}$ and ${{\text{H}}_{\text{2}}}$ if $\text{k = 2}\text{.5 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-4}}}\text{ mo}{{\text{l}}^{\text{-1}}}\text{ L }{{\text{s}}^{\text{-1}}}$ ?
Ans: The following equation represents the breakdown of ammonia on the platinum surface.
\[\text{2N}{{\text{H}}_{{{\text{3}}_{\text{(g)}}}}}\xrightarrow{\text{Pt}}{{\text{N}}_{\text{2}}}_{_{\text{(g)}}}\text{+3}{{\text{H}}_{\text{2}}}_{_{\text{(g)}}}\]
Therefore, we can write the rate of the reaction as:
\[\text{Rate = -}\frac{\text{1}}{\text{2}}\frac{\text{d }\!\![\!\!\text{ N}{{\text{H}}_{\text{3}}}\text{ }\!\!]\!\!\text{ }}{\text{dt}}\text{ = }\frac{\text{d }\!\![\!\!\text{ }{{\text{N}}_{\text{2}}}\text{ }\!\!]\!\!\text{ }}{\text{dt}}\text{ = }\frac{\text{1}}{\text{3}}\frac{\text{d }\!\![\!\!\text{ }{{\text{H}}_{\text{2}}}\text{ }\!\!]\!\!\text{ }}{\text{dt}}\]
But we are given that the reaction is a zero order reaction.
So, \[\text{Rate = -}\frac{\text{1}}{\text{2}}\frac{\text{d }\!\![\!\!\text{ N}{{\text{H}}_{\text{3}}}\text{ }\!\!]\!\!\text{ }}{\text{dt}}\text{ = }\frac{\text{d }\!\![\!\!\text{ }{{\text{N}}_{\text{2}}}\text{ }\!\!]\!\!\text{ }}{\text{dt}}\text{ = }\frac{\text{1}}{\text{3}}\frac{\text{d }\!\![\!\!\text{ }{{\text{H}}_{\text{2}}}\text{ }\!\!]\!\!\text{ }}{\text{dt}}\text{ = 2}\text{.5 }\!\!\times\!\!\text{ 1}{{\text{0}}^{-4}}\text{ mol }{{\text{L}}^{-1}}\text{ }{{\text{s}}^{-1}}\]
Thus, the rate of production of ${{\text{N}}_{\text{2}}}$ will be:
\[\text{ }\frac{\text{d }\!\![\!\!\text{ }{{\text{N}}_{\text{2}}}\text{ }\!\!]\!\!\text{ }}{\text{dt}}\text{ = 2}\text{.5 }\!\!\times\!\!\text{ 1}{{\text{0}}^{-4}}\text{ mol }{{\text{L}}^{-1}}\text{ }{{\text{s}}^{-1}}\]
And the rate of production of ${{\text{H}}_{\text{2}}}$ will be:
\[\frac{\text{d }\!\![\!\!\text{ }{{\text{H}}_{\text{2}}}\text{ }\!\!]\!\!\text{ }}{\text{dt}}\text{ = 3 }\!\!\times\!\!\text{ 2}\text{.5 }\!\!\times\!\!\text{ 1}{{\text{0}}^{-4}}\text{ mol }{{\text{L}}^{-1}}\text{ }{{\text{s}}^{-1}}=7.\text{5 }\!\!\times\!\!\text{ 1}{{\text{0}}^{-4}}\text{ mol }{{\text{L}}^{-1}}\text{ }{{\text{s}}^{-1}}\]
4. The decomposition of dimethyl ether leads to the formation of $\text{C}{{\text{H}}_{\text{4}}}$, ${{\text{H}}_{\text{2}}}$ and CO and the reaction rate is given by $\text{Rate = k }\!\![\!\!\text{ C}{{\text{H}}_{\text{3}}}\text{OC}{{\text{H}}_{\text{3}}}{{\text{ }\!\!]\!\!\text{ }}^{\text{3/2}}}$
The rate of reaction is followed by increase in pressure in a closed vessel, so the rate can also be expressed in terms of the partial pressure of dimethyl ether, i.e.,
$\text{Rate = k (}{{\text{P}}_{\text{C}{{\text{H}}_{\text{3}}}\text{OC}{{\text{H}}_{\text{3}}}}}{{\text{)}}^{\text{3/2}}}$
If the pressure is measured in bar and time in minutes, then what are the units of rate and rate constants?
Ans: If the pressure is measured in bar and time in minutes, then unit of rate will be:
\[\text{= bar mi}{{\text{n}}^{\text{-1}}}\]
We are given the rate of the reaction as: $\text{Rate = k }\!\![\!\!\text{ C}{{\text{H}}_{\text{3}}}\text{OC}{{\text{H}}_{\text{3}}}{{\text{ }\!\!]\!\!\text{ }}^{\text{3/2}}}$
Therefore, $\text{k = }\frac{\text{Rate}}{\text{ }\!\![\!\!\text{ C}{{\text{H}}_{\text{3}}}\text{OC}{{\text{H}}_{\text{3}}}{{\text{ }\!\!]\!\!\text{ }}^{\text{3/2}}}}$
So, we can write the units of rate constant as:
\[\text{k = }\frac{\text{bar mi}{{\text{n}}^{\text{-1}}}}{\text{ba}{{\text{r}}^{\text{3/2}}}}\text{ = ba}{{\text{r}}^{\text{-1/2}}}\text{ mi}{{\text{n}}^{\text{-1}}}\]
So, the units are \[\text{ba}{{\text{r}}^{\text{-1/2}}}\text{ mi}{{\text{n}}^{\text{-1}}}\]
6. Mention the factors that affect the rate of a chemical reaction.
Ans: Factors that influence a reaction's speed include.
Reactant nature: The rate of reaction is affected by the kind of reactant. For example, ionic compound reactions are quicker than covalent compound reactions.
The state of the reactants: Solid reactions are sluggish, liquid reactions are rapid, and gas reactions are very quick.
Temperature: In addition, temperature has a significant impact on response rate. Every 10 degrees Celsius increase in temperature doubles the pace of reaction.
Presence of catalyst: The rate of reaction is also affected by the presence of a catalyst in the reaction. It enhances the pace of reaction by increasing reaction surface area, by generating unstable intermediates with the substrate, and by offering a lower activation energy alternative path.
7. A reaction is second order with respect to a reactant. How is the rate of reaction affected if the concentration of the reactant is:
(i). Doubled
Ans: Let us assume that the concentration of the reactant be [A] = a
Rate of the reaction will be:
\[\text{R = k }\!\![\!\!\text{ A}{{\text{ }\!\!]\!\!\text{ }}^{\text{2}}}\text{ = k}{{\text{a}}^{\text{2}}}\]
It is said that the concentration of A increases by two times, so we can write:
[A] = 2a mol/ L
Therefore, the rate of reaction will be:
\[\text{Rate = k (2a}{{\text{)}}^{\text{2}}}\text{ = 4 k}{{\text{a}}^{\text{2}}}\]
Thus, the rate of the reaction will increase by 4 times.
(ii). Reduced to half
It is said that the concentration of A reduced to half, so we can write:
[X] = $\frac{1}{2}$ a mol/ L
Therefore, the rate of reaction will be:
\[\text{Rate = k }{{\left[ \frac{1}{2}a \right]}^{2}}\text{ = }\frac{1}{4}\text{ k}{{\text{a}}^{\text{2}}}\]
Thus, the rate of the reaction will reduce by ¼ times.
8. What is the effect of temperature on the rate constant of a reaction? How can this temperature effect on rate constant be represented quantitatively?
Ans: An increase of 10 degrees in temperature causes a reaction's rate constant to almost double in size. In any case, the Arrhenius equation gives the exact temperature dependency of a chemical reaction rate.
The Arrhenius equation is given below:
\[\text{k = A }{{\text{e}}^{\text{-}{{\text{E}}_{\text{a}}}\text{/Rt}}}\]
Where, A is the Arrhenius factor or the frequency factor,
T is the temperature,
R is the gas constant,
${{\text{E}}_{\text{a}}}$ is the activation energy.
The formula can also be written as:
\[\text{log}\frac{{{\text{k}}_{\text{2}}}}{{{\text{k}}_{\text{1}}}}\text{ = }\frac{{{\text{E}}_{\text{a}}}}{\text{2}\text{.303R}}\left[ \frac{{{\text{T}}_{\text{2}}}\text{-}{{\text{T}}_{\text{1}}}}{{{\text{T}}_{\text{1}}}{{\text{T}}_{\text{2}}}} \right]\]
Where ${{\text{k}}_{\text{2}}}$is the rate constant at temperature \[{{\text{T}}_{\text{2}}}\]
${{\text{k}}_{1}}$ is the rate constant at temperature ${{\text{T}}_{\text{1}}}$
9. In a pseudo first order hydrolysis of ester in water, the following results were obtained
t/s | 0 | 30 | 60 | 90 |
$\text{ }\!\![\!\!\text{ Ester }\!\!]\!\!\text{ mol }{{\text{L}}^{\text{-1}}}$ | 0.55 | 0.31 | 0.17 | 0.085 |
(i). Calculate the average rate of reaction between the time interval 30 to 60 seconds.
Ans: Between the time interval of 30 to 60 sec the average rate of reaction will be calculated as:
\[\text{= }\frac{\text{d }\!\![\!\!\text{ Ester }\!\!]\!\!\text{ }}{\text{dt}}\]
Putting the values from the data given in the question, we can write:
\[\text{= }\frac{0.31-0.17}{60-30}=\frac{0.14}{30}\]
\[\text{= 4}\text{.67 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-3}}}\text{ mol }{{\text{L}}^{\text{-1}}}\text{ }{{\text{s}}^{\text{-1}}}\]
(ii). Calculate the pseudo first order rate constant for the hydrolysis of ester.
Ans: The rate law formula for pseudo first order reaction will be:
\[\text{k = }\frac{\text{2}\text{.303}}{\text{t}}\text{ log}\frac{{{\text{ }\!\![\!\!\text{ R }\!\!]\!\!\text{ }}_{\text{0}}}}{\text{ }\!\![\!\!\text{ R }\!\!]\!\!\text{ }}\]
Now, when t = 30 s, then we rate constant will be:
\[{{\text{k}}_{1}}\text{ = }\frac{\text{2}\text{.303}}{30}\text{ log}\frac{0.55}{0.31}=1.91\text{ }\!\!\times\!\!\text{ 1}{{\text{0}}^{-2}}\text{ }{{\text{s}}^{-1}}\]
Now, when t = 60 s, then we rate constant will be:
\[{{\text{k}}_{2}}\text{ = }\frac{\text{2}\text{.303}}{60}\text{ log}\frac{0.55}{0.17}=1.96\text{ }\!\!\times\!\!\text{ 1}{{\text{0}}^{-2}}\text{ }{{\text{s}}^{-1}}\]
Now, when t = 90 s, then we rate constant will be:
\[{{\text{k}}_{3}}\text{ = }\frac{\text{2}\text{.303}}{90}\text{ log}\frac{0.55}{0.085}=2.075\text{ }\!\!\times\!\!\text{ 1}{{\text{0}}^{-2}}\text{ }{{\text{s}}^{-1}}\]
So, we can calculate the average rate constant as:
\[\text{k = }\frac{{{\text{k}}_{\text{1}}}\text{ + }{{\text{k}}_{\text{2}}}\text{ + }{{\text{k}}_{\text{3}}}}{\text{3}}\]
\[\text{=1}\text{.98 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-2}}}\text{ }{{\text{s}}^{\text{-1}}}\]
10. A reaction is first order in A and second order in B.
(i). Write the differential rate equation
Ans: The differential rate equation can be written as:
\[\text{-}\frac{\text{d }\!\![\!\!\text{ R }\!\!]\!\!\text{ }}{\text{dt}}\text{ = k }\!\![\!\!\text{ A }\!\!]\!\!\text{ }\!\![\!\!\text{ B}{{\text{ }\!\!]\!\!\text{ }}^{\text{2}}}\]
(ii). How is the rate affected by increasing the concentration of B three times?
Ans: The concentration of B is increased by 3 times, then B =3B
Therefore, the rate will be:
\[\text{-}\frac{\text{d }\!\![\!\!\text{ R }\!\!]\!\!\text{ }}{\text{dt}}\text{ = k }\!\![\!\!\text{ A }\!\!]\!\!\text{ }\!\![\!\!\text{ 3B}{{\text{ }\!\!]\!\!\text{ }}^{\text{2}}}=9\text{ }\times \text{ }\!\![\!\!\text{ A }\!\!]\!\!\text{ }\!\![\!\!\text{ B}{{\text{ }\!\!]\!\!\text{ }}^{\text{2}}}\]
Therefore, the rate will increase by 9 times.
(iii). How is the rate affected when the concentration of both A and B are doubled?
Ans: The concentration of A is doubled, then A = 2A
The concentration of B is doubled, then B = 2B
Therefore, the rate will be:
\[\text{-}\frac{\text{d }\!\![\!\!\text{ R }\!\!]\!\!\text{ }}{\text{dt}}\text{ = k }\!\![\!\!\text{ 2A }\!\!]\!\!\text{ }\!\![\!\!\text{ 2B}{{\text{ }\!\!]\!\!\text{ }}^{\text{2}}}=8\text{ }\times \text{ }\!\![\!\!\text{ A }\!\!]\!\!\text{ }\!\![\!\!\text{ B}{{\text{ }\!\!]\!\!\text{ }}^{\text{2}}}\]
Therefore, the rate will increase by 8 times.
11. In a reaction between A and B the initial rate of reaction $\text{(}{{\text{r}}_{\text{0}}}\text{)}$ was measured for different concentrations of A and B as given below:
$\text{A/mol }{{\text{L}}^{\text{-1}}}$ | 0.20 | 0.20 | 0.04 |
$\text{B/mol }{{\text{L}}^{\text{-1}}}$ | 0.30 | 0.10 | 0.05 |
${{\text{r}}_{\text{0}}}\text{/mol }{{\text{L}}^{\text{-1}}}\text{ }{{\text{s}}^{\text{-1}}}$ | $\text{5}\text{.07 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-5}}}$ | $\text{5}\text{.07 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-5}}}$ | $\text{1}\text{.43 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-4}}}$ |
What is the order of the reaction with respect to A and B?
Ans: Let us assume that the order of the reaction with respect to A be x and with respect to B be y.
Therefore, we can write:
\[{{\text{r}}_{\text{0}}}\text{ = k }\!\![\!\!\text{ A}{{\text{ }\!\!]\!\!\text{ }}^{\text{x}}}\text{ }\!\![\!\!\text{ B}{{\text{ }\!\!]\!\!\text{ }}^{\text{y}}}\]
\[\text{5}\text{.07 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-5}}}\text{ = k }\!\![\!\!\text{ 0}\text{.20}{{\text{ }\!\!]\!\!\text{ }}^{\text{x}}}\text{ }\!\![\!\!\text{ 0}\text{.30}{{\text{ }\!\!]\!\!\text{ }}^{\text{y}}}\text{ }.........(i)\]
\[\text{5}\text{.07 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-5}}}\text{ = k }\!\![\!\!\text{ 0}\text{.20}{{\text{ }\!\!]\!\!\text{ }}^{\text{x}}}\text{ }\!\![\!\!\text{ 0}\text{.10}{{\text{ }\!\!]\!\!\text{ }}^{\text{y}}}\text{ }.........(ii)\]
\[\text{1}\text{.43 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-5}}}\text{ = k }\!\![\!\!\text{ 0}\text{.40}{{\text{ }\!\!]\!\!\text{ }}^{\text{x}}}\text{ }\!\![\!\!\text{ 0}\text{.05}{{\text{ }\!\!]\!\!\text{ }}^{\text{y}}}\text{ }.........(iii)\]
Let us divide (i) by (ii), we get:
\[\frac{\text{5}\text{.07 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-5}}}}{\text{5}\text{.07 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-5}}}\text{ }}\text{ = }\frac{\text{k }\!\![\!\!\text{ 0}\text{.20}{{\text{ }\!\!]\!\!\text{ }}^{\text{x}}}\text{ }\!\![\!\!\text{ 0}\text{.30}{{\text{ }\!\!]\!\!\text{ }}^{\text{y}}}}{\text{ k }\!\![\!\!\text{ 0}\text{.20}{{\text{ }\!\!]\!\!\text{ }}^{\text{x}}}\text{ }\!\![\!\!\text{ 0}\text{.10}{{\text{ }\!\!]\!\!\text{ }}^{\text{y}}}}\text{ }\]
\[\text{=1 = }\frac{{{\text{ }\!\![\!\!\text{ 0}\text{.30 }\!\!]\!\!\text{ }}^{\text{y}}}}{{{\text{ }\!\![\!\!\text{ 0}\text{.10 }\!\!]\!\!\text{ }}^{\text{y}}}}\]
\[\text{= }{{\left( \frac{\text{0}\text{.30}}{\text{0}\text{.10}} \right)}^{\text{x}}}\text{ = }{{\left( \frac{\text{0}\text{.30}}{\text{0}\text{.10}} \right)}^{\text{y}}}\]
Therefore, y = 0
Now, dividing (iii) by (i), we get:
\[\frac{\text{1}\text{.43 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-4}}}}{\text{5}\text{.07 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-5}}}\text{ }}\text{ = }\frac{\text{k }\!\![\!\!\text{ 0}\text{.40}{{\text{ }\!\!]\!\!\text{ }}^{\text{x}}}\text{ }\!\![\!\!\text{ 0}\text{.05}{{\text{ }\!\!]\!\!\text{ }}^{\text{y}}}}{\text{ k }\!\![\!\!\text{ 0}\text{.20}{{\text{ }\!\!]\!\!\text{ }}^{\text{x}}}\text{ }\!\![\!\!\text{ 0}\text{.30}{{\text{ }\!\!]\!\!\text{ }}^{\text{y}}}}\text{ }\]
\[\frac{\text{1}\text{.43 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-4}}}}{\text{5}\text{.07 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-5}}}\text{ }}\text{ = }\frac{\text{k }\!\![\!\!\text{ 0}\text{.40}{{\text{ }\!\!]\!\!\text{ }}^{\text{x}}}\text{ }}{\text{ k }\!\![\!\!\text{ 0}\text{.20}{{\text{ }\!\!]\!\!\text{ }}^{\text{x}}}\text{ }}\]
Because y = 0
\[\text{= 2}\text{.821 = }{{\text{2}}^{\text{x}}}\]
Now, taking log on both sides.
log 2.821 = x log 2
\[\text{x = }\frac{\text{log 2}\text{.821}}{\text{log 2}}\]
x = 1.496
x = 1.5
Thus, the order of the reaction according to A is 1.5 and according to B is 0.
12. The following results have been obtained during the kinetic studies of the reaction.
\[\text{2A + B}\to \text{ C + D}\]
Experiment | $\text{A/mol }{{\text{L}}^{\text{-1}}}$ | $\text{B/mol }{{\text{L}}^{\text{-1}}}$ | Initial rate of formation of $\text{D/mol }{{\text{L}}^{\text{-1}}}\text{mi}{{\text{n}}^{\text{-1}}}$ |
I | 0.1 | 0.1 | $\text{6}\text{.0 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-3}}}$ |
II | 0.3 | 0.2 | $\text{7}\text{.3 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-2}}}$ |
III | 0.3 | 0.4 | $\text{2}\text{.88 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-1}}}$ |
IV | 0.4 | 0.1 | $\text{2}\text{.40 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-2}}}$ |
Determine the rate law and the rate constant for the reaction.
Ans: Let us assume that the order of the reaction with respect to A be x and with respect to B be y.
Therefore, we can write:
\[\text{Rate = k }\!\![\!\!\text{ A}{{\text{ }\!\!]\!\!\text{ }}^{\text{x}}}\text{ }\!\![\!\!\text{ B}{{\text{ }\!\!]\!\!\text{ }}^{\text{y}}}\]
\[\text{6}\text{.0 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-3}}}\text{ = k }\!\![\!\!\text{ 0}\text{.1}{{\text{ }\!\!]\!\!\text{ }}^{\text{x}}}\text{ }\!\![\!\!\text{ 0}\text{.1}{{\text{ }\!\!]\!\!\text{ }}^{\text{y}}}\text{ }.........(i)\]
\[\text{7}\text{.2 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-2}}}\text{ = k }\!\![\!\!\text{ 0}\text{.3}{{\text{ }\!\!]\!\!\text{ }}^{\text{x}}}\text{ }\!\![\!\!\text{ 0}\text{.2}{{\text{ }\!\!]\!\!\text{ }}^{\text{y}}}\text{ }.........(ii)\]
\[\text{2}\text{.88 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-1}}}\text{ = k }\!\!~\!\!\text{ }\!\![\!\!\text{ 0}\text{.3}{{\text{ }\!\!]\!\!\text{ }}^{\text{x}}}\text{ }\!\!~\!\!\text{ }\!\![\!\!\text{ 0}\text{.1}{{\text{ }\!\!]\!\!\text{ }}^{\text{y}}}\text{ }\!\!~\!\!\text{ }\!\!~\!\!\text{ }.........\text{(iii)}\]
\[\text{2}\text{.40 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-2}}}\text{ = k }\!\![\!\!\text{ 0}\text{.4}{{\text{ }\!\!]\!\!\text{ }}^{\text{x}}}\text{ }\!\![\!\!\text{ 0}\text{.1}{{\text{ }\!\!]\!\!\text{ }}^{\text{y}}}\text{ }.........(iv) \]
Let us divide (iv) by (i), we get:
\[\frac{\text{2}\text{.40 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-2}}}}{\text{6}\text{.0 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-3}}}\text{ }}\text{ = }\frac{\text{k }\!\![\!\!\text{ 0}\text{.4}{{\text{ }\!\!]\!\!\text{ }}^{\text{x}}}\text{ }\!\![\!\!\text{ 0}\text{.1}{{\text{ }\!\!]\!\!\text{ }}^{\text{y}}}}{\text{ k }\!\![\!\!\text{ 0}\text{.1}{{\text{ }\!\!]\!\!\text{ }}^{\text{x}}}\text{ }\!\![\!\!\text{ 0}\text{.1}{{\text{ }\!\!]\!\!\text{ }}^{\text{y}}}}\text{ }\]
\[\text{=4 = }\frac{{{\text{ }\!\![\!\!\text{ 0}\text{.4 }\!\!]\!\!\text{ }}^{x}}}{{{\text{ }\!\![\!\!\text{ 0}\text{.1 }\!\!]\!\!\text{ }}^{x}}}\]
\[\text{= 4 = }{{\left( \frac{\text{0}\text{.4}}{\text{0}\text{.1}} \right)}^{x}}\]
Therefore, x = 1
Now, dividing (iii) by (ii), we get:
\[\frac{\text{2}\text{.88 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-1}}}}{\text{7}\text{.2 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-2}}}\text{ }}\text{ = }\frac{\text{k }\!\![\!\!\text{ 0}\text{.3}{{\text{ }\!\!]\!\!\text{ }}^{\text{x}}}\text{ }\!\![\!\!\text{ 0}\text{.4}{{\text{ }\!\!]\!\!\text{ }}^{\text{y}}}}{\text{ k }\!\![\!\!\text{ 0}\text{.3}{{\text{ }\!\!]\!\!\text{ }}^{\text{x}}}\text{ }\!\![\!\!\text{ 0}\text{.2}{{\text{ }\!\!]\!\!\text{ }}^{\text{y}}}}\text{ }\]
\[\text{= 4 = }{{\left( \frac{\text{0}\text{.4}}{\text{0}\text{.2}} \right)}^{y}}\]
\[\text{= 4 = }{{\text{2}}^{\text{y}}}\]
\[\text{= }{{\text{2}}^{2}}\text{ = }{{\text{2}}^{\text{y}}}\]
y = 2
Thus, the order of the reaction according to A is 1 and according to B is 2.
So, the rate law is:
\[\text{Rate = k }\!\![\!\!\text{ A }\!\!]\!\!\text{ }\!\![\!\!\text{ B}{{\text{ }\!\!]\!\!\text{ }}^{\text{2}}}\]
\[\text{k = }\frac{\text{Rate}}{\text{ }\!\![\!\!\text{ A }\!\!]\!\!\text{ }\!\![\!\!\text{ B}{{\text{ }\!\!]\!\!\text{ }}^{\text{2}}}}\]
Now, putting the values for each experiment, we get:
From experiment I:
\[\text{k = }\frac{6.0\text{ }\!\!\times\!\!\text{ 1}{{\text{0}}^{-3}}}{\text{ }\!\![\!\!\text{ 0}\text{.1 }\!\!]\!\!\text{ }\!\![\!\!\text{ 0}\text{.1}{{\text{ }\!\!]\!\!\text{ }}^{\text{2}}}}\]
\[\text{= 6}\text{.0 }{{\text{L}}^{\text{2}}}\text{ mo}{{\text{l}}^{\text{-2}}}\text{ mi}{{\text{n}}^{\text{-1}}}\]
From experiment II:
\[\text{k = }\frac{\text{7}\text{.3 }\!\!\times\!\!\text{ 1}{{\text{0}}^{-2}}}{\text{ }\!\![\!\!\text{ 0}\text{.3 }\!\!]\!\!\text{ }\!\![\!\!\text{ 0}\text{.2}{{\text{ }\!\!]\!\!\text{ }}^{\text{2}}}}\]
\[\text{= 6}\text{.0 }{{\text{L}}^{\text{2}}}\text{ mo}{{\text{l}}^{\text{-2}}}\text{ mi}{{\text{n}}^{\text{-1}}}\]
From experiment III:
\[\text{k = }\frac{\text{2}\text{.88 }\!\!\times\!\!\text{ 1}{{\text{0}}^{-1}}}{\text{ }\!\![\!\!\text{ 0}\text{.3 }\!\!]\!\!\text{ }\!\![\!\!\text{ 0}\text{.4}{{\text{ }\!\!]\!\!\text{ }}^{\text{2}}}}\]
\[\text{= 6}\text{.0 }{{\text{L}}^{\text{2}}}\text{ mo}{{\text{l}}^{\text{-2}}}\text{ mi}{{\text{n}}^{\text{-1}}}\]
From experiment IV:
\[\text{k = }\frac{\text{2}\text{.40 }\!\!\times\!\!\text{ 1}{{\text{0}}^{-2}}}{\text{ }\!\![\!\!\text{ 0}\text{.4 }\!\!]\!\!\text{ }\!\![\!\!\text{ 0}\text{.1}{{\text{ }\!\!]\!\!\text{ }}^{\text{2}}}}\]
\[\text{= 6}\text{.0 }{{\text{L}}^{\text{2}}}\text{ mo}{{\text{l}}^{\text{-2}}}\text{ mi}{{\text{n}}^{\text{-1}}}\]
Therefore, the rate constant will be k $\text{= 6}\text{.0 }{{\text{L}}^{\text{2}}}\text{ mo}{{\text{l}}^{\text{-2}}}\text{ mi}{{\text{n}}^{\text{-1}}}$
13. The reaction between A and B is first order with respect to A and zero order with respect to B. Fill in the blanks in the following table:
Experiment | $\text{A/mol }{{\text{L}}^{\text{-1}}}$ | $\text{B/mol }{{\text{L}}^{\text{-1}}}$ | Initial rate $\text{D/mol }{{\text{L}}^{\text{-1}}}\text{mi}{{\text{n}}^{\text{-1}}}$ |
I | 0.1 | 0.1 | $\text{2}\text{.0 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-2}}}$ |
II | --- | 0.2 | $\text{4}\text{.0 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-2}}}$ |
III | 0.4 | 0.4 | ---- |
IV | ---- | 0.2 | $\text{2}\text{.0 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-2}}}$ |
Ans: We are given that, the reaction between A and B is first order with respect to A and zero order with respect to B.
Therefore, the rate of the reaction is given by:
\[\text{Rate = k }\!\![\!\!\text{ A}{{\text{ }\!\!]\!\!\text{ }}^{\text{1}}}{{\text{ }\!\![\!\!\text{ B }\!\!]\!\!\text{ }}^{\text{0}}}\]
So, we can write:
\[\text{Rate = k }\!\![\!\!\text{ A }\!\!]\!\!\text{ }\]
According to the experiment I we can write:
\[\text{2}\text{.0 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-2}}}\text{ = k(0}\text{.1)}\]
\[\text{k = 0}\text{.2 mi}{{\text{n}}^{\text{-1}}}\]
According to the experiment II we can write:
\[4.0\text{ }\!\!\times\!\!\text{ 1}{{\text{0}}^{-2}}=(0.2)\text{ }\!\![\!\!\text{ A }\!\!]\!\!\text{ }\]
\[\text{ }\!\![\!\!\text{ A }\!\!]\!\!\text{ = 0}\text{.2 mol }{{\text{L}}^{\text{-1}}}\]
According to the experiment III we can write:
\[\text{Rate = 0}\text{.2 }\!\!\times\!\!\text{ 0}\text{.4}\]
\[\text{= 0}\text{.08 mol }{{\text{L}}^{\text{-1}}}\text{ mi}{{\text{n}}^{\text{-1}}}\]
According to the experiment III we can write:
\[2.0\text{ }\!\!\times\!\!\text{ 1}{{\text{0}}^{-2}}=(0.2)\text{ }\!\![\!\!\text{ A }\!\!]\!\!\text{ }\]
\[\text{ }\!\![\!\!\text{ A }\!\!]\!\!\text{ = 0}\text{.1 mol }{{\text{L}}^{\text{-1}}}\]
14. Calculate the half-life of a first order reaction from their rate constants given below:
(i). $\text{200 }{{\text{s}}^{\text{-1}}}$
Ans: Half-life of the reaction can be related with the rate constant of the reaction as:
\[{{\text{t}}_{\text{1/2}}}\text{ = }\frac{\text{0}\text{.693}}{\text{k}}\]
Putting the value of time, we get:
\[\text{k = }\frac{\text{0}\text{.693}}{\text{200}}\text{ = 3}\text{.46 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-3}}}\text{ s}\]
So, the rate of the reaction is $\text{3}\text{.46 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-3}}}\text{ s}$
(ii). $\text{2 mi}{{\text{n}}^{\text{-1}}}$
Ans: Half-life of the reaction can be related with the rate constant of the reaction as:
\[{{\text{t}}_{\text{1/2}}}\text{ = }\frac{\text{0}\text{.693}}{\text{k}}\]
Putting the value of time, we get:
\[\text{k = }\frac{\text{0}\text{.693}}{\text{2}}\text{ = 0}\text{.346 min}\]
So, the rate of the reaction is 0.346 min.
(iii). $\text{4 year}{{\text{s}}^{\text{-1}}}$
Ans: Half-life of the reaction can be related with the rate constant of the reaction as:
\[{{\text{t}}_{\text{1/2}}}\text{ = }\frac{\text{0}\text{.693}}{\text{k}}\]
Putting the value of time, we get:
\[\text{k = }\frac{\text{0}\text{.693}}{4}\text{ = 0}\text{.173 years}\]
So, the rate of the reaction is 0.173 years.
15. The half-life for radioactive decay of $^{\text{14}}\text{C}$ is 5730 years. An archeological artifact containing wood had only 80% of the $^{\text{14}}\text{C}$ found in a living tree. Estimate the age of the sample.
Ans: The given reaction in the above question is radioactive decay and the radioactive decay follows the first order kinetics. Therefore, the decay constant:
\[\text{ }\!\!\lambda\!\!\text{ = }\frac{\text{0}\text{.693}}{{{\text{t}}_{\text{1/2}}}}\]
We are given a half-life of 5730 years.
\[\text{ }\!\!\lambda\!\!\text{ = }\frac{\text{0}\text{.693}}{5730}\text{ year}{{\text{s}}^{-1}}\]
To find the age of the sample, we can write:
\[\text{t = }\frac{\text{2}\text{.303}}{\text{ }\!\!\lambda\!\!\text{ }}\text{ log}\frac{{{\text{ }\!\![\!\!\text{ R }\!\!]\!\!\text{ }}_{\text{0}}}}{\text{ }\!\![\!\!\text{ R }\!\!]\!\!\text{ }}\]
80% of the wood is found so, the initial amount can be taken as 100 and the final amount as 80. Putting the values, we get:
\[\text{t = }\frac{\text{2}\text{.303}}{\frac{0.693}{5730}}\text{ log}\frac{100}{80}\]
t = 1845 years
Therefore, the age of the sample is 1845 years.
16. The experiment data for decomposition of ${{\text{N}}_{\text{2}}}{{\text{O}}_{\text{5}}}$
\[\text{ }\!\![\!\!\text{ 2}{{\text{N}}_{\text{2}}}{{\text{O}}_{\text{5}}}\to \text{4N}{{\text{O}}_{\text{2}}}\text{+}{{\text{O}}_{\text{2}}}\text{ }\!\!]\!\!\text{ }\]
In gas phase at 318 K are given below:
t/s | 0 | 400 | 800 | 1200 | 1600 | 2000 | 2400 | 1800 | 3200 |
$\text{1}{{\text{0}}^{\text{-2}}}\text{ }\!\!\times\!\!\text{ }\!\![\!\!\text{ }{{\text{N}}_{\text{2}}}{{\text{O}}_{\text{5}}}\text{ }\!\!]\!\!\text{ /mol }{{\text{L}}^{\text{-1}}}$ | 1.63 | 1.36 | 1.14 | 0.93 | 0.78 | 0.64 | 0.53 | 0.43 | 0.35 |
(i). Plot [${{\text{N}}_{\text{2}}}{{\text{O}}_{\text{5}}}$] against t
Ans: The graph is given below:
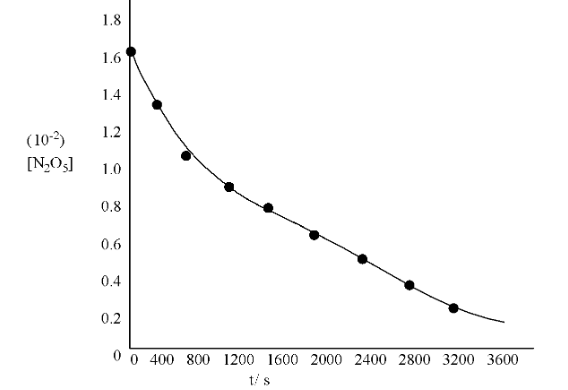
(ii). Find the half-life period for the reaction
Ans: Time corresponding to the concentration,
$\frac{\text{1}\text{.630 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-2}}}}{\text{2}}\text{ mol }{{\text{L}}^{\text{-1}}}\text{=0}\text{.815 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-2}}}\text{ mol }{{\text{L}}^{\text{-1}}}$ is the half-life.
From the graph, the half life obtained is 1440 s.
(iii). Draw the graph between $\text{log }\!\![\!\!\text{ }{{\text{N}}_{\text{2}}}{{\text{O}}_{\text{5}}}\text{ }\!\!]\!\!\text{ }$ and t
Ans:
T(s) | $\text{1}{{\text{0}}^{\text{-2}}}\text{ }\!\!\times\!\!\text{ }\!\![\!\!\text{ }{{\text{N}}_{\text{2}}}{{\text{O}}_{\text{5}}}\text{ }\!\!]\!\!\text{ /mol }{{\text{L}}^{\text{-1}}}$ | $\text{log }\!\![\!\!\text{ }{{\text{N}}_{\text{2}}}{{\text{O}}_{\text{5}}}\text{ }\!\!]\!\!\text{ }$ |
0 | 1.63 | -1.79 |
400 | 1.36 | -1.87 |
800 | 1.14 | -1.94 |
1200 | 0.93 | -2.03 |
1600 | 0.78 | -2.11 |
2000 | 0.64 | -2.19 |
2400 | 0.53 | -2.28 |
2800 | 0.43 | -2.37 |
3200 | 0.35 | -2.46 |
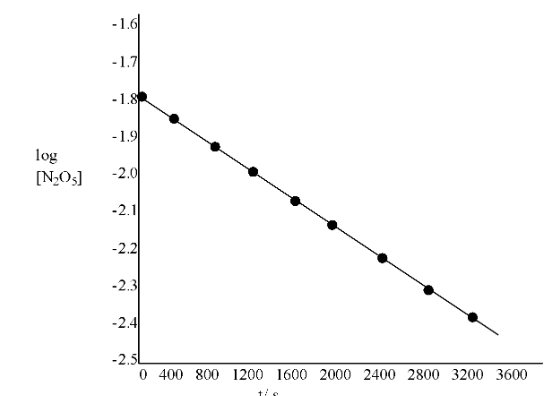
(iv). What is the rate law?
Ans: The rate law of the reaction will be:
\[\text{Rate = k }\!\![\!\!\text{ }{{\text{N}}_{\text{2}}}{{\text{O}}_{\text{5}}}\text{ }\!\!]\!\!\text{ }\]
(v). Calculate the rate constant.
Ans: From the plot $\text{ }\!\![\!\!\text{ }{{\text{N}}_{\text{2}}}{{\text{O}}_{\text{5}}}\text{ }\!\!]\!\!\text{ }$ v/s t, is given by:
\[\text{= -}\frac{\text{k}}{\text{2}\text{.303}}\]
Therefore, we obtain:
\[\text{= -}\frac{\text{k}}{\text{2}\text{.303}}=\frac{0.67}{3200}\]
\[\text{= 4}\text{.82 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-4}}}\text{ mol }{{\text{L}}^{\text{-1}}}\text{ }{{\text{s}}^{\text{-1}}}\]
(vi). Calculate the half-life period from k and compare it will (ii)
Ans: Half-life is given by:
\[{{t}_{1/2}}=\frac{0.693}{k}=\frac{0.693}{4.82\text{ }\!\!\times\!\!\text{ 1}{{\text{0}}^{-4}}}s\]
= 1438 seconds.
The value of half-life calculated from the k is very close to that obtained from the graph.
16. The rate constant for a first order reaction is $\text{60 }{{\text{s}}^{\text{-1}}}$ . How much time will it take to reduce the initial concentration of the reactant to its 1/16th value?
Ans: As we know that:
\[\text{t = }\frac{\text{2}\text{.303}}{\text{k}}\text{ log}\frac{{{\text{ }\!\![\!\!\text{ R }\!\!]\!\!\text{ }}_{\text{0}}}}{\text{ }\!\![\!\!\text{ R }\!\!]\!\!\text{ }}\]
The initial value of the reactant has become 1/16th. Now, putting the values, we get:
\[\text{t = }\frac{\text{2}\text{.303}}{60}\text{ log}\frac{16}{1}\]
\[\text{t = }\frac{\text{2}\text{.303}}{\text{60}}\text{ log16 = 4}\text{.62 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-2}}}\text{ s}\]
Therefore, the time required will be $4.62\text{ }\!\!\times\!\!\text{ 1}{{\text{0}}^{-2}}\text{ s}$.
17. During a nuclear explosion, one of the products is $^{\text{90}}\text{Sr}$ with a half-life of 28.1 years. If 1 $\text{ }\!\!\mu\!\!\text{ g}$ of $^{\text{90}}\text{Sr}$ was absorbed in the bones of a newly born baby instead of calcium, how much of it will remain after 10 years and 60 years if it is not lost metabolically.
Ans: As radioactive disintegration follows first order kinetics.
Decay constant of $^{\text{90}}\text{Sr}$ (k) = $\frac{0.693}{{{t}_{1/2}}}=\frac{0.693}{28.1}=2.466\text{ }\!\!\times\!\!\text{ 1}{{\text{0}}^{-2}}\text{ }{{\text{y}}^{-1}}$
To calculate the amount left after 10 years.
\[\text{a = 1 }\!\!\mu\!\!\text{ g}\]
$t = 10 years$
\[\text{k=2}\text{.466 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-2}}}\text{ }{{\text{y}}^{\text{-1}}}\]
$(a-x) = ?$
\[\text{k = }\frac{\text{2}\text{.303}}{\text{t}}\text{ log}\frac{\text{a}}{\text{a-x}}\]
\[\text{2}\text{.466 }\!\!\times\!\!\text{ 1}{{\text{0}}^{-2}}\text{ = }\frac{\text{2}\text{.303}}{10}\text{ log}\frac{1}{\text{a-x}}\]
\[\text{log(a-x) = -0}\text{.1071}\]
(a-x) = Antilog -0.1071 = 0.7814 \[\text{ }\!\!\mu\!\!\text{ g}\]
To calculate the amount left after 60 years.
\[\text{k = }\frac{\text{2}\text{.303}}{\text{t}}\text{ log}\frac{\text{a}}{\text{a-x}}\]
\[\text{2}\text{.466 }\!\!\times\!\!\text{ 1}{{\text{0}}^{-2}}\text{ = }\frac{\text{2}\text{.303}}{60}\text{ log}\frac{1}{\text{a-x}}\]
\[\text{log(a-x) = -0}\text{.6425}\]
(a-x) = Antilog -0.6425 = 0.2278 $\text{ }\!\!\mu\!\!\text{ g}$
18. For a first order reaction, show that time required for 99% completion is twice the time required for the completion of 90% of reaction.
Ans: For first order reaction, we can write:
\[{{t}_{99\text{ % } \!\!\!\!\text{ }}}=\frac{2.303}{k}\log \frac{a}{a-x}\]
99% completion means that x = 99% of a = 0.99 a
So, we can write:
\[{{t}_{99\text{ % } \!\!\!\!\text{ }}}=\frac{2.303}{k}\log \frac{a}{a-0.99a}\]
\[{{{t}}_{\text{99 % }\!\!\!\!\text{ }}}\text{ = }\frac{\text{2}\text{.303}}{\text{k}}\text{ log 1}{{\text{0}}^{2}}\]
\[{{t}_{\text{99%}\text{ }}}\text{ = 2}\times \frac{\text{2}\text{.303}}{\text{k}}\]
90% completion means that x = 90% of a = 0.90 a
\[{{t}_{99\text{ % } \!\!\!\!\text{ }}}=\frac{2.303}{k}\log \frac{a}{a-0.90a}\]
\[{{{t}}_{\text{99 % }\!\!\!\!\text{ }}}\text{ = }\frac{\text{2}\text{.303}}{\text{k}}\text{ log 1}{{\text{0}}^{}}\]
\[{{t}_{\text{99%}\text{ }}}\text{ =}\frac{\text{2}\text{.303}}{\text{k}}\]
Now, we can take the ratio as given below:
\[\frac{{{t}_{99\text{%}\!\!\!\!\text{ }}}}{{{t}_{90\text{%}\!\!\!\!\text{ }}}}=\frac{\left( \frac{2\text{ x 2}\text{.303}}{k} \right)}{\left( \frac{2.303}{k} \right)}\]
Hence, the time required for 99% completion of a first order reaction is twice the time required for the completion of 90% of the reaction.
19. A first order reaction takes 40 min for 30% decomposition. Calculate ${{\text{t}}_{\text{1/2}}}$.
Ans: 30% decomposition means that x = 30% of a = 0.30 a
Since, the reaction is of 1st order, we can write:
\[\text{k = }\frac{\text{2}\text{.303}}{\text{t}}\text{ log}\frac{\text{a}}{\text{a-x}}\]
Time is given as 40 min. So, putting the values, we get:
\[\text{k = }\frac{\text{2}\text{.303}}{40}\text{ log}\frac{\text{a}}{\text{a-0}\text{.30a}}\]
\[\text{k = }\frac{\text{2}\text{.303}}{40}\text{ log}\frac{10}{7}{{\min }^{-1}}\]
\[\text{k = }\frac{\text{2}\text{.303}}{40}\text{ }\!\!\times\!\!\text{ 0}\text{.1549 mi}{{\text{n}}^{-1}}=8.918\text{ }\!\!\times\!\!\text{ 1}{{\text{0}}^{-3}}{{\min }^{-1}}\]
Now, we can calculate the half-life period as we have the rate constant value.
We can write:
\[{{t}_{1/2}}=\frac{0.693}{k}=\frac{0.693}{8.918\text{ }\!\!\times\!\!\text{ 1}{{\text{0}}^{-3}}}=7.77\text{ }\min \]
So, the half-life is 7.77 min.
20. For the decomposition of azoisopropane to hexane and nitrogen at 543 K, the following data are obtained:
T (sec) | P (mm of Hg) |
0 | 35.0 |
360 | 54.0 |
720 | 63.0 |
Calculate the rate constant.
Ans: The decomposition of azoisopropane to hexane and nitrogen at 54.3 k is represented by the following equation.
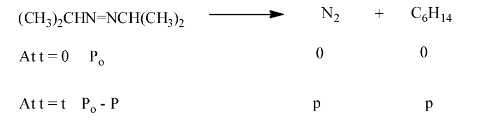
Total pressure after time t, we will be:
\[{{\text{P}}_{\text{t}}}\text{ = (}{{\text{P}}_{\text{o}}}\text{-p) + p + p}\]
\[{{\text{P}}_{\text{t}}}\text{=}{{\text{P}}_{\text{o}}}\text{+p}\]
\[\text{p=}{{\text{P}}_{\text{t}}}-{{\text{P}}_{\text{o}}}\]
Now, we can substitute the value of p for the pressure of reactant at time t
\[\text{=}{{\text{P}}_{\text{o}}}\text{-p}\]
\[\text{=}{{\text{P}}_{\text{o}}}\text{-(}{{\text{P}}_{\text{t}}}\text{-}{{\text{P}}_{\text{o}}}\text{)}\]
\[\text{= 2}{{\text{P}}_{\text{o}}}\text{ - }{{\text{P}}_{\text{t}}}\]
Now, we can apply the rate constant formula of 1st order reaction.
\[\text{k = }\frac{\text{2}\text{.303}}{\text{t}}\text{ log}\frac{\text{P}}{\text{2}{{\text{P}}_{\text{o}}}\text{-}{{\text{P}}_{\text{t}}}}\]
When t = 360 s,
Putting the values, we get:
\[\text{k = }\frac{\text{2}\text{.303}}{360}\text{ log}\frac{35.0}{\text{2 }\!\!\times\!\!\text{ 35 - 54}}=2.175\text{ }\!\!\times\!\!\text{ 1}{{\text{0}}^{-3}}\text{ }{{\text{s}}^{-1}}\]
When t = 720 s,
Putting the values, we get:
\[\text{k = }\frac{\text{2}\text{.303}}{720}\text{ log}\frac{35.0}{\text{2 }\!\!\times\!\!\text{ 35 - 63}}=2.235\text{ }\!\!\times\!\!\text{ 1}{{\text{0}}^{-3}}\text{ }{{\text{s}}^{-1}}\]
Now, we can find the average value:
\[\text{k = }\frac{\text{(2}\text{.175 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-3}}}\text{)+(2}\text{.235 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-3}}}\text{)}}{\text{2}}\text{ }{{\text{s}}^{\text{-1}}}\]
\[\text{k = 2}\text{.20 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-3}}}\text{ }{{\text{s}}^{\text{-1}}}\]
21. The following data were obtained during the first order thermal decomposition of $\text{S}{{\text{O}}_{\text{2}}}\text{C}{{\text{l}}_{\text{2}}}$ at a constant volume.
\[\text{S}{{\text{O}}_{\text{2}}}\text{C}{{\text{l}}_{{{\text{2}}_{\text{(g)}}}}}\to \text{S}{{\text{O}}_{{{\text{2}}_{\text{(g)}}}}}\text{+C}{{\text{l}}_{{{\text{2}}_{\text{(g)}}}}}\]
Experiment | Time/ s | Total pressure/ atm |
1 | 0 | 0.5 |
2 | 100 | 0.6 |
Calculate the rate of the reaction when total pressure is 0.65 atm.
Ans: The given reaction shows the thermal decomposition of $\text{S}{{\text{O}}_{\text{2}}}\text{C}{{\text{l}}_{\text{2}}}$ at constant volume.
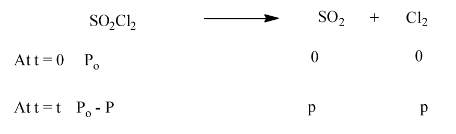
Total pressure after time t, we will be:
\[{{\text{P}}_{\text{t}}}\text{ = (}{{\text{P}}_{\text{o}}}\text{-p) + p + p}\]
\[{{\text{P}}_{\text{t}}}\text{=}{{\text{P}}_{\text{o}}}\text{+p}\]
\[\text{p=}{{\text{P}}_{\text{t}}}-{{\text{P}}_{\text{o}}}\]
Now, we can substitute the value of p for the pressure of reactant at time t
\[\text{=}{{\text{P}}_{\text{o}}}\text{-p}\]
\[\text{=}{{\text{P}}_{\text{o}}}\text{-(}{{\text{P}}_{\text{t}}}\text{-}{{\text{P}}_{\text{o}}}\text{)}\]
\[\text{= 2}{{\text{P}}_{\text{o}}}\text{ - }{{\text{P}}_{\text{t}}}\]
Now, we can apply the rate constant formula of 1st order reaction.
\[\text{k = }\frac{\text{2}\text{.303}}{\text{t}}\text{ log}\frac{\text{P}}{\text{2}{{\text{P}}_{\text{o}}}\text{-}{{\text{P}}_{\text{t}}}}\]
When the t = 100 s
\[\text{k = }\frac{\text{2}\text{.303}}{100}\text{ log}\frac{0.5}{\text{2 }\!\!\times\!\!\text{ 0}\text{.5 - 0}\text{.6}}\]
\[\text{k = 2}\text{.231 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-3}}}\text{ }{{\text{s}}^{\text{-1}}}\]
When ${{\text{P}}_{\text{t}}}$ = 0.65 atm
Therefore, pressure of $\text{S}{{\text{O}}_{\text{2}}}\text{C}{{\text{l}}_{\text{2}}}$ at time t total pressure is 0.65 atm, is
${{\text{P}}_{\text{S}{{\text{O}}_{\text{2}}}\text{C}{{\text{l}}_{\text{2}}}}}\text{=2}{{\text{P}}_{\text{o}}}\text{-}{{\text{P}}_{\text{t}}}$
= 2 $\text{ }\!\!\times\!\!\text{ }$ 0.50 – 0.65
= 0.35 atm
Therefore, the rate of equation, when total pressure is 0.65 atm, is given by:
\[\text{Rate = k(}{{\text{P}}_{\text{S}{{\text{O}}_{\text{2}}}\text{C}{{\text{l}}_{\text{2}}}}}\text{)}\]
\[\text{Rate = (2}\text{.33 x 1}{{\text{0}}^{\text{-3}}}\text{)(0}\text{.354) = 7}\text{.8 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-4}}}\text{atm }{{\text{s}}^{\text{-1}}}\]
22. The rate constant for the decomposition of ${{\text{N}}_{\text{2}}}{{\text{O}}_{\text{5}}}$ at various temperature is given below:
$\text{T}{{\text{/}}^{\text{o}}}\text{c}$ | 0 | 20 | 40 | 60 | 80 |
$\text{1}{{\text{0}}^{\text{5}}}\text{ }\!\!\times\!\!\text{ k/s}$ | 0.0787 | 1.70 | 25.7 | 178 | 2140 |
Draw a graph between ln K and 1/T and calculate the values of A and ${{\text{E}}_{\text{a}}}$. Predict the rate constant at $\text{3}{{\text{0}}^{\text{o}}}$ and $\text{5}{{\text{0}}^{\text{o}}}$C.
Ans: As the data is given we can write:
$\text{T}{{\text{/}}^{\text{o}}}\text{c}$ | 0 | 20 | 40 | 60 | 80 |
T/K | 273 | 293 | 313 | 333 | 353 |
$\frac{\text{1}}{\text{T}}\text{/}{{\text{k}}^{\text{-1}}}$ | $\text{3}\text{.66 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-3}}}$ | $\text{3}\text{.41 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-3}}}$ | $\text{3}\text{.19 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-3}}}$ | $\text{3}\text{.0 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-3}}}$ | $\text{2}\text{.83 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-3}}}$ |
$\text{1}{{\text{0}}^{\text{5}}}\text{ }\!\!\times\!\!\text{ k/s}$ | 0.0787 | 4.075 | 25.7 | 178 | 2140 |
ln K | -7.147 | -4.075 | -1.359 | -0.577 | 3.063 |
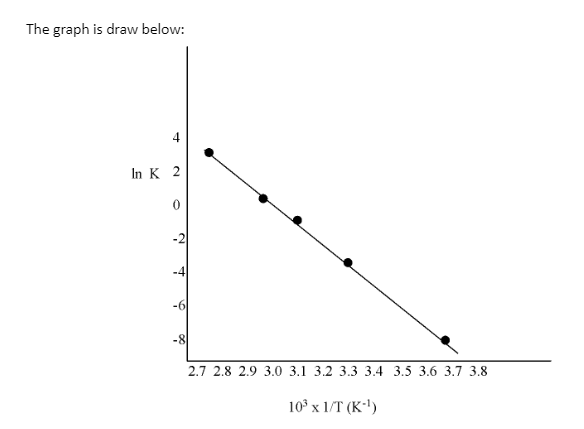
Slope of the line, will be given as:
\[\frac{{{\text{y}}_{\text{2}}}\text{-}{{\text{y}}_{\text{1}}}}{{{\text{x}}_{\text{2}}}\text{-}{{\text{x}}_{\text{1}}}}\text{ = 12}\text{.301 K}\]
According to the Arrhenius equation,
\[\text{Slope = -}\frac{{{\text{E}}_{\text{a}}}}{\text{R}}\]
\[\text{= }{{\text{E}}_{\text{a}}}\text{= -slope }\!\!\times\!\!\text{ R}\]
= (-12.301) (8.314)
\[\text{=102}\text{.27 KJ mo}{{\text{l}}^{\text{-1}}}\]
Again,
\[\text{ln k = ln A - }\frac{{{\text{E}}_{\text{a}}}}{\text{RT}}\]
\[\text{ln A = ln k + }\frac{{{\text{E}}_{\text{a}}}}{\text{RT}}\]
As T = 273 K and ln k = -7.147
Applying this in the formula, we get:
\[\text{ln A = -7}\text{.147 - }\frac{102.27\text{ }\!\!\times\!\!\text{ 1}{{\text{0}}^{3}}}{8.314\text{ }\!\!\times\!\!\text{ 273}}=37.911\]
So, \[\text{A=2}\text{.91 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{6}}}\]
When T = 30 + 273 K = 303 K
\[\frac{\text{1}}{\text{T}}\text{ = 0}\text{.0033K = 3}\text{.3 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-3}}}\text{K}\]
Now, at $\frac{\text{1}}{\text{T}}\text{ = 0}\text{.0033K = 3}\text{.3 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-3}}}\text{K}$
ln k = - 2.8
Therefore, $\text{k = 6}\text{.08 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-2}}}\text{ }{{\text{s}}^{\text{-1}}}$
When T = 50 + 273 K = 323 K
\[\frac{\text{1}}{\text{T}}\text{ = 0}\text{.0031K = 3}\text{.1 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-3}}}\text{K}\]
Now, at $\frac{\text{1}}{\text{T}}\text{ = 0}\text{.0031K = 3}\text{.1 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-3}}}\text{K}$
ln k = - 0.5
Therefore, $\text{k = 0}\text{.607 }{{\text{s}}^{\text{-1}}}$
23. The rate constant for the decomposition of hydrocarbons is $\text{2}\text{.418 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-5}}}\text{ }{{\text{s}}^{\text{-1}}}$ at 546 K. If the energy of activation is 179.9 kJ /mol, what will be the value of pre-exponential factor.
Ans: We are given some values as:
\[\text{K = 2}\text{.418 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-5}}}\text{ }{{\text{s}}^{\text{-1}}}\]
\[T = 546 K\]
\[{{\text{E}}_{\text{a}}}\text{ = 179}\text{.9 kJ mo}{{\text{l}}^{\text{-1}}}=179.9\text{ }\!\!\times\!\!\text{ 1}{{\text{0}}^{3}}\text{ J mo}{{\text{l}}^{-1}}\]
We the Arrhenius equation is:
\[\text{k = A }{{\text{e}}^{\text{-}{{\text{E}}_{\text{a}}}\text{/RT}}}\]
In the log form, this can be written as:
\[\text{ln k = ln A - }\frac{{{\text{E}}_{\text{a}}}}{\text{RT}}\]
\[\text{log k = log A - }\frac{{{\text{E}}_{\text{a}}}}{\text{2}\text{.303 RT}}\]
\[\text{log k = log (2}\text{.418 }\!\!\times\!\!\text{ 1}{{\text{0}}^{-5}}\text{) - }\frac{179.9\text{ }\!\!\times\!\!\text{ 1}{{\text{0}}^{3}}}{\text{2}\text{.303 }\!\!\times\!\!\text{ 8}\text{.314 }\!\!\times\!\!\text{ 546}}\]
= (0.3835 – 5) + 17.2082 = 12.5917
Therefore, A = antilog (12.5917)
\[\text{A = 3}\text{.912 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{12}}}\text{ }{{\text{s}}^{\text{-1}}}\]
24. Consider a certain reaction $\text{A }\to \text{ Products}$ with $\text{k = 2}\text{.0 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-2}}}\text{ }{{\text{s}}^{\text{-1}}}$. Calculate the concentration of A remaining after 100s if the initial concentration of A is $\text{1}\text{.0 mol }{{\text{L}}^{\text{-1}}}$.
Ans: We are given some values, that are given below:
\[\text{k = 2}\text{.0 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-2}}}\text{ }{{\text{s}}^{\text{-1}}}\]
\[t = 100 s\]
\[{{\text{ }\!\![\!\!\text{ A }\!\!]\!\!\text{ }}_{\text{o}}}\text{=1}\text{.0 mol }{{\text{L}}^{\text{-1}}}\]
As we can see that the units of k are given in ${{\text{s}}^{\text{-1}}}$, this means that the reaction is a first order reaction.
Therefore, we can write:
\[\text{k = }\frac{\text{2}\text{.303}}{\text{t}}\text{ log}\frac{{{\text{ }\!\![\!\!\text{ A }\!\!]\!\!\text{ }}_{\text{0}}}}{\text{ }\!\![\!\!\text{ A }\!\!]\!\!\text{ }}\]
Putting the values, we get:
\[\text{2}\text{.0 }\!\!\times\!\!\text{ 1}{{\text{0}}^{-2}}\text{ = }\frac{\text{2}\text{.303}}{100}\text{ log}\frac{1.0}{\text{ }\!\![\!\!\text{ A }\!\!]\!\!\text{ }}\]
\[\text{2}\text{.0 }\!\!\times\!\!\text{ 1}{{\text{0}}^{-2}}\text{ = }\frac{\text{2}\text{.303}}{100}\text{ (-log }\!\![\!\!\text{ A }\!\!]\!\!\text{ )}\]
\[\text{(-log }\!\![\!\!\text{ A }\!\!]\!\!\text{ ) = }\frac{\text{2}\text{.0 }\!\!\times\!\!\text{ 1}{{\text{0}}^{-2}}\text{ }\!\!\times\!\!\text{ 100}}{2.303}\]
\[\text{ }\!\![\!\!\text{ A }\!\!]\!\!\text{ =antilog }\left( \frac{\text{2}\text{.0 }\!\!\times\!\!\text{ 1}{{\text{0}}^{-2}}\text{ }\!\!\times\!\!\text{ 100}}{2.303} \right)\]
\[=0.135\text{ mol }{{\text{L}}^{-1}}\]
Therefore, the remaining amount of A is $0.135\text{ mol }{{\text{L}}^{-1}}$.
25. Sucrose decomposes in acid solution into glucose and fructose according to the first order rate law with${{\text{t}}_{\text{1/2}}}\text{ = 3}\text{.00 hours}$. What fraction of a sample of sucrose remains after 8 hours?
Ans: The given reaction is a first order reaction. So, we can write:
\[\text{k = }\frac{\text{2}\text{.303}}{\text{t}}\text{ log}\frac{{{\text{ }\!\![\!\!\text{ R }\!\!]\!\!\text{ }}_{\text{0}}}}{\text{ }\!\![\!\!\text{ R }\!\!]\!\!\text{ }}\]
It is given that the half-life is 3 hours. Therefore, we can write:
\[\text{k = }\frac{\text{0}\text{.693}}{{{\text{t}}_{\text{1/2}}}}\]
So, putting the values in this, we get:
\[\text{k = }\frac{\text{0}\text{.693}}{\text{3}}\text{ = 0}\text{.231 }{{\text{h}}^{\text{-1}}}\]
Now, we can put this value of rate constant in the first order reaction formula.
\[\text{0}\text{.231 = }\frac{\text{2}\text{.303}}{8}\text{ log}\frac{{{\text{ }\!\![\!\!\text{ R }\!\!]\!\!\text{ }}_{\text{0}}}}{\text{ }\!\![\!\!\text{ R }\!\!]\!\!\text{ }}\]
\[\text{log}\frac{{{\text{ }\!\![\!\!\text{ R }\!\!]\!\!\text{ }}_{\text{0}}}}{\text{ }\!\![\!\!\text{ R }\!\!]\!\!\text{ }}\text{ = }\frac{\text{0}\text{.231 }\!\!\times\!\!\text{ 8}}{2.303}\text{ }\]
\[\text{log}\frac{{{\text{ }\!\![\!\!\text{ R }\!\!]\!\!\text{ }}_{\text{0}}}}{\text{ }\!\![\!\!\text{ R }\!\!]\!\!\text{ }}\text{ = 0}\text{.8024}\]
\[\frac{{{\text{ }\!\![\!\!\text{ R }\!\!]\!\!\text{ }}_{\text{0}}}}{\text{ }\!\![\!\!\text{ R }\!\!]\!\!\text{ }}\text{ = antilog (0}\text{.8024)}\]
\[\frac{{{\text{ }\!\![\!\!\text{ R }\!\!]\!\!\text{ }}_{\text{0}}}}{\text{ }\!\![\!\!\text{ R }\!\!]\!\!\text{ }}\text{ = 6}\text{.3445}\]
Or we can write:
\[\frac{\text{ }\!\![\!\!\text{ R }\!\!]\!\!\text{ }}{{{\text{ }\!\![\!\!\text{ R }\!\!]\!\!\text{ }}_{0}}}\text{ = 0}\text{.158}\]
Therefore, the fraction of sample of sucrose that remains after 8 hours is 0.158.
26. The decomposition of hydrocarbon follows the equation $\text{k = (4}\text{.5 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{11}}}\text{ }{{\text{s}}^{\text{-1}}}\text{)}{{\text{e}}^{\text{-280000K/T}}}$. Calculate ${{\text{E}}_{\text{a}}}$.
Ans: According to the Arrhenius equation,
\[\text{k = A}{{\text{e}}^{\text{-}{{\text{E}}_{\text{a}}}\text{/RT}}}\]
We are given the equation as:
\[\text{k = (4}\text{.5 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{11}}}\text{ }{{\text{s}}^{\text{-1}}}\text{)}{{\text{e}}^{\text{-280000K/T}}}\]
Therefore, the formula can be written as:
\[\text{-}\frac{{{\text{E}}_{\text{a}}}}{\text{RT}}\text{ = -}\frac{\text{28000 K}}{\text{T}}\]
This can be written as:--------
\[{{\text{E}}_{\text{a}}}\text{ = 28000 }\!\!\times\!\!\text{ R}\]
\[{{\text{E}}_{\text{a}}}\text{ = 28000 }\!\!\times\!\!\text{ 8}\text{.314 = 232}\text{.79 kJ mo}{{\text{l}}^{\text{-1}}}\]
Therefore, the value of ${{\text{E}}_{\text{a}}}$ is $\text{232}\text{.79 kJ mo}{{\text{l}}^{\text{-1}}}$
27. The rate constant for the first order decomposition of ${{\text{H}}_{\text{2}}}{{\text{O}}_{\text{2}}}$ is given by the following equation:
$\text{log k = 14}\text{.34 - 1}\text{.25 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{4}}}\text{ K/T}$
Calculate ${{\text{E}}_{\text{a}}}$ for this reaction and at what temperature will its half-period be 256 minutes?
Ans: According to the Arrhenius equation,
\[\text{k = A}{{\text{e}}^{\text{-}{{\text{E}}_{\text{a}}}\text{/RT}}}\]
This can be written as:
\[\text{ln k = ln A - }\frac{{{\text{E}}_{\text{a}}}}{\text{RT}}\]
In the log form it can be written as:
\[\text{log k = log A - }\frac{{{\text{E}}_{\text{a}}}}{\text{2}\text{.303 RT}}\]
We are given:
\[\text{log k = 14}\text{.34 - 1}\text{.25 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{4}}}\text{ K/T}\]
Comparing these two, we get:
\[\frac{{{\text{E}}_{\text{a}}}}{\text{2}\text{.303 RT}}\text{ = }\frac{\text{1}\text{.25 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{4}}}\text{ K}}{\text{T}}\]
\[{{\text{E}}_{\text{a}}}\text{ = 2}\text{.303 R }\!\!\times\!\!\text{ 1}\text{.25 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{4}}}\text{ K}\]
\[{{\text{E}}_{\text{a}}}\text{ = 2}\text{.303 }\!\!\times\!\!\text{ 8}\text{.314 }\!\!\times\!\!\text{ 1}\text{.25 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{4}}}\text{ K}\]
\[{{\text{E}}_{\text{a}}}\text{ = 239}\text{.34 kJ mo}{{\text{l}}^{-1}}\]
We are given a half-life of 256 minutes.
\[\text{k = }\frac{\text{0}\text{.693}}{{{\text{t}}_{\text{1/2}}}}\]
\[\text{k = }\frac{\text{0}\text{.693}}{\text{256 }\!\!\times\!\!\text{ 60}}\text{ = 4}\text{.51 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-5}}}\text{ }{{\text{s}}^{\text{-1}}}\]
Now, we have the value of rate constant, we can put in the equation:
\[\text{log(4}\text{.51 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-5}}}\text{) = 14}\text{.34 - }\frac{\text{1}\text{.25 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{4}}}}{\text{T}}\]
T = 669 K
28. The decomposition of A into product has value of k as $\text{4}\text{.5 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{3}}}\text{ }{{\text{s}}^{\text{-1}}}$ at $\text{1}{{\text{0}}^{\text{o}}}\text{C}$ and energy of activation $\text{60 kJ mo}{{\text{l}}^{\text{-1}}}$. At what temperature would k be $\text{1}\text{.5 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{4}}}\text{ }{{\text{s}}^{\text{-1}}}$?
Ans: We are some information:
\[{{\text{k}}_{\text{1}}}\text{ = 4}\text{.5 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{3}}}\]
\[{{\text{T}}_{\text{1}}}\text{ = 10 + 273 = 283 K}\]
\[{{\text{k}}_{2}}\text{ = 1}\text{.5 }\!\!\times\!\!\text{ 1}{{\text{0}}^{4}}\]
\[{{\text{T}}_{\text{2}}}=?\]
\[{{\text{E}}_{\text{a}}}\text{ = 60 kJ mo}{{\text{l}}^{\text{-1}}}\]
Applying Arrhenius equation:
\[\text{log}\frac{{{\text{k}}_{\text{2}}}}{{{\text{k}}_{\text{1}}}}\text{ = }\frac{{{\text{E}}_{\text{a}}}}{\text{2}\text{.303R}}\left( \frac{{{\text{T}}_{\text{2}}}\text{-}{{\text{T}}_{\text{1}}}}{{{\text{T}}_{\text{1}}}{{\text{T}}_{\text{2}}}} \right)\]
Putting the values, we can write:
\[\text{log}\frac{1.5\text{ }\!\!\times\!\!\text{ 1}{{\text{0}}^{4}}}{4.5\text{ }\!\!\times\!\!\text{ 1}{{\text{0}}^{3}}}\text{ = }\frac{60}{\text{2}\text{.303 }\!\!\times\!\!\text{ 8}\text{.314}}\left( \frac{{{\text{T}}_{\text{2}}}\text{-283}}{\text{283}{{\text{T}}_{\text{2}}}} \right)\]
\[\text{log 3}\text{.333 = 3133}\text{.63}\left( \frac{{{\text{T}}_{\text{2}}}\text{-283}}{\text{283}{{\text{T}}_{\text{2}}}} \right)\]
\[\frac{0.5228}{3133.63}=\left( \frac{{{\text{T}}_{\text{2}}}\text{-283}}{\text{283}{{\text{T}}_{\text{2}}}} \right)\]
\[\text{0}\text{.0472}{{\text{T}}_{\text{2}}}\text{ = }{{\text{T}}_{\text{2}}}\text{ - 283}\]
\[{{\text{T}}_{\text{2}}}\text{ = 297 K }\]
Or we can write:
\[{{\text{T}}_{\text{2}}}\text{ = 2}{{\text{4}}^{\text{o}}}\text{C}\]
29. The time required for 10% completion of a first order reaction at 298 k is equal to that required for its 25% completion at 308 K. If the value of A is $\text{4 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{10}}}\text{ }{{\text{s}}^{\text{-1}}}$ , Calculate k at 318 K and ${{\text{E}}_{\text{a}}}$.
Ans: There are two cases in this question. As the reaction given is first order reaction, we can use:
\[\text{k = }\frac{\text{2}\text{.303}}{\text{t}}\text{ log}\frac{\text{a}}{\text{a-x}}\]
For case 1:
\[{{\text{k}}_{\text{298K}}}\text{ = }\frac{\text{2}\text{.303}}{{{\text{t}}_{\text{1}}}}\text{ log}\frac{\text{a}}{\text{a - 0}\text{.10a}}\]
\[{{\text{k}}_{\text{298K}}}\text{ = }\frac{\text{2}\text{.303}}{{{\text{t}}_{\text{1}}}}\text{ log}\frac{10}{9}\]
\[{{\text{k}}_{\text{298K}}}\text{ = }\frac{\text{2}\text{.303}}{{{\text{t}}_{\text{1}}}}\text{ }\!\!\times\!\!\text{ 0}\text{.0458}\]
\[{{\text{t}}_{\text{1}}}\text{ = }\frac{\text{0}\text{.1055}}{{{\text{k}}_{\text{298K}}}}\]
For case 2:
\[{{\text{k}}_{\text{308K}}}\text{ = }\frac{\text{2}\text{.303}}{{{\text{t}}_{2}}}\text{ log}\frac{\text{a}}{\text{a - 0}\text{.25a}}\]
\[{{\text{k}}_{\text{308K}}}\text{ = }\frac{\text{2}\text{.303}}{{{\text{t}}_{2}}}\text{ log}\frac{4}{3}\]
\[{{\text{k}}_{\text{308K}}}\text{ = }\frac{\text{2}\text{.303}}{{{\text{t}}_{2}}}\text{ }\!\!\times\!\!\text{ 0}\text{.125}\]
\[{{\text{t}}_{2}}\text{ = }\frac{\text{0}\text{.2879}}{{{\text{k}}_{\text{308K}}}}\]
But ${{\text{t}}_{\text{1}}}\text{ = }{{\text{t}}_{\text{2}}}$
Hence,
\[\frac{\text{0}\text{.1055}}{{{\text{k}}_{\text{298K}}}}\text{ = }\frac{\text{0}\text{.2879}}{{{\text{k}}_{\text{308K}}}}\]
\[\frac{{{\text{k}}_{\text{308K}}}}{{{\text{k}}_{\text{298K}}}}\text{ = 2}\text{.7289}\]
Now, applying the Arrhenius equation,
\[\text{log}\frac{{{\text{k}}_{\text{308K}}}}{{{\text{k}}_{\text{298K}}}}\text{ = }\frac{{{\text{E}}_{\text{a}}}}{\text{2}\text{.303R}}\left( \frac{{{\text{T}}_{\text{2}}}\text{-}{{\text{T}}_{\text{1}}}}{{{\text{T}}_{\text{1}}}{{\text{T}}_{\text{2}}}} \right)\]
\[\text{log(2}\text{.7289) = }\frac{{{\text{E}}_{\text{a}}}}{\text{2}\text{.303 }\!\!\times\!\!\text{ 8}\text{.314}}\left( \frac{\text{308-298}}{298\text{ }\!\!\times\!\!\text{ 308}} \right)\]
\[{{\text{E}}_{\text{a}}}\text{ = 76}\text{.623 kJ mo}{{\text{l}}^{\text{-1}}}\]
Now, the calculation of k at 318 K
\[\text{log k = log A - }\frac{{{\text{E}}_{\text{a}}}}{\text{2}\text{.303RT}}\]
\[\text{log k = log (4 }\!\!\times\!\!\text{ 1}{{\text{0}}^{10}}\text{) - }\frac{7623}{\text{2}\text{.303 }\!\!\times\!\!\text{ 8}\text{.314 }\!\!\times\!\!\text{ 318}}\]
\[\text{log k = 10}\text{.6021 - 12}\text{.5843 = -1}\text{.9822}\]
k = Antilog (-1.9822) = $\text{antilog (\bar{2}}\text{.0178) = 1}\text{.042 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-2}}}\text{ }{{\text{s}}^{\text{-1}}}$
Therefore, k is $\text{1}\text{.042 }\!\!\times\!\!\text{ 1}{{\text{0}}^{\text{-2}}}\text{ }{{\text{s}}^{\text{-1}}}$.
30. The rate of a reaction quadruples when the temperature changes from 293 K to 313 K. Calculate the energy of activation of the reaction assuming that it does not change with temperature.
Ans: We are given that:
\[{{\text{k}}_{\text{2}}}\text{ = 4 }{{\text{k}}_{\text{1}}}\]
\[{{\text{T}}_{\text{1}}}\text{ = 293K}\]
\[{{\text{T}}_{2}}\text{ = 313K}\]
According the Arrhenius equation, we get:
\[\text{log}\frac{{{\text{k}}_{2}}}{{{\text{k}}_{1}}}\text{ = }\frac{{{\text{E}}_{\text{a}}}}{\text{2}\text{.303R}}\left( \frac{{{\text{T}}_{\text{2}}}\text{-}{{\text{T}}_{\text{1}}}}{{{\text{T}}_{\text{1}}}{{\text{T}}_{\text{2}}}} \right)\]
Putting the values, we get:
\[\text{log}\frac{\text{4}{{\text{k}}_{1}}}{{{\text{k}}_{1}}}\text{ = }\frac{{{\text{E}}_{\text{a}}}}{\text{2}\text{.303 }\!\!\times\!\!\text{ 8}\text{.314}}\left( \frac{\text{313-293}}{293\text{ }\!\!\times\!\!\text{ 313}} \right)\]
\[\text{0}\text{.6021 = }\frac{{{\text{E}}_{\text{a}}}}{\text{2}\text{.303 }\!\!\times\!\!\text{ 8}\text{.314}}\left( \frac{\text{313-293}}{293\text{ }\!\!\times\!\!\text{ 313}} \right)\]
\[{{\text{E}}_{\text{a}}}\text{=}\frac{\text{0}\text{.6021 }\!\!\times\!\!\text{ 2}\text{.303 }\!\!\times\!\!\text{ 8}\text{.314 }\!\!\times\!\!\text{ 293 }\!\!\times\!\!\text{ 313}}{\text{20}}\]
\[{{\text{E}}_{\text{a}}}\text{ = 52863}\text{.00 J mo}{{\text{l}}^{\text{-1}}}\]
\[{{\text{E}}_{\text{a}}}\text{ = 52}\text{.863 kJ mo}{{\text{l}}^{\text{-1}}}\]
Therefore, the required activation energy is $\text{52}\text{.863 kJ mo}{{\text{l}}^{\text{-1}}}$.
Class 12 Chemistry Chapter 3 NCERT Solutions Quick Overview of Topics
Class 12 Chemistry Chapter 3 NCERT Solutions - Quick Overview of Detailed Structure of Topics and Subtopics Covered.
Topic | Subtopics |
Introduction to Chemical Kinetics | Definition and importance |
Rate of a Chemical Reaction | Average and instantaneous rate |
Factors Influencing Rate of Reaction | Concentration, temperature, pressure, catalysts |
Integrated Rate Equations | First-order, second-order, and zero-order reactions,Pseudo First Order Reaction |
Half-life of a Reaction | Definition and determination |
Collision Theory | Concept and factors affecting reaction rate |
Activation Energy and Arrhenius Equation | Activation energy, Arrhenius equation |
Temperature Dependence of Reaction Rate | Effect of temperature on rate |
Catalysis | Homogeneous and heterogeneous catalysis |
Enzyme Catalysis | Introduction to enzymatic reactions |
Class 12 Chemistry Chapter 3 NCERT Solutions Important Formulas
Class 12 NCERT solutions help the students to go through the formulas easily. Here find the Important formulas of Chapter 3- Chemical Kinetics to crack your exams.
Integrated rate law equation for zero order reaction
\[ k = \frac{[R]_o[R]}{t} \]
Where k is the rate constant and [R] is the initial molar concentration.
\[ t_{1/2} = \frac{[R]_o}{2k} \]
t1/2 is the half-life period of zero-order reaction.
Integrated rate law equation for first order reaction
k = 2.303/k log [R]/[R]
Where k is the rate constant, [R] is the initial molar concentration, and [R] is the final concentration at a time 't'.
Half-life period (t1/2) for the first-order reaction:
t1/2 = 0.693/k
Arrhenius equation
k=Ae-Ea/RT
Where 'A' is the frequency factor, Ea is the energy of activation, R is the universal gas constant and T is the absolute temperature.
Benefits of Referring to Vedantu’s NCERT Solutions for Class 12 Chemistry
The Vedantu’s Class 12 NCERT Solutions of Chemistry provided here in PDFs offer various benefits, including:
The answers provided here are straightforward.
It provides the Concise Notes and saves a lot of time for Revision.
To facilitate comprehension, solutions are presented in phases.
All of the questions from each chapter are answered.
For effective preparations, comprehend all of the processes outlined in the answers.
Important Links for Class 12 Chemistry Chapter 3 Chemical Kinetics
Students can access extra study materials on Chemical Kinetics , These resources are available for download, offering additional support for your studies.
S.No | Related Links for Class 12 Chemistry Chapter 3: Chemical Kinetics |
1. | |
2. | |
3. |
Conclusion:
Vedantu's Class 12 Chemistry Chemical Kinetics NCERT Solutions offer a comprehensive and valuable resource for students studying this subject. The solutions provided are well-structured, easy to understand, and cover all the important topics and concepts outlined in the NCERT textbook. The explanations are concise yet thorough, ensuring that students grasp the underlying principles of chemical kinetics effectively. Additionally, Vedantu's solutions provide ample practice exercises and examples to reinforce learning and help students develop problem-solving skills. Overall, Vedantu's Class 12 Chemistry Chemical Kinetics NCERT Solutions serve as a reliable companion for students, enabling them to enhance their understanding and performance in this critical area of study.
NCERT Solutions Class 12 Chemistry | Chapter-wise Links
Access Vedantu’s chapter-wise NCERT Chemistry Class 12 Solutions PDFs below for all other chapters.
S.No. | NCERT Solutions Class 12 Chemistry Chapter-wise List |
1 | |
2 | |
3 | |
4 | |
5 | |
6 | |
7 | Chapter 8 - Aldehydes, Ketones and Carboxylic Acids Solutions |
8 | |
9 |
NCERT Solutions Class 12 Chemistry - Related Links
S.No | Important Resources Links for Class 12 Chemistry |
1 | |
2 | |
3 | |
4 | |
5 |
FAQs on NCERT Solutions For Class 12 Chemistry Chapter 3 Chemical Kinetics - 2025-26
1. How can the order of a reaction be differentiated from its molecularity?
Distinguish them by remembering that order is an experimental value found from the rate law, which can be zero, fractional, or an integer. Molecularity is a theoretical concept, representing the number of reacting species in an elementary step, and must be a positive integer (1, 2, or 3).
2. How is the order of a reaction determined from experimental data?
To determine the reaction order from a table of experimental data, use the initial rates method. This involves comparing how the initial reaction rate changes when the concentration of one reactant is altered while others are kept constant.
3. How can the NCERT Solutions for Class 12 Chemical Kinetics be downloaded as a PDF?
Download the free PDF of the NCERT Solutions by visiting the Vedantu page for Class 12 Chemistry Chemical Kinetics. Click the “Download PDF” button, register with your contact details if prompted, and the file will be saved to your device for offline access and easy revision.
4. What is the process for calculating activation energy (Ea) using the Arrhenius equation?
Calculate the activation energy (Ea) by using the Arrhenius equation with rate constants measured at two different temperatures. This method allows you to quantify the minimum energy required for a reaction to occur.
Formula: The key equation to use is log(k₂/k₁) = Ea / (2.303R) * [(T₂ - T₁) / (T₁T₂)].
- Identify the two rate constants (k₁ and k₂) and their corresponding temperatures (T₁ and T₂).
- Ensure temperatures are converted to Kelvin (K = °C + 273.15).
- Substitute the values of k₁, k₂, T₁, and T₂ into the Arrhenius equation.
- Use the value of the gas constant R as 8.314 J K⁻¹ mol⁻¹.
- Solve the equation algebraically for Ea.
5. How are the units of a rate constant for a reaction determined?
Find the units of a rate constant (k) using the general formula: Units = (concentration)¹⁻ⁿ (time)⁻¹, where 'n' is the overall reaction order. For concentration in mol L⁻¹ and time in s, the units for a zero-order reaction (n=0) are mol L⁻¹ s⁻¹ and for a first-order reaction (n=1) are s⁻¹.
6. How can NCERT Solutions be used effectively to solve numerical problems?
Use the NCERT Solutions for Class 12 Chemistry Chapter 3 to master numericals by following a structured practice method. First, attempt to solve the problem on your own without looking at the solution. This helps identify your weak points.
Read the question carefully and list all the given data and what you need to find.
Identify the correct formula from the chapter (e.g., integrated rate law, Arrhenius equation).
Solve the problem step-by-step, showing all your calculations clearly.
Once finished, compare your method and final answer with the detailed solution provided.
7. What is the best way to check answers for in-text questions in Chapter 3?
First, answer the in-text question yourself using your textbook and notes. Then, refer to a reliable Class 12 Chemistry Chapter 3 question answer guide to cross-verify your logic, steps, and final result. This confirms your understanding before you move to the next topic.
8. How do you plot and interpret graphs for zero and first-order reactions?
To plot graphs for reaction kinetics, you must use the correct integrated rate equation for the given order. These graphs visually represent the relationship between reactant concentration and time, helping to identify the reaction order.
Steps for a Zero-Order Reaction:
Use the equation: [R] = -kt + [R]₀.
Plot reactant concentration [R] on the y-axis against time (t) on the x-axis.
The result will be a straight line with a negative slope.
Interpretation: The slope of the line is equal to -k, and the y-intercept is the initial concentration, [R]₀.
Steps for a First-Order Reaction:
Use the equation: ln[R] = -kt + ln[R]₀.
Plot the natural logarithm of concentration (ln[R]) on the y-axis against time (t) on the x-axis.
This also yields a straight line with a negative slope.
Interpretation: The slope is equal to -k, and the y-intercept is ln[R]₀.
9. How is the half-life of a first-order reaction calculated?
Calculate the half-life (t₁/₂) for a first-order reaction using the formula t₁/₂ = 0.693 / k, where 'k' is the rate constant. This calculation is unique because the half-life is independent of the initial concentration of the reactant. Ensure 'k' has the correct units (s⁻¹ or min⁻¹).
10. How can the solved exercises be used for effective revision?
To revise effectively, use the complete set of chemical kinetics class 12 questions and answers for focused practice. This method helps reinforce concepts and prepare for exam-style questions.
Start by downloading the Free PDF of the solutions to use offline. This allows you to study without distractions and access the material anywhere, anytime.


























