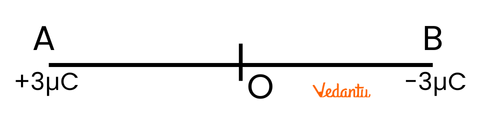Electric Charges and Fields Class 12 Extra Questions and Answers Free PDF Download



FAQs on CBSE Important Questions for Class 12 Physics Electric Charges and Fields - 2025-26
1. What are the most important topics in Chapter 1, Electric Charges and Fields, for the Class 12 board exams 2025-26?
For the CBSE Class 12 board exams, the most important topics from this chapter include:
- Coulomb's Law: Both the scalar and vector forms, and its application in superposition principle problems.
- Electric Field: Properties of electric field lines, and derivations for the field due to an electric dipole on its axial and equatorial lines.
- Gauss's Law: The statement of the law and its applications to find the electric field for an infinitely long straight wire, a uniformly charged infinite plane sheet, and a thin spherical shell.
- Electric Dipole: The concept of a dipole in a uniform external field and the derivation for the torque it experiences.
2. State the basic properties of electric charge that are crucial for solving numerical problems.
The three most fundamental properties of electric charge are:
- Additive Nature of Charge: The total charge of a system is the algebraic sum of all individual charges present in the system.
- Conservation of Charge: The total charge of an isolated system remains constant. Charge can neither be created nor destroyed; it can only be transferred from one body to another.
- Quantisation of Charge: All free charges are integral multiples of a basic unit of charge, denoted by 'e'. The charge 'q' on a body is always given by q = ne, where n is any integer (positive or negative) and e = 1.6 × 10⁻¹⁹ C.
3. What is the importance of expressing Coulomb's Law in its vector form?
Expressing Coulomb's Law in vector form is important because it provides two key pieces of information that the scalar form does not:
- Direction of Force: It specifies the exact direction of the electrostatic force. For example, it shows that for like charges the force is repulsive (directed away), and for unlike charges, it is attractive (directed towards).
- Compliance with Newton's Third Law: The vector form explicitly shows that the force exerted by charge q1 on q2 is equal in magnitude and opposite in direction to the force exerted by q2 on q1 (F₁₂ = -F₂₁), thus proving it obeys Newton's Third Law of Motion. This is essential for problems involving the superposition principle with multiple charges.
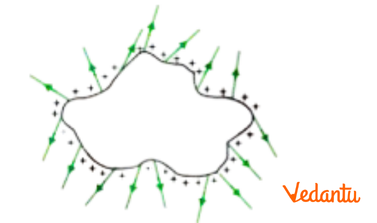
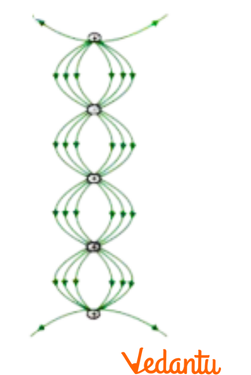
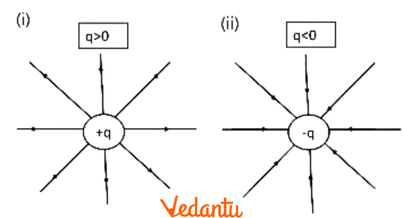
4. Why can two electric field lines never intersect each other?
Two electric field lines can never cross or intersect each other. If they did, it would mean that at the point of intersection, there are two different directions for the electric field, which is physically impossible. A tangent drawn at any point on an electric field line gives the direction of the net electric field at that point. At an intersection point, two tangents could be drawn, implying two resultant field directions, which contradicts the unique nature of the electric field at any given point.
5. If electric field lines are purely imaginary constructs, why are they considered such a crucial tool in electrostatics?
While electric field lines are indeed imaginary, they are a powerful visualisation tool for several reasons:
- Directional Information: They provide an intuitive way to represent the direction of the electric field at any point in space.
- Strength Representation: The density of the field lines (how close they are to each other) in a region gives a qualitative measure of the strength of the electric field. Denser lines indicate a stronger field, while sparse lines indicate a weaker field.
- Force Visualisation: They help in visualising the path a positive test charge would take if placed in the field, making it easier to understand the nature of forces in a complex charge system.
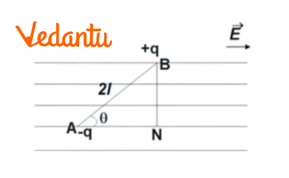
6. Derive the expression for the torque experienced by an electric dipole placed in a uniform electric field. In which orientation is the torque maximum?
When an electric dipole with dipole moment p is placed in a uniform electric field E at an angle θ, the forces on the two charges (+q and -q) are equal and opposite (qE), forming a couple. The torque (τ) acting on the dipole is the product of one force and the perpendicular distance between them.
τ = Force × Perpendicular distance
τ = (qE) × (2a sinθ)
Since dipole moment p = q × 2a, the expression becomes:
τ = pE sinθ
In vector form, τ = p × E.
The torque is maximum when sinθ is maximum, which is 1. This occurs when θ = 90°, i.e., when the dipole is placed perpendicular to the direction of the electric field.
7. How does the behaviour of an electric dipole differ when placed in a uniform electric field versus a non-uniform electric field?
The behaviour differs significantly:
- In a Uniform Electric Field: The net force on the dipole is zero because the forces on the positive and negative charges are equal and opposite, cancelling each other out. However, these forces form a couple, resulting in a net torque (unless θ = 0° or 180°), which tends to align the dipole with the field.
- In a Non-Uniform Electric Field: The forces on the charges are unequal in magnitude. Therefore, the dipole experiences both a net torque and a net force. This causes the dipole to have both rotational and translational motion.
8. State Gauss's law in electrostatics and apply it to derive the electric field due to a uniformly charged, infinite plane sheet.
Gauss's Law states that the total electric flux (Φ) through any closed surface (Gaussian surface) is equal to 1/ε₀ times the net charge (q_enclosed) enclosed by the surface.
Mathematically, Φ = ∮ E ⋅ dA = q_enclosed / ε₀.
To find the electric field (E) due to an infinite plane sheet with uniform surface charge density σ, we consider a cylindrical Gaussian surface that pierces the sheet. The electric field lines are perpendicular to the sheet.
The flux passes only through the two circular caps of the cylinder (Area A each).
Φ = E⋅A + E⋅A = 2EA
The charge enclosed by the cylinder is q = σA.
Applying Gauss's Law: 2EA = σA / ε₀.
This gives E = σ / 2ε₀. The field is uniform and does not depend on the distance from the sheet.
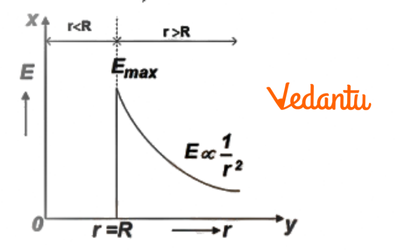
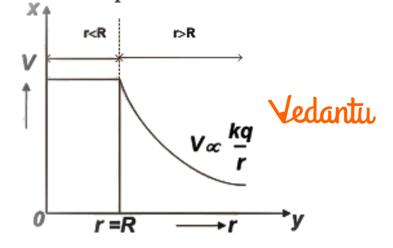
9. A hollow, conducting spherical shell is given a charge Q. What is the electric field at a point (i) inside the shell, (ii) on its surface, and (iii) outside it?
For a uniformly charged hollow spherical shell of radius R and charge Q:
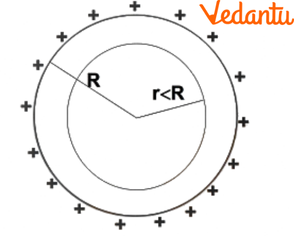
- (i) Inside the shell (r < R): The electric field is zero. According to Gauss's law, a Gaussian surface drawn inside the shell encloses no charge (q_enclosed = 0), so E = 0.
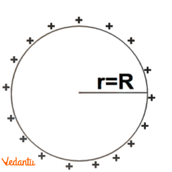
- (ii) On the surface of the shell (r = R): The electric field is maximum and is given by E = kQ / R², where k = 1/(4πε₀).
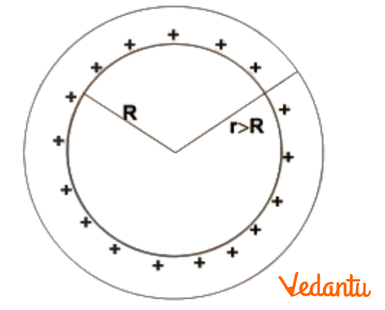
- (iii) Outside the shell (r > R): The electric field is given by E = kQ / r². The shell behaves as if the entire charge Q is concentrated at its centre.
10. Why is the net electric flux through a closed Gaussian surface zero if no charge is enclosed, even when the surface is placed in a strong external electric field?
According to Gauss's law, the net flux is directly proportional to the enclosed charge. If there is no charge inside the closed surface, the net flux must be zero. In a uniform external electric field, every electric field line that enters the closed surface must also leave it. The flux entering the surface is considered negative, and the flux leaving is considered positive. Since the number of lines entering equals the number of lines leaving, the net flux (the algebraic sum of entering and leaving flux) is zero.
11. What kind of High-Order Thinking Skills (HOTS) questions can be expected from 'Electric Charges and Fields' in the board exam?
HOTS questions from this chapter often test the deep conceptual understanding and application of principles. Examples include:
- Questions on the motion of a charged particle in a uniform electric field, linking it to projectile motion (e.g., calculating deflection).
- Problems involving a non-uniform electric field and its effect on a dipole (both force and torque).
- Conceptual questions about electrostatic shielding and its practical applications.
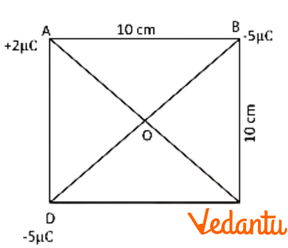
- Problems where Coulomb's law and the superposition principle are applied in complex geometrical arrangements (e.g., finding the force on a charge at the centroid of a triangle or centre of a square).
- Questions based on Earnshaw's theorem, asking why a charge cannot be in stable equilibrium under electrostatic forces alone.
12. Which derivations from Chapter 1 are most important for the CBSE Class 12 Physics exam?
For the board exam, students must focus on the following key derivations from this chapter:
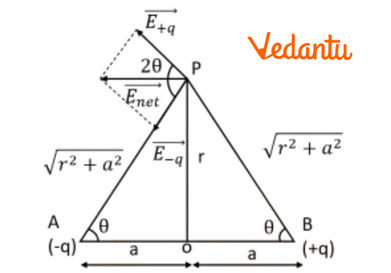
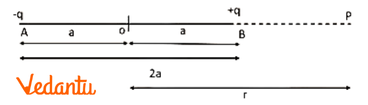
- Derivation of the electric field of a dipole at a point on its axial line and equatorial line.
- Derivation of the torque on an electric dipole in a uniform electric field.
- Application of Gauss's Law to derive the electric field for an infinitely long straight wire, a uniformly charged infinite plane sheet, and a uniformly charged thin spherical shell (for points inside, on the surface, and outside).
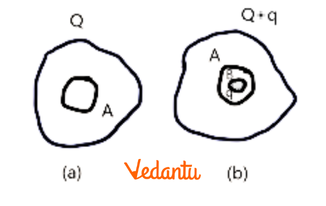
13. Explain the principle of electrostatic shielding and give a practical application.
The principle of electrostatic shielding states that the electric field inside a cavity of any conductor is always zero, regardless of the charge on the conductor or any external electric fields. When a conductor is placed in an external electric field, the free charges within it rearrange themselves on the surface in such a way that they cancel out the external field inside the conductor.
Practical Application: This principle is used to protect sensitive electronic instruments from external electrical interference. The instrument is enclosed in a metal box or cage (a Faraday cage). During a thunderstorm, it is safer to be inside a car or a bus than in the open, as the metal body of the vehicle acts as a shield against lightning.
14. A student claims that a point charge can be held in stable equilibrium by only the electrostatic forces of other fixed point charges. Why is this claim incorrect?
This claim is incorrect due to a principle known as Earnshaw's Theorem. The theorem states that a collection of point charges cannot be maintained in a stable stationary equilibrium configuration solely by the electrostatic interaction of the charges. For an equilibrium to be stable, if the charge is slightly displaced, a restoring force must pull it back to its original position from all possible directions. However, due to the nature of electrostatic fields (governed by Gauss's law), it's impossible for the electric field to be directed inwards towards a single point from all directions in free space. Therefore, the equilibrium at a null point is always unstable.