Science Class 10 Chapter 12 Questions and Answers - Free PDF Download
NCERT Solutions For Class 10 Science Chapter 12 Electricity - 2025-26



FAQs on NCERT Solutions For Class 10 Science Chapter 12 Electricity - 2025-26
1. Where can I find reliable and step-by-step NCERT Solutions for Class 10 Science Chapter 11, Electricity, for the 2025-26 session?
You can find comprehensive and accurate NCERT Solutions for Class 10 Science Chapter 11 (Electricity) on Vedantu's website. These solutions are prepared by subject matter experts and provide detailed, step-by-step explanations for all in-text and exercise questions, fully aligned with the latest CBSE 2025-26 syllabus. They are designed to help you understand the correct methodology for solving problems.
2. What is the step-by-step method to calculate the number of electrons that constitute one coulomb of charge, as per the NCERT textbook?
To solve this, you need to use the charge of a single electron. The correct method is as follows:
- Step 1: Identify the charge of one electron (e), which is 1.6 × 10⁻¹⁹ C.
- Step 2: Use the formula for total charge, Q = n × e, where 'Q' is the total charge (1 C) and 'n' is the number of electrons.
- Step 3: Rearrange the formula to solve for 'n': n = Q / e.
- Step 4: Substitute the values: n = 1 / (1.6 × 10⁻¹⁹).
- Step 5: Calculate the result: n = 6.25 × 10¹⁸ electrons.
Therefore, 6.25 × 10¹⁸ electrons constitute one coulomb of charge.
3. On which four factors does the resistance of a conductor depend, according to the NCERT solutions for Chapter 11?
The resistance of a conductor is a fundamental property that depends on four key factors:
- Length of the conductor (l): Resistance is directly proportional to the length. A longer wire has more resistance.
- Area of cross-section (A): Resistance is inversely proportional to the cross-sectional area. A thicker wire has less resistance.
- Nature of the material (ρ): This is represented by resistivity, a characteristic property of the material. Materials like copper have low resistivity, while alloys like nichrome have high resistivity.
- Temperature: For most conductors, resistance increases with an increase in temperature.
4. Why are the heating elements of devices like electric toasters made of an alloy instead of a pure metal?
The use of alloys for heating elements is a deliberate design choice based on two main properties explained in the NCERT solutions:
- High Resistivity (ρ): Alloys, such as nichrome, have a much higher resistivity than pure metals like copper. According to Joule's law of heating (H = I²Rt), a higher resistance produces more heat for the same current, which is the primary function of a heating device.
- High Melting Point: Alloys do not oxidise (or burn) easily and have very high melting points. This allows them to get red-hot and glow without melting or breaking, ensuring the appliance's durability and safety.
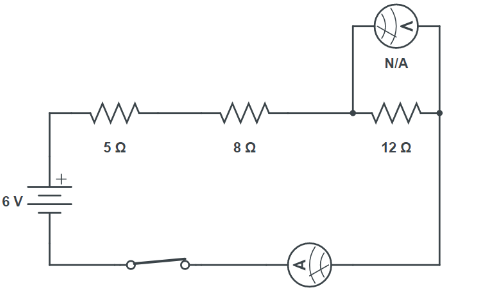
5. How should an ammeter and a voltmeter be connected in a circuit to correctly measure current and potential difference for a specific resistor?
To get accurate measurements in an electric circuit, the correct placement is crucial:
- Ammeter: An ammeter measures current and must always be connected in series with the component (e.g., a resistor) through which the current is to be measured. This ensures that the entire circuit current flows through it. An ideal ammeter has very low resistance.
- Voltmeter: A voltmeter measures potential difference (voltage) across a component and must always be connected in parallel to that component. This allows it to measure the voltage drop between the two points it is connected across. An ideal voltmeter has very high resistance.
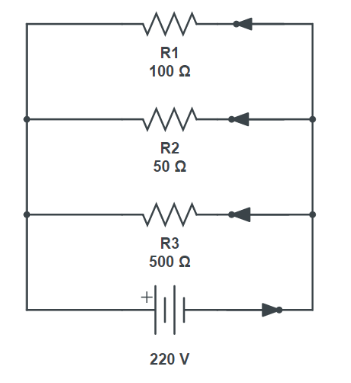
6. What are the key advantages of connecting electrical appliances in parallel at home, instead of in series?
Connecting domestic appliances in a parallel circuit is standard practice because of several significant advantages over a series connection:
- Same Voltage Supply: Every appliance in a parallel circuit receives the same voltage from the mains supply (e.g., 220 V in India), allowing each to operate at its rated power.
- Independent Operation: Each appliance can be turned on or off with its own switch without affecting the others. If one appliance fails, the rest of the circuit continues to function.
- Lower Overall Resistance: Adding more appliances in parallel decreases the total resistance of the circuit, allowing sufficient current to be drawn from the supply for all devices to work properly.
7. How do you solve for the equivalent resistance when resistors are connected in series versus in parallel?
The method to find the equivalent resistance (R_eq) depends on how the resistors are connected:
- For Resistors in Series: The total resistance is the sum of the individual resistances. The formula is: R_eq = R₁ + R₂ + R₃ + ... This means the total resistance is always greater than the largest individual resistance.
- For Resistors in Parallel: The reciprocal of the total resistance is the sum of the reciprocals of the individual resistances. The formula is: 1/R_eq = 1/R₁ + 1/R₂ + 1/R₃ + ... This means the total resistance is always less than the smallest individual resistance.
8. Why doesn't the connecting cord of an electric heater glow, while its heating element does, even though the same current flows through both?
This phenomenon is explained by Joule's law of heating (H ∝ R). Although the current is the same, the resistance of the two parts is very different:
- The heating element is made of an alloy like nichrome, which has a very high resistance. This causes a large amount of heat to be generated, making it glow red-hot.
- The connecting cord is made of a material like copper, which has very low resistance. Therefore, very little heat is generated in the cord, and it does not glow.
9. How can you use Ohm's Law to determine the different formulas for electric power, as explained in the NCERT solutions?
The basic formula for electric power (P) is P = V × I. By substituting Ohm's Law (V = I × R) into this basic formula, we can derive two other important expressions for power:
- To get power in terms of I and R: Replace V with (I × R) in the power formula. P = (I × R) × I. This gives P = I²R. This is useful when the current and resistance are known.
- To get power in terms of V and R: Rearrange Ohm's Law to I = V/R and substitute it into the power formula. P = V × (V/R). This gives P = V²/R. This is useful when voltage and resistance are known.
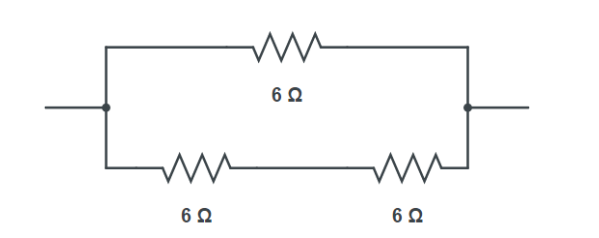
10. What is the correct method to find the highest and lowest total resistance that can be obtained from a given set of resistors?
To find the range of equivalent resistance from a combination of resistors, follow this simple rule:
- Highest Resistance: To achieve the maximum possible total resistance, you must connect all the given resistors in series. The equivalent resistance will be the sum of all individual resistances (R_eq = R₁ + R₂ + ...).
- Lowest Resistance: To achieve the minimum possible total resistance, you must connect all the given resistors in parallel. The equivalent resistance is found using the formula 1/R_eq = 1/R₁ + 1/R₂ + ..., and the result will be smaller than the smallest individual resistor in the set.
11. If a wire of resistance 'R' is cut into five equal parts which are then connected in parallel, why does the ratio R/R' equal 25?
This is a classic problem that demonstrates the relationship between length, resistance, and parallel combinations. Here is the step-by-step reasoning:
- Step 1: Resistance of each part. Since resistance is proportional to length, cutting the wire into five equal parts means the resistance of each new part becomes R/5.
- Step 2: Connecting in parallel. Now, these five resistors (each with resistance R/5) are connected in parallel. The formula for equivalent resistance (R') in parallel is 1/R' = 1/R₁ + 1/R₂ + 1/R₃ + 1/R₄ + 1/R₅.
- Step 3: Calculating R'. Substituting the value for each part: 1/R' = 1/(R/5) + 1/(R/5) + 1/(R/5) + 1/(R/5) + 1/(R/5). This simplifies to 1/R' = 5/R + 5/R + 5/R + 5/R + 5/R = 5 × (5/R) = 25/R.
- Step 4: Finding the ratio. If 1/R' = 25/R, then by cross-multiplication or inverting both sides, we get R' = R/25. Therefore, the ratio R/R' = 25.
12. What is the correct way to define the potential difference between two points as '1 Volt' for the CBSE Class 10 exam?
For the Class 10 CBSE exam, a precise definition is required. The potential difference between two points is defined as 1 Volt if 1 Joule of work is done in moving a charge of 1 Coulomb from one point to the other. This can be expressed using the formula V = W/Q, where V is potential difference, W is work done, and Q is charge. Therefore, 1 Volt = 1 Joule / 1 Coulomb.




















 Watch Video
Watch Video