NCERT Solutions For Class 10 Maths Chapter 3 Pair Of Linear Equations In Two Variables - 2025-26

Exercise 3.1: This exercise involves solving word problems by setting up a pair of linear equations. Students will need to translate word problems into mathematical equations and solve them to find the solution.

Exercise 3.2: This exercise covers the concept of cross-multiplication and its application in solving linear equations. Students will learn to solve equations using the cross-multiplication method and will also solve problems related to this topic.

Exercise 3.3: This exercise involves solving equations that are reducible to a pair of linear equations in two variables. Students will learn to reduce equations to linear form and solve them.

Access NCERT Solutions for Class 10 Maths Chapter 3 – Pair of Linear Equations in Two Variables

Exercise 3.1

1. Form the pair of linear equations in the following problems, and find their solutions graphically.

(i) \[\mathbf{10}\] students of \[\mathbf{Class}\text{ }\mathbf{X}\] took part in a Mathematics quiz. If the number of girls is \[\mathbf{4}\] more than the number of boys, find the number of boys and girls who took part in the quiz.

Ans (i): Assuming that the number of girls and boys be \[x\] and \[y\] respectively.

Writing the algebraic representation using the information given in the question-

\[x+y=10\]

\[x-y=4\]

Solution table for \[x+y=10\]-

\[x=10-y\]

Solution table for \[x-y=4\]-

\[x=4+y\]

Graphical representation-

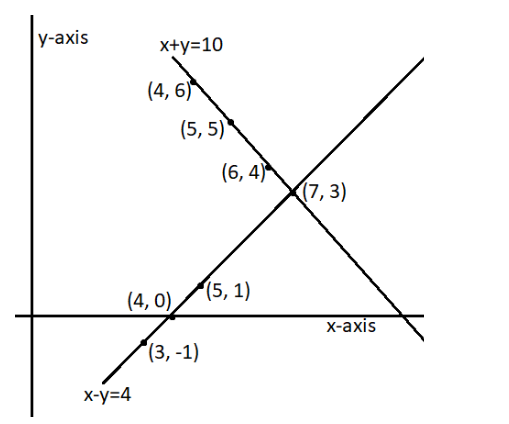
As we can see from the graph above, the point of intersection for the lines is \[\left( 7,3 \right)\]. Therefore, we can say that there are \[7\] girls and \[3\] boys in the class.

(ii) \[\mathbf{5}\] pencils and \[\mathbf{7}\] pens together cost \[\mathbf{Rs}\text{ }\mathbf{50}\], whereas \[\mathbf{7}\] pencils and \[\mathbf{5}\] pens together cost \[\mathbf{Rs}\text{ }\mathbf{46}\]. Find the cost of one pencil and that of one pen.

Ans (ii): Assuming that the cost of \[1\] pencil and \[1\] pen be \[x\] and \[y\] respectively.

Writing the algebraic representation using the information given in the question-

\[5x+7y=50\]

\[7x+5y=46\]

Solution table for \[5x+7y=50\]-

\[x=\frac{50-7y}{5}\]

Solution table for \[7x+5y=46\]-

\[x=\frac{46-5y}{7}\]

Graphical representation-

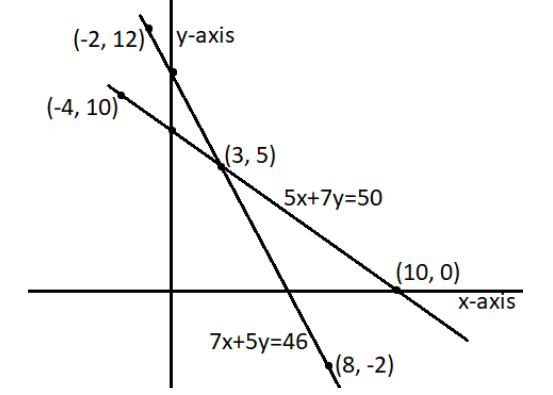
As we can see from the graph above, the point of intersection for the lines is \[\left( 3,5 \right)\]. Therefore, we can say that the cost of a pencil is \[Rs\text{ }3\] and the cost of a pen is \[Rs\text{ 5}\].

2. On comparing the ratios \[\frac{{{a}_{1}}}{{{a}_{2}}},\frac{{{b}_{1}}}{{{b}_{2}}}\] and \[\frac{{{c}_{1}}}{{{c}_{2}}}\], find out whether the lines representing the following pairs of linear equations at a point, are parallel or coincident-

(i) \[\mathbf{5x}-\mathbf{4y}+\mathbf{8}=\mathbf{0}\]

\[\mathbf{7x}+\mathbf{6y}-\mathbf{9}=\mathbf{0}\]

Ans: \[5x-4y+8=0\]

\[7x+6y-9=0\]

Calculating the values of \[{{a}_{1}},{{b}_{1}},{{c}_{1}},{{a}_{2}},{{b}_{2}}\] and \[{{c}_{2}}\] by comparing the above equations with \[{{a}_{1}}x+{{b}_{1}}y+{{c}_{1}}=0\] and \[{{a}_{2}}x+{{b}_{2}}y+{{c}_{2}}=0\],

\[{{a}_{1}}=5\], \[{{b}_{1}}=-4\], \[{{c}_{1}}=8\]

\[{{a}_{2}}=7\], \[{{b}_{2}}=6\], \[{{c}_{2}}=-9\]

\[\frac{{{a}_{1}}}{{{a}_{2}}}=\frac{5}{7}\]

\[\frac{{{b}_{1}}}{{{b}_{2}}}=\frac{-4}{6}=\frac{-2}{3}\]

Since \[\frac{{{a}_{1}}}{{{a}_{2}}}\ne \frac{{{b}_{1}}}{{{b}_{2}}}\].

Therefore, the given pair of equations have a unique solution, that is, the lines intersect at exactly one point.

(ii) \[\mathbf{9x}+\mathbf{3y}+\mathbf{12}=\mathbf{0}\]

\[\mathbf{18x}+\mathbf{6y}+\mathbf{24}=\mathbf{0}\]

Ans (ii): Calculating the values of \[{{a}_{1}},{{b}_{1}},{{c}_{1}},{{a}_{2}},{{b}_{2}}\] and \[{{c}_{2}}\] by comparing the above equations with \[{{a}_{1}}x+{{b}_{1}}y+{{c}_{1}}=0\] and \[{{a}_{2}}x+{{b}_{2}}y+{{c}_{2}}=0\],

\[{{a}_{1}}=9\], \[{{b}_{1}}=3\], \[{{c}_{1}}=12\]

\[{{a}_{2}}=18\], \[{{b}_{2}}=6\], \[{{c}_{2}}=24\]

\[\frac{{{a}_{1}}}{{{a}_{2}}}=\frac{1}{2}\]

\[\frac{{{b}_{1}}}{{{b}_{2}}}=\frac{1}{2}\]

\[\frac{{{c}_{1}}}{{{c}_{2}}}=\frac{1}{2}\]

Since \[\frac{{{a}_{1}}}{{{a}_{2}}}=\frac{{{b}_{1}}}{{{b}_{2}}}=\frac{{{c}_{1}}}{{{c}_{2}}}\].

Therefore, the lines representing the given pair of equations have infinite solutions as they are coincident.

(iii) \[\mathbf{6x}-\mathbf{3y}+\mathbf{10}=\mathbf{0}\]

\[\mathbf{2x}-\mathbf{y}+\mathbf{9}=\mathbf{0}\]

Ans (iii): Calculating the values of \[{{a}_{1}},{{b}_{1}},{{c}_{1}},{{a}_{2}},{{b}_{2}}\] and \[{{c}_{2}}\] by comparing the above equations with \[{{a}_{1}}x+{{b}_{1}}y+{{c}_{1}}=0\] and \[{{a}_{2}}x+{{b}_{2}}y+{{c}_{2}}=0\],

\[{{a}_{1}}=6\], \[{{b}_{1}}=-3\], \[{{c}_{1}}=10\]

\[{{a}_{2}}=2\], \[{{b}_{2}}=-1\], \[{{c}_{2}}=9\]

\[\frac{{{a}_{1}}}{{{a}_{2}}}=\frac{3}{1}\]

\[\frac{{{b}_{1}}}{{{b}_{2}}}=\frac{3}{1}\]

\[\frac{{{c}_{1}}}{{{c}_{2}}}=\frac{10}{9}\]

Since \[\frac{{{a}_{1}}}{{{a}_{2}}}=\frac{{{b}_{1}}}{{{b}_{2}}}\ne \frac{{{c}_{1}}}{{{c}_{2}}}\].

Therefore, the lines representing the given pair of equations have no solutions as they are parallel to each other.

3. On comparing the ratios \[\frac{{{a}_{1}}}{{{a}_{2}}},\frac{{{b}_{1}}}{{{b}_{2}}}\] and \[\frac{{{c}_{1}}}{{{c}_{2}}}\], find out whether the following pairs of linear equations are consistent, or inconsistent.

(i) \[3\mathbf{x}+2\mathbf{y}=5;2x-3y=7\]

Ans (i): For the given equations-

 \[\frac{{{a}_{1}}}{{{a}_{2}}}=\frac{3}{2}\]

\[\frac{{{b}_{1}}}{{{b}_{2}}}=\frac{-2}{3}\]

\[\frac{{{c}_{1}}}{{{c}_{2}}}=\frac{5}{7}\]

Since \[\frac{{{a}_{1}}}{{{a}_{2}}}\ne \frac{{{b}_{1}}}{{{b}_{2}}}\].

So, the given pair of equations have a unique solution, that is, the lines intersect at exactly one point. 

Therefore, the given pair of lines is consistent.

(ii) \[2x-3y=8;4\mathbf{x}-6\mathbf{y}=9\]

Ans (ii): For the given equations-

\[\frac{{{a}_{1}}}{{{a}_{2}}}=\frac{1}{2}\]

\[\frac{{{b}_{1}}}{{{b}_{2}}}=\frac{1}{2}\]

\[\frac{{{c}_{1}}}{{{c}_{2}}}=\frac{8}{9}\]

Since \[\frac{{{a}_{1}}}{{{a}_{2}}}=\frac{{{b}_{1}}}{{{b}_{2}}}\ne \frac{{{c}_{1}}}{{{c}_{2}}}\].

So, the lines representing the given pair of equations have no solutions as they are parallel to each other.

Therefore, the given pair of lines is inconsistent.

(iii) \[\frac{3}{2}x+\frac{5}{3}y=7;9\mathbf{x}-10\mathbf{y}=14\]

Ans (iii): For the given equations-

\[\frac{{{a}_{1}}}{{{a}_{2}}}=\frac{1}{6}\]

\[\frac{{{b}_{1}}}{{{b}_{2}}}=\frac{-1}{6}\]

\[\frac{{{c}_{1}}}{{{c}_{2}}}=\frac{1}{4}\]

Since \[\frac{{{a}_{1}}}{{{a}_{2}}}\ne \frac{{{b}_{1}}}{{{b}_{2}}}\].

So, the given pair of equations have a unique solution, that is, the lines intersect at exactly one point. 

Therefore, the given pair of lines is consistent.

(iv) \[5x-3y=11;-10\mathbf{x}+6\mathbf{y}=-22\]

Ans (iv): For the given equations-

\[\frac{{{a}_{1}}}{{{a}_{2}}}=\frac{-1}{2}\]

\[\frac{{{b}_{1}}}{{{b}_{2}}}=\frac{-1}{2}\]

\[\frac{{{c}_{1}}}{{{c}_{2}}}=\frac{-1}{2}\]

Since \[\frac{{{a}_{1}}}{{{a}_{2}}}=\frac{{{b}_{1}}}{{{b}_{2}}}=\frac{{{c}_{1}}}{{{c}_{2}}}\].

So, the lines representing the given pair of equations have infinite number of solutions as they are coincident.

Therefore, the given pair of lines is consistent.

(v) \[\frac{4}{3}x+2y=8;2\mathbf{x}+3\mathbf{y}=12\]

Ans (v): For the given equations-

\[\frac{{{a}_{1}}}{{{a}_{2}}}=\frac{2}{3}\]

\[\frac{{{b}_{1}}}{{{b}_{2}}}=\frac{2}{3}\]

\[\frac{{{c}_{1}}}{{{c}_{2}}}=\frac{2}{3}\]

Since \[\frac{{{a}_{1}}}{{{a}_{2}}}=\frac{{{b}_{1}}}{{{b}_{2}}}=\frac{{{c}_{1}}}{{{c}_{2}}}\].

So, the lines representing the given pair of equations have an infinite number of solutions as they are coincident.

Therefore, the given pair of lines is consistent.

4. Which of the following pairs of linear equations are consistent/ inconsistent? If consistent, obtain the solution graphically-

(i) \[x+y=5;2\mathbf{x}+2\mathbf{y}=10\]

Ans (i): For the given equations-

\[\frac{{{a}_{1}}}{{{a}_{2}}}=\frac{1}{2}\]

\[\frac{{{b}_{1}}}{{{b}_{2}}}=\frac{1}{2}\]

\[\frac{{{c}_{1}}}{{{c}_{2}}}=\frac{1}{2}\]

Since \[\frac{{{a}_{1}}}{{{a}_{2}}}=\frac{{{b}_{1}}}{{{b}_{2}}}=\frac{{{c}_{1}}}{{{c}_{2}}}\].

So, the lines representing the given pair of equations have infinite number of solutions as they are coincident.

Therefore, the given pair of lines is consistent.

Solution table for \[x+y=5\]-

\[x=5-y\]

Solution table for \[2x+2y=10\]-

\[x=\frac{10-2y}{2}\]

Graphical representation-

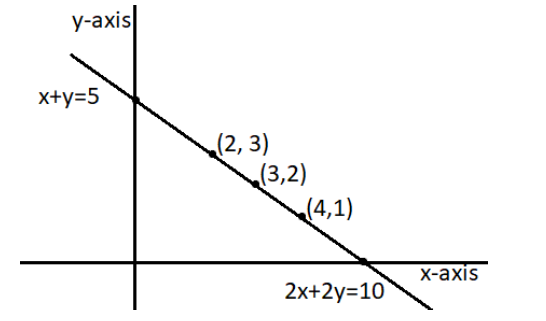
As shown in the graph above, the two lines are overlapping each other. Hence, they have infinite solutions.

(ii) \[x-y=8;3\mathbf{x}-3\mathbf{y}=16\]

Ans (ii): For the given equations-

\[\frac{{{a}_{1}}}{{{a}_{2}}}=\frac{1}{3}\]

\[\frac{{{b}_{1}}}{{{b}_{2}}}=\frac{1}{3}\]

\[\frac{{{c}_{1}}}{{{c}_{2}}}=\frac{1}{2}\]

Since \[\frac{{{a}_{1}}}{{{a}_{2}}}=\frac{{{b}_{1}}}{{{b}_{2}}}\ne \frac{{{c}_{1}}}{{{c}_{2}}}\].

So, the lines representing the given pair of equations have no solutions as they are parallel to each other.

Therefore, the given pair of lines is inconsistent.

(iii) \[2x+y-6=0;4\mathbf{x}-2\mathbf{y}-4=0\]

Ans (iii): For the given equations-

\[\frac{{{a}_{1}}}{{{a}_{2}}}=\frac{1}{2}\]

\[\frac{{{b}_{1}}}{{{b}_{2}}}=\frac{-1}{2}\]

\[\frac{{{c}_{1}}}{{{c}_{2}}}=\frac{3}{2}\]

Since \[\frac{{{a}_{1}}}{{{a}_{2}}}\ne \frac{{{b}_{1}}}{{{b}_{2}}}\].

So, the given pair of equations have a unique solution, that is, the lines intersect at exactly one point. 

Therefore, the given pair of lines is consistent.

Solution table for \[2x+y-6=0\]-

\[y=6-2x\]

Solution table for \[4x-2y-4=0\]-

\[y=\frac{4x-4}{2}\]

Graphical representation-

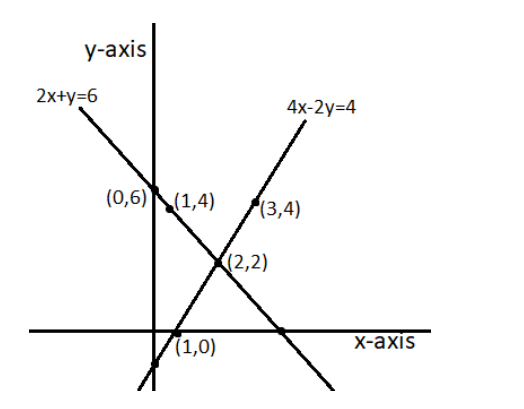
As shown in the graph above, the two lines intersect each other at only one point \[\left( 2,2 \right)\].

(iv) \[2x-2y-2=0;4\mathbf{x}-4\mathbf{y}-5=0\]

Ans (iv):  For the given equations-

\[\frac{{{a}_{1}}}{{{a}_{2}}}=\frac{1}{2}\]

\[\frac{{{b}_{1}}}{{{b}_{2}}}=\frac{1}{2}\]

\[\frac{{{c}_{1}}}{{{c}_{2}}}=\frac{2}{5}\]

Since \[\frac{{{a}_{1}}}{{{a}_{2}}}=\frac{{{b}_{1}}}{{{b}_{2}}}\ne \frac{{{c}_{1}}}{{{c}_{2}}}\].

So, the lines representing the given pair of equations have no solutions as they are parallel to each other.

Therefore, the given pair of lines is inconsistent.

5. Half the perimeter of a rectangular garden, whose length is \[\mathbf{4}\text{ }\mathbf{m}\] more than its width, is \[\mathbf{36}\text{ }\mathbf{m}\]. Find the dimensions of the garden.

Ans: Assuming that the width and length of the garden be \[x\] and \[y\] respectively.

Writing the algebraic representation using the information given in the question-

\[y-x=4\]

\[x+y=36\]

Solution table for \[y-x=4\]-

\[y=x+4\]

Solution table for \[x+y=36\]-

\[y=36-x\]

Graphical representation-

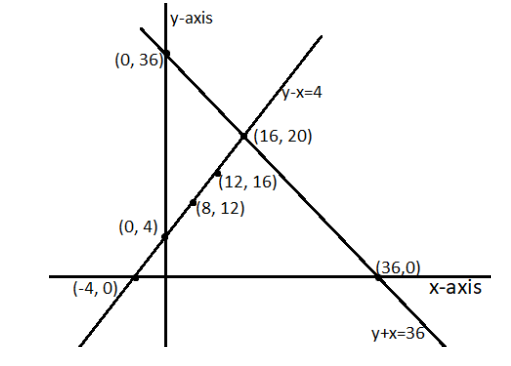
As shown in the graph above, the two lines intersect each other at only one point \[\left( 16,20 \right)\]. Therefore the length of the garden is \[20\text{ }m\] and its breadth is \[\text{16 }m\].

6. Given the linear equation \[\mathbf{2x}+\mathbf{3y}-\mathbf{8}=\mathbf{0}\], write another linear equations in two variables such that the geometrical representation of the pair so formed is-

(i) Intersecting lines

Ans (i): If two lines are intersecting then-

\[\frac{{{a}_{1}}}{{{a}_{2}}}\ne \frac{{{b}_{1}}}{{{b}_{2}}}\]

So, taking the second line as \[2x+4y-6=0\],

Now, 

\[\frac{{{a}_{1}}}{{{a}_{2}}}=1\]

\[\frac{{{b}_{1}}}{{{b}_{2}}}=\frac{3}{4}\]

As \[\frac{{{a}_{1}}}{{{a}_{2}}}\ne \frac{{{b}_{1}}}{{{b}_{2}}}\], the two lines are interesting each other.

(ii) Parallel lines

Ans: If two lines are intersecting then-

\[\frac{{{a}_{1}}}{{{a}_{2}}}=\frac{{{b}_{1}}}{{{b}_{2}}}\ne \frac{{{c}_{1}}}{{{c}_{2}}}\]

So, taking the second line as \[4x+6y-8=0\],

Now, 

\[\frac{{{a}_{1}}}{{{a}_{2}}}=\frac{1}{2}\]

\[\frac{{{b}_{1}}}{{{b}_{2}}}=\frac{1}{2}\]

\[\frac{{{c}_{1}}}{{{c}_{2}}}=1\]

As \[\frac{{{a}_{1}}}{{{a}_{2}}}=\frac{{{b}_{1}}}{{{b}_{2}}}\ne \frac{{{c}_{1}}}{{{c}_{2}}}\], the two lines are parallel to each other.

(iii) Coincident lines

Ans: If two lines are intersecting then-

\[\frac{{{a}_{1}}}{{{a}_{2}}}=\frac{{{b}_{1}}}{{{b}_{2}}}=\frac{{{c}_{1}}}{{{c}_{2}}}\]

So, taking the second line as \[6x+9y-24=0\],

Now, 

\[\frac{{{a}_{1}}}{{{a}_{2}}}=\frac{1}{3}\]

\[\frac{{{b}_{1}}}{{{b}_{2}}}=\frac{1}{3}\]

\[\frac{{{c}_{1}}}{{{c}_{2}}}=\frac{1}{3}\]

As \[\frac{{{a}_{1}}}{{{a}_{2}}}=\frac{{{b}_{1}}}{{{b}_{2}}}=\frac{{{c}_{1}}}{{{c}_{2}}}\], the two lines are coincident.

7. Draw the graphs of the equations \[\mathbf{x}-\mathbf{y}+\mathbf{1}=\mathbf{0}\] and \[\mathbf{3x}+\mathbf{2y}-\mathbf{12}=\mathbf{0}\]. Determine the coordinates of the vertices of the triangle formed by these lines and the \[x-axis\], and shade the triangular region.

Ans: Solution table for \[x-y+1=0\]-

\[x=y-1\]

Solution table for \[3x+2y-12=0\]-

\[x=\frac{12-2y}{3}\]

Graphical representation-

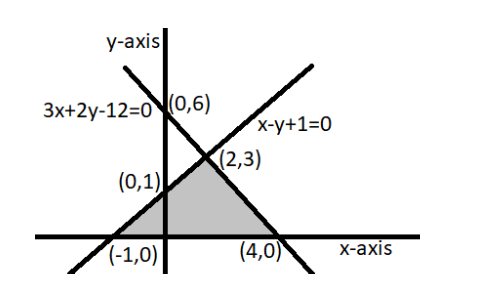
As shown in the graph above, the lines are intersecting each other at point \[\left( 2,3 \right)\] and \[x-axis\] at \[\left( -1,0 \right)\] and \[\left( 4,0 \right)\]. So the obtained triangle has vertices \[\left( 2,3 \right)\], \[\left( -1,0 \right)\] and \[\left( 4,0 \right)\].

Exercise 3.2

1. Solve the following pair of linear equations by the substitution method.

(i) \[x+y=14;x-y=4\]

Ans (i): The given equations are-

\[x+y=14\]           …… (i)

\[x-y=4\]             …… (ii)

From equation (i)-

\[x=14-y\]          …… (iii)

Substituting (iii) in equation (ii), we get

\[\left( 14-y \right)-y=4\]

\[14-2y=4\]

\[10=2y\]

\[y=5\]                  …… (iv)

Substituting (iv) in (iii), we get

\[x=9\]

Therefore, \[x=9\] and \[y=5\].

(ii) \[s-t=3;\frac{s}{3}+\frac{t}{2}=6\]

Ans (ii): The given equations are-

\[s-t=3\]           …… (i)

\[\frac{s}{3}+\frac{t}{2}=6\]       …… (ii)

From equation (i)-

\[s=t+3\]          …… (iii)

Substituting (iii) in equation (ii), we get

\[\frac{t+3}{3}+\frac{t}{2}=6\]

\[2t+6+3t=36\]

\[5t=30\]

\[t=6\]                  …… (iv)

Substituting (iv) in (iii), we get

\[s=9\]

Therefore, \[s=9\] and \[t=6\].

(iii) \[3x-y=3;9x-3y=9\]

Ans (iii): The given equations are-

\[3x-y=3\]           …… (i)

\[9x-3y=9\]             …… (ii)

From equation (i)-

\[y=3x-3\]          …… (iii)

Substituting (iii) in equation (ii), we get

\[9x-3\left( 3x-3 \right)=9\]

\[9x-9x+9=9\]

\[9=9\]

For all \[x\] and \[y\].

Therefore, the given equations have infinite solutions. One of the solution is \[x=1,y=0\].

(iv) \[0.2x-0.3y=1.3;0.4x+0.5y=2.3\]

Ans (iv): The given equations are-

\[0.2x-0.3y=1.3\]           …… (i)

\[0.4x+0.5y=2.3\]             …… (ii)

From equation (i)-

\[x=\frac{1.3-0.3y}{0.2}\]          …… (iii)

Substituting (iii) in equation (ii), we get

\[0.4\left( \frac{1.3-0.3y}{0.2} \right)-0.5y=2.3\]

\[2.6-0.6y+0.5y=2.3\]

\[2.6-2.3=0.1y\]

\[y=3\]                  …… (iv)

Substituting (iv) in (iii), we get

\[x=\frac{1.3-0.3\left( 3 \right)}{0.2}\]

\[x=2\]

Therefore, \[x=2\] and \[y=3\].

(v) \[\sqrt{2}x-\sqrt{3}y=0;\sqrt{3}x-\sqrt{8}y=0\]

Ans (v): The given equations are-

\[\sqrt{2}x-\sqrt{3}y=0\]           …… (i)

\[\sqrt{3}x-\sqrt{8}y=0\]             …… (ii)

From equation (i)-

\[x=\frac{-\sqrt{3}y}{\sqrt{2}}\]          …… (iii)

Substituting (iii) in equation (ii), we get

\[\sqrt{3}\left( \frac{-\sqrt{3}y}{\sqrt{2}} \right)-\sqrt{8}y=0\]

\[\frac{-\sqrt{3}y}{\sqrt{2}}-2\sqrt{2}y=0\]

\[y\left( \frac{-\sqrt{3}}{\sqrt{2}}-2\sqrt{2} \right)=0\]

\[y=0\]                  …… (iv)

Substituting (iv) in (iii), we get

\[x=0\]

Therefore, \[x=0\] and \[y=0\].

(vi) \[\frac{3x}{2}-\frac{5y}{3}=-2;\frac{x}{3}+\frac{y}{2}=\frac{13}{6}\]

Ans (vi): The given equations are-

\[\frac{3x}{2}-\frac{5y}{3}=-2\]           …… (i)

\[\frac{x}{3}+\frac{y}{2}=\frac{13}{6}\]             …… (ii)

From equation (i)-

\[x=\frac{-12+10y}{9}\]          …… (iii)

Substituting (iii) in equation (ii), we get

\[\frac{\left( \frac{-12+10y}{9} \right)}{3}+\frac{y}{2}=\frac{13}{6}\]

\[\frac{-12+10y}{27}+\frac{y}{2}=\frac{13}{6}\]

\[\frac{-24+20y+27y}{54}=\frac{13}{6}\]

\[47y=141\]

\[y=3\]                  …… (iv)

Substituting (iv) in (iii), we get

\[x=2\]

Therefore, \[x=0\] and \[y=3\].

2. Solve \[\mathbf{2x}+\mathbf{3y}=\mathbf{11}\] and \[\mathbf{2x}-\mathbf{4y}=-\mathbf{24}\] and hence find the value of ‘\[m\]’ for which \[\mathbf{y}=\mathbf{mx}+\mathbf{3}\].

Ans: The given equations are-

\[2x+3y=11\]           …… (i)

\[2x-4y=-24\]             …… (ii)

From equation (i)-

\[x=\frac{11-3y}{2}\]          …… (iii)

Substituting (iii) in equation (ii), we get

\[2\left( \frac{11-3y}{2} \right)-4y=-24\]

\[11-3y-4y=-24\]

\[-7y=-35\]

\[y=5\]                  …… (iv)

Substituting (iv) in (iii), we get

\[x=-2\]

Therefore, \[x=-2\] and \[y=5\].

Calculating the value of \[m\]-

\[y=mx+3\]

\[5=-2m+3\]

\[m=-1\]

3. Form the pair of linear equations for the following problems and find their solution by substitution method.

(i) The difference between two numbers is \[\mathbf{26}\] and one number is three times the other. Find them.

Ans (i): Assuming one number be \[x\] and another number be \[y\] such that \[y>x\],

Writing the algebraic representation using the information given in the question-

\[y=3x\]             …… (i)

\[y-x=26\]    …… (ii)

Substituting the value of \[y\] from equation (i) in equation (ii), we get

\[3x-x=26\]

\[2x=26\]

\[x=13\]                  …… (iii)

Substituting (iii) in (i), we get

\[y=39\]

Therefore, \[x=13\] and \[y=39\].

(ii) The larger of two supplementary angles exceeds the smaller by \[\mathbf{18}\] degrees. Find them.

Ans (ii): Assuming the larger angle be \[x\] and smaller angle be \[y\]. 

The sum of a pair of supplementary angles is always \[{{180}^{\circ }}\].

Writing the algebraic representation using the information given in the question-

\[x+y=180\]             …… (i)

\[x-y=18\]    …… (ii)

Substituting the value of \[x\] from equation (i) in equation (ii), we get

\[180-y-y=18\]

\[162=2y\]

\[y=81\]                  …… (iii)

Substituting (iii) in (i), we get

\[x=99\]

Therefore, the two angles are  \[x={{99}^{\circ }}\] and \[y={{81}^{\circ }}\].

(iii) The coach of a cricket team buys \[\mathbf{7}\] bats and 6 balls for \[\mathbf{Rs}\text{ }\mathbf{3800}\]. Later, she buys \[\mathbf{3}\] bats and \[\mathbf{5}\] balls for \[\mathbf{Rs}\text{ }\mathbf{1750}\]. Find the cost of each bat and each ball.

Ans (iii): Assuming the cost of a bat is \[x\] and the cost of a ball is \[y\].

Writing the algebraic representation using the information given in the question-

\[7x+6y=3800\]             …… (i)

\[3x+5y=1750\]    …… (ii)

From equation (i)-

\[y=\frac{3800-7x}{6}\]       …… (iii)

Substituting (iii) in equation (ii)- 

\[3x+5\left( \frac{3800-7x}{6} \right)=1750\]

\[3x+\frac{9500}{3}-\frac{35x}{6}=1750\]

\[3x-\frac{35x}{6}=1750-\frac{9500}{3}\]

\[\frac{18x-35x}{6}=\frac{5250-9500}{3}\]

\[\frac{17x}{6}=\frac{-4250}{3}\]

\[x=500\]                  …… (iv)

Substituting (iv) in (iii), we get

\[y=\frac{3800-7\left( 500 \right)}{6}\]

\[y=50\]

Therefore, the bat costs \[Rs\text{ }500\] and the ball costs \[Rs\text{ }50\].

(iv) The taxi charges in a city consist of a fixed charge together with the charge for the distance covered. For a distance of \[\mathbf{10}\text{ }\mathbf{km}\], the charge paid is \[\mathbf{Rs}\text{ }\mathbf{105}\] and for a journey of \[\mathbf{15}\text{ }\mathbf{km}\], the charge paid is \[\mathbf{Rs}\text{ }\mathbf{155}\]. What are the fixed charges and the charge per km? How much does a person have to pay for travelling a distance of \[\mathbf{25}\text{ }\mathbf{km}\].

Ans (iv): Assuming the fixed charge be \[Rs\text{ }x\] and the per km charge be \[Rs\text{ y}\].

Writing the algebraic representation using the information given in the question-

\[x+10y=105\]             …… (i)

\[x+15y=155\]    …… (ii)

From equation (i)-

\[x=105-10y\]       …… (iii)

Substituting (iii) in equation (ii)- 

\[105-10y+15y=155\]

\[5y=50\]

\[y=10\]                  …… (iv)

Substituting (iv) in (iii), we get

\[x=105-10\left( 10 \right)\]

\[x=5\]

Therefore, the fixed charge is \[Rs\text{ }5\] and the per km charge is \[Rs\text{ 10}\].

So, charge for \[25\text{ }km\] will be-

\[=Rs\text{ }\left( x+25y \right)\]

\[=Rs\text{ 255}\]

(v) A fraction becomes \[\frac{9}{11}\], if \[\mathbf{2}\] is added to both the numerator and the denominator. If, \[\mathbf{3}\] is added to both the numerator and the denominator it becomes \[\frac{5}{6}\]. Find the fraction.

Ans (v): Assuming the fraction be \[\frac{x}{y}\].

Writing the algebraic representation using the information given in the question-

\[\frac{x+2}{y+2}=\frac{9}{11}\]

\[11x+22=9y+18\]

\[11x-9y=-4\]             …… (i)

\[\frac{x+3}{y+3}=\frac{5}{6}\]

\[6x+18=5y+15\]

\[6x-5y=-3\]    …… (ii)

From equation (i)-

\[x=\frac{-4+9y}{11}\]       …… (iii)

Substituting (iii) in equation (ii)- 

\[6\left( \frac{-4+9y}{11} \right)-5y=-3\]

\[-24+54y-55y=-33\]

\[y=9\]                  …… (iv)

Substituting (iv) in (iii), we get

\[x=\frac{-4+9\left( 9 \right)}{11}\]

\[x=7\]

Therefore, the fraction is \[\frac{7}{9}\].

(vi) Five years hence, the age of Jacob will be three times that of his son. Five years ago, Jacob’s age was seven times that of his son. What are their present ages?

Ans (vi): Assuming the age of Jacob be \[x\] and the age of his son be \[y\].

Writing the algebraic representation using the information given in the .question-

\[\left( x+5 \right)=3\left( y+5 \right)\]

\[x-3y=10\]             …… (i)

\[\left( x-5 \right)=7\left( y-5 \right)\]

\[x-7y=-30\]    …… (ii)

From equation (i)-

\[x=3y+10\]       …… (iii)

Substituting (iii) in equation (ii)- 

\[3y+10-7y=-30\]

\[-4y=-40\]

\[y=10\]                  …… (iv)

Substituting (iv) in (iii), we get

\[x=3\left( 10 \right)+10\]

\[x=40\]

Therefore, Jacob’s present age is \[40\] years and his son’s present age is \[10\] years.

Exercise 3.3

1. Solve the following pair of linear equations by the elimination method and the substitution method-

(i) \[\mathbf{x}+\mathbf{y}=\mathbf{5}\] and \[\mathbf{2x}\mathbf{3y}=\mathbf{4}\] 

Ans (i): 

Elimination method

The given equations are-

\[x+y=5\]          …… (i)

\[2x-3y=4\]   …… (ii)

Multiplying equation (ii) by \[2\], we get

\[2x+2y=10\]   …… (iii)

Subtracting equation (ii) from equation (iii), we obtain

\[5y=6\]

\[y=\frac{6}{5}\]              …… (iv)

Substituting the value of (iv) in equation (i), we get

\[x=5-\frac{6}{5}\]

\[x=\frac{19}{5}\]

Therefore, \[x=\frac{19}{5}\] and \[y=\frac{6}{5}\].

Substitution method-

From equation (i) we get

\[x=5-y\]      …… (v)

Substituting (v) in equation (ii), we get

\[2\left( 5-y \right)-3y=4\]

\[-5y=-6\]

\[y=\frac{6}{5}\]            …… (vi)

Substituting (vi) in equation (v), we obtain

\[x=5-\frac{6}{5}\]

\[x=\frac{19}{5}\]

Therefore, \[x=\frac{19}{5}\] and \[y=\frac{6}{5}\].

(ii) \[\mathbf{3x}+\mathbf{4y}=\mathbf{10}\] and \[\mathbf{2x}\mathbf{2y}=\mathbf{2}\]

Ans (ii): Elimination method

The given equations are-

\[3x+4y=10\]          …… (i)

\[2x-2y=2\]   …… (ii)

Multiplying equation (ii) by \[2\], we get

\[4x-4y=4\]   …… (iii)

Adding equation (ii) and (iii), we obtain

\[7x=14\]

\[x=2\]              …… (iv)

Substituting the value of (iv) in equation (i), we get

\[6+4y=10\]

\[4y=4\]

\[y=1\]

Therefore, \[x=2\] and \[y=1\].

Substitution method-

From equation (ii) we get

\[x=1+y\]      …… (v)

Substituting (v) in equation (i), we get

\[3\left( 1+y \right)+4y=10\]

\[7y=7\]

\[y=1\]            …… (vi)

Substituting (vi) in equation (v), we obtain

\[x=1+1\]

\[x=2\]

Therefore, \[x=2\] and \[y=1\].

(iii) \[\mathbf{3x}\mathbf{5y}\mathbf{4}=\mathbf{0}\] and \[\mathbf{9x}=\mathbf{2y}+\mathbf{7}\]

Ans (iii): Elimination method

The given equations are-

\[3x-5y-4=0\]          …… (i)

\[9x=2y+7\]

\[9x-2y=7\]   …… (ii)

Multiplying equation (i) by \[3\], we get

\[9x-15y-12=0\]   …… (iii)

Subtracting equation (iii) from equation (ii), we obtain

\[13y=-5\]

\[y=-\frac{5}{13}\]              …… (iv)

Substituting the value of (iv) in equation (i), we get

\[3x+\frac{25}{13}-4=0\]

\[3x=\frac{27}{13}\]

\[x=\frac{9}{13}\]

Therefore, \[x=\frac{9}{13}\] and \[y=-\frac{5}{13}\].

Substitution method-

From equation (i) we get

\[x=\frac{5y+4}{3}\]      …… (v)

Substituting (v) in equation (ii), we get

\[9\left( \frac{5y+4}{3} \right)-2y-7=0\]

\[13y=-5\]

\[y=\frac{-5}{13}\]            …… (vi)

Substituting (vi) in equation (v), we obtain

\[x=\frac{5\left( \frac{-5}{13} \right)+4}{3}\]

\[x=\frac{9}{13}\]

Therefore, \[x=\frac{9}{13}\] and \[y=\frac{-5}{13}\].

(iv) \[\frac{x}{2}+\frac{2y}{3}=-1\] and \[x-\frac{y}{3}=3\]

Ans (iv): Elimination method

The given equations are-

\[\frac{x}{2}+\frac{2y}{3}=-1\]

\[3x+4y=-6\]          …… (i)

\[x-\frac{y}{3}=3\]

\[3x-y=9\]   …… (ii)

Subtracting equation (ii) from equation (i), we obtain

\[5y=-15\]

\[y=-3\]              …… (iv)

Substituting the value of (iv) in equation (i), we get

\[3x+4\left( -3 \right)=-6\]

\[3x=6\]

\[x=2\]

Therefore, \[x=2\] and \[y=-3\].

Substitution method-

From equation (ii) we get

\[x=\frac{y+9}{3}\]      …… (v)

Substituting (v) in equation (i), we get

\[3\left( \frac{y+9}{3} \right)+4y=-6\]

\[5y=-15\]

\[y=-3\]            …… (vi)

Substituting (vi) in equation (v), we obtain

\[x=\frac{-3+9}{3}\]

\[x=2\]

Therefore, \[x=2\] and \[y=-3\].

2. Form the pair of linear equations in the following problems, and find their solutions (if they exist) by the elimination method-

(i) If we add \[\mathbf{1}\] to the numerator and subtract \[\mathbf{1}\] from the denominator, a fraction reduces to \[\mathbf{1}\]. It becomes \[\frac{\mathbf{1}}{2}\] if we only add \[\mathbf{1}\] to the denominator. What is the fraction?

Ans (i): Assuming the fraction be \[\frac{x}{y}\].

Writing the algebraic representation using the information given in the question-

\[\frac{x+1}{y-1}=1\]

\[x-y=-2\]             …… (i)

\[\frac{x}{y+1}=1\]

\[2x-y=1\]    …… (ii)

Subtracting equation (i) from equation (ii), we obtain

\[x=3\]              …… (iii)

Substituting the value of (iii) in equation (i), we get

\[3-y=-2\]

\[y=5\]

Therefore, \[x=2\] and \[y=-3\].

Hence the fraction is \[\frac{3}{5}\].

(ii) Five years ago, Nuri was thrice as old as Sonu. Ten years later, Nuri will be twice as old as Sonu. How old are Nuri and Sonu?

Ans (ii): Assuming the present age of Nuri be \[x\] and present age of Sonu be \[y\].

Writing the algebraic representation using the information given in the question-

\[\left( x-5 \right)=3\left( y-5 \right)\]

\[x-3y=-10\]             …… (i)

\[\left( x+10 \right)=2\left( y+10 \right)\]

\[x-2y=10\]    …… (ii)

Subtracting equation (i) from equation (ii), we obtain

\[y=20\]              …… (iii)

Substituting the value of (iii) in equation (i), we get

\[x-60=-10\]

\[x=50\]

Therefore, \[x=50\] and \[y=20\].

Hence Nuri’s present age is \[50\] years and Sonu’s present age is \[20\] years.

(iii) The sum of the digits of a two-digit number is \[\mathbf{9}\]. Also, nine times this number is twice the number obtained by reversing the order of the digits. Find the number.

Ans (iii): Assuming the unit digit of the number be \[x\] and the tens digit be \[y\].

Therefore, the number is \[10y+x\]

The number after reversing the digits is \[10x+y\].

Writing the algebraic representation using the information given in the question-

\[x+y=9\]             …… (i)

\[9\left( 10y+x \right)=2\left( 10x+y \right)\]

\[-x+8y=0\]    …… (ii)

Adding equation (i) and (ii), we obtain

\[9y=9\]

\[y=1\]              …… (iii)

Substituting the value of (iii) in equation (i), we get

\[x=8\]

Therefore, \[x=8\] and \[y=1\].

Hence the number is \[10y+x=18\].

(iv) Meena went to bank to withdraw \[\mathbf{Rs}\text{ }\mathbf{2000}\]. She asked the cashier to give her \[\mathbf{Rs}\text{ }\mathbf{50}\] and \[\mathbf{Rs}\text{ }\mathbf{100}\] notes only. Meena got \[\mathbf{25}\] notes in all. Find how many notes of \[\mathbf{Rs}\text{ }\mathbf{50}\] and \[\mathbf{Rs}\text{ }\mathbf{100}\] she received.

Ans (iv): Assuming the number of \[Rs\text{ }50\] notes be \[x\] and the number of \[Rs\text{ }100\] be \[y\].

Writing the algebraic representation using the information given in the question-

\[x+y=25\]             …… (i)

\[50x+100y=2000\]    …… (ii)

Multiplying equation (i) by \[50\], we obtain

\[50x+50y=1250\]     …… (iii)

Subtracting equation (iii) from equation (ii), we obtain

\[50y=750\]

\[y=15\]              …… (iv)

Substituting the value of (iv) in equation (i), we get

\[x=10\]

Therefore, \[x=10\] and \[y=15\].

Hence Meena has \[10\] notes of \[Rs\text{ }50\] and \[15\] notes of \[Rs\text{ }100\].

(v) A lending library has a fixed charge for the first three days and an additional charge for each day thereafter. Saritha paid \[\mathbf{Rs}\text{ }\mathbf{27}\] for a book kept for seven days, while Susy paid \[\mathbf{Rs}\text{ }\mathbf{21}\] for the book she kept for five days. Find the fixed charge and the charge for each extra day.

Ans (v): Assuming that the charge for first three days is \[Rs\text{ }x\] and the charge for each day thereafter is \[Rs\text{ y}\].

Writing the algebraic representation using the information given in the question-

\[x+4y=27\]             …… (i)

\[x+2y=21\]    …… (ii)

Subtracting equation (ii) from equation (i), we obtain

\[2y=6\]

\[y=3\]     …… (iii)

Subtracting equation (iii) from equation (i), we obtain

\[x+12=27\]

\[x=15\]              …… (iv)

Therefore, \[x=15\] and \[y=3\].

Hence, fixed charges are \[Rs\text{ 15}\] and charges per day are \[Rs\text{ 3}\].

Also You Can Find the Solutions of All the Maths Chapters Below.

3. Introduction

A Linear Equation is an equation of straight line. It is in the form of ax + by + c = 0 where a, b and c are the real numbers (a≠0 and b≠0) and x and y are the two variables,

Here a and b are the coefficients and c is the constant of the equation.

3.1 Importance

The key points that state why there is a need for NCERT solutions of chapter 3 maths class 10 are:

• Our subject experts have prepared these solutions in a detailed step-wise manner.

• All the important concepts of this chapter are covered in these solutions.

• Every sum given in the exercises is solved in a self-explanatory manner so that students can prepare effectively for the exams.

3.2 Pair of Linear Equations

Two Linear Equations having two same variables are known as the pair of Linear Equations in two variables. A linear equation in two variables involves variables x and y, and is expressed as ax + by + c = 0, where a, b, and c are real numbers (a and b ≠ 0).

• a1x + b1y + c1 = 0

• a2x + b2y + c2 = 0

3.3 Graphical Method of Solution of a Pair of Linear Equations

1. When two lines intersect each other at only one point, then we conclude that there is one and only one solution. It means that a unique solution exists for this pair of linear equations in two variables. This type of pair of linear equations is called a consistent pair of Linear equations. 

2. If the two lines are coincident, we can say that the pair of linear equations will have infinitely many solutions. This type of pair of linear equations can be called an inconsistent pair of Linear equations. 

3. If the two lines are parallel to each other, which means they do not meet at all, then we can say that the two linear equations will not have any common solution. This type of pair of linear equations will be called the dependent pair of Linear equations. 

3.4 Algebraic Methods of Solving a Pair of Linear Equations

The solution of a pair of linear equations is of the form (x,y), and it satisfies both equations at the same time. Using following methods, we can find the solution to a consistent pair of linear equations:

3.4.1 Substitution Method:

(a) Use one equation to find the value of a single variable, such as y in terms of x or x in terms of y.

(b) To get the equation in one variable and determine the solution, substitute this value in the second equation.

(c) Now, change the value or solution that was found in step (b) to the one found in step (a) of the equation.

3.4.2 Elimination Method:

(a) To make the coefficient of any one variable numerically equal, multiply both equations by appropriate non-zero constants if the coefficient of any one variable differs in either one.

(b) Solve the equations in one variable by adding or subtracting the ones that were so obtained.

(c) To obtain the value of the second variable, now substitute the value of the variable obtained in the previous step into either of the original equations.

3.4.3 Cross-multiplication Method:

The two linear equations in two variables are as follows: 

$a_1x + b_1y + c_1 = 0$

$a_2x + b_2y + c_2 = 0$

Take a look at the diagram below.

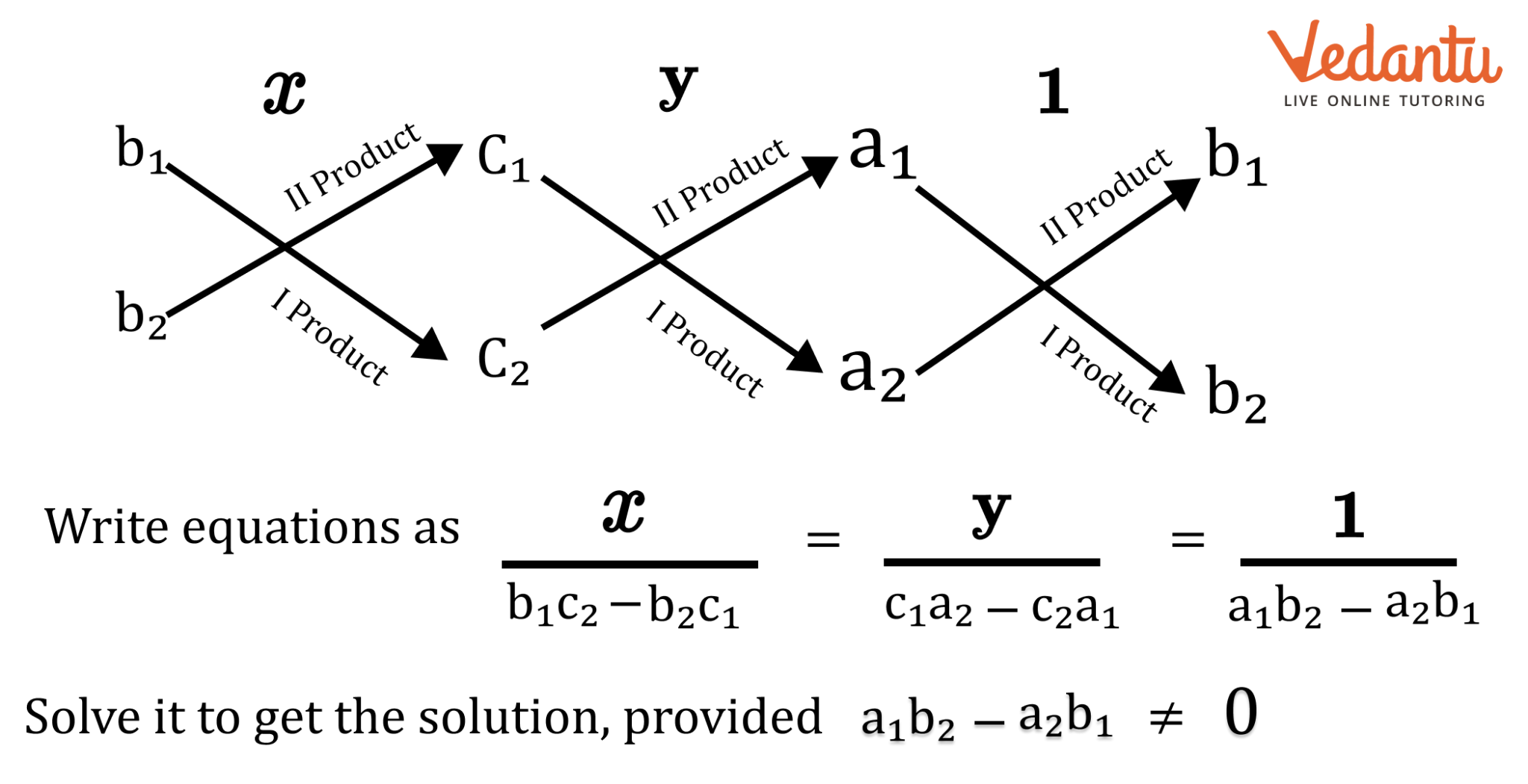
Determine the solution by solving it, given that $a_1b_2 - a_2b_1 \neq 0$.

3.5 Solving Word Problems:

1. Carefully read the problem and identify the unknown quantities. Give these unknown quantities: x, y, r, s, t, and so on.

2. Find the variables that must be determined.

3. Carefully read the problem and transform the equations into terms of the variables to be determined.

4. Solve the equations using any of the three methods listed above.

3.6 Equations Reducible to a Pair of Linear Equations in Two Variables

Sometimes pairs of equations are not linear (or not in standard form), then they are altered so that they reduce to a pair of linear equations in standard form.
For example

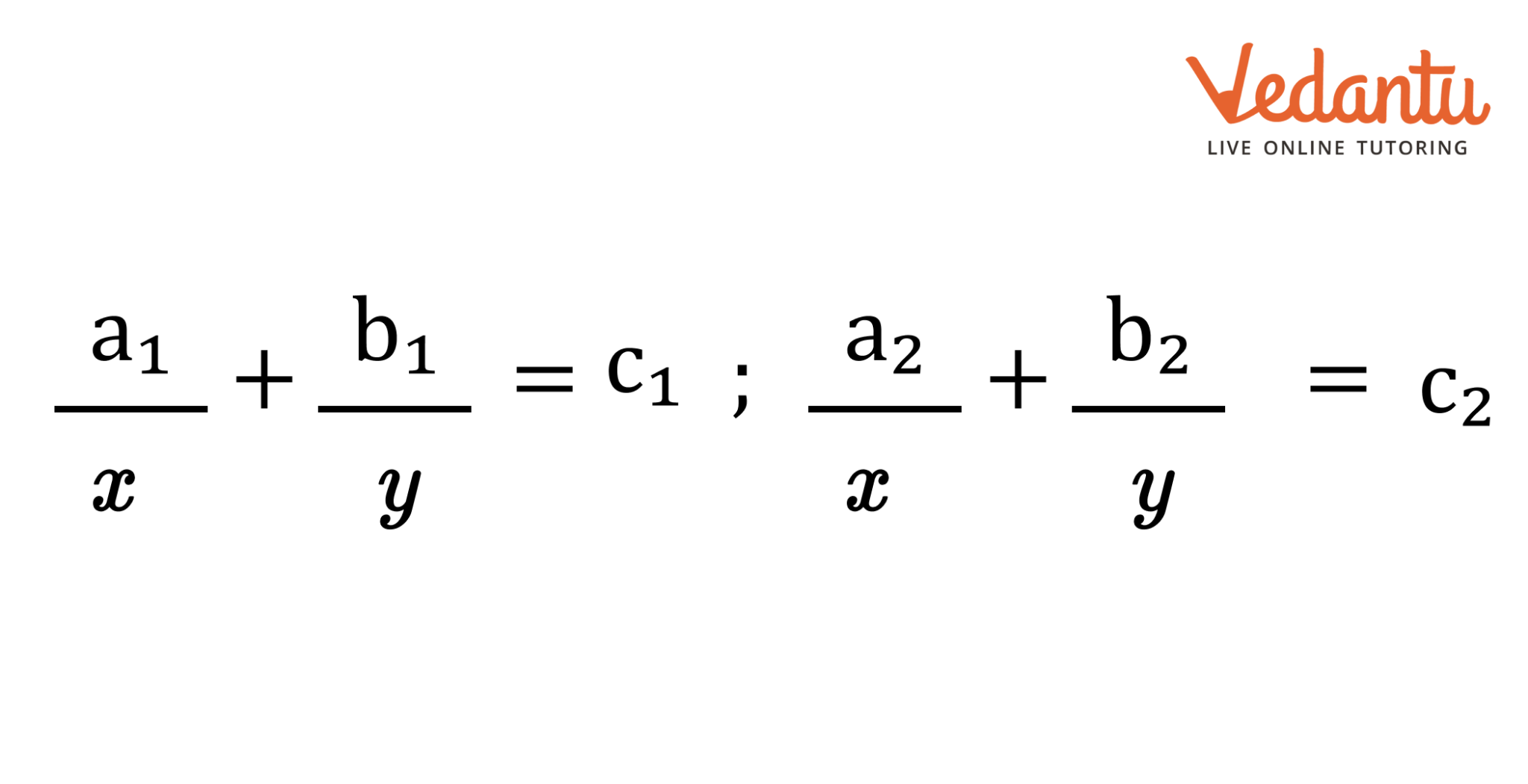
Here we substitute $\dfrac{1}{x} = p$ & $\dfrac{1}{y} = q$, the above equations reduces to:
$a_1p + b_1q = c_1$ ; $a_2p - b_2q = c_2$
Now we can use any method to solve them.

Summary of Pair of Linear Equations in Two Variables

The main ideas that should be committed to memory in order to answer the practice questions in the chapter Pair of Linear Equations in Two Variables are included in the Summary section. You can review every idea covered in this chapter by referring to the points in this section.

• A pair of linear equations in two variables is defined as two linear equations in the same two variables. Both a graphic and an algebraic representation are possible for the pair of linear equations in two variables. Two lines can be used to depict the graph:

• A pair of equations is considered consistent if and only if the lines cross at that moment.

• The two equations are dependent if the lines coincide.

• The two equations are inconsistent if the lines are parallel to one another.

The two linear equations in two variables can be solved algebraically using the following techniques:

• Substitution Method

• Elimination Method

• Cross-multiplication Method

Overview of Deleted Syllabus for CBSE Class 10 Maths Chapter - 3

Class 10 Maths Chapter 3: Exercise Breakdown

Conclusion

The NCERT Solutions for Class 10 Maths Chapter 3 - Pair Of Linear Equations In Two Variables provided by Vedantu offer comprehensive explanations to tackle problems effectively. It's crucial to grasp the concept of linear equations and their graphical representation. Focus on understanding the methods like substitution and elimination for solving pairs of linear equations. Previous year question papers usually include around 6-8 questions from this chapter. Practice these questions to gain proficiency. Overall, these solutions serve as a valuable resource to enhance your understanding and problem-solving skills in this topic.

Other Related Links for CBSE Class 10 Maths Chapter 3

Chapter-Specific NCERT Solutions for Class 10 Maths

Given below are the chapter-wise NCERT Solutions for Class 10 Maths. Go through these chapter-wise solutions to be thoroughly familiar with the concepts.

NCERT Study Resources for Class 10 Maths

For complete preparation of Maths for CBSE Class 10 board exams, check out the following links for different study materials available at Vedantu.