How To Use Circles Class 9 NCERT PDF For Step By Step Chapter 9 Question Answers And Exam Readiness
NCERT Solutions For Class 9 Maths Chapter 9 Circles (2025-26)
FAQs on NCERT Solutions For Class 9 Maths Chapter 9 Circles (2025-26)
1. How do Vedantu's NCERT Solutions for Class 9 Maths Chapter 9 help in preparing for exams?
Vedantu's NCERT Solutions for Class 9 Maths Chapter 9 are designed by subject experts to provide clear, step-by-step guidance for every problem in the textbook. They help students understand the correct methodology for solving geometric proofs and problems, ensuring answers align with the CBSE 2025-26 marking scheme. This builds a strong conceptual foundation and boosts confidence for exams.
2. What is the best approach to solving problems from NCERT Class 9 Maths Chapter 9 using these solutions?
The most effective approach is to first attempt the problem on your own. Then, use the NCERT solutions to verify your method and answer. Pay close attention to:
- The specific theorem being used.
- The logical flow from 'Given' to 'To Prove'.
- The precise geometric reasons provided for each step.
This method helps in identifying gaps in your understanding rather than simply memorising the solution.
3. Are the problems in NCERT Class 9 Maths Chapter 9, Circles, considered difficult?
For many students, Chapter 9 can be challenging because it heavily relies on understanding and applying geometric theorems. The primary difficulty often lies in visualising the problem and identifying which theorem to apply. The NCERT Solutions help by breaking down complex problems into simpler, manageable steps, making the logical connections easier to follow.
4. What are the key steps to prove that the perpendicular from the centre of a circle bisects the chord?
To solve this common NCERT problem, follow these steps:
- Step 1: Draw the circle with a chord and a perpendicular line from the centre to the chord.
- Step 2: Join the endpoints of the chord to the centre, forming two triangles.
- Step 3: Prove that these two triangles are congruent using the RHS (Right Angle-Hypotenuse-Side) congruence rule. The radii form the hypotenuse, and the perpendicular is the common side.
- Step 4: Conclude that the parts of the chord are equal by CPCTC (Corresponding Parts of Congruent Triangles), thus proving the chord is bisected.
5. How do you correctly apply the theorem that 'equal chords of a circle are equidistant from the centre' in NCERT problems?
When an NCERT problem states that two chords in a circle are equal, you can directly apply this theorem. The key is to correctly identify the 'distance', which is the length of the perpendicular line segment from the centre to the chord. By stating this theorem, you can equate these perpendicular distances to solve for unknown values or prove further properties in the given figure.
6. Why is it essential to provide step-by-step reasoning when solving circle theorems in an exam?
In geometry, the final answer is only part of the solution. According to the CBSE evaluation guidelines, marks are awarded for the logical process and correct reasoning. Each step in a proof must be justified with a known property or theorem. Providing clear, sequential steps demonstrates your conceptual understanding and is crucial for scoring full marks.
7. What is a cyclic quadrilateral, and what is its most important property for solving NCERT questions?
A cyclic quadrilateral is a four-sided figure whose all four vertices lie on the circumference of a single circle. Its most critical property, frequently used in NCERT solutions, is that the sum of its opposite angles is always 180 degrees (i.e., they are supplementary). This property is the key to finding unknown angles in many geometric problems in Chapter 9.
8. How does understanding the relationship between a chord's length and its distance from the centre help in solving complex NCERT problems?
This relationship is fundamental for comparison-based problems. The key concept is: longer chords are closer to the centre and vice-versa. So, if a problem requires you to compare two chords, you can do so by comparing their perpendicular distances from the centre. This allows you to solve problems where the actual lengths of the chords are not given.
9. When solving a problem, how can you distinguish between a chord and the diameter?
A chord is any line segment that connects two distinct points on a circle's circumference. The diameter is a special type of chord that has a unique property: it must pass through the centre of the circle. It is also the longest possible chord in a circle.
10. Can a unique circle be drawn through any three given points? Explain the condition as per the NCERT syllabus.
No, not always. A unique circle can be drawn through three points only if they are non-collinear (meaning they do not all lie on the same straight line). If the three points are collinear, it is impossible to draw a circle that passes through all of them. This is a fundamental theorem explained in Chapter 9.
11. How do concepts like sectors and segments appear in the problems of NCERT Class 9 Maths Chapter 9?
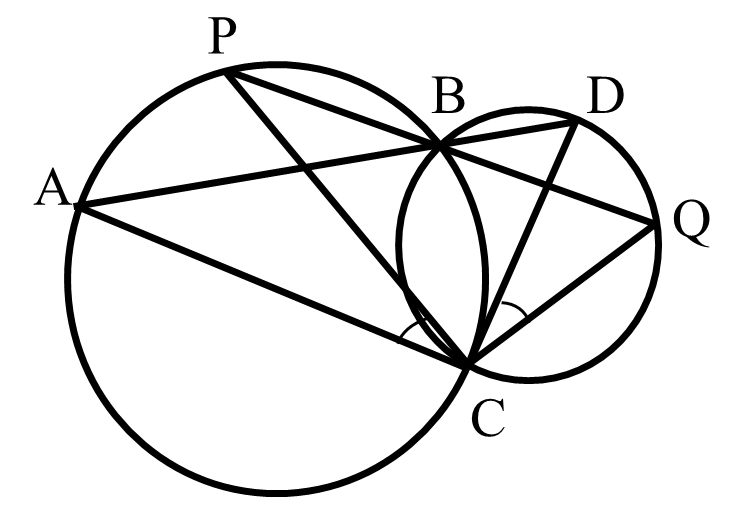
While area calculations for sectors and segments are covered in Class 10, Chapter 9 introduces their definitions. A sector is the region between two radii and an arc, while a segment is the region between a chord and an arc. Understanding these terms is crucial for correctly interpreting problems involving arcs and chords, such as the 'angle in the same segment' theorem.




















 Watch Video
Watch Video