Find Complete Statistics Class 9 Questions And Answers With Detailed Solutions
NCERT Solutions For Class 9 Maths Chapter 12 Statistics (2025-26)
FAQs on NCERT Solutions For Class 9 Maths Chapter 12 Statistics (2025-26)
1. Is a histogram the same as a bar graph in statistics?
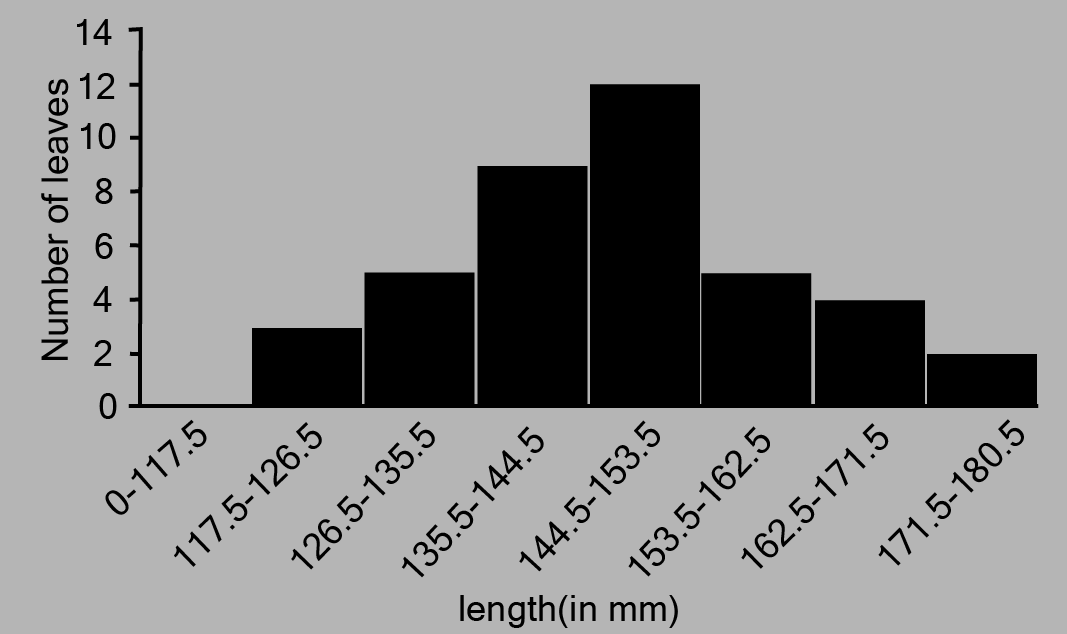
No, a histogram is not the same as a bar graph, although both use rectangular bars to display data. The key difference lies in the type of data they represent and the presence of gaps between the bars.
2. Is the range a measure of central tendency like the mean?
No, the range is a measure of spread or dispersion, not central tendency. It tells you how spread out the data is by showing the difference between the highest and lowest values, unlike the mean, which identifies the central point of the data.
3. Do I have to pay to get the statistics class 9 questions and answers PDF?
No, you do not have to pay for the solutions. Reputable educational platforms like Vedantu provide a Free PDF download of the statistics class 9 ncert solutions, making them accessible for all students to use for practice and revision without any cost.
4. Do NCERT Solutions for Class 9 Maths Chapter 12 only provide the final answers?
NCERT Solutions provide complete, step-by-step explanations for every problem, not just the final answer. Many students mistakenly think these are just answer keys, but they are designed as learning tools that guide you through the entire problem-solving process from start to finish.
5. Can a dataset have more than one mode?
Yes, a dataset can absolutely have more than one mode. If two or more values appear with the same highest frequency, the dataset is called bimodal (two modes) or multimodal (more than two modes). A dataset can also have no mode if all values appear only once.
6. Are the class 9 Maths chapter 12 NCERT solutions only useful for checking homework?
No, the class 9 maths chapter 12 NCERT solutions are valuable tools for complete exam preparation, not just for checking homework. The common myth is that their only purpose is to verify answers after you've finished an assignment.
In reality, these solutions are structured to build conceptual clarity. They explain the correct application of formulas for mean and mode and demonstrate the proper method for drawing histograms and frequency polygons, which are common formats in exams.
7. Is primary data always better to use than secondary data?
No, primary data is not always better than secondary data; the best choice depends on the specific investigation's needs. Students often assume that firsthand data (primary) is more reliable, but collecting it can be expensive, time-consuming, and sometimes impossible.
8. Does the NCERT Statistics Class 9 PDF only contain solutions for the main exercise?
No, a good Statistics Class 9 PDF with solutions typically covers more than just the final exercise problems. The misconception is that it's only a key for end-of-chapter questions like the Ex 12.1 Class 9 Statistics solutions.
In fact, detailed solution PDFs also include explanations for the in-text questions and the solved examples presented within the chapter. This ensures you understand concepts as they are introduced, before you attempt the main exercises.
9. Is it enough to just memorize the steps from the NCERT solution class 9 maths chapter 12?
No, simply memorizing steps is not an effective learning strategy. The purpose of the ncert solution class 9 maths chapter 12 is to help you understand the logic behind each step, so you can apply the same concepts to solve different, unseen problems.
10. Is the class mark just the average of any two numbers in a class interval?
No, the class mark is specifically the average of the upper and lower class limits of a single interval. It is not the average of any random numbers. The formula is fixed: Class Mark = (Upper Class Limit + Lower Class Limit) / 2. It represents the precise midpoint of that class.




















 Watch Video
Watch Video