NCERT Solutions For Class 9 Maths Chapter 6 Lines And Angles in Hindi - 2025-26
NCERT Solutions For Class 9 Maths in Hindi Chapter 6 Lines And Angles (2025-26)
FAQs on NCERT Solutions For Class 9 Maths in Hindi Chapter 6 Lines And Angles (2025-26)
1. Where can I find accurate and step-by-step NCERT Solutions for Class 9 Maths Chapter 6 (Lines and Angles)?
You can find comprehensive and reliable NCERT Solutions for Class 9 Maths Chapter 6 on Vedantu. Our solutions are prepared by subject matter experts and provide a detailed, step-by-step methodology for every problem in the textbook. They are fully aligned with the latest CBSE 2025-26 syllabus, ensuring you learn the correct methods to score well in exams.
2. What are the key concepts I must know to solve problems from Exercise 6.1 in the NCERT textbook?
To master Exercise 6.1, you must have a clear understanding of two fundamental concepts:
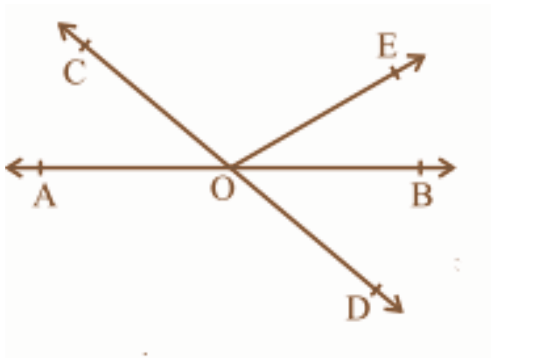
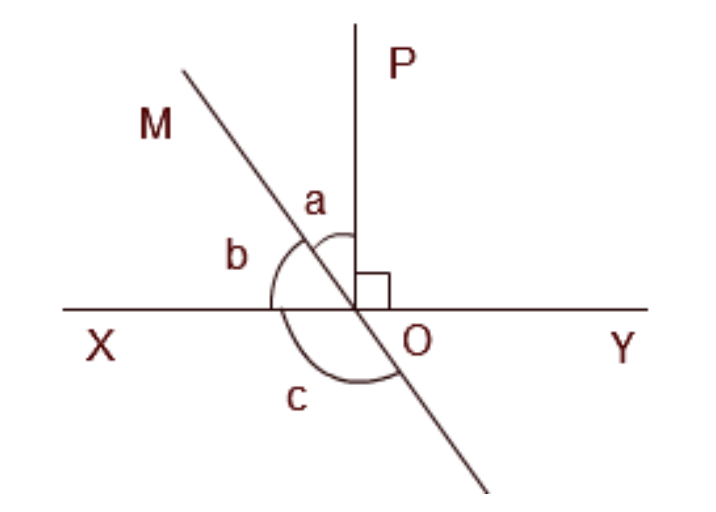
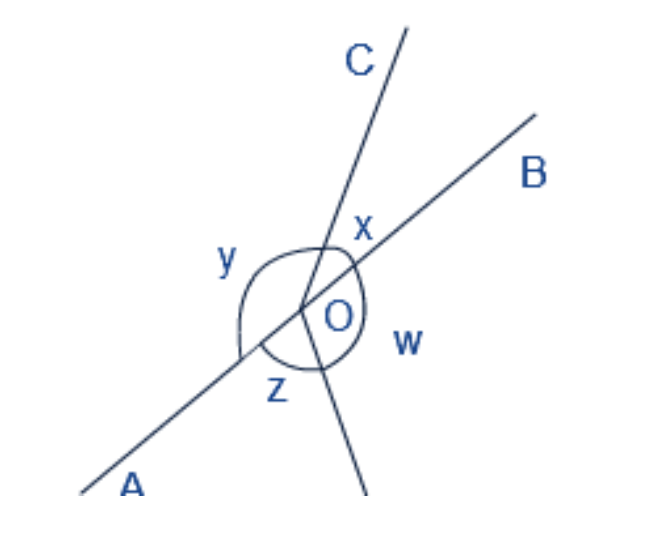
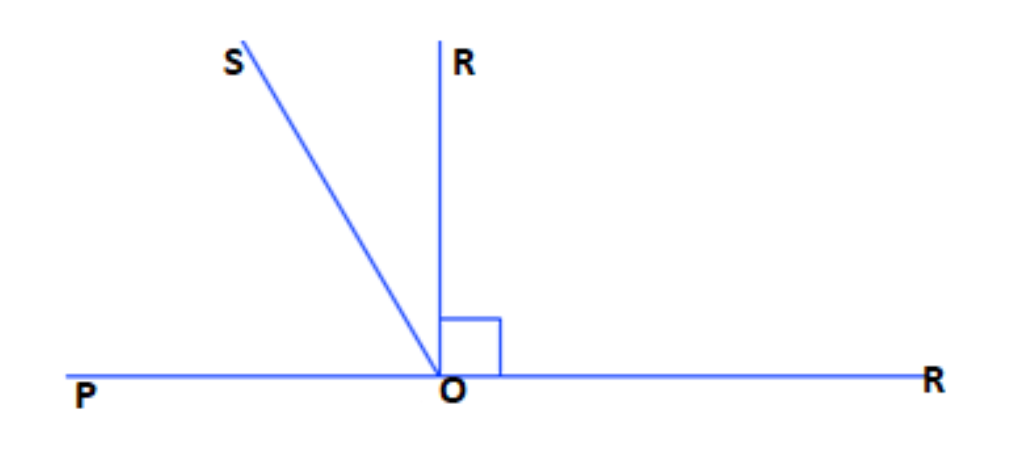
- Linear Pair Axiom: This states that if a ray stands on a line, the sum of the two adjacent angles so formed is 180°.
- Vertically Opposite Angles: When two lines intersect, the angles opposite each other are equal.
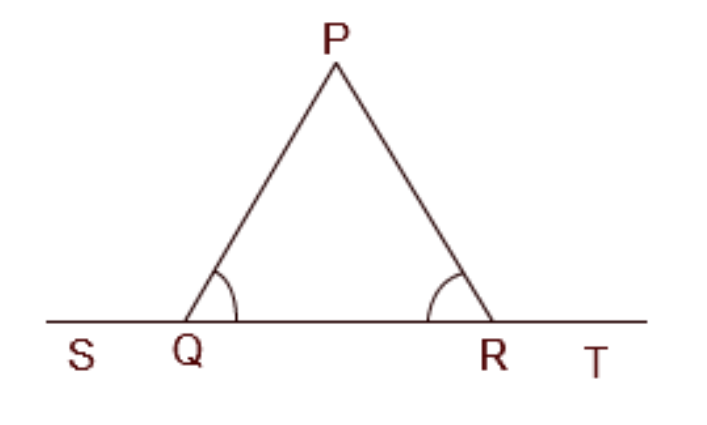
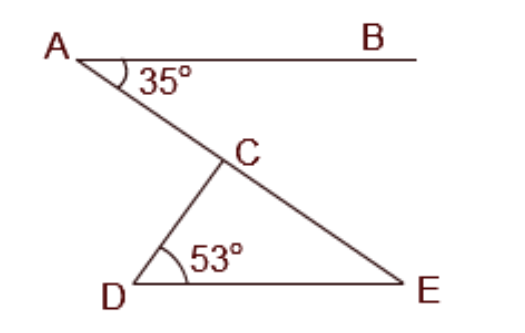
3. How do you correctly apply the Angle Sum Property of a Triangle in Chapter 6 problems?
The Angle Sum Property of a Triangle states that the sum of the interior angles of any triangle is always 180°. To apply this correctly in NCERT solutions, follow these steps:
1. Identify the three interior angles of the triangle in your problem.
2. Write the equation: ∠A + ∠B + ∠C = 180°.
3. Substitute the known values of the angles into the equation.
4. Solve the equation to find the measure of the unknown angle. This property is crucial for many proofs and numerical problems in the chapter.
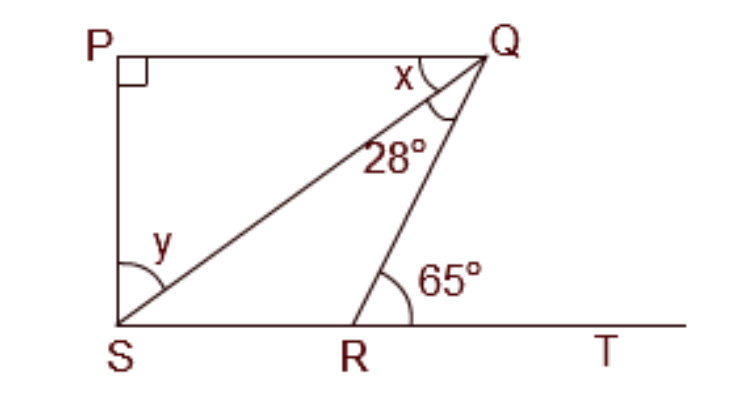
4. What is the most common mistake students make when solving problems with parallel lines and a transversal?
A very common mistake is confusing the relationships between different angle pairs. Students often mix up when angles are equal versus when they are supplementary (add up to 180°). For example, they might incorrectly set consecutive interior angles as equal, when they are actually supplementary. A good way to avoid this is to remember:
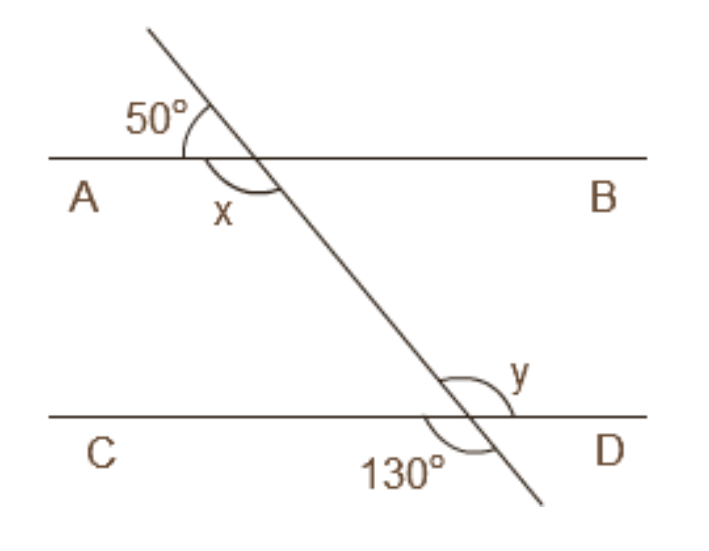
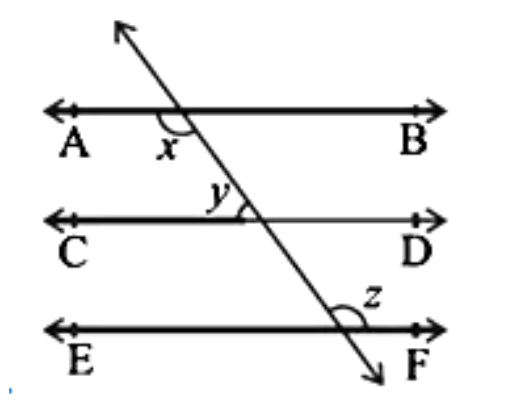
- Alternate Interior Angles are equal.
- Corresponding Angles are equal.
- Consecutive Interior Angles (or co-interior angles) are supplementary.
5. Why is the Linear Pair Axiom referred to as an 'axiom' and not a 'theorem'?
In geometry, an axiom is a fundamental statement that is accepted as true without needing a proof. It's a self-evident truth that forms the basis for proving other statements. The Linear Pair Axiom is considered an axiom because the fact that two adjacent angles on a straight line sum to 180° is a foundational assumption. A theorem, on the other hand, is a statement that is proven to be true using axioms, definitions, and previously proven theorems. For example, the theorem that 'vertically opposite angles are equal' is proven using the Linear Pair Axiom.
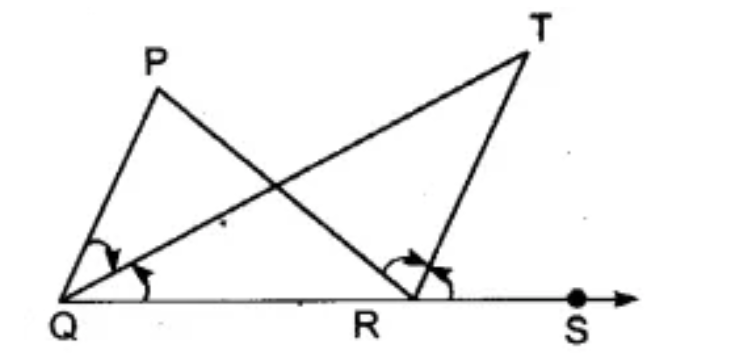
6. What is the correct step-by-step method to prove that two lines are parallel?
To prove that two lines are parallel, you must use the converse of the parallel line theorems. The correct method is:
1. Identify a transversal intersecting the two lines.
2. Use the given information to show that one of the following conditions is true:
- A pair of corresponding angles is equal.
- A pair of alternate interior angles is equal.
- A pair of consecutive interior angles is supplementary (sums to 180°).
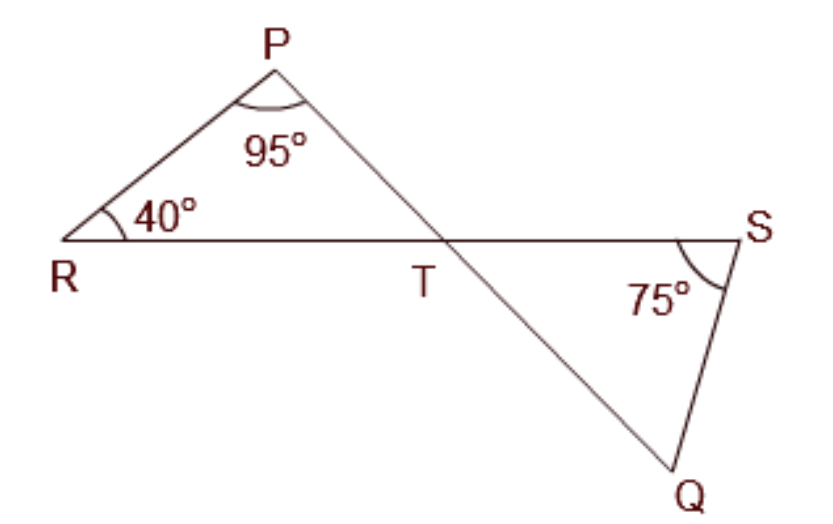
7. How does the Exterior Angle Theorem of a triangle relate to its Angle Sum Property?
The Exterior Angle Theorem is a direct consequence of the Angle Sum Property. The theorem states that an exterior angle of a triangle is equal to the sum of its two opposite interior angles. This can be understood easily:
1. The sum of all three interior angles is 180° (Angle Sum Property).
2. The exterior angle and its adjacent interior angle form a linear pair, so their sum is also 180°.
By comparing these two facts, we can deduce that the exterior angle must be equal to the sum of the other two interior angles. This shows how geometric theorems are logically interconnected.
8. What is the difference in solving a problem that asks for an angle versus one that asks for a reflex angle?
The method of solving differs in the final step. An 'angle' typically refers to the measurement between 0° and 180°. A reflex angle is the larger angle that measures more than 180° but less than 360°. To find a reflex angle for a known angle 'x', you must subtract the angle from 360°. The correct formula is:
Reflex Angle = 360° - x.
Always check the question carefully to see if it specifies 'reflex angle' to avoid losing marks.
9. How important is it to solve the NCERT textbook examples for Chapter 6 before starting the exercises?
It is extremely important. The solved examples in the NCERT textbook are not just practice problems; they are designed to demonstrate the correct application of theorems and axioms. They often introduce specific problem-solving patterns and the formal way to write proofs, which are essential for the exercises and for exams. Following the method shown in these examples ensures you are aligned with the CBSE curriculum's expectations.




















 Watch Video
Watch Video