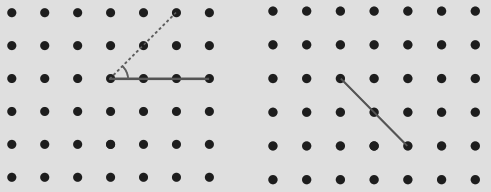
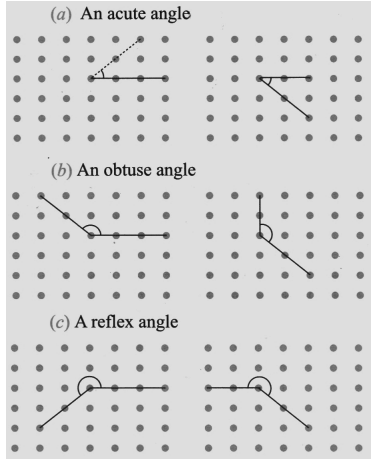
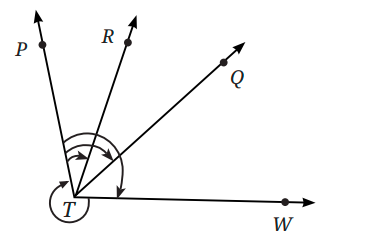
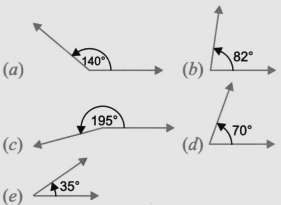
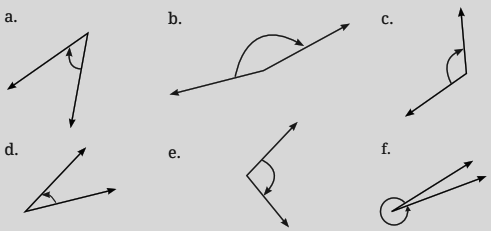
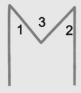
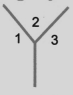
Lines And Angles Class 6 Questions and Answers - Free PDF Download
NCERT Solutions for Class 6 Maths Chapter 2, Exercise 2.11, "Lines and Angles," helps students practise measuring and classifying different types of angles. This exercise focuses on using a protractor to accurately measure angles, an important skill for understanding geometric concepts. It follows the CBSE Class 6 Maths Syllabus and provides clear, step-by-step instructions to help students measure angles correctly.
Table of Content
Students can download these NCERT Solutions as a FREE PDF for easy practice and better understanding. NCERT Solutions for Class 6 include practical tips and simple methods, making the learning process engaging and easy to follow. By using these solutions, students can improve their angle measurement skills, which will prepare them for more advanced geometry topics in future lessons.
Glance on NCERT Solutions Maths Chapter 2 Exercise 2.11 Class 6 | Vedantu
This exercise helps students learn about different types of angles such as acute, obtuse, right, and straight angles.
Students practise using a protractor to measure angles accurately, understanding how to find the degree measure of each angle.
The exercise teaches students to classify angles based on their measures, like angles less than 90° (acute) and angles greater than 90° but less than 180° (obtuse).
The solutions provide easy-to-follow instructions for measuring and classifying each type of angle.
Examples are included to help students see how these angle concepts apply to real-life situations.
Students get the opportunity to reinforce their understanding through various practice problems on angle measurement and classification.
Exercise 2.11
1. In each of the below grids, join A to other grid points in the figure by a straight line to get:
a. An acute angle
b. An obtuse angle
c. A reflex angle
Mark the intended angles with curves to specify the angles. One has been done for you.
Ans:
2. Use a protractor to find the measure of each angle. Then classify each angle as acute, obtuse, right, or reflex.
a. ∠PTR b. ∠PTQ c. ∠PTW d. ∠WTP
Ans: (a) ∠PTR = 300° is a reflex angle, as it is greater than 180°.
(b) ∠PTQ = 60° is an acute angle because it is less than 90°.
(c) ∠PTW = 105° is an obtuse angle, as it is greater than 90° but less than 180°.
(d) ∠WTP = 225° is a reflex angle, as it exceeds 180°.
Each of these angles has been categorized based on its measurement, showing the differences between acute, obtuse, and reflex angles. These types of angles are important for understanding basic geometry and for practical applications in various real-world contexts.
3. Draw angles with the following degree measures:
a. 140° b. 82° c. 195° d. 70° e. 35°
Ans:
4. Estimate the size of each angle and then measure it with a protractor:
Classify these angles as acute, right, obtuse or reflex angles
Ans: (a) A 45° angle is classified as acute, as it is less than 90°.
(b) A 150° angle is considered obtuse since it is greater than 90° but less than 180°.
(c) A 120° angle is also an obtuse angle, falling between 90° and 180°.
(d) A 30° angle is an acute angle, being smaller than 90°.
(e) A 95° angle is classified as obtuse, as it is slightly greater than 90°.
(f) A 350° angle is a reflex angle, as it is greater than 180° but less than 360°.
Each of these angles demonstrates the different types—acute, obtuse, and reflex—based on their measures. Understanding how to classify angles is an important skill in geometry, helping in tasks like designing, constructing, and analysing shapes in real-life contexts.
5. Make any figure with three acute angles, one right angle and two obtuse angles.
Ans:
Angles 1, 2, and 3 are classified as acute angles, as each is less than 90°. Angle 4 is a right angle, meaning it measures exactly 90°. Angles 5 and 6 are obtuse, as they are greater than 90° but less than 180°.
These angles cover the basic types commonly seen in geometry—acute, right, and obtuse. Knowing how to identify and classify these angles is essential for understanding geometric shapes and solving problems related to construction, design, and real-world applications of angles.
6. Draw the letter ‘M’ such that the angles on the sides are 40° each and the angle in the middle is 60°.
Ans:
Angle ∠1 measures 30°, angle ∠2 is also 30°, and angle ∠3 measures 60°. Both ∠1 and ∠2 are acute angles, as they are less than 90°, while ∠3 is slightly larger but still acute, as it is less than 90° as well.
These angles are typical in many geometric shapes, such as triangles. Understanding these different measurements is important for analyzing shapes, solving problems involving angles, and applying these concepts to practical tasks like architecture or engineering.
7. Draw the letter ‘Y’ such that the three angles formed are 150°, 60° and 150°.
Ans:
Angle ∠1 measures 150°, angle ∠2 is 60°, and angle ∠3 is also 150°. Both ∠1 and ∠3 are obtuse angles, as they are greater than 90° but less than 180°, while ∠2 is an acute angle, as it is smaller than 90°.
These angle measures often appear in geometric shapes such as irregular polygons. Understanding the differences between acute and obtuse angles is key for solving geometry problems and applying this knowledge in real-life contexts, such as construction or design.
8. The Ashoka Chakra has 24 spokes. What is the degree measure of the angle between two spokes next to each other? What is the largest acute angle formed between two spokes?
Ans: The angle between two consecutive spokes is calculated as 360° ÷ 24, which equals 15°. The largest acute angle can be found by multiplying 15° by 5, resulting in 75°.
These calculations are useful when analysing symmetrical objects like wheels or gears, where equal spacing is important. Understanding how to divide a circle into equal angles helps in various practical applications, from designing mechanical parts to creating artistic patterns. The largest acute angle in this example, 75°, is commonly seen in many geometric constructions.
9. Puzzle: I am an acute angle. If you double my measure, you get an acute angle. If you triple my measure, you will get an acute angle again. If you quadruple (four times) my measure, you will get an acute angle yet again! But if you multiply my measure by 5, you will get an obtuse angle measure. What are the possibilities for my measure?
Ans: Let the measure of the angle be denoted as m. According to the conditions, 5 × m is greater than 90°, but 4 × m is less than 90°. This gives the inequality $\frac{90}{5}$ < m < $\frac{90}{4}$.
Thus, m must be greater than 18° but less than 22½°. Based on this, the possible measures for the angle are 19°, 20°, or 21°.
This method of solving inequalities helps in determining specific angle ranges, which is useful in geometric problems that require finding suitable angle measures within a set of conditions. Understanding this approach can be applied in various situations, such as designing objects with specific angular constraints.
Benefits of NCERT Solutions for Class 6 Chapter 2 Lines and Angles Exercise 2.11
The solutions provide clear and simple instructions to help students measure and classify different types of angles, making the learning process easier.
By using a protractor, students gain hands-on experience in measuring angles accurately, which is important for geometry.
The solutions help students understand the differences between acute, obtuse, right, and straight angles, improving their ability to classify angles.
Real-life examples are included, helping students relate angle concepts to everyday situations and making the topic more engaging.
The practice problems offer students the chance to apply what they have learned, reinforcing their skills in measuring and classifying angles.
Class 6 Maths Chapter 2: Exercises Breakdown
Important Study Material Links for Class 6 Maths Chapter 2 - Lines and Angles
Conclusion
NCERT Solutions for Class 6 Maths Chapter 2, Exercise 2.11, "Lines and Angles," helps students understand the different types of angles and how to measure them accurately. The clear explanations make it easier to classify angles, such as acute, obtuse, and right angles. Practising these exercises improves student’s skills in measuring and identifying angles, which is important for understanding geometry. With the solutions available as a FREE PDF download, students can study and review at their own pace, making learning both simple and effective.
Chapter-wise NCERT Solutions Class 6 Maths
The chapter-wise NCERT Solutions for Class 6 Maths are given below. Go through these chapter-wise solutions to be thoroughly familiar with the concepts.
Related Important Links for Class 6 Maths
Along with this, students can also download additional study materials provided by Vedantu for Maths Class 6.
FAQs on NCERT Solutions For Class 6 Maths Chapter 2 Lines And Angles Exercise 2.11 - 2025-26
1. Where can I find reliable, step-by-step NCERT Solutions for Class 6 Maths Chapter 2 (Whole Numbers)?
You can find comprehensive and reliable NCERT Solutions for Class 6 Maths Chapter 2, Whole Numbers, right here on Vedantu. Our solutions are crafted by subject matter experts to provide a clear, step-by-step methodology for solving every problem in the textbook, ensuring they align perfectly with the latest CBSE 2025-26 guidelines.
2. How do the NCERT Solutions for Chapter 2 explain the method to find the predecessor and successor of a given whole number?
The NCERT Solutions provide a very straightforward method for this. To find the successor of a whole number, you simply add 1 to it. For example, the successor of 99 is 99 + 1 = 100. To find the predecessor, you subtract 1 from the number. For example, the predecessor of 100 is 100 - 1 = 99. The solutions clarify that the whole number 0 does not have a predecessor in whole numbers.
3. What is the correct process to solve problems using the distributive property as shown in the Chapter 2 solutions?
The solutions explain the distributive property of multiplication over addition with clear steps to simplify calculations. The method involves breaking down one of the numbers into a sum. For example, to calculate 24 x 105, you would:
Rewrite 105 as (100 + 5).
Apply the property: 24 x (100 + 5).
Distribute the multiplication: (24 x 100) + (24 x 5).
Solve the simpler products: 2400 + 120.
Add the results to get the final answer: 2520.
4. How do the solutions demonstrate the representation of whole number operations on a number line?
The NCERT solutions clearly illustrate how to use a number line for operations. For addition (e.g., 3 + 4), you start at 3 and make 4 jumps to the right, landing on 7. For subtraction (e.g., 7 - 5), you start at 7 and make 5 jumps to the left, landing on 2. This visual method helps in understanding how numbers are ordered and manipulated.
5. Are the NCERT Solutions for Class 6 Maths Chapter 2 provided by Vedantu updated for the 2025-26 academic year?
Yes, all our NCERT Solutions, including those for Class 6 Maths Chapter 2, are meticulously updated to align with the official CBSE/NCERT syllabus for the 2025-26 academic session. You can rely on them for accurate and current methods for your homework and exam preparation.
6. Why is division of a whole number by zero considered 'not defined' in the NCERT syllabus?
The NCERT syllabus explains that division by zero is undefined because it leads to a mathematical contradiction. Division is the inverse of multiplication. For example, 8 ÷ 2 = 4 because 4 x 2 = 8. If we try to calculate 8 ÷ 0, we would be looking for a number that, when multiplied by 0, gives 8. However, any number multiplied by 0 is 0, not 8. Since no such number exists, the operation is not defined.
7. What is the significance of '0' (zero) and '1' (one) as identity elements for whole numbers?
The NCERT solutions explain their significance as follows:
Zero (0) is the additive identity: Adding 0 to any whole number does not change its value (e.g., 5 + 0 = 5). This property is fundamental in algebra for solving equations.
One (1) is the multiplicative identity: Multiplying any whole number by 1 does not change its value (e.g., 5 x 1 = 5). This is a key principle used in simplifying fractions and algebraic expressions.
8. Why don't the closure and commutative properties apply to the subtraction of whole numbers?
The solutions explain this with clear examples. Closure property means performing an operation on two whole numbers results in a whole number. Subtraction is not closed because 3 - 5 = -2, and -2 is not a whole number. Commutative property means the order of numbers does not affect the result. Subtraction is not commutative because 5 - 3 = 2, but 3 - 5 = -2. Since 2 is not equal to -2, the order matters, and the property does not hold.
