Maths Notes for Chapter 13 Symmetry Class 6 - FREE PDF Download
Definition of Symmetry
An object when cut or folded into two halves about a line or axis such that the proportions of both halves are completely balanced is called symmetry. In a simpler way, the two halves should be mirror images to each other and when one half is placed over another one gets completely superimposed. For example, the two halves of a human face, or a butterfly, an earthen pot, a glass etc. as shown in the image below;
Line or Axis of Symmetry
The line or axis through which the object is folded or divided is called the line or axis of symmetry. Generally, all the regular shapes are symmetrical about at least one axis and many irregular shapes can also be defined as symmetrical upon the proper selection of the axis.
One figure can have one or more lines of symmetry. The examples of shapes with their number of lines of symmetries have been tabulated below;
The diagrams can be illustrated as below;
Similarly, a circular object or shape can also have the infinite number of lines of symmetry.
Types of the Line of Symmetry
Vertical Line of Symmetry – When an object or shape is divided into two identical halves by a straight standing or vertical line, then it is called a vertical line of symmetry as shown in the diagram below.
Horizontal Line of Symmetry – When an object or shape is divided into two identical halves by a sleeping straight or horizontal line, then it is called a horizontal line of symmetry as shown in the diagram below.
Diagonal Line of Symmetry – When an object or shape is divided into two identical halves by a diagonal line, then it is called a diagonal line of symmetry as shown in the diagram below.
Reflection and Symmetry
As stated earlier, one half of an object about its line of symmetry forms a mirror image of the other half. This is similar to the case of an actual plane mirror and the phenomenon associated with it. Reflection is the phenomenon through which mirror images are formed and it can be noticed that if an object it placed in front of a mirror, the reflection inside the mirror is purely identical such that all the lengths and angles are the same.
Although there is just one difference that can be found in reflection symmetry which we notice when we stand in front of a mirror is that the orientation changes and the left-right get reversed.
Application of Symmetry in Day-To-Day Life
Symmetry has a very wide range of applications and uses and is directly or indirectly present in every aspect of our life. Ranging from just a small nut to famous architectural beauties and monuments, symmetry is present. A very common example known is rangoli or the geometrical designs. Many parts or equipment of a machine are symmetrical in nature.
Class 6 Maths Notes of Symmetry
Class 6 Maths Chapter 13 revision notes provided by Vedantu aims to help students revise each and every important concept related to symmetry in detail. It is beneficial to understand the important concepts related to symmetry that have been taught in class as these concepts are the stepping stones for the upcoming senior classes. To revise your symmetry concepts thoroughly, it is important to study the Maths Class 6 Symmetry Notes.
Class 6 Maths Chapter 13 revision notes are prepared by the subject experts at Vedantu. The subject experts at Vedantu have formulated symmetry Class 6 notes as per the latest CBSE syllabus and academic subject material. By studying Class 6 Maths Chapter 13 revision notes, you will not find any difficulty to solve the questions based on symmetry in the exam.
With the help of the Class 6 Maths notes of Symmetry, you can revise the chapter symmetry in a concise manner. Maths Class 6 Symmetry notes are the excellent study material offered by Vedantu as these are prepared by the experienced teachers. The notes are written in an easy language that helps you to revise the entire chapter within no time. After studying these notes of symmetry offered by Vedantu, you will be in a position to solve every question related to a chapter within no time. So, it is advised to study the symmetry Class 6 notes without any confusion. You can easily download Class 6 revision notes symmetry by clicking on the PDF link given below.
Download Class 6 Revision Notes Symmetry - Free PDF
Vedantu offers the best and most reliable Class 6 revision notes of symmetry that includes all important concepts and topics of the chapter. Class 6 students are advised to study these revision notes thoroughly as these notes will not merely help them to crack Class 6 exams but also help them to prepare for other competitive exams. You can easily download Class 6 revision notes symmetry just with one single click on the PDF link given below. It is available free of cost by Vedantu and you can refer to symmetry Class 6 notes both online and offline.
These revision notes are one of the most important pieces of study material that CBSE Class 6 students can use as It will make their learning simple and convenient These are reliable notes as it is prepared by the excellent teachers at Vedantu after the extensive research of the topic. You can download Class 6 Maths Chapter 13 revision notes in PDF format and use them to revise all the concepts that are learned before and hence score better marks in their final exam.
About Symmetry
In Mathematics, the meaning of Symmetry states that one shape is exactly similar to the other shape when it is flipped, turned, or rotated. Symmetry is an important concept in geometry and the symmetry objects can be found all around us in nature, architecture, and art.
The definition of the symmetry states that symmetry is a balanced and proportion similarity that is found in two halves of the object i.e. one half of the object is the mirror image of the other half of the object. The imaginary line which is used to fold a figure to get the symmetrical halves is known as the line of symmetry.
Line of Symmetry
An imaginary line or axis along which the figure can be folded to get the symmetrical halves is known as the line of symmetry. Generally, it divides an object into two mirror-image halves. The line of symmetry can either be horizontal, vertical, or diagonal.
Types of Symmetry
Reflective Symmetry - Reflection is a type of symmetry that is related to reflections. It is also known as line symmetry or mirror symmetry. The definition of reflective symmetry states that there exists a minimum one line that divides the figure into two halves such that one half of the object is the mirror image of the other half of the object.
Rotational Symmetry - The rotational symmetry states that whenever an object is rotated on its axis, the shape of the object looks the same. Many geometrical figures such as square, circle, regular hexagon, etc have rotational symmetry.
Benefits of Class 6 Maths Chapter 13 Revision Notes
Some of the benefits of Class 6 Maths Chapter 13 revision notes are discussed below:
Enable the students to strengthen their symmetry concepts.
Student’s become more confident during examinations.
Student's anxiety level and exam stress get minimized.
Minimize the chance of making silly mistakes.
Help to save valuable time during the examination.
The accuracy of concepts explained in the Class 6 revision notes symmetry is high.
Class 6 Maths Chapter 13 Revision Notes PDF are available free of cost and can be accessed by the students both online and offline.
Conclusion
The Symmetry Class 6 Notes for CBSE Maths Chapter 13 provide an excellent resource for students exploring the fascinating world of symmetry in mathematics. The free PDF download offers a comprehensive overview of key concepts, accompanied by illustrative examples and exercises. These notes serve as a valuable aid in enhancing students' understanding of symmetry, guiding them through practical applications and problem-solving. Whether used for revision or as a primary learning tool, these notes contribute to a solid foundation in mathematics for Class 6 students, making the exploration of symmetry an engaging and rewarding experience.
FAQs on Symmetry Class 6 Maths Chapter 13 CBSE Notes - 2025-26
1. What are the key concepts to focus on when revising Symmetry for Class 6?
For a quick and effective revision of Class 6 Maths Chapter 13, Symmetry, you should focus on the following core concepts:
The basic definition of symmetry and what makes a figure symmetrical.
Identifying the line of symmetry (or axis of symmetry) in various geometric shapes.
Understanding the difference between figures with one, two, or multiple lines of symmetry.
The relationship between reflection and symmetry, using a mirror line as a practical example.
Recognising symmetrical patterns in everyday objects and the English alphabet.
2. How can you quickly define a line of symmetry in a figure?
A line of symmetry is an imaginary line that divides a figure into two identical halves. If you were to fold the figure along this line, one half would perfectly overlap the other half. For a quick check, you can visualise placing a mirror on the line; the reflection of one half should perfectly match the other half.
3. How does the concept of reflection relate to symmetry?
Reflection and symmetry are closely related concepts. The line of symmetry acts exactly like a mirror line. The part of the figure on one side of the line is the perfect reflection of the part on the other side. This means every point on one half of the figure is at the same perpendicular distance from the line of symmetry as its corresponding point on the other half.
4. Can a figure have more than one line of symmetry? Explain with an example.
Yes, a figure can have multiple lines of symmetry. For a quick recap, consider these examples:
A rectangle has two lines of symmetry: one horizontal and one vertical, passing through its centre.
A square has four lines of symmetry: two that pass through the midpoints of opposite sides and two that are its diagonals.
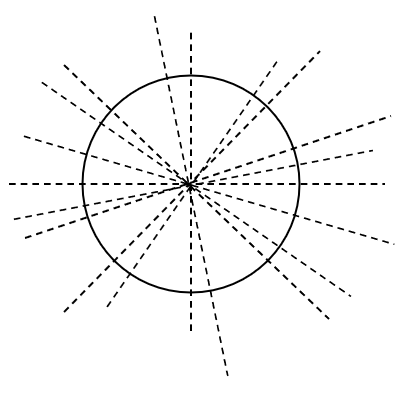
A circle has infinite lines of symmetry, as any line passing through its centre will divide it into two identical semicircles.
5. What is the difference between symmetrical and asymmetrical figures?
The key difference lies in whether a line of symmetry can be drawn. A symmetrical figure is one that can be divided by at least one line of symmetry into two identical halves. Examples include squares, equilateral triangles, and the letter 'A'. An asymmetrical figure is a figure that has no line of symmetry; it cannot be divided into two identical halves by any straight line. Examples include a scalene triangle and the letter 'J'.
6. Which letters of the English alphabet have a vertical line of symmetry?
For a quick revision of vertical symmetry, you can recall the following capital letters from the English alphabet: A, H, I, M, O, T, U, V, W, X, and Y. Each of these letters can be divided by a vertical line into two identical, mirror-image halves.
7. What is the best way to revise the chapter on Symmetry to ensure all concepts are covered?
A good revision strategy for Symmetry is to start with the basics and build from there. First, master the definition of symmetry and the line of symmetry. Then, practice identifying these lines in simple shapes. Progress to more complex shapes with multiple lines of symmetry. Finally, connect the concept to real-world examples like architecture, nature, and art to solidify your understanding. Drawing figures and their lines of symmetry is an excellent way to revise.
