NCERT Solutions For Class 9 Maths Chapter 1 Number Systems

• Exercise 1.1: This exercise covers basic concepts of the number system, such as natural numbers, whole numbers, integers, rational numbers, irrational numbers, etc. The questions in this exercise aim to familiarise students with these concepts and their properties.

• Exercise 1.2: This exercise covers the representation of numbers in decimal form. The questions in this exercise require students to convert fractions into decimals, decimals into fractions, and perform basic operations such as addition, subtraction, multiplication, and division on decimals.

• Exercise 1.3: This exercise deals with the representation of rational numbers on a number line. The questions in this exercise require students to mark the position of given rational numbers on a number line and identify the rational number represented by a given point on the number line.

• Exercise 1.4: This exercise deals with the conversion of recurring decimals into fractions. The questions in this exercise require students to write recurring decimals as fractions and vice versa.

• Exercise 1.5: This exercise covers the comparison of rational numbers. The questions in this exercise require students to compare given rational numbers using the concept of inequality, find rational numbers between two given rational numbers, and represent rational numbers on a number line.

NCERT Solutions Class 9 Maths Chapter 1 Number System - Free PDF Download

Exercise (1.1)

1.  Is zero a rational number? Can you write it in the form  $\dfrac{ {p}}{ {q}}$, where $ {p}$ and $ {q}$ are integers and $ {q}\ne  {0}$? Describe it.

Ans: Remember that, according to the definition of rational number,

a rational number is a number that can be expressed in the form of  $\dfrac{p}{q}$, where $p$ and $q$ are integers and  $q\ne \text{0}$.

Now, notice that zero can be represented as $\dfrac{0}{1},\dfrac{0}{2},\dfrac{0}{3},\dfrac{0}{4},\dfrac{0}{5}.....$

Also, it can be expressed as $\dfrac{0}{-1},\dfrac{0}{-2},\dfrac{0}{-3},\dfrac{0}{-4}.....$

Therefore, it is concluded from here that $0$ can be expressed in the form of $\dfrac{p}{q}$, where $p$ and $q$ are integers.

Hence, zero must be a rational number.

2. Find any six rational numbers between $ {3}$ and $ {4}$. 

Ans: It is known that there are infinitely many rational numbers between any two numbers. Since we need to find $6$ rational numbers between $3$ and $4$, so multiply and divide the numbers by $7$ (or by any number greater than $6$)

Then it gives, 

$ 3=3\times \dfrac{7}{7}=\dfrac{21}{7} $ 

$  4=4\times \dfrac{7}{7}=\dfrac{28}{7} $

Hence, $6$ rational numbers found between $3$ and $4$ are $\dfrac{22}{7},\dfrac{23}{7},\dfrac{24}{7},\dfrac{25}{7},\dfrac{26}{7},\dfrac{27}{7}$.

3. Find any five rational numbers between $\dfrac{ {3}}{ {5}}$ and $\dfrac{ {4}}{ {5}}$.

Ans: It is known that there are infinitely many rational numbers between any two numbers.

Since here we need to find five rational numbers between $\dfrac{3}{5}$ and $\dfrac{4}{5}$,  so multiply and divide by $6$ (or by any number greater than $5$).

Then it gives,

$\dfrac{3}{5}=\dfrac{3}{5}\times \dfrac{6}{6}=\dfrac{18}{30}$,

$\dfrac{4}{5}=\dfrac{4}{5}\times \dfrac{6}{6}=\dfrac{24}{30}$.

Hence, $5$ rational numbers found between $\dfrac{3}{5}$ and $\dfrac{4}{5}$ are

$\dfrac{19}{30},\dfrac{20}{30},\dfrac{21}{30},\dfrac{22}{30},\dfrac{23}{30}$.

4. State whether the following statements are true or false. Give reasons for your answers. 

(i) Every natural number is a whole number. 

Ans: Write the whole numbers and natural numbers in a separate manner.

It is known that the whole number series is $0,1,2,3,4,5.....$. and the natural number series is $1,2,3,4,5...$.

Therefore, it is concluded that all the natural numbers lie in the whole number series as represented in the diagram given below.

Thus, it is concluded that every natural number is a whole number.

Hence, the given statement is true.

(ii) Every integer is a whole number.

Ans: Write the integers and whole numbers in a separate manner.

It is known that integers are those rational numbers that can be expressed in the form of $\dfrac{p}{q}$, where $q=1$.

Now, the series of integers is like $0,\,\pm 1,\,\pm 2,\,\pm 3,\,\pm 4,\,...$.

But the whole numbers are $0,1,2,3,4,...$.

Therefore, it is seen that all the whole numbers lie within the integer numbers, but the negative integers are not included in the whole number series.

Thus, it can be concluded from here that every integer is not a whole number.

Hence, the given statement is false.

(iii) Every rational number is a whole number.

Ans: Write the rational numbers and whole numbers in a separate manner.

It is known that rational numbers are the numbers that can be expressed in the form  $\dfrac{p}{q}$, where $q\ne 0$ and the whole numbers are represented as $0,\,1,\,2,\,3,\,4,\,5,...$

Now, notice that every whole number can be expressed in the form of $\dfrac{p}{q}$

as  \[\dfrac{0}{1},\text{ }\dfrac{1}{1},\text{ }\dfrac{2}{1},\text{ }\dfrac{3}{1},\text{ }\dfrac{4}{1},\text{ }\dfrac{5}{1}\],…

Thus, every whole number is a rational number, but all the rational numbers are not whole numbers. For example,

$\dfrac{1}{2},\dfrac{1}{3},\dfrac{1}{4},\dfrac{1}{5},...$ are not whole numbers.

Therefore, it is concluded from here that every rational number is not a whole number.

Hence, the given statement is false.

Exercise (1.2)

1. State whether the following statements are true or false. Justify your answers.

(i) Every irrational number is a real number. 

Ans: Write the irrational numbers and the real numbers in a separate manner.

• The irrational numbers are the numbers that cannot be represented in the form $\dfrac{p}{q},$ where $p$ and $q$ are integers and $q\ne 0.$

For example, $\sqrt{2},3\pi ,\text{ }.011011011...$ are all irrational numbers.

• The real number is the collection of both rational numbers and irrational numbers.

For example, $0,\,\pm \dfrac{1}{2},\,\pm \sqrt{2}\,,\pm \pi ,...$ are all real numbers.

Thus, it is concluded that every irrational number is a real number.

Hence, the given statement is true.

(ii) Every point on the number line is of the form $\sqrt{m}$, where m is a natural number. 

Ans: Consider points on a number line to represent negative as well as positive numbers.

Observe that, positive numbers on the number line can be expressed as $\sqrt{1,}\sqrt{1.1,}\sqrt{1.2},\sqrt{1.3},\,...$, but any negative number on the number line cannot be expressed as $\sqrt{-1},\sqrt{-1.1},\sqrt{-1.2},\sqrt{-1.3},...$, because these are not real numbers.

Therefore, it is concluded from here that every number point on the number line is not of the form $\sqrt{m}$, where $m$ is a natural number.

Hence, the given statement is false.

(iii) Every real number is an irrational number. 

Ans: Write the irrational numbers and the real numbers in a separate manner.

• The irrational numbers are the numbers that cannot be represented in the form $\dfrac{p}{q},$ where $p$ and $q$ are integers and $q\ne 0.$

For example, $\sqrt{2},3\pi ,\text{ }.011011011...$ are all irrational numbers.

• Real numbers are the collection of rational numbers (Ex: $\dfrac{1}{2},\dfrac{2}{3},\dfrac{3}{5},\dfrac{5}{7},$……) and the irrational numbers (Ex: $\sqrt{2},3\pi ,\text{ }.011011011...$).

Therefore, it can be concluded that every irrational number is a real number, but

every real number cannot be an irrational number.

Hence, the given statement is false.

2. Are the square roots of all positive integer numbers irrational? If not, provide an example of the square root of a number that is not an irrational number.

Ans: Square root of every positive integer does not give an integer.

For example: $\sqrt{2},\sqrt{3,}\sqrt{5},\sqrt{6},...$ are not integers, and hence these are irrational numbers. But $\sqrt{4}$ gives $\pm 2$ , these are integers and so, $\sqrt{4}$ is not an irrational number.

Therefore, it is concluded that the square root of every positive integer is not an irrational number.

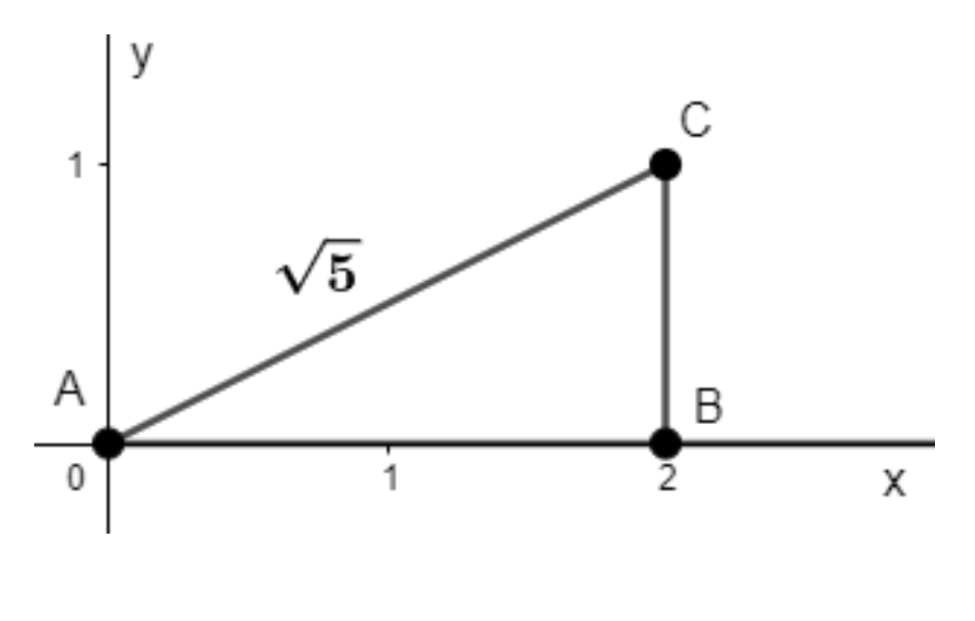
3. Represent $\sqrt{5}$ on the number line.

Ans: Follow the procedures to get $\sqrt{5}$ on the number line.

• Firstly, Draw a line segment $AB$ of $2$ unit on the number line.

• Secondly, draw a perpendicular line segment $BC$ at $B$ of $1$ units.

• Thirdly, join the points $C$ and $A$, to form a line segment $AC$. 

• Fourthly, apply the Pythagoras Theorem as 

$ A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}} $

$  A{{C}^{2}}={{2}^{2}}+{{1}^{2}} $

$ A{{C}^{2}}=4+1=5 $

$ AC=\sqrt{5} $

• Finally, draw the arc $ACD$, to find the number $\sqrt{5}$ on the number line as given in the diagram below.

Exercise (1.3)

1. Write the following in decimal form and say what kind of decimal expansion each has:

(i) $\mathbf{\dfrac{ {36}}{ {100}}}$

Ans: Divide $36$ by $100$. 

$\,\,\,\,\,\,\,\,\,\, {0.36}$

$100 {\overline{)\;36\quad}}$

$\underline{\,\,\,\,\,\,\,\,\,-0\quad}$

$\,\,\,\,\,\,\,\,\,\,\,\,\,\,360$

$\underline{\,\,\,\,\,\,\,\,\,\,-300\quad}$

$\;\;\,\,\,\,\,\,\,\,\,\,\,\,\,\,600$

$\underline{\,\,\,\,\,\,\,\,\,\,\,\,\,-600}$

$\underline{\,\,\,\,\,\,\,\,\,\,\,\,\quad 0 \,\,\,\,\,}$

So, $\dfrac{36}{100}=0.36$ and it is a terminating decimal number.

(ii) $\mathbf{\dfrac{ {1}}{ {11}}}$

Ans: Divide $1$ by $11$.

${\,\,\,\,\,\,\,\,0.0909..}$

$11 \, {\overline{)\;1\quad}}$

$\underline{\,\,\,\,\,\,\,-0\quad}$

$\,\,\,\,\,\,\,\,\,\,10$

$\underline{\,\;\;\,\,-0\quad}$

$\;\;\,\,\,\,100$

$\underline{\,\,\,\,\;-99}$

$\,\,\,\,\,\, \quad 10$

$\quad\underline{\;\;-0\quad}$

$\;\;\,\,\,\,\,\,\,\,100$

$\underline{\,\,\,\,\,\,\,\,\;-99}$

$\quad\,\,\,\,\,\,\,1\quad$

It is noticed that while dividing $1$ by $11$, in the quotient $09$ is repeated.

So, $\dfrac{1}{11}=0.0909.....$ or 

$\dfrac{1}{11}=0.\overline{09}$ 

and it is a non-terminating and recurring decimal number.

(iii)  $ \mathbf{{4}\dfrac{ {1}}{ {8}}}$

Ans: $4\dfrac{1}{8}=4+\dfrac{1}{8}=\dfrac{32+1}{8}=\dfrac{33}{8}$

Divide $33$ by $8$.

$\,\,\,\,\,{4.125}$

$8 {\overline{)\;33\quad}}$

$\underline{\,\,\,\,-32\quad}$

$\,\,\,\,\,\,\,\,\,\,\,\,10$

$\underline{\;\;\,\,\,\,-8\quad}$

$\;\;\,\,\,\,\,\,\,\,\,\,\,20$

$\underline{\,\,\,\,\,\,\,\,\,-16}$

$\;\quad\quad\,\,\,\,40$

$\quad\underline{\quad\,\,-40\quad}$

$\quad\underline{\quad\,\, \,\,\,\,0\quad}$

Notice that, after dividing $33$ by $8$, the remainder is found as $0$.

So, $4\dfrac{1}{8}=4.125$ and it is a terminating decimal number.

(iv)  $\mathbf{\dfrac{ {3}}{ {13}}}$

Ans: Divide $3$ by $13$.

$\quad \,\,{0.230769}$

$13 {\overline{)\;3\quad}}$

$\underline{\quad-0\quad}$

$\quad\quad 30$

$\underline{\;\,\quad-26\quad}$

$\;\quad\quad\,\,\,40$

$\underline{\quad\quad\,\,-39\quad}$

$\;\quad\quad\quad\;10$

$\quad\underline{\quad\quad -0\quad}$

$\quad{\quad\quad \quad 100}$

$\quad\quad\underline{\quad \,\, -91\quad}$

$\quad\quad \quad \,\,\,\quad90$

$\quad\quad\underline{\quad\,\,\,\,\,-78\quad}$

$\quad\quad\quad\quad \quad 120$

$\quad \quad\underline{\quad\quad\,\,-117\quad}$

$\quad\quad\underline{\quad \quad\quad\,\, 3\quad}$

It is observed that while dividing $3$ by $13$, the remainder is found as $3$ and that is repeated after each $6$ continuous divisions.

So, $\dfrac{3}{13}=0.230769.......$ or

$\dfrac{3}{13}=0.\overline{230769}$ 

and it is a non-terminating and recurring decimal number.

(v)   $\mathbf{\dfrac{ {2}}{ {11}}}$

Ans: Divide $2$ by $11$.

$\quad \,\,{0.1818}$

$11 {\overline{)\;2\quad}}$

$\underline{\quad-0\quad}$

$\quad\quad20$

$\underline{\quad\;-11\quad}$

$\quad\quad \;\,90$

$\underline{\quad\,\,\,\, -88\;}$

$\;\quad\quad\;20$

$\quad\underline{\quad-11\quad}$

$\quad{\quad\quad  90}$

$\quad\underline{\,\,\quad -88}$

$\quad\quad\quad\,\,2\quad$

It can be noticed that while dividing $2$ by $11$, the remainder is obtained as $2$ and then $9$, and these two numbers are repeated infinitely as remainders.

So, $\dfrac{2}{11}=0.1818.....$ or 

$\dfrac{2}{11}=0.\overline{18}$ 

and it is a non-terminating and recurring decimal number.

(vi) $\mathbf{\dfrac{ {329}}{ {400}}}$

Ans: Divide $329$ by $400$.

$\quad \quad{0.8225}$

$400 {\overline{)\;329\quad}}$

$\underline{\quad\,\,-0\quad}$

$\quad\quad3290$

$\underline{\quad\;-3200\quad}$

$\quad\quad\quad\;900$

$\underline{\quad\quad\quad-800\;}$

$\quad\quad\quad\quad\;1000$

$\quad\underline{\quad\quad\quad-800\quad}$

$\quad{\quad\quad\quad\quad\,\,2000}$

$\quad\underline{\quad\quad\quad\quad-2000\quad}$

$\quad\underline{\quad\quad\quad\quad\,\,\,\,\,\, 0 \quad}$

It can be seen that while dividing $329$ by $400$, the remainder is obtained as $0$.

So, $\dfrac{329}{400}=0.8225$ and is a terminating decimal number.

2. You know that $\dfrac{ {1}}{ {7}} {=0} {.142857}...$. Can you predict what the decimal expansions of $\dfrac{ {2}}{ {7}} {,}\dfrac{ {3}}{ {7}} {,}\dfrac{ {4}}{ {7}} {,}\dfrac{ {5}}{ {7}} {,}\dfrac{ {6}}{ {7}}$  are, without actually doing the long division? If so, how?

$\text{[}$Hint: Study the remainders while finding the value of $\dfrac{ {1}}{ {7}}$ carefully.$\text{]}$

Ans: Note that,  $\dfrac{2}{7},\dfrac{3}{7},\dfrac{4}{7},\dfrac{5}{7}$ and $\dfrac{6}{7}$ can be rewritten as $2\times \dfrac{1}{7},\text{ 3}\times \dfrac{1}{7},\text{ 4}\times \dfrac{1}{7},\text{ 5}\times \dfrac{1}{7},$ and $6\times \dfrac{1}{7}$

Substituting the value of $\dfrac{1}{7}=0.142857$ , gives 

$2 \times \dfrac{1}{7} = 2\times 0.142857...=0.285714...$

$ 3\times \dfrac{1}{7} = 3\times .428571…= .428571...$

\[4\times \dfrac{1}{7}=4\times 0.142857...\]\[\text{=}\,\text{0}\text{.571428}...\]

$5\times \dfrac{1}{7}=5\times 0.71425...$  \[\text{=}\,\text{0}\text{.714285}...\]

$6\times \dfrac{1}{7}=6\times 0.142857...$\[\text{=}\,\text{0}\text{.857142}...\]

So, the values of $\dfrac{2}{7},\text{ }\dfrac{3}{7},\text{ }\dfrac{4}{7},\text{ }\dfrac{5}{7}$ and $\dfrac{6}{7}$ obtained without performing long division are

\[\dfrac{2}{7}=0.\overline{285714}\]

$\dfrac{3}{7}=0.\overline{428571}$

$\dfrac{4}{7}=0.\overline{571428}$

\[\dfrac{5}{7}=0.\overline{714285}\]

$\dfrac{6}{7}=0.\overline{857142}$

3. Express the following in the form \[\dfrac{ {p}}{ {q}}\], where $ {p}$ and $ {q}$ are integers and $ {q}\ne  {0}$.

(i) $\mathbf{ {0} {.}\overline{ {6}}}$

Ans: Let $x=0.\overline{6}$  

 $\Rightarrow x=0.6666$                                                   ….… (1)

 Multiplying both sides of the equation (1) by $10$, gives

$10x=0.6666\times 10$

$10x=6.6666$…..                 …… (2)

Subtracting the equation $\left( 1 \right)$ from $\left( 2 \right)$, gives

$ 10x=6.6666..... $

$ \underline{-x=0.6666.....} $

$  9x=6 $ 

$  9x=6 $

$  x=\dfrac{6}{9}=\dfrac{2}{3} $ 

So, the decimal number becomes

$0.\overline{6}=\dfrac{2}{3}$  and it is in the required  $\dfrac{p}{q}$ form.

(ii) $\mathbf{ {0} {.}\overline{ {47}}}$

Ans: Let  $x=0.\overline{47}$

$\text{   }\Rightarrow x=0.47777.....$                                             ……(a)

Multiplying both sides of the equation (a) by $10$, gives

$10x=4.7777.....$         ……(b)

Subtracting the equation $\left( a \right)$ from $\left( b \right)$, gives

$ 10x=4.7777..... $

$  \underline{-x=0.4777.....} $

$  9x=4.3 $

Therefore,

$x=\dfrac{4.3}{9}\times \dfrac{10}{10} $ 

$ \Rightarrow x=\dfrac{43}{90} $

So, the decimal number becomes 

$0.\overline{47}=\dfrac{43}{90}$  and it is in the required $\dfrac{p}{q}$ form.

(iii) $ \mathbf{{0} {.}\overline{ {001}}}$

Ans: Let $x=0.\overline{001} $           …… (1)

Since the number of recurring decimal number is $3$, so multiplying both sides of the equation (1) by $1000$, gives

$1000\times x=1000\times 0.001001.....$ …… (2)

Subtracting the equation (1) from (2) gives

$ 1000x=1.001001..... $

$  \underline{\text{    }-x=0.001001.....} $

$  999x=1 $

$\Rightarrow x=\dfrac{1}{999}$

Hence, the decimal number becomes 

$0.\overline{001}=\dfrac{1}{999}$ and it is in the $\dfrac{p}{q}$ form.

4. Express $ {0} {.99999}.....$ in the form of $\dfrac{ {p}}{ {q}}$ . Are you surprised by your answer? With your teacher and classmates, discuss why the answer makes sense.

Ans:

Let $x=0.99999.....$                                                             ....... (a)

Multiplying by $10$ both sides of the equation (a), gives

$10x=9.9999.....$                                                             …… (b)

Now, subtracting the equation (a) from (b), gives

$ 10x=9.99999..... $

$  \underline{\,-x=0.99999.....} $

$  9x=9 $ 

$\Rightarrow x=\dfrac{9}{9}$

$\Rightarrow x=1$.

So, the decimal number becomes

$0.99999...=\dfrac{1}{1}$ which is in the $\dfrac{p}{q}$ form.

Yes, for a moment we are amazed by our answer, but when we observe that $0.9999.........$ is extending infinitely, then the answer makes sense.

Therefore, there is no difference between $1$ and $0.9999.........$ and hence these two numbers are equal.

5. What can the maximum number of digits be in the repeating block of digits in the decimal expansion of $\dfrac{ {1}}{ {17}}$ ? Perform the division to check your answer.

Ans: Here the number of digits in the recurring block of $\dfrac{1}{17}$ is to be determined. So, let us calculate the long division to obtain the recurring block of $\dfrac{1}{17}$. Dividing $1$ by $17$ gives

$\quad\quad {0.0588235294117646}$

$17{\overline{)\quad1\quad\quad\quad\quad\quad\quad\quad\quad}}$

$\underline{\quad\,\,\,\,-0\quad}\qquad\qquad\qquad$

$\quad \quad \,\,\,10\qquad\qquad\quad\quad$

$\underline{\quad \quad -0\quad}\qquad\qquad\quad$

$\quad \quad \,\,\,\,\,\;100\qquad\qquad\qquad$

$\underline{\quad \quad \,\,-85\;}\qquad\qquad\quad$

$\quad\qquad\,\,\;150\qquad\qquad\quad$

$\quad\underline{\qquad-136\;}\qquad\qquad\quad$

$\quad{\quad\quad\quad 140}\qquad\qquad\;\;$

$\quad\underline{\qquad-136\quad}\qquad\quad$

${\quad \qquad \,\,\quad 40 \quad}\quad$

$\underline{\qquad \,\,\,\quad -34\;\;}\quad$

$\;\qquad \qquad\,\,60$

$\underline{\qquad \qquad-51}$

$\quad\quad \qquad \quad 90$

$\quad\;\;\underline{\quad \qquad-85}$

$\qquad\quad\;\quad\,\,\,\, 50$

$\quad\quad\;\;\underline{\,\,\quad\,\, -34}$

$\quad\quad\qquad \quad 160$

$\qquad\quad\;\underline{\quad-153}$

$\qquad\qquad\quad\;70$

$\qquad\quad\quad\;\;\underline{-68}$

$\quad\,\,\qquad\qquad 20$

$\qquad\qquad\quad\underline{-17}$

$\qquad\qquad\quad\quad\; 130$

$\qquad\qquad\quad\;\;\underline{-119}$

$\qquad\qquad\qquad\quad 110$

$\qquad\qquad\qquad\;\;\underline{-102}$

$\qquad\qquad\qquad\quad\quad\quad 80$

$\qquad\qquad\qquad\qquad\;\underline{-68}$

$\qquad\qquad\qquad\quad\quad\quad\; 120$

$\qquad\qquad\qquad\qquad\;\;\underline{-119}$

$\qquad\qquad\qquad\quad\quad\quad\; 1$

Thus, it is noticed that while dividing $1$ by $17$, we found $16$ number of digits in the

repeating block of decimal expansion that will continue to be $1$ after going through $16$ continuous divisions.

Hence, it is concluded that $\dfrac{1}{17}=0.0588235294117647.....$ or 

 $\dfrac{1}{17}=0.\overline{0588235294117647}$ and it is a recurring and non-terminating decimal number.

6. Look at several examples of rational numbers in the form $\dfrac{ {p}}{ {q}}\left(  {q}\ne  {0} \right)$, where $ {p}$ and $ {q}$ are integers with no common factors other than $ {1}$ and having terminating decimal representations (expansions). Can you guess what property $ {q}$ must satisfy?

Ans: Let us consider the examples of such rational numbers $\dfrac{5}{2},\dfrac{5}{4},\dfrac{2}{5},\dfrac{2}{10},\dfrac{5}{16}$ of the form $\dfrac{p}{q}$ which have terminating decimal representations.

$ \dfrac{5}{2}=2.5 $

$ \dfrac{5}{4}=1.25 $ 

$ \dfrac{2}{5}=0.4 $

$ \dfrac{2}{10}=0.2 $

$ \dfrac{5}{16}=0.3125 $

In each of the above examples, it can be noticed that the denominators of the rational numbers have powers of $2,5$ or both.

So, $q$ must satisfy the form either ${{2}^{m}}$, or ${{5}^{n}}$, or  both ${{2}^{m}}\times {{5}^{n}}$ (where $m=0,1,2,3.....$ and $n=0,1,2,3.....$) in the form of $\dfrac{p}{q}$.

7. Write three numbers whose decimal expansions are non-terminating non-recurring.

Ans: All the irrational numbers are non-terminating and non-recurring, because irrational numbers do not have any representations of the form of $\dfrac{p}{q}$ $\left( q\ne 0 \right)$, where $p$ and $q$are integers. For example: 

$\sqrt{2}=1.41421.....$,

$\sqrt{3}=1.73205...$

$\sqrt{7}=2.645751....$

are the numbers whose decimal representations are non-terminating and non-recurring.

8. Find any three irrational numbers between the rational numbers $\dfrac{ {5}}{ {7}}$ and $\dfrac{ {9}}{ {11}}$.

Ans: Converting  $\dfrac{5}{7}$and $\dfrac{9}{11}$ into the decimal form gives

$\dfrac{5}{7}=0.714285.....$ and 

$\dfrac{9}{11}=0.818181.....$

Therefore, $3$ irrational numbers that are contained between $0.714285......$ and $0.818181.....$

are:

$ 0.73073007300073...... $ 

$  0.74074007400074...... $ 

$ 0.76076007600076...... $

Hence, three irrational numbers between the rational numbers $\dfrac{5}{7}$ and $\dfrac{9}{11}$ are

$ 0.73073007300073...... $ 

$  0.74074007400074...... $ 

$ 0.76076007600076...... $

9. Classify the following numbers as rational or irrational:

(i) $\mathbf{\sqrt{ {23}}}$

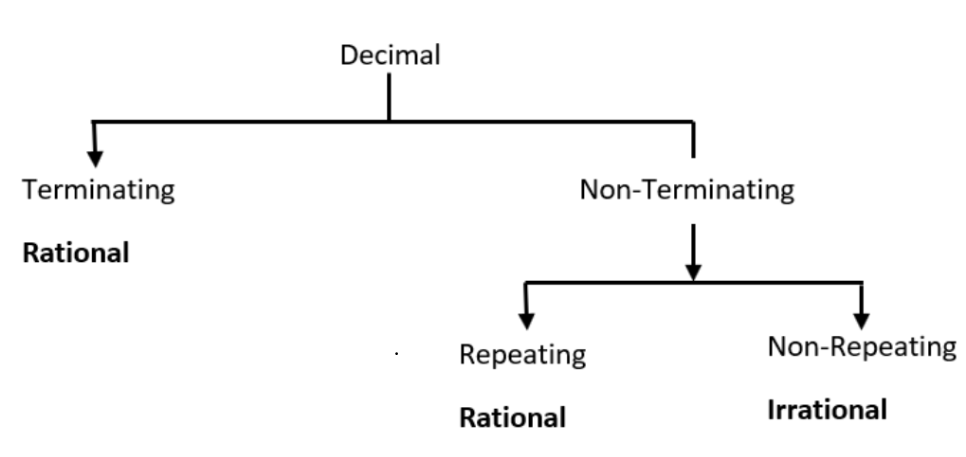
Ans: The following diagram reminds us of the distinctions among the types of rational and irrational numbers.

After evaluating the square root gives

$\sqrt{23}=4.795831.....$ , which is an irrational number.

(ii) $\mathbf{\sqrt{ {225}}}$

Ans: After evaluating the square root gives

$\sqrt{225}=15$, which is a rational number.

That is, $\sqrt{225}$ is a rational number.

(iii) $ \mathbf{{0} {.3796}}$

Ans: The given number is $0.3796$. It is terminating decimal. 

So, $0.3796$ is a rational number.

(iv) $ \mathbf{{7} {.478478}}$

Ans: The given number is \[7.478478\ldots .\] 

It is a non-terminating and recurring decimal that can be written in the $\dfrac{p}{q}$ form.

Let      $x=7.478478\ldots .$                                   ……(a)

Multiplying the equation (a) both sides by $100$ gives

$\Rightarrow 1000x=7478.478478.....$                                               ……(b)

Subtracting the equation (a) from (b), gives

$ 1000x=7478.478478.... $

$  \underline{\text{    }-x=\text{     }7.478478\ldots .} $

$ 999x=7471 $

$ 999x=7471 $

$  \text{      }x=\dfrac{7471}{999} $

Therefore, $7.478478.....=\dfrac{7471}{999}$, which is in the form of $\dfrac{p}{q}$

So, $7.478478...$ is a rational number.

(v) $ \mathbf{{1} {.101001000100001}.....}$

Ans: The given number is \[1.101001000100001....\]

It can be clearly seen that the number \[1.101001000100001....\] is a non-terminating and non-recurring decimal and it is known that non-terminating non-recurring decimals cannot be written in the form of $\dfrac{p}{q}$.

Hence, the number \[1.101001000100001....\] is an irrational number.

Exercise (1.4)

1.  Classify the following numbers as rational or irrational:

(i) $ \mathbf{{2-}\sqrt{ {5}}}$

Ans: The given number is $2-\sqrt{5}$.

Here, $\sqrt{5}=2.236.....$ and it is a non-repeating and non-terminating irrational number.

Therefore, substituting the value of $\sqrt{5}$ gives

$2-\sqrt{5}=2-2.236.....$

$=-0.236.....$, which is an irrational number.

So, $2-\sqrt{5}$ is an irrational number.

(ii) $\mathbf{\left(  {3+}\sqrt{ {23}} \right) {-}\left( \sqrt{ {23}} \right)}$

Ans: The given number is $\left( 3+\sqrt{23} \right)-\left( \sqrt{23} \right)$.

The number can be written as

$\left( 3+\sqrt{23} \right)-\sqrt{23}=3+\sqrt{23}-\sqrt{23} $ 

$  =3 $

$=\dfrac{3}{1}$, which is in the $\dfrac{p}{q}$ form and so, it is a rational number.

Hence, the number $\left( 3+\sqrt{23} \right)-\sqrt{23}$ is a rational number.

(iii) $\mathbf{\dfrac{ {2}\sqrt{ {7}}}{ {7}\sqrt{ {7}}}}$

Ans: The given number is $\dfrac{2\sqrt{7}}{7\sqrt{7}}$.

The number can be written as

$\dfrac{2\sqrt{7}}{7\sqrt{7}}=\dfrac{2}{7}$, which is in the $\dfrac{p}{q}$  form and so, it is a rational number.

Hence, the number  $\dfrac{2\sqrt{7}}{7\sqrt{7}}$ is a rational number.

(iv) $\mathbf{\dfrac{ {1}}{\sqrt{ {2}}}}$

Ans: The given number is $\dfrac{1}{\sqrt{2}}$.

It is known that, $\sqrt{2}=1.414.....$ and it is a non-repeating and non-terminating irrational number.

Hence, the number $\dfrac{1}{\sqrt{2}}$ is an irrational number.

(v) $ \mathbf{{2\pi }}$

Ans: The given number is $2\pi $.

It is known that, $\pi =3.1415$ and it is an irrational number.

Now remember that, Rational $\times $ Irrational = Irrational.

Hence, $2\pi $ is also an irrational number.

2. Simplify each of the of the following expressions:

(i) $\mathbf{\left(  {3+}\sqrt{ {3}} \right)\left(  {2+}\sqrt{ {2}} \right)}$

Ans: The given number is $\left( 3+\sqrt{3} \right)\left( 2+\sqrt{2} \right)$.

By calculating the multiplication, it can be written as

$\left( 3+\sqrt{3} \right)\left( 2+\sqrt{2} \right)=3\left( 2+\sqrt{2} \right)+\sqrt{3}\left( 2+\sqrt{2} \right)$.

\[= 6 + 4 \sqrt{2} + 2 \sqrt{3}+ \sqrt{6}\]

(ii) $\mathbf{\left(  {3+}\sqrt{ {3}} \right)\left(  {3-}\sqrt{ {3}} \right)}$

Ans: The given number is $\left( 3+\sqrt{3} \right)\left( 3-\sqrt{3} \right)$.

By applying the formula $\left( a+b \right)\left( a-b \right)={{a}^{2}}-{{b}^{2}}$, the number can be written as

$\left( 3+\sqrt{3} \right)\left( 3-\sqrt{3} \right)={{3}^{2}}-{{\left( \sqrt{3} \right)}^{2}}=9-3=6$.

(iii)  $\mathbf{{{\left( \sqrt{ {5}} {+}\sqrt{ {2}} \right)}^{ {2}}}}$

Ans: The given number is ${{\left( \sqrt{5}+\sqrt{2} \right)}^{2}}$.

Applying the formula ${{\left( a+b \right)}^{2}}={{a}^{2+}}2ab+{{b}^{2}}$, the number can be written as

${{\left( \sqrt{5}+\sqrt{2} \right)}^{2}}={{\left( \sqrt{5} \right)}^{2}}+2\sqrt{5}\sqrt{2}+{{\left( \sqrt{2} \right)}^{2}}$

 $=5+2\sqrt{10}+2$

 $=7+2\sqrt{10}$.

(iv)  $\mathbf{\left( \sqrt{ {5}}-\sqrt{ {2}} \right)\left( \sqrt{ {5}} {+}\sqrt{ {2}} \right)}$

Ans: The given number is $\left( \sqrt{5}-\sqrt{2} \right)\left( \sqrt{5}+\sqrt{2} \right)$.

Applying the formula $\left( a+b \right)\left( a-b \right)={{a}^{2}}-{{b}^{2}}$, the number can be expressed as

$\left( \sqrt{5}-\sqrt{2} \right)\left( \sqrt{5}+\sqrt{2} \right)={{\left( \sqrt{5} \right)}^{2}}-{{\left( \sqrt{2} \right)}^{2}}$

$=5-2 $

$ =3. $ 

3. Recall that, $ {\pi }$ is defined as the ratio of the circumference (say $ {c}$) of a circle to its diameter (say $ {d}$). That is, $ {\pi =}\dfrac{ {c}}{ {d}}$ .This seems to contradict the fact that $ {\pi }$ is irrational. How will you resolve this contradiction?

Ans: It is known that, $\pi =\dfrac{22}{7}$, which is a rational number. But, note that this value of $\pi $ is an approximation.

On dividing $22$ by $7$, the quotient $3.14...$ is a non-recurring and non-terminating number. Therefore, it is an irrational number.

In order of increasing accuracy, approximate fractions are

$\dfrac{22}{7}$, $\dfrac{333}{106}$, $\dfrac{355}{113}$, $\dfrac{52163}{16604}$, $\dfrac{103993}{33102}$, and \[\dfrac{245850922}{78256779}\].

Each of the above quotients has the value $3.14...$, which is a non-recurring and non-terminating number.

Thus, $\pi $ is irrational.

So, either circumference $\left( c \right)$ or diameter $\left( d \right)$ or both should be irrational numbers.

Hence, it is concluded that there is no contradiction regarding the value of $\pi $ and it is made out that the value of $\pi $ is irrational.

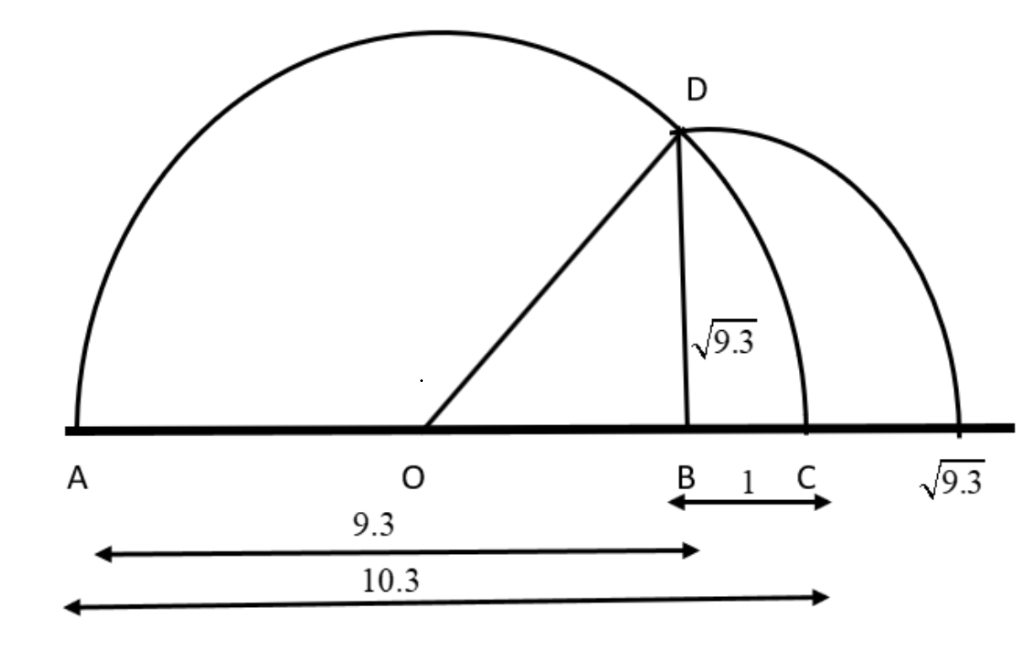
4. Represent $\sqrt{ {9} {.3}}$ on the number line.

Ans: Follow the procedure given below to represent the number $\sqrt{9.3}$.

• First, mark the distance $9.3$ units from a fixed-point $A$ on the number line to get a point $B$. Then $AB=9.3$ units.

• Secondly, from the point $B$ mark a distance of $1$ unit and denote the ending point as $C$.

• Thirdly, locate the midpoint of $AC$ and denote it as $O$.

• Fourthly, draw a semi-circle to the centre $O$ with the radius $OC=5.15$ units. Then 

$ AC=AB+BC $ 

$  =9.3+1 $ 

$  =10.3 $

So, $OC=\dfrac{AC}{2}=\dfrac{10.3}{2}=5.15$.

• Finally, draw a perpendicular line at $B$ and draw an arc to the centre $B$ and then let it meet at the semicircle $AC$ at $D$ as given in the diagram below.

5. Rationalize the denominators of the following:

(i) $\mathbf{\dfrac{ {1}}{\sqrt{ {7}}}}$

Ans: The given number is $\dfrac{1}{\sqrt{7}}$.

Multiplying and dividing by $\sqrt{7}$ to the number gives

$\dfrac{1}{\sqrt{7}}\times \dfrac{\sqrt{7}}{\sqrt{7}}=\dfrac{\sqrt{7}}{7}$.

(ii) $\mathbf{\dfrac{ {1}}{\sqrt{ {7}} {-}\sqrt{ {6}}}}$

Ans: The given number is $\dfrac{1}{\sqrt{7}-\sqrt{6}}$.

Multiplying and dividing by $\sqrt{7}+\sqrt{6}$ to the number gives

$\dfrac{1}{\sqrt{7}-\sqrt{6}}\times \dfrac{\sqrt{7}+\sqrt{6}}{\sqrt{7}+\sqrt{6}}=\dfrac{\sqrt{7}+\sqrt{6}}{\left( \sqrt{7}-\sqrt{6} \right)\left( \sqrt{7}+\sqrt{6} \right)}$

Now, applying the formula $\left( a-b \right)\left( a+b \right)={{a}^{2}}-{{b}^{2}}$ to the denominator gives

$ \dfrac{1}{\sqrt{7}-\sqrt{6}}=\dfrac{\sqrt{7}+\sqrt{6}}{{{\left( \sqrt{7} \right)}^{2}}-{{\left( \sqrt{6} \right)}^{2}}} $ 

$ =\dfrac{\sqrt{7}+\sqrt{6}}{7-6} $ 

$  =\dfrac{\sqrt{7}+\sqrt{6}}{1}. $

(iii) $\mathbf{\dfrac{ {1}}{\sqrt{ {5}} {+}\sqrt{ {2}}}}$

Ans: The given number is $\dfrac{1}{\sqrt{5}+\sqrt{2}}$.

Multiplying and dividing by $\sqrt{5}-\sqrt{2}$ to the number gives

$\dfrac{1}{\sqrt{5}+\sqrt{2}}\times \dfrac{\sqrt{5}-\sqrt{2}}{\sqrt{5}-\sqrt{2}}=\dfrac{\sqrt{5}-\sqrt{2}}{\left( \sqrt{5}+\sqrt{2} \right)\left( \sqrt{5}-\sqrt{2} \right)}$

Now, applying the formula $\left( a+b \right)\left( a-b \right)={{a}^{2}}-{{b}^{2}}$  to the denominator gives

$ \dfrac{1}{\sqrt{5}+\sqrt{2}}=\dfrac{\sqrt{5}-\sqrt{2}}{{{\left( \sqrt{5} \right)}^{2}}-{{\left( \sqrt{2} \right)}^{2}}} $ 

$ =\dfrac{\sqrt{5}-\sqrt{2}}{5-2} $

$ =\dfrac{\sqrt{5}-\sqrt{2}}{3}. $ 

(iv) $\mathbf{\dfrac{ {1}}{\sqrt{ {7}} {-2}}}$

Ans: The given number is $\dfrac{1}{\sqrt{7}-2}$.

Multiplying and dividing by $\sqrt{7}+2$ to the number gives

$\dfrac{1}{\sqrt{7}-2}=\dfrac{\sqrt{7}+2}{\left( \sqrt{7}-2 \right)\left( \sqrt{7}+2 \right)}\\$.

Now, applying the formula $\left( a+b \right)\left( a-b \right)={{a}^{2}}-{{b}^{2}}$ to the denominator gives

$ \dfrac{1}{\sqrt{7}-2}=\dfrac{\sqrt{7}+2}{{{\left( \sqrt{7} \right)}^{2}}-{{\left( 2 \right)}^{2}}} $

$ =\dfrac{\sqrt{7}+2}{7-4} $ 

$  =\dfrac{\sqrt{7}+2}{3}. $

Exercise (1.5)

1. Compute the value of each of the following expressions:

(i) $\mathbf{ {6}{{ {4}}^{\dfrac{ {1}}{ {2}}}}}$

Ans: The given number is \[{{64}^{\dfrac{1}{2}}}\].

By the laws of indices,

${{a}^{\dfrac{m}{n}}}=\sqrt[n]{{{a}^{m}}}$, where$a>0$.

Therefore,

$ {{64}^{\dfrac{1}{2}}}=\sqrt[2]{64} $

$  =\sqrt[2]{8\times \text{8}} $

$  =8. $

Hence, the value of ${{64}^{\dfrac{1}{2}}}$ is $8$.

(ii) $ \mathbf{{3}{{ {2}}^{\dfrac{ {1}}{ {5}}}}}$

Ans: The given number is ${{32}^{\dfrac{1}{5}}}$.

By the laws of indices,

${{a}^{\dfrac{m}{n}}}=\sqrt[m]{{{a}^{m}}}$, where $a>0$

$ {{32}^{\dfrac{1}{5}}}=\sqrt[5]{32}$

$ =\sqrt[5]{2\times 2\times 2\times 2\times 2} $ 

$ =\sqrt[5]{{{2}^{5}}} $

$ =2. $

Alternative Method:

By the law of indices ${{\left( {{a}^{m}} \right)}^{n}}={{a}^{mn}}$, then it gives

$ {{32}^{\dfrac{1}{5}}}={{(2\times 2\times 2\times 2\times 2)}^{\dfrac{1}{5}}}$ 

$ ={{\left( {{2}^{5}} \right)}^{\dfrac{1}{5}}} $

$ ={{2}^{\dfrac{5}{5}}} $

$=2. $

Hence, the value of the expression ${{32}^{\dfrac{1}{5}}}$ is $2$.

(iii) $\mathbf{{12}{{ {5}}^{\dfrac{ {1}}{ {5}}}}}$

Ans: The given number is ${{125}^{\dfrac{1}{3}}}$.

By the laws of indices

${{a}^{\dfrac{m}{n}}}=\sqrt[n]{{{a}^{m}}}$ where$a>0$.

Therefore,

$ {{125}^{\dfrac{1}{3}}}=\sqrt[3]{125} $

$  =\sqrt[3]{5\times 5\times 5} $

$  =5. $

Hence, the value of the expression ${{125}^{\dfrac{1}{3}}}$ is $5$.

2. Compute the value of each of the following expressions:

(i) $\mathbf{{{ {9}}^{\dfrac{ {3}}{ {2}}}}}$

Ans: The given number is ${{9}^{\dfrac{3}{2}}}$.

By the laws of indices,

 ${{a}^{\dfrac{m}{n}}}=\sqrt[n]{{{a}^{m}}}$ where $a>0$.

Therefore,

$ {{9}^{\dfrac{3}{2}}}=\sqrt[2]{{{\left( 9 \right)}^{3}}} $

$  =\sqrt[2]{9\times 9\times 9} $

$ =\sqrt[2]{3\times 3\times 3\times 3\times 3\times 3} $

$=3\times 3\times 3 $

$ =27. $

Alternative Method:

By the laws of indices, ${{\left( {{a}^{m}} \right)}^{n}}={{a}^{mn}}$, then it gives

$ {{9}^{\dfrac{3}{2}}}={{\left( 3\times 3 \right)}^{\dfrac{3}{2}}}$

$  ={{\left( {{3}^{2}} \right)}^{\dfrac{3}{2}}} $

$  ={{3}^{2\times \dfrac{3}{2}}} $

$ ={{3}^{3}} $

That is,

${{9}^{\dfrac{3}{2}}}=27.$

Hence, the value of the expression ${{9}^{\dfrac{3}{2}}}$ is $27$.

(ii) $\mathbf{{3}{{ {2}}^{\dfrac{ {2}}{ {5}}}}}$

Ans: We know that ${{a}^{\dfrac{m}{n}}}=\sqrt[n]{{{a}^{m}}}$ where $a>0$.

We conclude that ${{32}^{\dfrac{2}{5}}}$ can also be written as

$ \sqrt[5]{{{\left( 32 \right)}^{2}}}=\sqrt[5]{\left( 2\times 2\times 2\times 2\times 2 \right)\times \left( 2\times 2\times 2\times 2\times 2 \right)} $ 

$  =2\times 2 $

$ =4 $ 

Therefore, the value of ${{32}^{\dfrac{2}{5}}}$ is $4$.

(iii) $\mathbf{{1}{{ {6}}^{\dfrac{ {3}}{ {4}}}}}$

Ans: The given number is ${{16}^{\dfrac{3}{4}}}$.

By the laws of indices, 

${{a}^{\dfrac{m}{n}}}=\sqrt[n]{{{a}^{m}}}$, where $a>0$.

Therefore,

$ {{16}^{\dfrac{3}{4}}}=\sqrt[4]{{{\left( 16 \right)}^{3}}} $

$  =\sqrt[4]{\left( 2\times 2\times 2\times 2 \right)\times \left( 2\times 2\times 2\times 2 \right)\times \left( 2\times 2\times 2\times 2 \right)} $

$  =2\times 2\times 2 $

$  =8. $

Hence, the value of the expression ${{16}^{\dfrac{3}{4}}}$ is $8$.

Alternative Method:

By the laws of indices,

${{({{a}^{m}})}^{n}}={{a}^{mn}}$, where $a>0$.

Therefore,

$ {{16}^{\dfrac{3}{4}}}={{(4\times 4)}^{\dfrac{3}{4}}} $

$  ={{({{4}^{2}})}^{\dfrac{3}{4}}} $ 

$ ={{(4)}^{2\times \dfrac{3}{4}}} $

$ ={{({{2}^{2}})}^{2\times \dfrac{3}{4}}} $ 

$ ={{2}^{2\times 2\times \dfrac{3}{4}}} $

$ ={{2}^{3}} $

$ =8. $

Hence, the value of the expression is ${{16}^{\dfrac{3}{4}}}=8$.

(iv) $\mathbf{{12}{{ {5}}^{ {-}\dfrac{ {1}}{ {3}}}}}$

Ans: The given number is ${{125}^{-\dfrac{1}{3}}}$.

By the laws of indices, it is known that 

${{a}^{-n}}=\dfrac{1}{{{a}^{^{n}}}}$, where $a>0$.

Therefore, 

$ {{125}^{-\dfrac{1}{3}}}=\dfrac{1}{{{125}^{\dfrac{1}{3}}}} $

$  ={{\left( \dfrac{1}{125} \right)}^{\dfrac{1}{3}}} $

$ =\sqrt[3]{\left( \dfrac{1}{125} \right)} $

$ =\sqrt[3]{\left( \dfrac{1}{5}\times \dfrac{1}{5}\times \dfrac{1}{5} \right)} $

$ =\dfrac{1}{5}. $

Hence, the value of the expression ${{125}^{-\dfrac{1}{3}}}$ is  $\dfrac{1}{5}$.

3. Simplify and evaluate each of the expressions:

(i)$\mathbf{{{ {2}}^{\dfrac{ {2}}{ {3}}}} {.}{{ {2}}^{\dfrac{ {1}}{ {5}}}}}$

Ans: The given expression is ${{2}^{\dfrac{2}{3}}}{{.2}^{\dfrac{1}{5}}}$.

By the laws of indices, it is known that

${{a}^{m}}\cdot {{a}^{n}}={{a}^{m+n}}$, where $a>0$.

Therefore,

 ${{2}^{\dfrac{2}{3}}}{{.2}^{\dfrac{1}{5}}}={{(2)}^{\dfrac{2}{3}+\dfrac{1}{5}}}$

 $ ={{(2)}^{\dfrac{10+3}{15}}} $

 $ ={{2}^{\dfrac{13}{15}}}. $

Hence, the value of the expression ${{2}^{\dfrac{2}{3}}}{{.2}^{\dfrac{1}{5}}}$ is ${{2}^{\dfrac{13}{15}}}$.

(ii) ${{\left( {{\frac{ {1}}{ {{3}^3}}}} \right)}^{ {7}}}$

Ans: The given expression is  ${{\left( {{\frac{ {1}}{ {{3}^3}}}} \right)}^{ {7}}}$.

It is known by the laws of indices that,

 ${{({{a}^{m}})}^{n}}={{a}^{mn}}$, where $a>0$.

Therefore,

 ${{\left( {{\frac{ {1}}{ {{3}^3}}}} \right)}^{ {7}}} =\left ( \dfrac{1}{3^{21}} \right )$

Hence, the value of the expression  ${{\left( {{\frac{ {1}}{ {{3}^3}}}} \right)}^{ {7}}}$ is  $\left ( \dfrac{1}{3^{21}} \right )$

(iii) $\dfrac{ {1}{{ {1}}^{\dfrac{ {1}}{ {2}}}}}{ {1}{{ {1}}^{\dfrac{ {1}}{ {4}}}}}$

Ans: The given number is $\dfrac{{{11}^{\dfrac{1}{2}}}}{{{11}^{\dfrac{1}{4}}}}$.

It is known by the Laws of Indices that

 $\dfrac{{{a}^{m}}}{{{a}^{n}}}={{a}^{m-n}}$, where $a>0$.

Therefore,

$\dfrac{{{11}^{\dfrac{1}{2}}}}{{{11}^{\dfrac{1}{4}}}}={{11}^{\dfrac{1}{2}-\dfrac{1}{4}}} $

$ ={{11}^{\dfrac{2-1}{4}}} $ 

$  ={{11}^{\dfrac{1}{4}}}. $

Hence, the value of the expression $\dfrac{{{11}^{\dfrac{1}{2}}}}{{{11}^{\dfrac{1}{4}}}}$ is  ${{11}^{\dfrac{1}{4}}}$.

(iv) $\mathbf{{{ {7}}^{\dfrac{ {1}}{ {2}}}} {.}{{ {8}}^{\dfrac{ {1}}{ {2}}}}}$

Ans: The given expression is ${{7}^{\dfrac{1}{2}}}\cdot {{8}^{\dfrac{1}{2}}}$.

It is known by the Laws of Indices that

${{a}^{m}}\cdot {{b}^{m}}={{(a\cdot b)}^{m}}$, where $a>0$.

Therefore,

$ {{7}^{\dfrac{1}{2}}}\cdot {{8}^{\dfrac{1}{2}}}={{(7\times 8)}^{\dfrac{1}{2}}} $  $={{(56)}^{\dfrac{1}{2}}}. $

Hence, the value of the expression ${{7}^{\dfrac{1}{2}}}\cdot {{8}^{\dfrac{1}{2}}}$ is ${{(56)}^{\dfrac{1}{2}}}$.

Class 9 Maths Chapter 1 Solutions - Free PDF Download

The NCERT Solutions for Class 9 Maths Chapter 1, "Number Systems," serve as the first chapter of the Class 9 Maths curriculum. This chapter provides an in-depth discussion on Number Systems and their applications, starting with an introduction to whole numbers, integers, and rational numbers.

The chapter begins with an overview of Number Systems in section 1.1, followed by two crucial topics in sections 1.2 and 1.3:

1. Irrational Numbers: These are numbers that cannot be expressed in the form p/q.

2. Real Numbers and their Decimal Expansions: This section examines the decimal expansions of real numbers to differentiate between rational and irrational numbers.

Further, the chapter covers:

• Representing Real Numbers on the Number Line: Solutions for two problems in Exercise 1.4 are provided.

• Operations on Real Numbers: This section explores operations such as addition, subtraction, multiplication, and division involving irrational numbers.

• Laws of Exponents for Real Numbers: These laws are used to solve various questions.

NCERT Solutions for Class 9 Maths Chapter 1 All Exercise

Conclusion

The class 9 maths chapter 1 PDF solutions by Vedantu provide a detailed and clear explanation of the concepts in the chapter. This chapter covers important topics like rational and irrational numbers, real numbers, and their decimal expansions. Understanding these foundational concepts is crucial for success in higher-level maths. When studying, focus on grasping the properties of different types of numbers and practising their operations. The solutions by Vedantu simplify these concepts with step-by-step explanations, making them easier to understand. In previous year question papers, typically 3 to 5 questions from this chapter are asked. These questions often test your understanding of number classification, representation of numbers on the number line, and converting between different forms of numbers. Therefore, practice is key to mastering this chapter and performing well in exams.

Other Related Links for CBSE Class 9 Maths Chapter 1

Chapter-Specific NCERT Solutions for Class 9 Maths

Given below are the chapter-wise NCERT Solutions for Class 9 Maths. Go through these chapter-wise solutions to be thoroughly familiar with the concepts.

Important Study Materials for CBSE Class 9 Maths