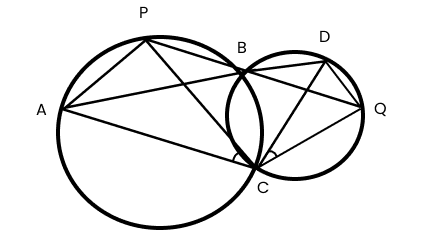
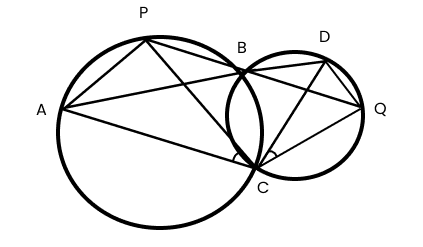
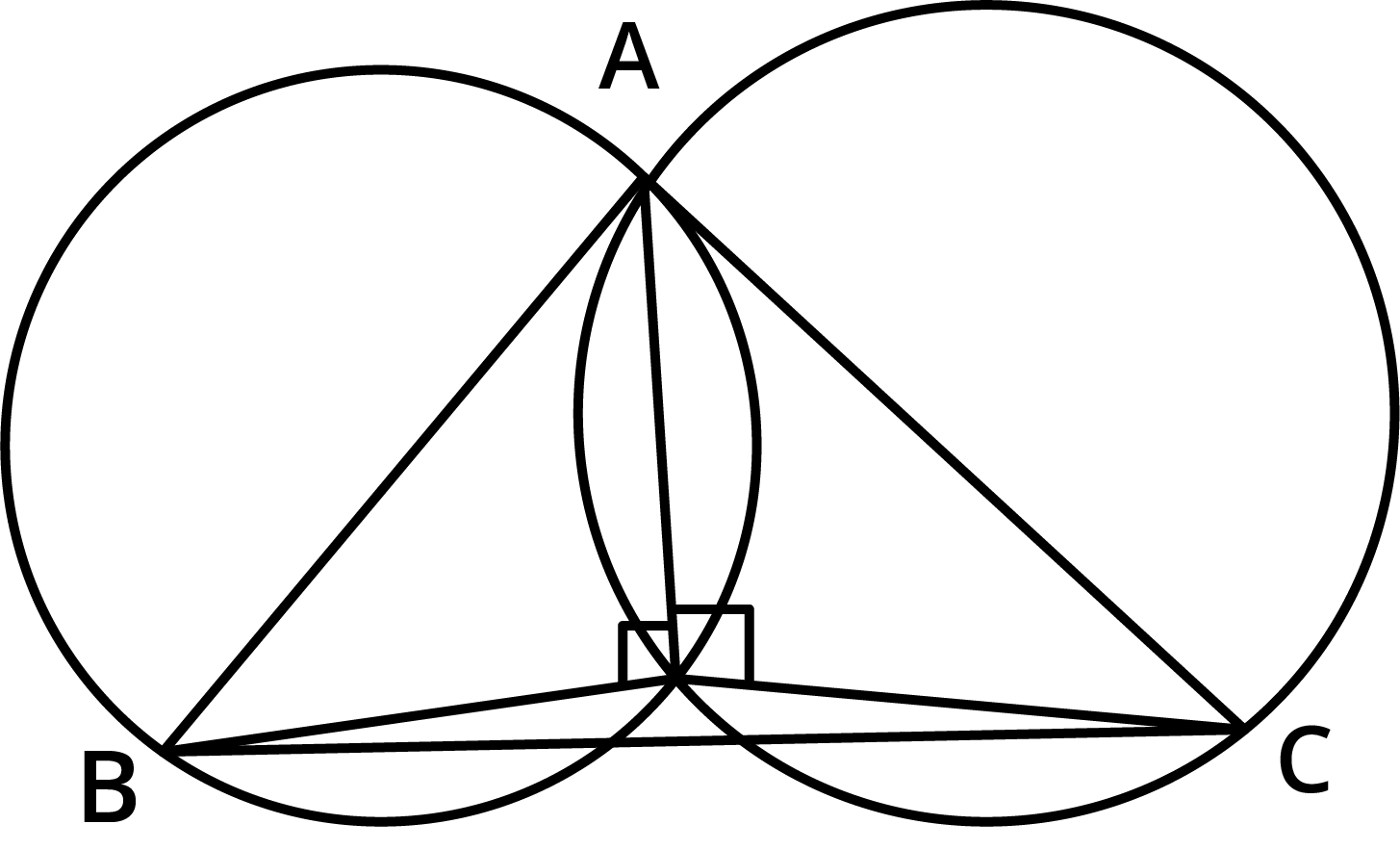
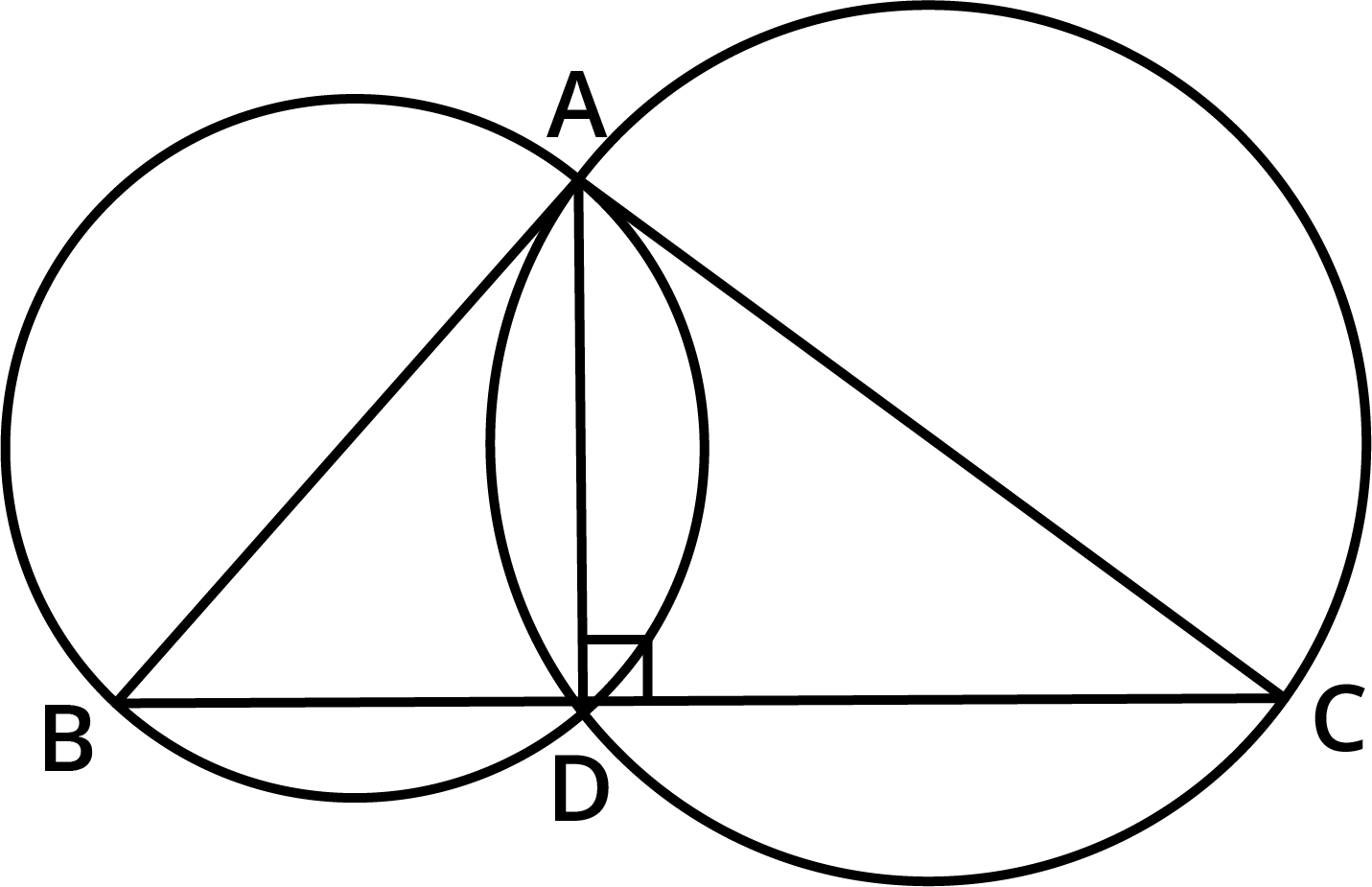
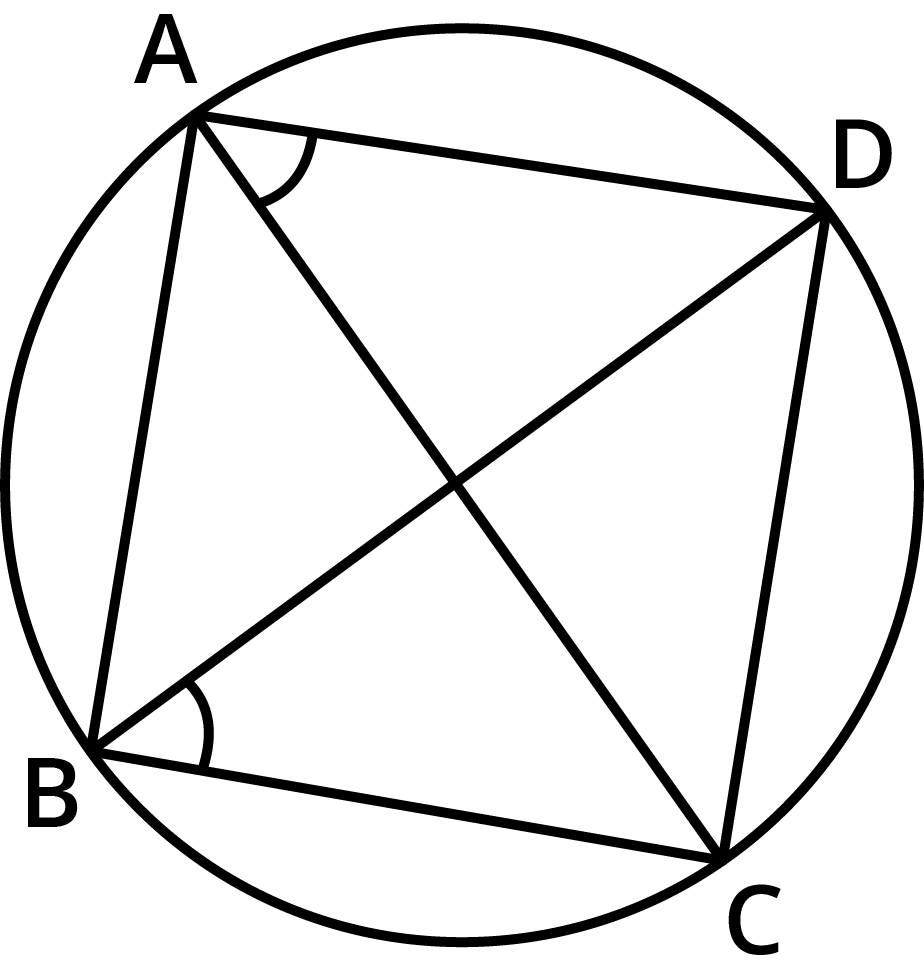
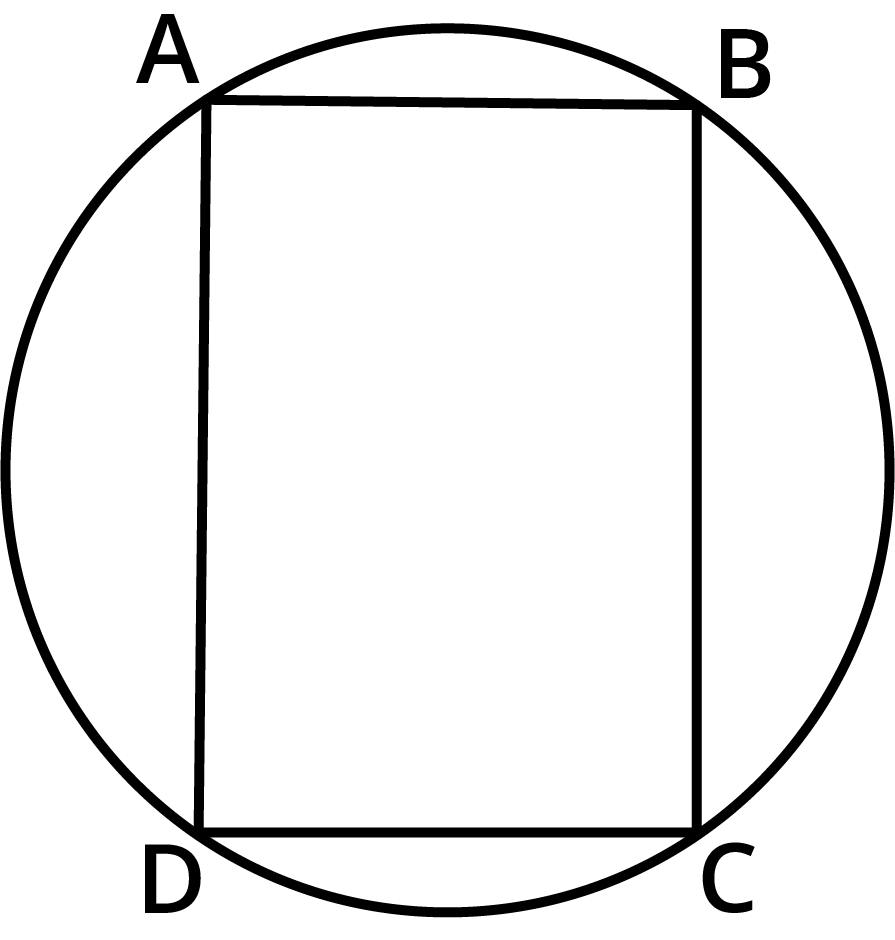
Master Vedantu's Class 9 Maths Chapter 9 Exercise 9.3 Solutions With Expert Guidance
NCERT Solutions For Class 9 Maths Chapter 9 Circles
FAQs on NCERT Solutions For Class 9 Maths Chapter 9 Circles
1. What are the key theorems used to solve questions in the NCERT Solutions for Class 9 Maths Chapter 9, Circles?
The NCERT Solutions for Chapter 9 primarily rely on a set of core theorems. Key ones include:
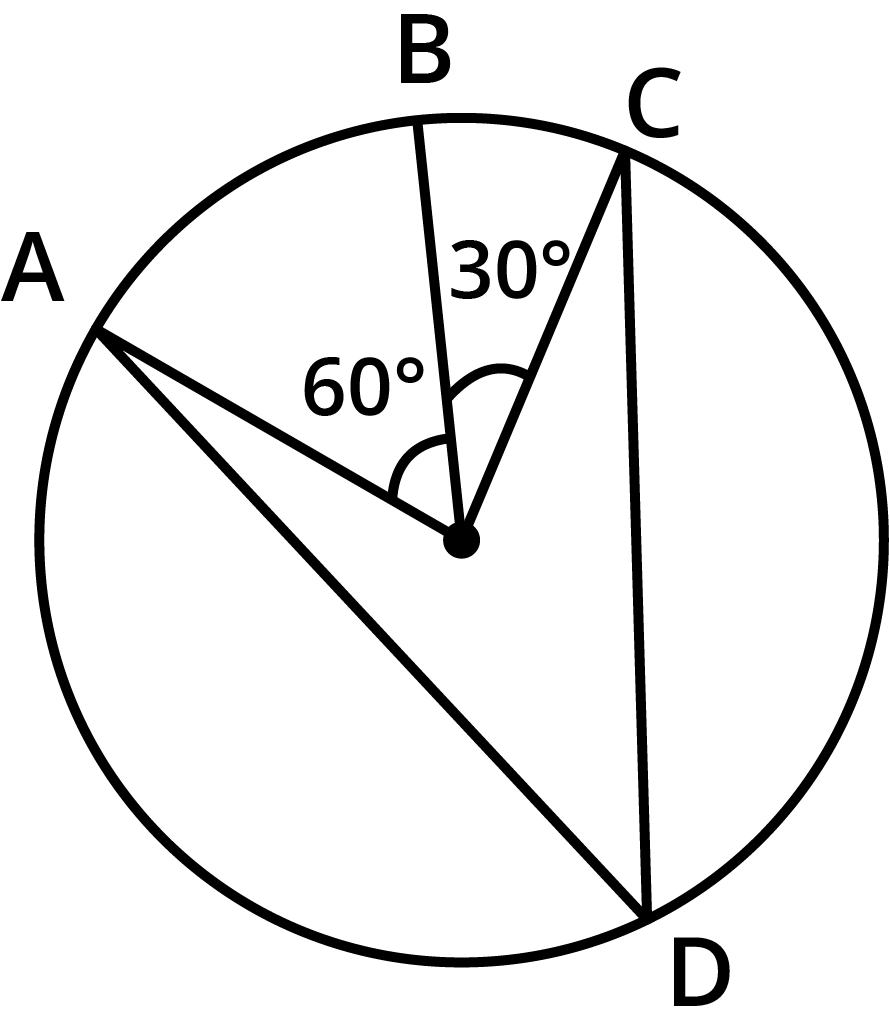
- Equal chords of a circle subtend equal angles at the centre.
- The perpendicular from the centre of a circle to a chord bisects the chord.
- There is one and only one circle passing through three given non-collinear points.
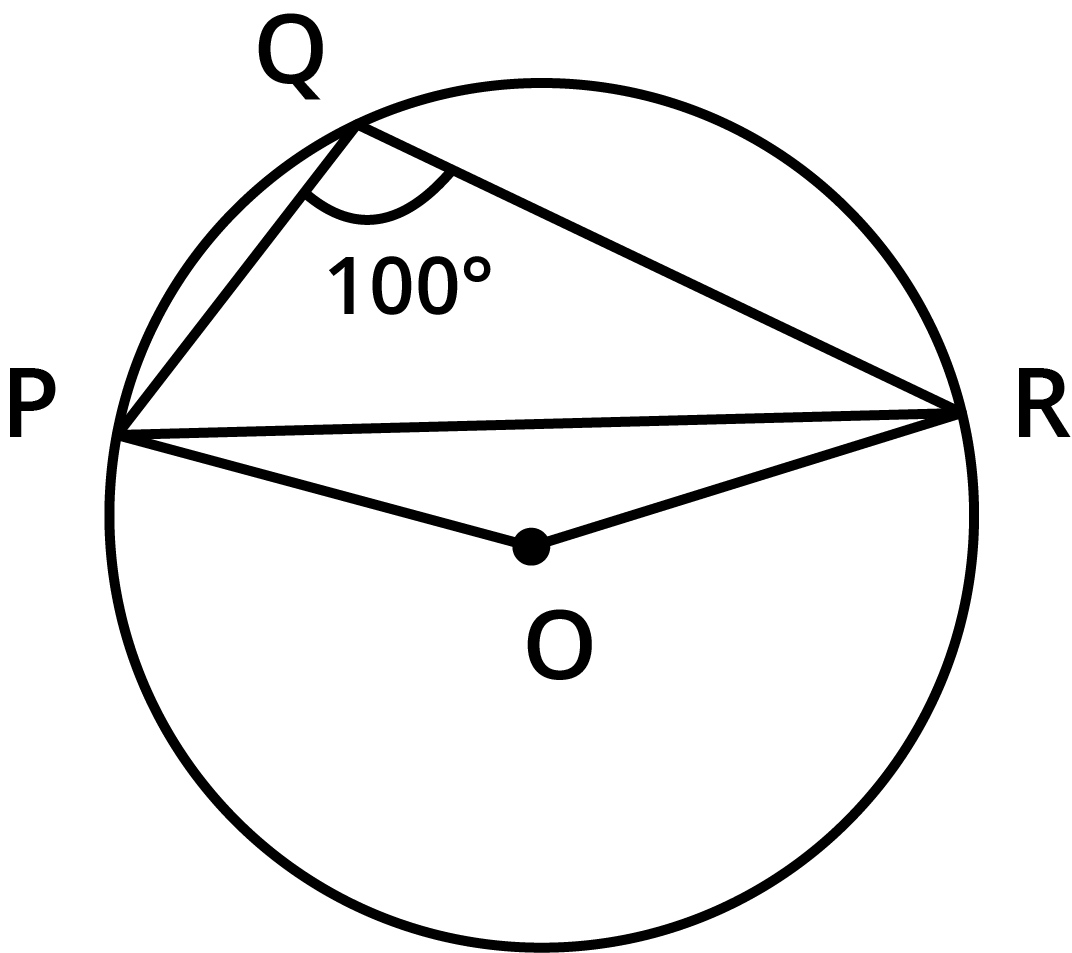
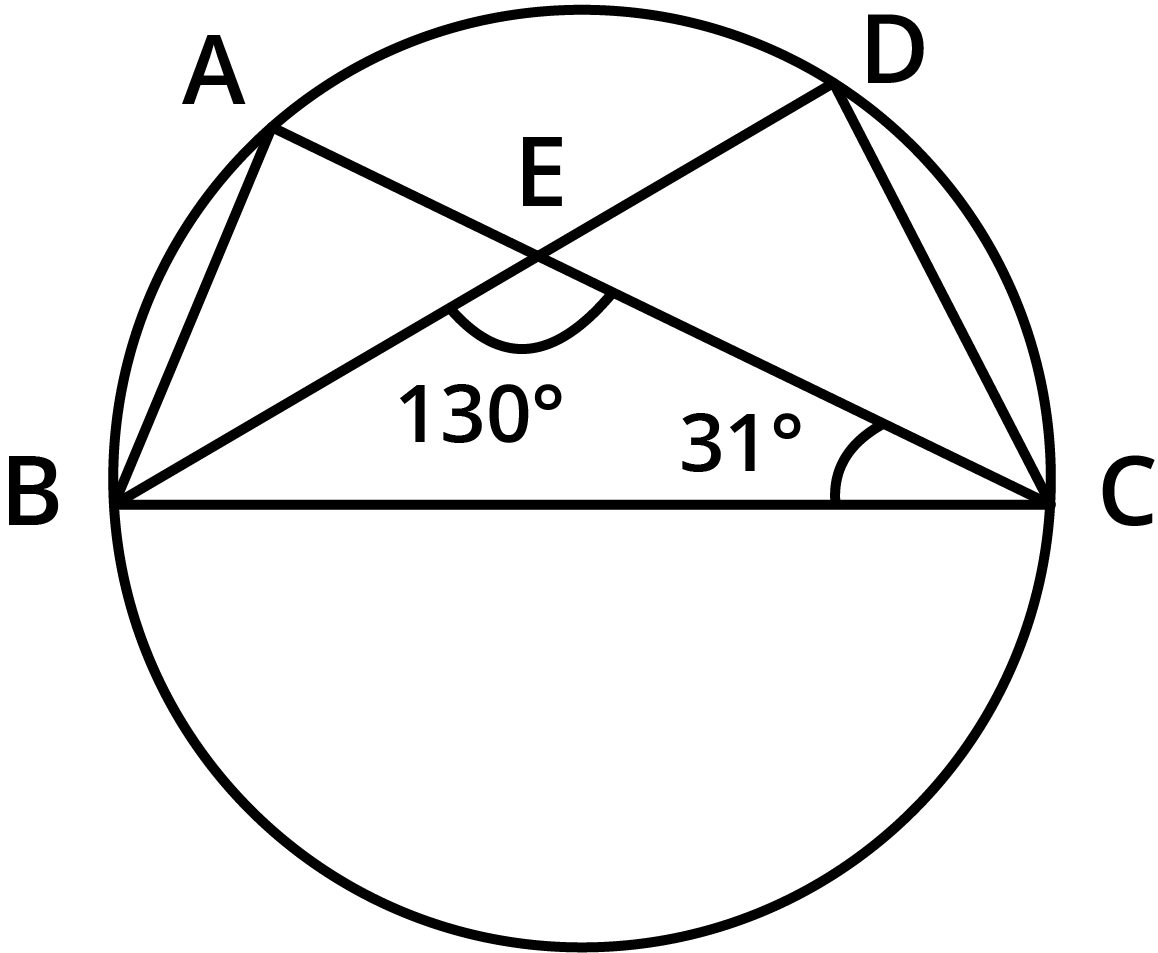
- The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.
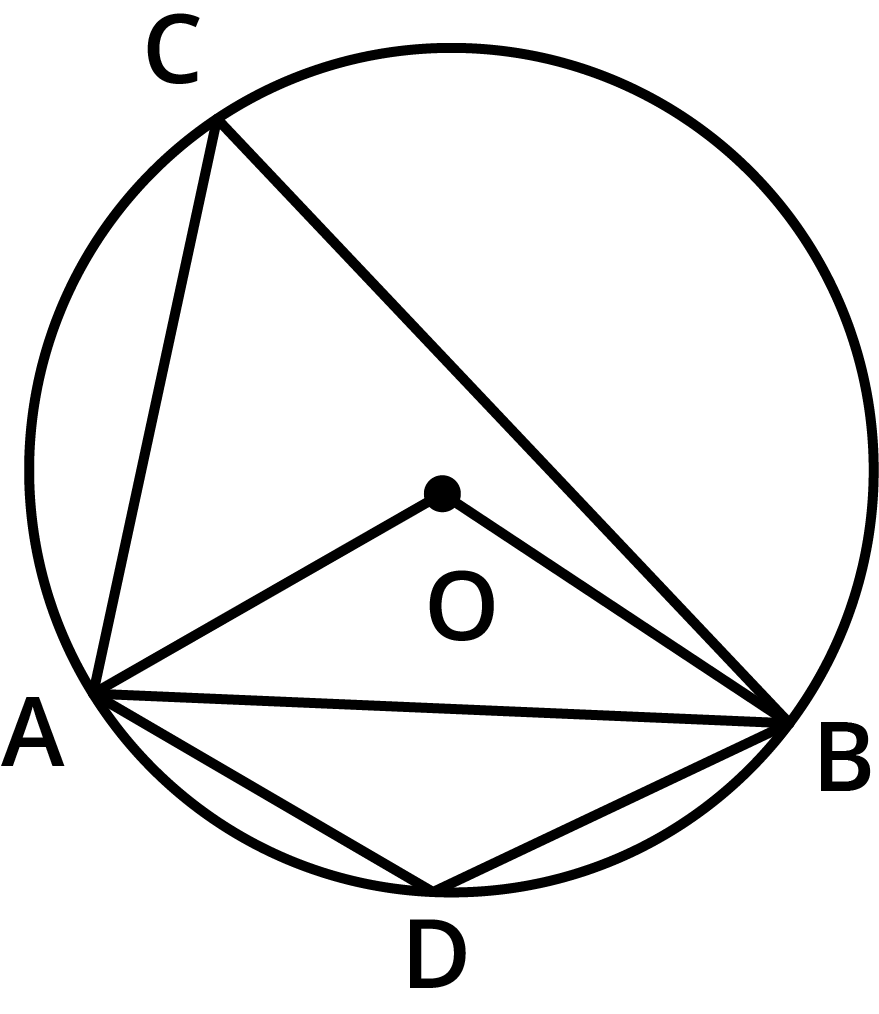
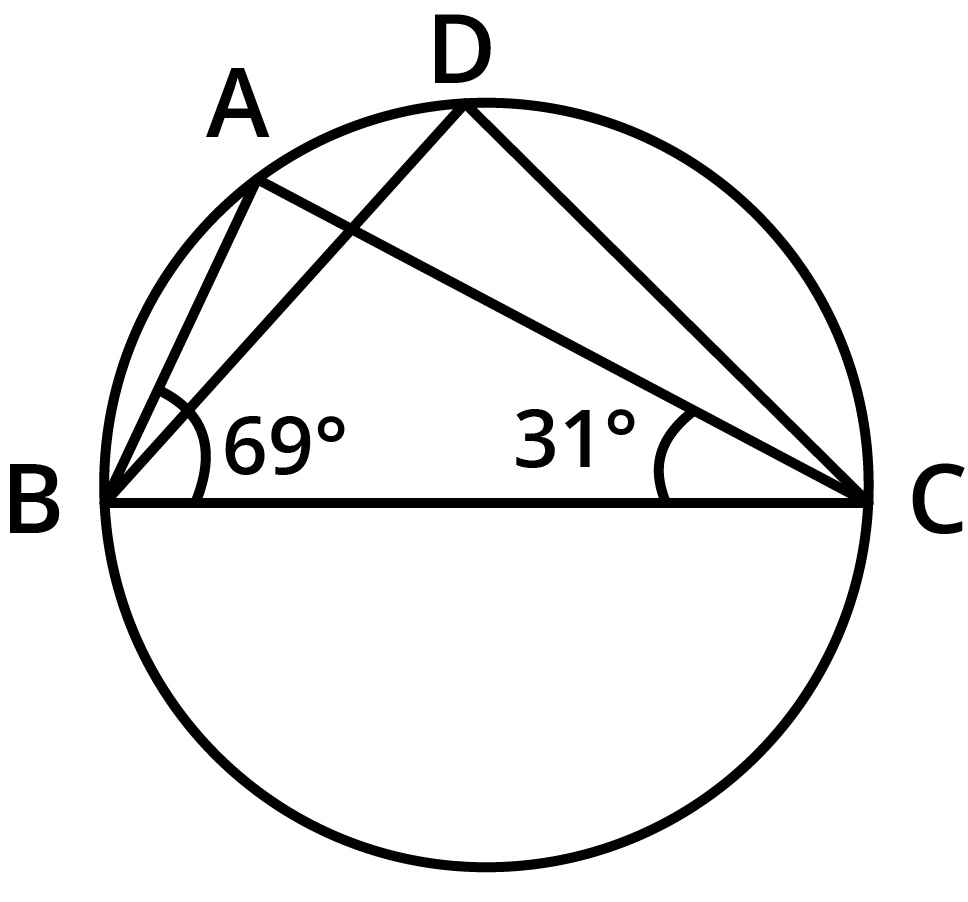
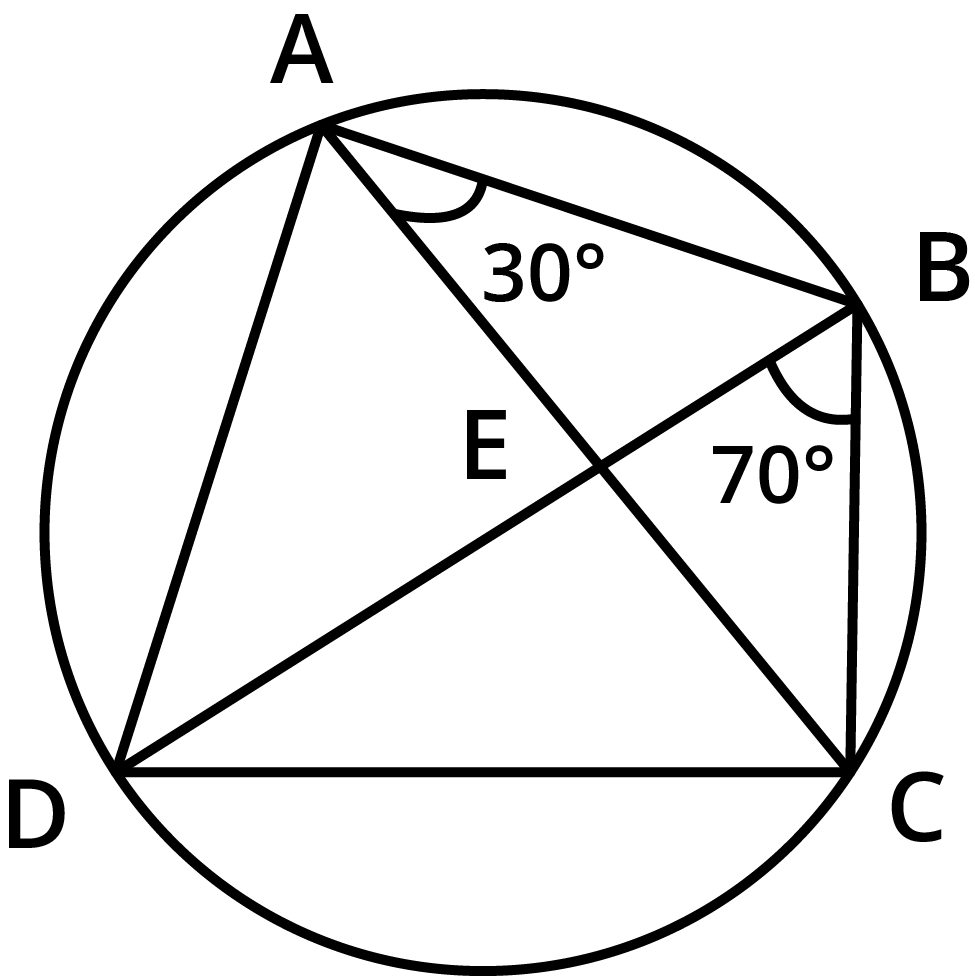
- Angles in the same segment of a circle are equal.
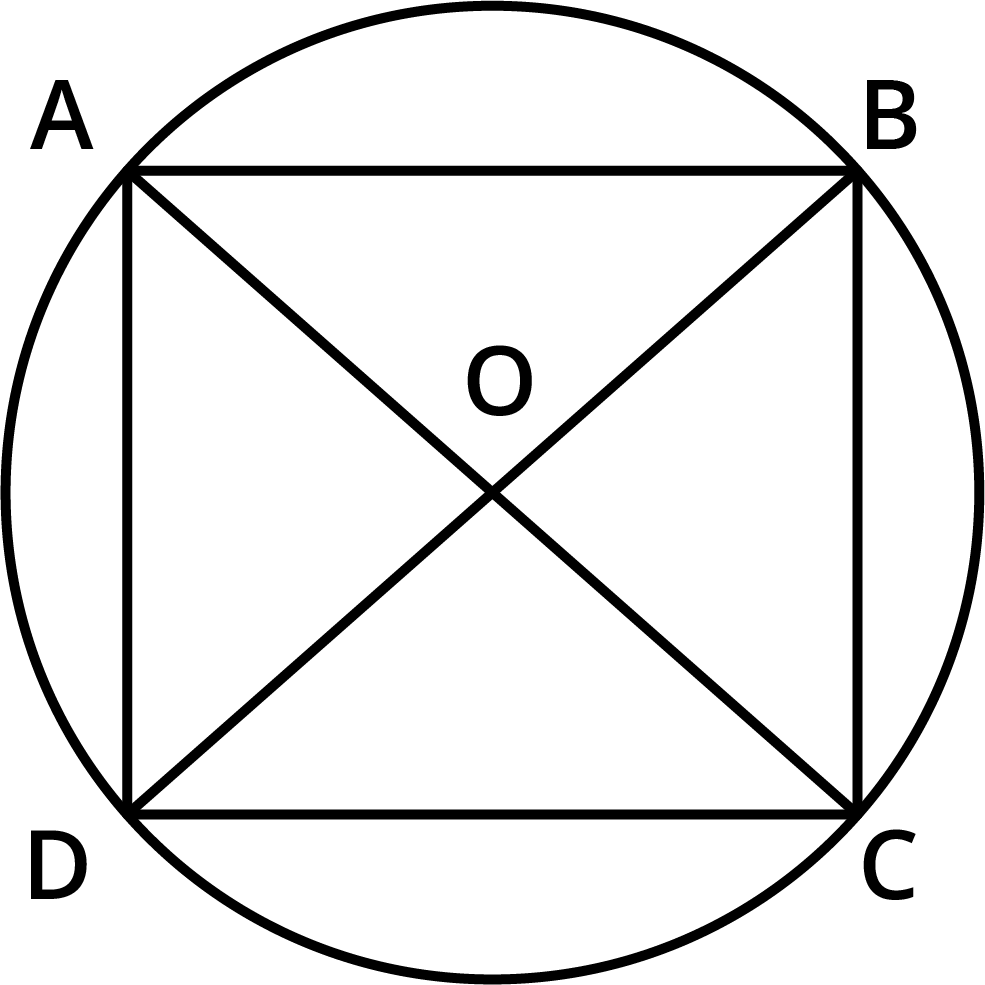
- The sum of either pair of opposite angles of a cyclic quadrilateral is 180°.
2. How do the NCERT Solutions demonstrate the step-by-step method for solving proof-based questions in Chapter 9?
The solutions follow a structured, CBSE-approved method for proofs, ensuring every step is justified:
- Given: Clearly stating all the information provided in the question.
- To Prove: Defining the specific objective that needs to be proven.
- Construction: Outlining any additional lines or points drawn to facilitate the proof.
- Proof: Providing a logical, sequential argument using established theorems and axioms to reach the final conclusion.
3. Why is drawing an accurate diagram considered a critical first step when solving problems from the Circles chapter?
Drawing an accurate diagram is a foundational step in geometry for several reasons. For Chapter 9, it helps you:
- Visualise the Problem: A clear diagram translates the text of the problem into a visual format, making it easier to understand the relationships between points, lines, chords, and arcs.
- Identify Applicable Theorems: By looking at the diagram, you can often spot potential geometric relationships, such as angles in the same segment or properties of a cyclic quadrilateral, which hints at the correct theorem to use.
- Plan the Solution: It aids in planning necessary constructions and the logical flow of the proof. An incorrect diagram can lead to flawed assumptions and a wrong solution.
4. How are the properties of a cyclic quadrilateral used to find unknown angles in the NCERT Solutions for this chapter?
The primary property of a cyclic quadrilateral used in the solutions is that the sum of opposite angles is 180°. To solve for an unknown angle, the step-by-step method is:
- Identify the quadrilateral inscribed within the circle.
- Ensure all four vertices of the quadrilateral lie on the circumference.
- Set up an equation where the sum of one pair of opposite angles equals 180°.
- If one angle is known, you can calculate its opposite angle by subtracting it from 180°.
- This property is frequently used in combination with other circle theorems to solve complex problems.
5. What is a common mistake to avoid when applying the theorem 'angle at the centre is double the angle at the circumference'?
A common mistake is failing to identify the correct arc that subtends both angles. The theorem only holds true when both the central angle and the angle on the circumference are subtended by the same arc. Students sometimes mistakenly relate an angle subtended by a major arc with an angle subtended by the corresponding minor arc. The NCERT solutions for Class 9 Maths Chapter 9 consistently clarify which arc is being considered to prevent this confusion.
6. How do the NCERT Solutions for Class 9 Maths Chapter 9 help master the concepts for the 2025-26 session?
The NCERT Solutions for the 2025-26 session help by providing detailed, step-by-step answers that align with the latest CBSE curriculum and marking scheme. They don't just provide the final answer but explain the 'how' and 'why' behind each step. By following these solutions, students can understand the correct method of applying theorems, learn how to structure their proofs, and identify common problem areas.
7. How can a student verify their answer for a proof in Chapter 9, Circles?
While a formal proof cannot be verified like a numerical answer, you can build confidence in your solution by using these methods:
- Logical Consistency Check: Reread your proof step-by-step. Does each statement logically follow from the previous one? Is every claim you made supported by a valid geometric theorem or axiom?
- Checking for Contradictions: Assume your final statement is false and see if it leads to a contradiction with the 'Given' information or a known theorem. If it does, your original proof is likely correct.
- Cross-referencing with Solved Examples: Compare your method with similar solved problems in the NCERT textbook or solutions to ensure your approach is sound.
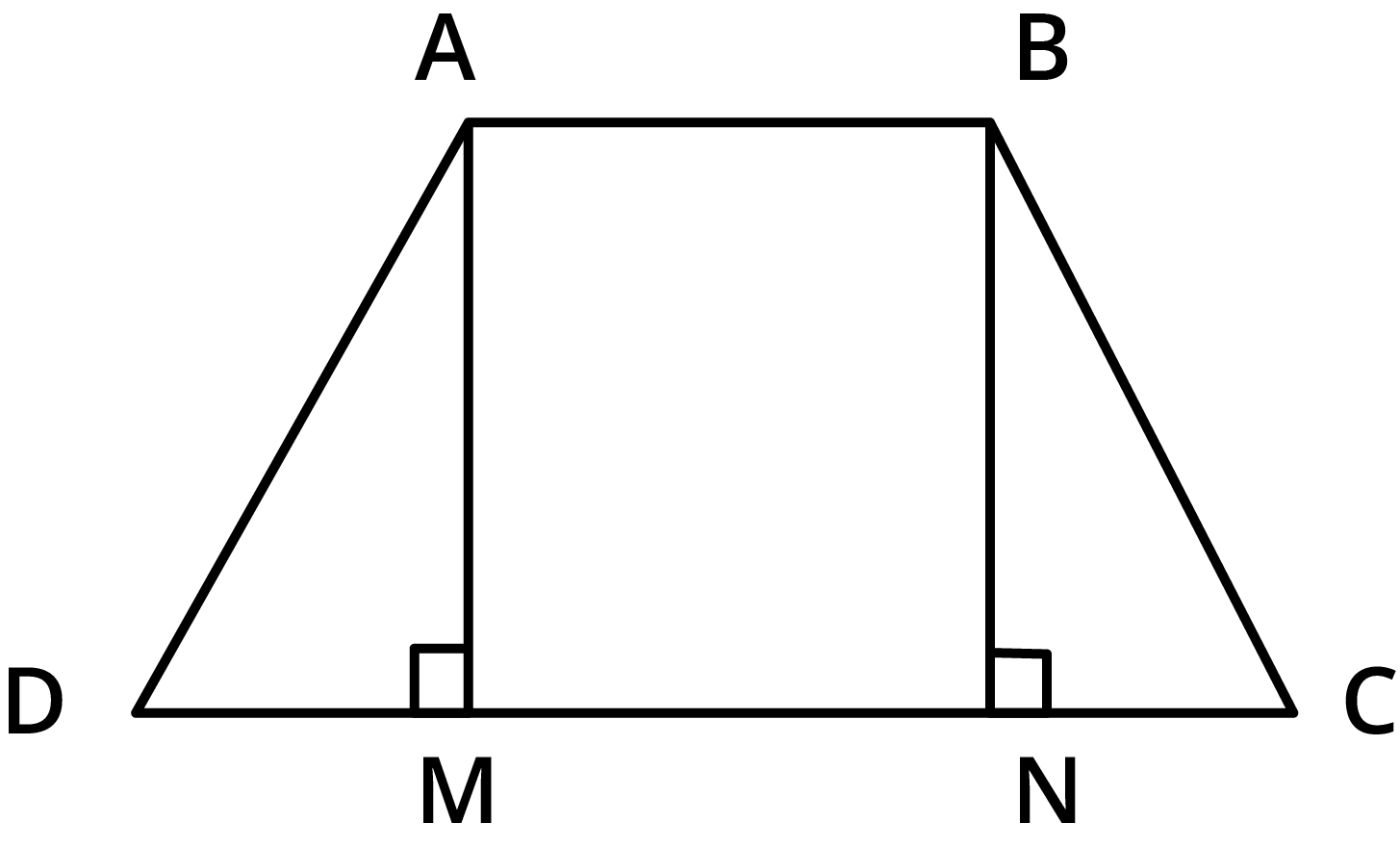
8. What is the correct approach to solve a problem that involves proving two chords or two circles are congruent?
To prove the congruence of chords or circles, the NCERT solutions for Chapter 9 typically use the following standard approach:
- Identify the Triangles: The most common method is to construct triangles that involve the chords or radii in question. For example, connect the endpoints of the chords to the centre of the circle.
- Use Congruence Rules: Apply triangle congruence rules like SSS (Side-Side-Side), SAS (Side-Angle-Side), or RHS (Right-angle-Hypotenuse-Side) to prove the constructed triangles are congruent.
- Apply CPCTC: Once the triangles are proven congruent, use the principle of 'Corresponding Parts of Congruent Triangles are Congruent' (CPCTC) to state that the corresponding chords or angles are equal, thus proving the required condition.




















 Watch Video
Watch Video