NCERT Solutions for Class 9 Maths Chapter 1 Number System - Free PDF 2024-25
NCERT Solutions for Class 9 Maths Chapter 1 Number Systems
FAQs on NCERT Solutions for Class 9 Maths Chapter 1 Number Systems
1. What are NCERT Solutions for Class 9 Maths Chapter 1 Number Systems, and how should students use them?
NCERT Solutions for Class 9 Maths Chapter 1 are detailed, step-by-step answers for every exercise question in the chapter Number Systems. Students should use these solutions to:
- Check their approach and understanding after attempting each question
- Learn CBSE-approved methods and formats of answering
- Clarify doubts in rational and irrational numbers, decimal expansions, and laws of exponents
- Strengthen concepts before exams and while doing homework, ensuring full syllabus coverage as per CBSE 2025–26
2. Which topics are most important in NCERT Solutions for Class 9 Maths Chapter 1 for scoring well in exams?
Key topics to focus on in Class 9 Maths Chapter 1 NCERT Solutions include:
- Classification of numbers: natural, whole, integers, rational, irrational, real
- Decimal expansions and distinguishing between terminating, non-terminating recurring, and non-recurring decimals
- Representation of real numbers on the number line
- Operations (addition, subtraction, multiplication, division) on real numbers
- Laws of exponents for real numbers
3. How do NCERT Solutions for Class 9 Maths Chapter 1 help in understanding rational and irrational numbers?
NCERT Solutions provide examples and stepwise justifications to help distinguish between rational and irrational numbers. These solutions:
- Show how every rational number can be represented as p/q, where q ≠ 0
- Offer criteria and examples for identifying irrational numbers (like √2, π)
- Explain common misconceptions (e.g., not all square roots are irrational; √4 = 2 is rational)
- Use conversion between decimal and fractional forms to deepen conceptual clarity
4. What are the common mistakes students must avoid when solving questions in Number Systems NCERT Solutions?
Common errors include:
- Confusing rational and irrational numbers, especially when converting decimals
- Incorrectly classifying numbers with non-terminating recurring decimals as irrational
- Forgetting to rationalize denominators as per CBSE method
- Not expressing answers in simplified or required p/q form
- Applying exponent rules incorrectly, especially with fractional and negative exponents
5. Why is rationalizing the denominator important in NCERT Solutions for Class 9 Maths Chapter 1?
Rationalizing the denominator simplifies expressions and aligns with standard CBSE presentation requirements. It ensures:
- The denominator has no irrational numbers, making further calculations and comparisons easier
- Marks are not lost due to step omissions, especially in board exams
- Clear understanding of using conjugates and exponent rules
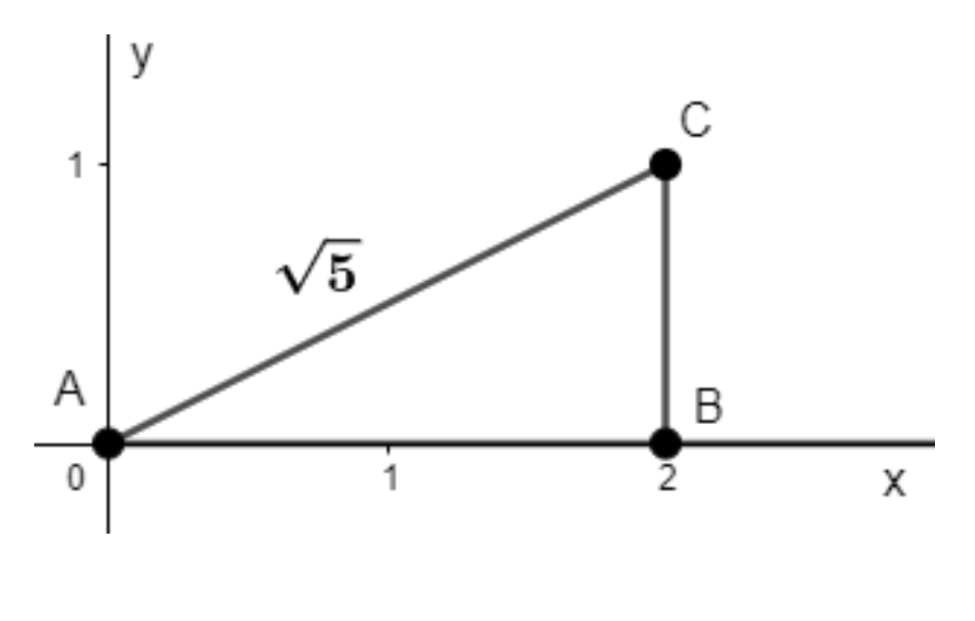
6. How can students represent $√{5}$ or other surds accurately on the number line as per CBSE methods?
To represent $\sqrt{5}$ on the number line:
- Draw a 2-unit line segment (AB)
- At B, erect a perpendicular of 1 unit (BC)
- Join AC; by Pythagoras, AC = $\sqrt{2^2 + 1^2} = \sqrt{5}$
- With A as center and radius AC, mark the point on the number line—this is the location of $\sqrt{5}$
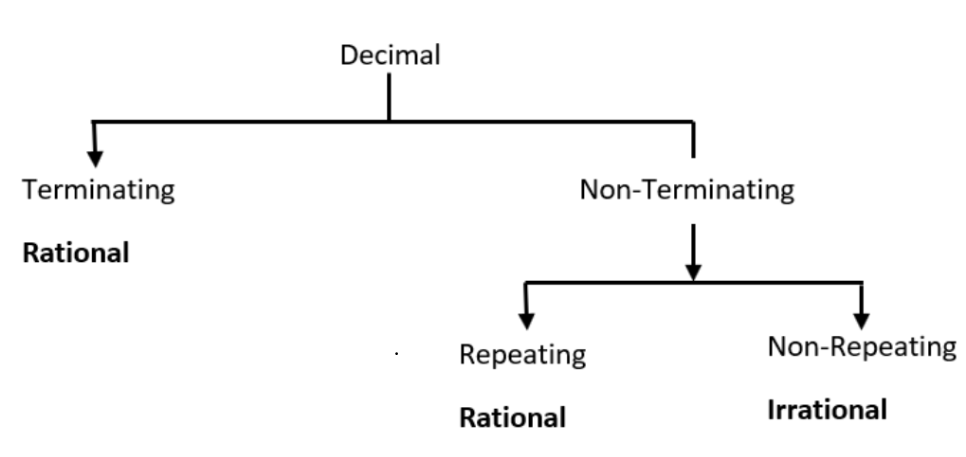
7. What strategy should students follow to identify terminating and non-terminating decimals using NCERT Solutions for Number Systems?
To determine decimal types:
- Express the number as p/q in lowest terms
- If the prime factors of q (denominator) are only 2 or 5 (or both), the decimal is terminating
- If q contains any other prime factors, the decimal is non-terminating recurring
- NCERT Solutions provide worked examples for both cases
8. How are exponents for real numbers handled in Class 9 Maths Chapter 1 NCERT Solutions?
The laws of exponents for real numbers are:
- $a^m × a^n = a^{m+n}$
- $(a^m)^n = a^{mn}$
- $a^0 = 1$ (a ≠ 0)
- $a^{-n} = 1/a^n$
- NCERT solutions explain roots as fractional exponents: $a^{1/n} = \sqrt[n]{a}$
9. How do NCERT Solutions clarify the difference between rational and irrational numbers for Class 9 Number Systems?
NCERT Solutions:
- Show rational numbers can always be written as p/q and have terminating or recurring decimals
- Explain irrational numbers cannot be written as p/q and have non-terminating, non-recurring decimals
- Provide clarity with concrete examples: $\frac{2}{3}$ (rational), $\sqrt{3}$ (irrational)
- Highlight that every real number is either rational or irrational (completeness property)
10. Why is it necessary to practice every question in the NCERT Solutions for Class 9 Maths Chapter 1?
Practicing all questions ensures students:
- Cover full range of CBSE exam question types
- Enhance problem-solving and reasoning skills
- Avoid missing out on less obvious, but examinable, concepts (like number representation or operation properties)
- Build confidence and accuracy before final exams
11. What if two different decimal numbers are very close, like 1 and 0.999..., are they considered equal according to NCERT Solutions?
NCERT Solutions explain that $0.999...$ is mathematically equal to 1 because their difference is zero. This is a key concept in understanding decimal representations and completeness of real numbers. Accepting this equivalence helps avoid errors in higher mathematics and aligns with CBSE standards.
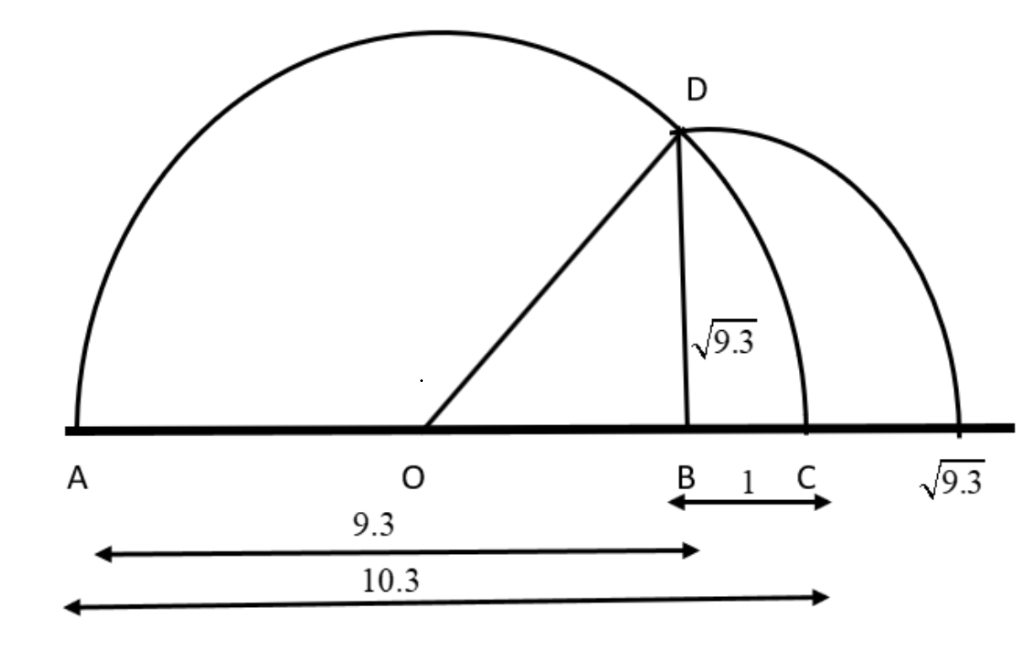
12. How are irrational numbers between two rationals found, as per NCERT Solutions for Number Systems?
To find irrational numbers between two given rationals (say $\frac{5}{7}$ and $\frac{9}{11}$):
- Convert both to decimal form
- Choose a non-repeating, non-terminating decimal between their values (e.g., 0.720202...)
- Alternatively, select a known irrational (like $\sqrt{2}$) and adjust to fit the interval, if possible
13. Can every point on the number line be written as the square root of a natural number, as per Class 9 NCERT guidelines?
No, not every point on the number line represents a square root of a natural number. While every real number corresponds to a unique point on the number line, only specific values correspond to exact square roots of naturals. NCERT clarifies this to correct misconceptions about surds and real numbers.
14. What are the official CBSE-recommended methods for simplifying expressions involving exponents and surds in Number Systems?
CBSE/NCERT recommends:
- Use laws of exponents to combine or simplify terms ($a^{m}a^{n} = a^{m+n}$)
- Express roots as fractional exponents ($\sqrt[n]{a} = a^{1/n}$)
- Rationalize denominators containing surds (e.g., multiply by conjugate if denominator has $\sqrt{a} + \sqrt{b}$)
- Always write the final answer in simplest form, as required by NCERT marking scheme














 Watch Video
Watch Video