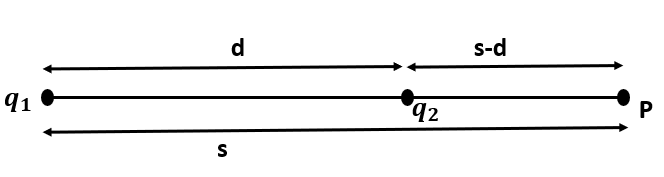
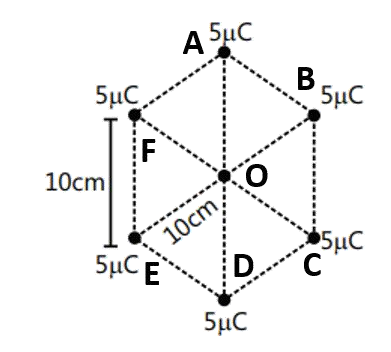
Class 12 Physics Chapter 2 Questions and Answers for Better Understanding



FAQs on NCERT Solutions for Class 12 Physics Chapter 2 Electrostatic Potential And Capacitance 2025-26
1. What are the main concepts covered in the NCERT Solutions for Class 12 Physics Chapter 2 Electrostatic Potential and Capacitance?
The NCERT Solutions for Class 12 Physics Chapter 2 focus on key concepts such as electrostatic potential, potential difference, capacitance, equipotential surfaces, types and combinations of capacitors (series and parallel), energy stored in a capacitor, and practical applications of capacitors. Fundamental formulas and theoretical derivations, as specified in the CBSE 2025–26 syllabus, are systematically explained to give students a strong foundation for exams and further studies.
2. How are stepwise solutions structured in NCERT Solutions for Class 12 Physics Chapter 2 according to CBSE guidelines?
The stepwise solutions follow the CBSE marking scheme:
- Each answer begins with the given data and clearly states what is required.
- Relevant formulas from the chapter are explicitly written and applied.
- Calculations are performed step by step with all units shown.
- The final answer is boxed or highlighted with correct units.
3. Why is understanding dielectric constant important in Electrostatic Potential and Capacitance NCERT Solutions?
Dielectric constant (K) determines how much the capacitance of a capacitor increases when a dielectric material is inserted. Understanding this helps students:
- Apply formulas for capacitance with and without dielectrics.
- Solve numerical questions involving changes in medium and plate separation.
- Explain why certain materials are used inside capacitors in electronics.
4. How do NCERT Solutions for Class 12 Physics Chapter 2 assist with solving capacitor combination problems?
The solutions provide systematic methods to solve problems involving capacitors in series and parallel:
- Formulas for equivalent capacitance in different arrangements are derived and used.
- Detailed steps for finding charge, voltage, and energy distribution across each capacitor are included.
- Common CBSE board question patterns, such as changing connections after charging or adding dielectrics, are addressed to prepare students for all possible scenarios.
5. What is the significance of equipotential surfaces in Class 12 Physics Chapter 2?
Equipotential surfaces are surfaces where electric potential remains constant. Their significance includes:
- Helping visualize the relationship between electric field and potential.
- Understanding conceptual and numerical problems about movement of charges, work done, and field direction.
- Exploration of equipotential properties is a commonly assessed conceptual topic in board exams.
6. What are some frequently asked application-based questions from Electrostatic Potential and Capacitance for board exams?
Application-based questions often involve:
- Calculating stored energy in capacitors before and after changes (such as connecting or disconnecting batteries or introducing dielectrics).
- Analyzing the effect of plate separation and dielectric material on capacitance.
- Comparing behavior and outcomes for series vs parallel combinations.
- Describing real-life uses of capacitors in electronic circuits.
7. How does the NCERT Solutions for Class 12 Physics Chapter 2 address potential errors and misconceptions?
Solutions highlight and correct common misconceptions, such as:
- The electric field inside a conductor is always zero (not just for spherical shells).
- Potential is constant inside a conductor, including cavities with no charge.
- Energy is always lost when a charged capacitor is connected to an uncharged one due to redistribution of charge.
- Capacitance depends only on geometry and dielectric, not on charge or potential directly.
8. What mathematical approach should students follow to solve numerical questions in NCERT Solutions for Class 12 Physics Chapter 2?
Students should:
- Start by noting all given values with correct units.
- Select and write relevant formulas explicitly.
- Substitute values step by step, ensuring unit consistency.
- Show all steps in calculations to earn full CBSE marks.
- Write the final answer clearly with appropriate units.
9. What is electrostatic potential, as defined in NCERT Solutions for Class 12 Physics Chapter 2?
Electrostatic potential (V) at a point is the work done by an external force in bringing a unit positive charge from infinity to that point, without acceleration, in an electric field. Its SI unit is volt (V), where 1 volt = 1 joule per coulomb. This basic definition is central to several numerical and conceptual board questions.
10. How is potential difference measured according to Class 12 Physics Chapter 2 NCERT Solutions?
Potential difference between two points is measured using a voltmeter, which must be connected in parallel with the two points in a circuit. Understanding this experimental process is important for both theoretical and practical exam questions.
11. What key formulas are essential from NCERT Solutions for Class 12 Physics Chapter 2?
Some essential formulas include:
- Electric potential energy: ΔU = W
- Capacitance: C = q/V
- Energy stored: E = (1/2)CV2 or (1/2)QV
- Series combination: 1/C = 1/C1 + 1/C2 + ...
- Parallel combination: C = C1 + C2 + ...
- Parallel plate capacitor: C = ε0A/d (with dielectric: C = Kε0A/d)
12. What is the change in electrostatic energy when a charged capacitor is connected to an identical uncharged capacitor, as per Class 12 Physics Chapter 2 Solutions?
The total electrostatic energy decreases due to redistribution of charge. The lost energy is dissipated as heat or radiation:
- Initial energy (Ei) = (1/2)CV2
- After connection, equivalent capacitance halves and energy (Ef) decreases by half
- Energy lost = Ei - Ef = half the initial energy
13. According to NCERT Solutions, what happens if a dielectric is inserted in a charged capacitor while the battery is connected versus when it is disconnected?
- With battery connected: Capacitance increases, charge on plates increases, voltage remains constant, total energy stored increases.
- With battery disconnected: Capacitance increases, charge on plates remains the same, voltage decreases, energy stored decreases.
14. Why is it important to study the combination of capacitors for the CBSE board exam?
Combination of capacitors covers:
- Key CBSE problem types on equivalent capacitance, charge, and voltage calculations.
- Understanding real-world circuits that use multiple capacitors for specific functions.
- Series and parallel combinations often feature in multi-step numerical and HOTS questions.
15. How can a student best use the NCERT Solutions for Class 12 Physics Chapter 2 to prepare for competitive exams like NEET or JEE?
Students should:
- Understand and practice derivations and numerical problems in depth.
- Master all key formulas and be able to apply them to multiple scenarios.
- Practice higher-order questions that combine concepts (e.g., fields, potential, and capacitance together).
- Review conceptual pitfalls and ensure clarity on why each formula applies in a scenario.