Electrostatic Potential and Capacitance Important Questions for CBSE Class 12 Physics Chapter 2

Very Short Answer Question (1 Mark Questions)

1. Why does the electric field inside a dielectric decrease when it is placed in an external electric field?

Ans: The electric field that is present inside a dielectric decreases when it is placed in an external electric field because of polarisation as it creates an internal electric field which is opposite to the external electric field inside a dielectric due to which the net electric field gets reduced.

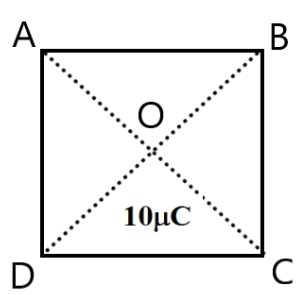
2. What is the work done in moving a $2\mu C$ point change from corner A to corner B of a square ABCD when a $10\mu C$ charge exists at the centre of the square?

Ans: Point A & B are at the same distance from point O.

Hence,

\[{{V}_{A}}={{V}_{B}}\]

$\Rightarrow \text{ Work done }=\text{0}$

3. Force of attraction between two point electric charges placed at a distance \[d\] in a medium is \[F\]. What distance apart should these be kept in the same medium, so that force between them becomes\[\frac{F}{3}\]?

Ans: If two point charges are \[{{q}_{1}}\] and \[{{q}_{2}}\] separated by distance \[d\], it can be expressed as:

\[F=\frac{K{{q}_{1}}{{q}_{2}}}{{{d}^{2}}}\]

Suppose if force becomes \[\frac{F}{3}\] let the distance be \[x\]

\[\frac{F}{3}=\frac{K{{q}_{1}}{{q}_{2}}}{{{x}^{2}}}\]

\[\Rightarrow \frac{K{{q}_{1}}{{q}_{2}}}{3{{d}^{2}}}=\frac{K{{q}_{1}}{{q}_{2}}}{{{x}^{2}}}\]

\[\Rightarrow {{x}^{2}}=3{{d}^{2}}\]

\[\Rightarrow x=\sqrt{3}d\]

4. The distance of the field point on the equatorial plane of a small electric dipole is halved. By what factors will the electric field due to the dipole changes?

Ans: The formula \[E\propto \frac{1}{{{r}^{3}}}\] gives the relation between electric field and distance. 

\[\therefore E\propto \frac{1}{{{\left( \frac{r}{2} \right)}^{3}}}\Rightarrow E\propto \frac{8}{{{r}^{3}}}\]

Therefore, the electric field becomes eight times larger.

5. The Plates of a charged capacitor are connected by a voltmeter. If the plates of the capacitor are moved further apart, what will be the effect on the reading of the voltmeter?

Ans: The relation between capacitance, area, distance and dielectric constant is \[C=\frac{A{{\in }_{0}}}{d}\Rightarrow C\propto \frac{1}{d}\]

Hence, if distance increases, capacitance decreases.

Since \[V=\frac{Q}{C}\] and charge on the capacitor is constant.

Hence reading of the voltmeter increases.

6. What happens to the capacitance of a capacitor when a dielectric slab is placed between its plates?

Ans: The introduction of dielectric in a capacitor will reduce the effective charge on plate and therefore will increase the capacitance.

Short Answer Questions (2 Marks Questions)

1. Show mathematically that the potential at a point on the equatorial line of an electric dipole is Zero?

Ans:  Electric potential at point on the equatorial line of an electric dipole can be expressed mathematically as:

\[V={{V}_{PA}}+{{V}_{PB}}\]

\[\Rightarrow V=\frac{K\left( -q \right)}{r}+\frac{K\left( +q \right)}{r}\]

\[\Rightarrow V=0\]

2. A parallel plate capacitor with air between the plates has a capacitance of \[8pF\]\[\left( 1pF={{10}^{-12}}F \right)\]. What will be the capacitance if the distance between the plates is reduced by half and the space between them is filled with a substance of dielectric constant \[6\]?

Ans: For air, capacitance can be expressed as, \[{{C}_{0}}=\frac{A{{\in }_{0}}}{d}\]

\[{{C}_{0}}=8\times pF=8\times {{10}^{-12}}F\]

Now \[{d}'=\frac{d}{2}\] and \[K=6\]

\[\Rightarrow {C}'=\frac{A{{C}_{0}}}{{{d}'}}\times 2\times K\]

\[\Rightarrow {C}'=8\times {{10}^{-12}}\times 2\times 6\]

\[\Rightarrow {C}'=96\times {{10}^{-12}}pF\]

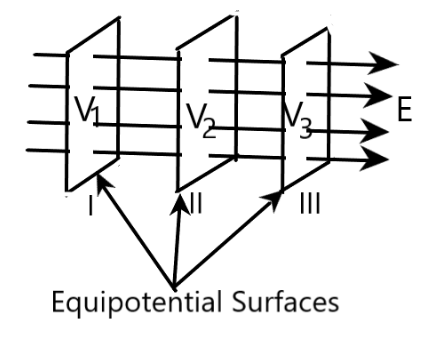
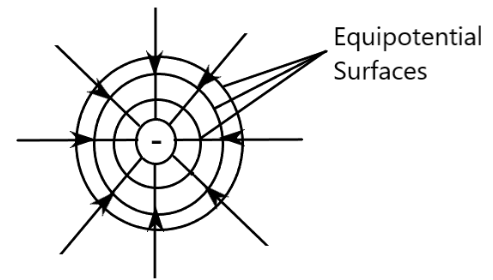
3. Draw one equipotential surfaces (1) Due to uniform electric field (2) For a point charge \[\left( q<0 \right)\]?

Ans: The diagrams are given as:

4. If the amount of electric flux entering and leaving a closed surface are \[{{\phi }_{1}}\] and \[{{\phi }_{2}}\] respectively. What is the electric charge inside the surface?

Ans: Net flux can be given as \[={{\phi }_{2}}-{{\phi }_{1}}\]

Since \[\phi =\frac{q}{{{\in }_{0}}}\]

\[\Rightarrow Q=\left( {{\phi }_{2}}-{{\phi }_{1}} \right){{\in }_{0}}\]

The electric charge inside the surface can be given as:

\[\Rightarrow Q=\phi {{\in }_{0}}\]

5. A stream of electrons travelling with speed \[v\,m/s\] at right angles to a uniform electric field E is deflected in a circular path of radius \[r\]. Prove that \[\frac{e}{m}=\frac{{{v}^{2}}}{rE}\]?

Ans: The path of the electron that is travelling with velocity \[v\,m/s\] at right angle of \[\overline{E}\] is of circular shape.

It requires a centripetal in nature, \[F=\frac{m{{v}^{2}}}{r}\]

It is provided by an electrostatic force \[F=eE\]

\[\Rightarrow eE=\frac{m{{v}^{2}}}{r}\]

\[\Rightarrow \frac{e}{m}=\frac{{{v}^{2}}}{rE}\]

6. The distance between the plates of a parallel plate capacitor is \[d\]. A metal plate of thickness \[\left( \frac{d}{2} \right)\] is placed between the plates. What will be the effect on the capacitance?

Ans: For air \[{{C}_{0}}=\frac{A{{\in }_{0}}}{d}\]

Thickness \[t=\frac{d}{2}\] only when \[k=\infty \]

\[{{C}_{0}}=\frac{A{{\in }_{0}}}{d}\]

\[{{C}_{metal}}=\frac{A{{\in }_{0}}}{\left( d-t \right)}\]

\[\Rightarrow {{C}_{metal}}=\frac{A{{\in }_{0}}}{\left( d-\frac{d}{2} \right)}\]

\[\Rightarrow {{C}_{metal}}=2A{{\in }_{0}}\]

\[\Rightarrow {{C}_{metal}}=2{{C}_{0}}\]

Hence, capacitance will double.

7. Two charges \[2\mu C\] and \[-2\mu C\] are placed at points A and B \[6cm\] apart.

(a) Identify an equipotential surface of the system.

Ans: The situation is represented in the adjoining figure.

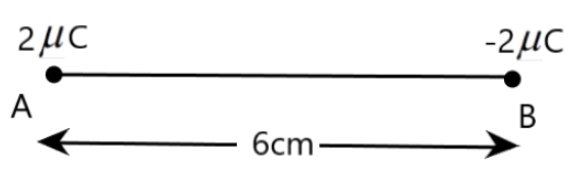
An equipotential surface is the plane on which the total potential is zero everywhere. This plane is normal to line AB. The plane is located at the mid-point of line AB because the magnitude of charges is the same.

(b) What is the direction of the electric field at every point on this surface?

Ans: The direction of the electric field at every point on this surface Is normal to the plane in the direction of AB.

8. In a Van de Graaff type generator a spherical metal shell is to be a 

\[15\times {{10}^{6}}V\]electrode. The dielectric strength of the gas surrounding the electrode is \[5\times {{10}^{7}}V{{m}^{-1}}\]. What is the minimum radius of the spherical shell required? (You will learn from this exercise why one cannot build an electrostatic generator using a very small shell which requires a small charge to acquire a high potential.)

Ans: Given that,

Potential difference is given as, \[V=15\times {{10}^{6}}V\]

Dielectric strength of the surrounding gas\[=5\times {{10}^{7}}V{{m}^{-1}}\]

Electric field intensity is given as, E = Dielectric strength = \[5\times {{10}^{7}}V{{m}^{-1}}\]

Minimum radius of the spherical shell required for the purpose is given by,

\[r=\frac{V}{E}\]

\[\Rightarrow r=\frac{15\times {{10}^{6}}}{5\times {{10}^{7}}}\]

\[\Rightarrow r=0.3m=30cm\]

Therefore, the minimum radius of the spherical shell required is \[30cm\].

9. A small sphere of radius \[{{r}_{1}}\] and charge \[{{q}_{1}}\] is enclosed by a spherical shell of radius \[{{r}_{2}}\] and charge \[{{q}_{2}}\]. Show that if \[{{q}_{1}}\] is positive, charge will necessarily flow from the sphere to the shell (when the two are connected by a wire) no matter what the charge \[{{q}_{2}}\] on the shell is.)

Ans: According to the statement of Gauss’s law, the electric field between a sphere and a shell is determined by the charge \[{{q}_{1}}\] on a small sphere. Therefore, the potential difference, \[V\], between the sphere and the shell is independent of charge \[{{q}_{2}}\]. For positive charge \[{{q}_{1}}\], potential difference \[V\]is always positive.

10. Describe schematically the equipotential surfaces corresponding to

(a) a constant electric field in the z-direction,

Ans: Equidistant planes which are parallel to the x-y plane are the equipotential surfaces.

(b) a field that uniformly increases in magnitude but remains in a constant (say, z) direction,

Ans: Planes parallel to the x-y plane are the equipotential surfaces with the exception that when the planes get closer, the field increases.

(c) a single positive charge at the origin, and

Ans: Concentric spheres centred at the origin are equipotential surfaces.

(d) a uniform grid consisting of long equally spaced parallel charged wires in a plane.

Ans: A periodically changing shape near the given grid is the equipotential surface. This shape gradually reaches the shape of planes parallel to the grid at a larger distance.

Short Answer Questions (3 Marks Questions)

1. Two dielectric slabs of dielectric constant \[{{K}_{1}}\] and \[{{K}_{2}}\] are filled in between the two plates, each of area \[A\], of the parallel plate capacitor as shown in the figure. Find the net capacitance of the capacitor? Area of each plate \[\frac{A}{2}\].

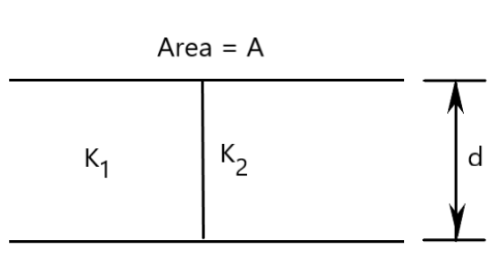
Ans: In the question, the two capacitors are in parallel

Net Capacitance, \[C={{C}_{1}}+{{C}_{2}}\] 

\[{{C}_{1}}=\frac{{{K}_{1}}{{\in }_{0}}\left( \frac{A}{2} \right)}{d}=\frac{{{K}_{1}}{{\in }_{0}}A}{2d}\]

\[{{C}_{2}}=\frac{{{K}_{2}}{{\in }_{0}}\left( \frac{A}{2} \right)}{d}=\frac{{{K}_{2}}{{\in }_{0}}A}{2d}\]

\[\Rightarrow C=\frac{{{K}_{1}}{{\in }_{0}}A}{2d}+\frac{{{K}_{2}}{{\in }_{0}}A}{2d}\]

\[\Rightarrow C=\frac{{{\in }_{0}}A}{2d}\left( {{K}_{1}}+{{K}_{2}} \right)\], which is the required capacitance.

2. Prove that the energy stored in a parallel plate capacitor is given by \[\frac{1}{2}C{{V}^{2}}\].

Ans: Let us suppose a capacitor is connected to a battery and it supplies a small amount of change \[dq\] at constant potential \[V\], then small amount of work done by the battery is given by

\[dw=Vdq\]

\[\Rightarrow dw=\frac{qc}{dq}\] …… (Since, \[q=CV\])

Total work done where the capacitor is fully changed to \[q\].

\[\int{dw=W}=\int_{0}^{q}{\frac{q}{c}dq}\]

\[\Rightarrow W=\int_{0}^{q}{qdq}\]

\[\Rightarrow W=\frac{{{q}^{2}}}{2C}=\frac{{{C}^{2}}{{V}^{2}}}{2C}\]

\[\Rightarrow W=\frac{1}{2}C{{V}^{2}}\]

This work done is stored in the capacitor in the form of electrostatic potential energy.

\[W=U=\frac{1}{2}C{{V}^{2}}\]

Hence proved.

3. State Gauss’s Theorem in electrostatics? Using this theorem, define an expression for the field intensity due to an infinite plane sheet of change of charge density \[\sigma C/{{m}^{2}}\].

Ans: Gauss’s Theorem has a statement that electric flux through a closed surface enclosing a charge \[q\] in vacuum is \[\frac{1}{{{\in }_{0}}}\] times the magnitude of the charge enclosed is \[\phi =\frac{q}{{{\in }_{0}}}\]

Let us consider a charge distributed over an infinite sheet of area S having surface change density\[\sigma C/{{m}^{2}}\]

To enclose the charge on sheet an imaginary Gaussian surface cylindrical in shape can be assumed and it is divided into three sections \[{{S}_{1}}\], \[{{S}_{2}}\] and \[{{S}_{3}}\].

According to Gauss’s theorem we can infer,

\[\phi =\frac{q}{{{\in }_{0}}}=\frac{\sigma S}{{{\in }_{0}}}\] …… (1)

We know that, \[\phi =\int{E\cdot ds}\]

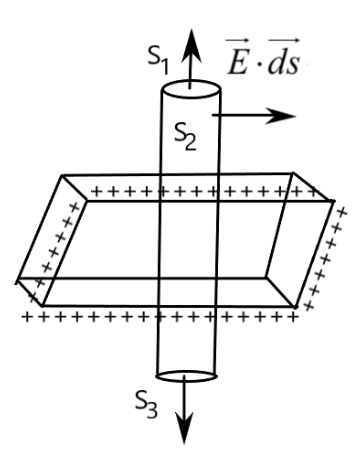
For the given surface \[\phi =\int\limits_{{{S}_{1}}}{\overrightarrow{E}\cdot \overrightarrow{ds}}+\int\limits_{{{S}_{2}}}{\overrightarrow{E}\cdot \overrightarrow{ds}}+\int\limits_{{{S}_{3}}}{\overrightarrow{E}\cdot \overrightarrow{ds}}\]

\[\Rightarrow \phi =\int\limits_{{{S}_{1}}}{E\cdot ds}\cos {{0}^{\circ }}+\int\limits_{{{S}_{3}}}{E\cdot ds}\cos {{0}^{\circ }}\] …… \[\left( \because \theta ={{90}^{\circ }}\,for\,{{S}_{2}}\,so\,\int\limits_{{{S}_{2}}}{\overrightarrow{E}\cdot \overrightarrow{ds}}=0 \right)\]

\[\Rightarrow \phi =E\int\limits_{{{S}_{1}}}{ds}+E\int\limits_{{{S}_{3}}}{ds}\]

\[\Rightarrow \phi =E\left[ \int_{0}^{S}{ds}+\int_{0}^{S}{ds} \right]\]

\[\Rightarrow \phi =E\cdot 2S\] ……(2)

From both equation (1) & (2)

\[E=\frac{\sigma }{2{{\in }_{0}}}\]

\[\Rightarrow E\cdot 2S=\frac{\sigma S}{{{\in }_{0}}}\], which is the required field intensity.

4. Derive an expression for the total work done in rotating an electric dipole through an angle \[\theta \] in a uniform electric field? \[E=1.5\times {{10}^{-8}}J\]

Ans: We know \[\tau =PE\sin \theta \]

If an electric dipole is rotated through an angle \[\theta \] against the torque, then small amount of work done is

\[dw=\tau d\theta =PE\sin \theta d\theta \]

For rotating through an angle \[\theta \] from \[{{90}^{\circ }}\]

\[W=\int_{{{90}^{\circ }}}^{\theta }{{}}PE\sin \theta \]

5. If \[{{C}_{1}}=3pF\] and \[{{C}_{2}}=2pF\], calculate the equivalent capacitance of the given network between A and B?

Ans: Since \[{{C}_{1}}\], \[{{C}_{2}}\]  and \[{{C}_{1}}\] are in series

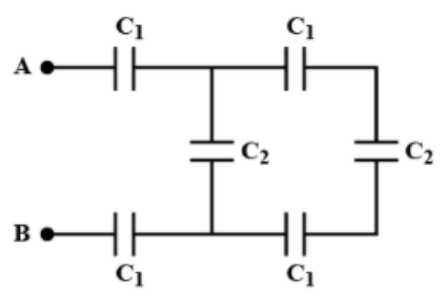
\[\frac{1}{C}=\frac{1}{{{C}_{1}}}+\frac{1}{{{C}_{2}}}+\frac{1}{{{C}_{3}}}\]

\[\Rightarrow \frac{1}{C}=\frac{1}{3}+\frac{1}{2}+\frac{1}{3}\]

\[\Rightarrow \frac{1}{C}=\frac{2+3+2}{6}\]

\[\Rightarrow C=\frac{6}{7}pF\]

\[{{C}_{2}}\] and C are in series

\[\Rightarrow {C}'=\frac{2}{1}+\frac{6}{7}=\frac{14+6}{7}=\frac{20}{7}pF\]

Here 

\[{{C}_{1}},{C}'\] and \[{{C}_{1}}\] are in series

\[\frac{1}{{{C}_{net}}}=\frac{1}{{{C}_{1}}}+\frac{1}{{{C}'}}+\frac{1}{{{C}_{1}}}\]

\[\Rightarrow \frac{1}{{{C}_{net}}}=\frac{1}{3}+\frac{7}{20}+\frac{1}{3}\]

\[\Rightarrow \frac{1}{{{C}_{net}}}=\frac{20+21+20}{60}=\frac{61}{60}\]

\[\Rightarrow \frac{1}{{{C}_{net}}}=\frac{61}{60}pF\Rightarrow {{C}_{net}}=\frac{60}{61}pF\], which is the net capacitance.

6. Prove that energy stored per unit volume in a capacitor is given by \[\frac{1}{2}{{\in }_{0}}{{E}^{2}}\], where E is the electric field of the capacitor.

Ans: We know capacitance of a parallel plate capacitor, \[C=\frac{A{{\in }_{0}}}{d}\], electric field in between the plates 

Energy stored per unit volume\[=\frac{Energy\,stored}{Volume}\]

Energy stored per unit volume\[=\frac{\frac{1}{2}\frac{{{q}^{2}}}{C}}{Ad}\] (Volume of the capacitor = Ad)

\[=\frac{\frac{1}{2}\times \frac{{{\left( \sigma A \right)}^{2}}}{\frac{A{{\in }_{0}}}{d}}}{Ad}=\frac{\frac{1}{2}\times {{E}^{2}}{{\in }^{2}}{{A}^{2}}d}{{{A}^{2}}{{\in }_{0}}d}\]

\[\Rightarrow \]Energy stored/volume\[=\frac{1}{2}{{\in }_{0}}{{E}^{2}}\]. 

Therefore, proved.

7. Keeping the voltage of the charging source constant. What would be the percentage change in the energy stored in a parallel plate capacitor if the separation between its plates were to be decreased by \[10%\]?

Ans: We have the relation, \[U=\frac{1}{2}C{{V}^{2}}\]

For parallel plate \[U=\frac{1}{2}\frac{A{{\in }_{0}}}{d}{{V}^{2}}\]

When \[{d}'=d-\frac{10}{100}\times d=0.9d\]

Then \[{U}'=\frac{1}{2}\frac{A{{\in }_{0}}}{0.9d}{{V}^{2}}\]

Change in energy\[={U}'-U=\frac{1}{2}\frac{A{{\in }_{0}}}{d}\left( \frac{1}{0.9}-1 \right)\]

\[={U}'-U=u\left( \frac{0.1}{0.9} \right)=\frac{U}{9}\]

\[%change=\frac{{U}'-U}{U}\times 100%=\frac{U}{9}\times \frac{1}{U}\times 100%=\frac{100}{9}%\]

\[\Rightarrow \% change=11.1%\]

8. Two identical plane metallic surfaces A and B are kept parallel to each other in air separated by a distance of \[1.0cm\] as shown in figure.

Surface A is given a positive potential of \[10V\] and the outer surface of B is earthed.

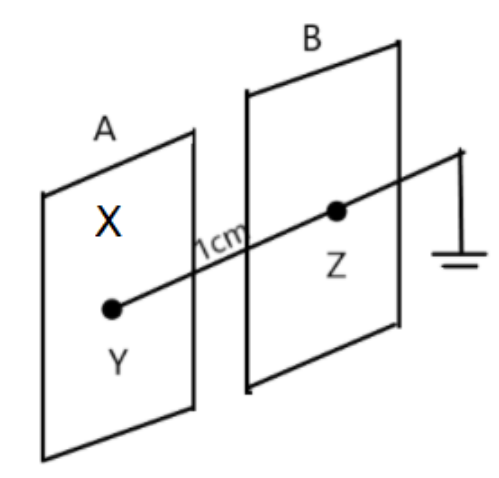
(a) What is the magnitude and direction of the uniform electric field between point Y and Z? What is the work done in moving a charge of \[20\mu C\] from point X to Y?

Ans:  Since \[E=\frac{dv}{dr}=\frac{10V}{1\times {{10}^{-2}}}=1000\frac{V}{M}\]

Since surface A is an equipotential surface i.e., \[\Delta V=0\]

$\therefore$ Work done in moving a charge of $20 \mu C$ from X to Y = Zero.

(b) Can we have non-zero electric potential in space, where electric field strength is zero?

Ans:  Since surface A is an equipotential surface i.e., \[\Delta V=0\]

$\therefore$ Work done from X to Y = Zero.

\[E=\frac{-dv}{dr}\] if \[E=0\]

\[\frac{dv}{dr}=0\Rightarrow dv=0\] or V=constant (non-zero)

So, we can have non-zero electric potential, where the electric field is zero.

9. A regular hexagon of side \[10cm\] has a charge \[5\mu C\] at each of its vertices. Calculate the potential at the centre of the hexagon.

Ans: The given figure shows six equal numbers of charges \[q\], at the vertices of a regular hexagon.

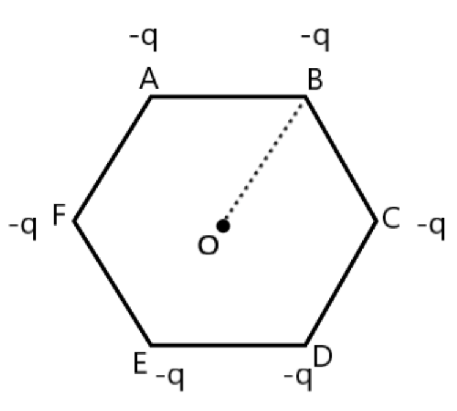
Where,

Charge, \[q=5\mu C=5\times {{10}^{-5}}C\]

Side of the hexagon, \[AB=BC=CD=DE=EF=FA=10cm\]

Distance of each vertex from center \[O\], \[d=10cm\]

Electric potential at point \[O\],

\[V=\frac{6\times q}{4\pi {{\in }_{0}}d}\]

Where,

\[{{\in }_{0}}\]permittivity of free space

\[\frac{1}{4\pi {{\in }_{0}}}=9\times {{10}^{9}}N{{C}^{-2}}{{m}^{-2}}\]

\[V=\frac{6\times 9\times {{10}^{9}}\times 5\times {{10}^{-5}}}{0.1}\]

\[\Rightarrow V=2.7\times {{10}^{6}}V\]

Therefore, the potential at the centre of the hexagon is \[2.7\times {{10}^{6}}V\].

10. A spherical conductor of radius \[12cm\] has a charge of \[1.6\times {{10}^{-7}}C\] distributed uniformly on its surface. What is the electric field? 

(a) Inside the sphere.

Ans: Radius of the spherical conductor is given as, \[r=12cm=0.12m\]

Charge is uniformly distributed over the conductor and can be given as, \[q=1.6\times {{10}^{-7}}C\]

Electric field inside a spherical conductor is zero. This is because if there is a field inside the conductor, then charges will move to neutralize it.

(b) Just outside the sphere 

Ans: Electric field E just outside the conductor is given by the relation,

\[E=\frac{q}{4\pi {{\in }_{0}}{{r}^{2}}}\]

Where,

\[{{\in }_{0}}=\]permittivity of free space

\[\frac{1}{4\pi {{\in }_{0}}}=9\times {{10}^{9}}N{{C}^{-2}}{{m}^{-2}}\]

\[\Rightarrow E=\frac{1.6\times {{10}^{-7}}\times 9\times {{10}^{-9}}}{{{\left( 0.12 \right)}^{2}}}\]

\[\Rightarrow E={{10}^{5}}N{{C}^{-1}}\]

Therefore, the electric field just outside the sphere \[={{10}^{5}}N{{C}^{-1}}\]

(c) At a point \[18cm\] from the centre of the sphere?

Distance of the point from the centre, \[d=18cm=0.18m\]

\[E=\frac{q}{4\pi {{\in }_{0}}{{d}^{2}}}\]

 \[\Rightarrow E=\frac{9\times {{10}^{9}}\times 1.6\times {{10}^{-7}}}{\left( 18\times {{10}^{-2}} \right)}\]

 \[\Rightarrow E=4.4\times {{10}^{4}}N/C\]

Therefore, the electric field at a point 18 cm from the centre of the sphere is \[4.4\times {{10}^{4}}N/C\].

11. Three capacitors each of capacitance \[9pF\] are connected in series.

(a) What is the total capacitance of the combination

Ans: Capacitance of each of the three capacitors, \[C=9pF\]

Equivalent capacitance \[{C}'\] of the combination of the capacitors is given by the relation,

\[\frac{1}{C}=\frac{1}{{{C}'}}+\frac{1}{{{C}'}}+\frac{1}{{{C}'}}\]

\[\Rightarrow \frac{1}{C}=\frac{1}{9}+\frac{1}{9}+\frac{1}{9}=\frac{3}{9}\]

\[\Rightarrow C=3\mu F\]

Therefore, the total capacitance of the combination is \[3\mu F\].

(b) What is the potential difference across each capacitor if the combination is connected to a \[120V\] supply?

Ans:  Supply voltage is given as, \[V=100V\]

Potential difference \[V\]  across each capacitor is equal to one-third of the supply voltage.

\[{V}'=\frac{V}{3}=\frac{120}{3}=40V\]

Therefore, the potential difference across each capacitor is \[40V\].

12. Three capacitors of each capacitance \[2pF\], \[3pF\] and \[4pF\]  are connected in parallel.

(a) What is the total capacitance of the combination?

Ans: Capacitance of the given capacitors are

\[{{C}_{1}}=2pF\]

\[{{C}_{2}}=3pF\]

\[{{C}_{3}}=4pF\]

For the parallel combination of the capacitors, equivalent capacitor \[{C}'\] is given by the algebraic sum,

\[{C}'=\left( 2+3+4 \right)pF\]

Therefore, the total capacitance of the combination is \[9pF\].

(b) Determine the charge on each capacitor if the combination is connected to a \[100V\] supply.

Ans:  Supply voltage, \[V=100V\]

The voltage through all the three capacitors is same as \[V=100V\] 

Charge on a capacitor of capacitance \[C\] and potential difference \[V\] is given by the relation,

\[q=CV\] …… (1)

For \[C=2pF\],

Charge\[=VC=100\times 2=200pC=2\times {{10}^{-10}}C\]

For \[C=3pF\], 

Charge\[=VC=100\times 3=300pC=3\times {{10}^{-10}}C\]

Now,

For \[C=4pF\], 

Charge\[=VC=100\times 4=400pC=4\times {{10}^{-10}}C\]

13. In a parallel plate capacitor with air between the plates, each plate has an area and the distance between the plates is \[3mm\]. Calculate the capacitance of the capacitor. If this capacitor is connected to a \[100V\] supply, what is the charge on each plate of the capacitor?

Ans: Area of each plate of the parallel plate capacitor, \[A=6\times {{10}^{-3}}{{m}^{2}}\]

Distance between the plates, \[d=3mm=3\times {{10}^{-3}}m\]

Supply voltage, \[V=100V\]

Capacitance \[C\] of a parallel plate capacitor is given by,

Where,

\[C=\frac{A{{\in }_{0}}}{d}\]

\[{{\in }_{0}}=\]permittivity of free space

\[\Rightarrow {{\in }_{0}}=8.854\times {{10}^{-12}}{{N}^{-1}}{{m}^{-2}}{{C}^{-2}}\]

\[\Rightarrow C=\frac{8.854\times {{10}^{-12}}\times 6\times {{10}^{-3}}}{3\times {{10}^{-3}}}\]

\[\Rightarrow C=17.71\times {{10}^{-12}}F\Rightarrow C=17.71pF\]

Potential \[V\] is related with the charge \[q\] and capacitance \[C\] as

\[V=\frac{q}{C}\Rightarrow q=VC\Rightarrow q=1.771\times {{10}^{-9}}C\]

\[\Rightarrow q=100\times 17.71\times {{10}^{-12}}C=17.71pF\]

Therefore, the capacitance of the capacitor is \[17.71pF\] and charge on each plate is \[1.771\times {{10}^{-9}}\].

14. Explain what would happen if in the capacitor given in Exercise 2.8, a \[3mm\] thick mica sheet (of dielectric constant \[=6\]) were inserted between the plates,

(a) While the voltage supply remained connected.

Ans: Dielectric constant of the mica sheet is given in the question as, \[k=6\]

Initial capacitance is provided as, \[C=1.771\times {{10}^{-11}}\]

New capacitance is given as, \[{C}'=kC=6\times 1.771\times {{10}^{-11}}=106pF\]

Supply voltage is given as, \[V=100V\]

New charge \[{q}'={C}'V=6\times 1.7717\times {{10}^{-9}}=1.06\times {{10}^{-8}}Cs\]

Potential across the plates remains \[100V\].

(b). After the supply was disconnected.

Ans: Dielectric constant is given in the question as, \[k=6\]

Initial capacitance, \[C=1.771\times {{10}^{-11}}F\]

New capacitance is given as \[{C}'=kC=6\times 1.771\times {{10}^{-11}}F=106pF\]

If supply voltage is removed, then there will be no effect on the amount of charge in the plates.

Charge \[=1.771\times {{10}^{-9}}C\]

Potential across the plates is given by,

\[V=\frac{q}{{{C}'}}\]

\[\Rightarrow V=\frac{1.771\times {{10}^{-9}}}{106\times {{10}^{-12}}}\]

\[\Rightarrow V=16.7V\]

15. A \[12pF\] capacitor is connected to a \[50V\] battery. How much electrostatic energy is stored in the capacitor?

Ans: Capacitor of the capacitance is given as, \[C=12pF=12\times {{10}^{-12}}F\]

Potential difference is provided as, \[V=50V\]

Electrostatic energy stored in the capacitor is given by the relation,

\[{{E}_{B}}=\frac{{{q}_{2}}}{4\pi {{\in }_{0}}{{\left( BZ \right)}^{2}}}\]

Now, 

\[\cos \theta =\frac{0.10}{0.18}=\frac{5}{9}=0.5556\]

\[\theta ={{\cos }^{-1}}0.5556={{56.25}^{\circ }}\]

\[\Rightarrow 2\theta ={{112.5}^{\circ }}\]

\[\Rightarrow \cos 2\theta =-0.38\]

Now, 

\[\overline{{{E}_{2}}}-\overline{{{E}_{1}}}=\frac{\sigma }{2{{\in }_{0}}}\hat{n}+\frac{\sigma }{2{{\in }_{0}}}\hat{n}=\frac{\sigma }{{{\in }_{0}}}\hat{n}\]

\[\Rightarrow E\left( 2\pi dL \right)=\frac{\lambda L}{{{\in }_{0}}}\]

\[\Rightarrow E\left( 2\pi dL \right)=\frac{{{q}_{1}}{{q}_{2}}}{4\pi {{\in }_{0}}{{d}_{1}}}-27.2eV\]

\[\Rightarrow E\left( 2\pi dL \right)=\frac{9\times {{10}^{9}}\times {{\left( 1.6\times {{10}^{-19}} \right)}^{2}}}{1.06\times {{10}^{-10}}}-27.2eV\]

\[\Rightarrow E\left( 2\pi dL \right)=21.73\times {{10}^{-10}}J-27.2eV\]

\[\Rightarrow E\left( 2\pi dL \right)=13.58eV-27.2eV\]

\[\Rightarrow E\left( 2\pi dL \right)=13.58eV\]

\[E=\frac{1}{2}C{{V}^{2}}\]

\[\Rightarrow E=\frac{1}{2}\times 12\times {{10}^{-12}}\times {{\left( 50 \right)}^{2}}\]

\[\Rightarrow E=1.5\times {{10}^{-8}}J\]

Therefore, the electrostatic energy stored in the capacitor is \[1.5\times {{10}^{-8}}J\].

16. A \[600pF\]capacitor is charged by a \[200V\] supply. It is then disconnected from the supply and is connected to another uncharged \[600pF\] capacitor. How much electrostatic energy is lost in the process?

Ans: Given that,

Capacitor of the capacitance, \[C=600pF\] 

Potential difference, \[V=200V\]

Electrostatic energy stored in the capacitor is given by,

\[E=\frac{1}{2}C{{V}^{2}}\]

\[\Rightarrow E=\frac{1}{2}\times \left( 600\times {{10}^{-12}} \right)\times {{\left( 200 \right)}^{2}}\]

\[\Rightarrow E=1.2\times {{10}^{-5}}J\]

If supply is disconnected from the capacitor and another capacitor of capacitance \[C=600pF\] is connected to it, then equivalent capacitance \[{C}'\] of the combination is given by,

\[\frac{1}{{{C}'}}=\frac{1}{C}+\frac{1}{C}\]

\[\Rightarrow \frac{1}{{{C}'}}=\frac{1}{600}+\frac{1}{600}=\frac{2}{600}=\frac{1}{300}\]

\[\Rightarrow {C}'=300pF\]

New electrostatic energy can be calculated as

\[{E}'=\frac{1}{2}{C}'\times {{V}^{2}}\]

\[{E}'=\frac{1}{2}\times 300\times {{\left( 200 \right)}^{2}}\]

\[{E}'=0.6\times {{10}^{-5}}J\]

Loss in electrostatic energy can be given as \[=E-{E}'\]

\[\Rightarrow E-{E}'=1.2\times {{10}^{-5}}-0.6\times {{10}^{-5}}\]

\[\Rightarrow E-{E}'=0.6\times {{10}^{-5}}\]

\[\Rightarrow E-{E}'=6\times {{10}^{-6}}J\]

Therefore, the electrostatic energy lost in the process is \[6\times {{10}^{-6}}J\].

17. A spherical conducting shell of inner radius \[{{r}_{1}}\] and outer radius \[{{r}_{2}}\] has a charge

(a) A charge \[q\] is placed at the centre of the shell. What is the surface charge density on the inner and outer surfaces of the shell?

Ans: Charge placed at the centre of a shell is \[+q\]. Hence a charge of magnitude \[-q\] will be induced to the inner surface of the shell. Therefore, total charge on the inner surface of the shell is \[-q\].

Surface charge density at the inner surface of the shell can be given by the relation,

\[{{\sigma }_{1}}=\frac{Total\,Charge}{Outer\,Surface\,Area}=\frac{-q}{4\pi {{r}_{1}}^{2}}\]

\[{{\sigma }_{2}}=\frac{Total\,Charge}{Outer\,Surface\,Area}=\frac{-q}{4\pi {{r}_{2}}^{2}}\]

A charge of \[+q\] is induced on the outer surface of the shell. A charge of magnitude \[Q\] is placed on the outer surface of the shell. Therefore, total charge on the outer surface of the shell is \[Q+q\]. Surface charge density at the outer surface of the shell.

(b) Is the electric field inside a cavity (with no charge) zero, even if the shell is not spherical, but any irregular shape? Explain.

Ans:  Yes, the electric field intensity which is inside a cavity is zero, even if the shell is not spherical and has any irregular shape. Now, take a closed loop such that a part of it is inside the cavity along a field line while the rest is inside the conductor. Net work done by the field in carrying a test charge over a closed loop will be zero due to the field inside the conductor being zero. Therefore, the electric field is zero, whatever the shape.

18. If one of the two electrons of a \[{{H}_{2}}\] molecule is removed, we get a hydrogen molecular ion \[{{H}_{2}}^{+}\]. In the ground state of an \[{{H}_{2}}^{+}\], the two protons are separated by roughly \[1.5{{A}^{\circ }}\], and the electron is roughly \[1{{A}^{\circ }}\] from each proton. Determine the potential energy of the system. Specify your choice of the zero of potential energy.

Ans: The system of two protons and one electron is represented in the given figure:

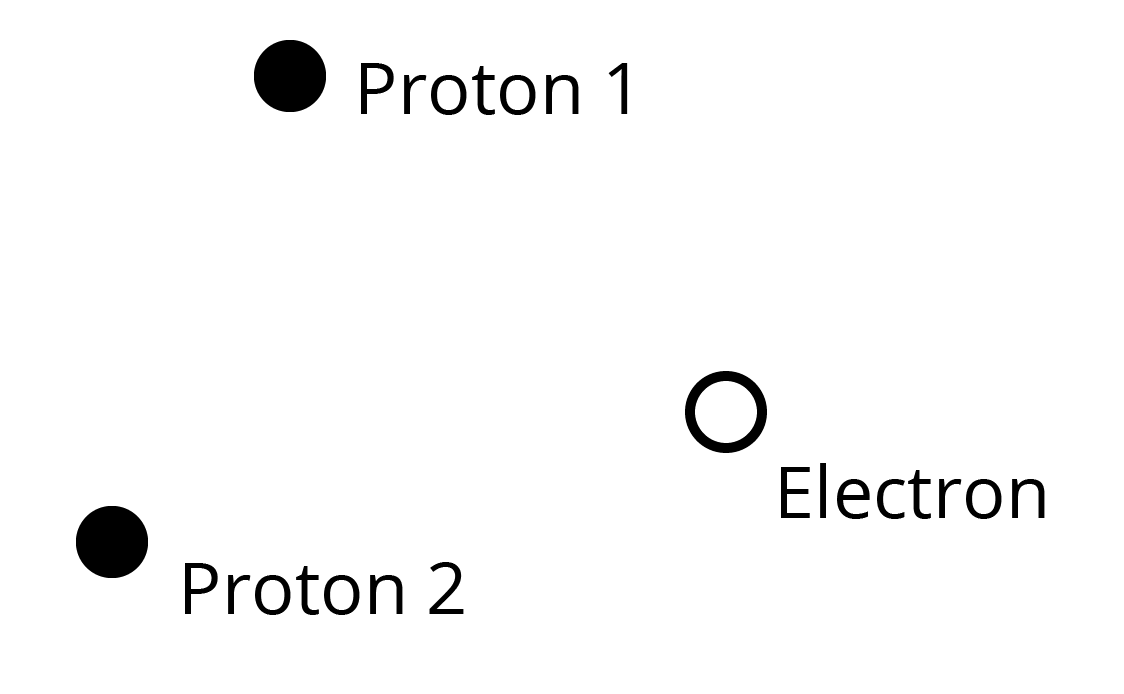
Charge on proton 1, \[{{q}_{1}}=1.6\times {{10}^{-19}}C\]

Charge on proton 2, \[{{q}_{2}}=1.6\times {{10}^{-19}}C\]

Charge on electron, \[{{q}_{3}}=-1.6\times {{10}^{-19}}C\]

Distance between protons 1 and 2, \[{{d}_{1}}=1.5\times {{10}^{-10}}m\]

Distance between proton 1 and electron, \[{{d}_{2}}=1\times {{10}^{-10}}m\]

Distance between protons 2 and electron, \[{{d}_{3}}=1\times {{10}^{-10}}m\]

The potential energy at infinity is zero.

Potential energy of the system,

\[V=\frac{{{q}_{1}}{{q}_{2}}}{4\pi {{\in }_{0}}{{d}_{1}}}+\frac{{{q}_{1}}{{q}_{3}}}{4\pi {{\in }_{0}}{{d}_{3}}}+\frac{{{q}_{3}}{{q}_{1}}}{4\pi {{\in }_{0}}{{d}_{2}}}\]

Substituting \[\frac{1}{4\pi {{\in }_{0}}d}=9\times {{10}^{9}}N{{m}^{2}}{{C}^{-2}}\]

\[V=\frac{9\times {{10}^{9}}\times {{10}^{-19}}}{{{10}^{-10}}}\left[ -{{\left( 16 \right)}^{2}}+\frac{{{\left( 1.6 \right)}^{2}}}{1.5}-{{16}^{2}} \right]\]

$\Rightarrow V=-30.7\times {{10}^{-19}}J $

$\Rightarrow V=-19.2eV$

Therefore, the potential energy of the system is \[-19.2eV\].

19. Two charged conducting spheres of radii \[a\] and \[b\] are connected to each other by a wire. What is the ratio of electric fields at the surfaces of the two spheres? Use the result obtained to explain why charge density on the sharp and pointed ends of a conductor is higher than on its flatter portions?

Ans: Let \[a\] be the radius of a sphere \[A\], \[{{Q}_{A}}\] be the charge on the sphere, and \[{{C}_{A}}\] be the capacitance of the sphere. Let \[b\] be the radius of a sphere \[B\], \[{{Q}_{B}}\] be the charge on the sphere, and \[{{C}_{B}}\] be the capacitance of the sphere. Since the two spheres are connected with a wire, their potential \[V\] will become equal.

Let \[{{E}_{A}}\] be the electric field of sphere \[A\] and \[{{E}_{B}}\] be the electric field of sphere \[B\]. Therefore, their ratio,

\[\frac{{{E}_{A}}}{{{E}_{B}}}=\frac{{{Q}_{A}}}{4\pi {{\in }_{0}}{{a}_{2}}}\times \frac{{{b}^{2}}4\pi {{\in }_{0}}}{{{Q}_{B}}}\]

\[\Rightarrow \frac{{{E}_{A}}}{{{E}_{B}}}=\frac{{{Q}_{A}}}{{{Q}_{B}}}\times \frac{{{b}^{2}}}{{{a}_{2}}}\]

However, 

\[\frac{{{Q}_{A}}}{{{Q}_{B}}}=\frac{{{C}_{A}}V}{{{C}_{B}}V}\]

And 

\[\frac{{{C}_{A}}}{{{C}_{B}}}=\frac{a}{b}\]

\[\frac{{{Q}_{A}}}{{{Q}_{B}}}=\frac{a}{b}\]

Putting the value of (2) in (1), we obtain

\[\frac{{{E}_{A}}}{{{E}_{B}}}=\frac{a}{b}\frac{{{b}^{2}}}{{{a}^{2}}}=\frac{b}{a}\]

Therefore, the ratio of the electric field at the surface is \[\frac{b}{a}\].

20. What is the area of the plates of a \[2F\] parallel plate capacitor, given that the separation between the plates is \[0.5cm\]? (You will realize from your answer why ordinary capacitors are in the range \[\mu F\] or less. However, electrolytic capacitors do have a much larger capacitance \[0.1F\] because of very minute separation between the electrolytic capacitors.)

Ans: Capacitance of a parallel capacitor, \[V=2F\]

Distance between the two plates, \[d=0.5cm=0.5\times {{10}^{-2}}m\]. Capacitance of a parallel plate capacitor is given by the relation,

Where,

\[{{\in }_{0}}=\]permittivity of free space\[=8.85\times {{10}^{-12}}{{C}^{2}}{{N}^{-1}}{{m}^{2}}\]

\[A=\frac{2\times 0.5\times {{10}^{-2}}}{8.85\times {{10}^{-12}}}\]

\[\Rightarrow A=1130k{{m}^{2}}\]

Hence, the area of the plates is too large. To avoid this situation, the capacitance is taken in the range of \[\mu F\].

21. A spherical capacitor consists of two concentric spherical conductors, held in position by suitable insulating supports (Fig. 2.36).

(Image will be uploaded soon)

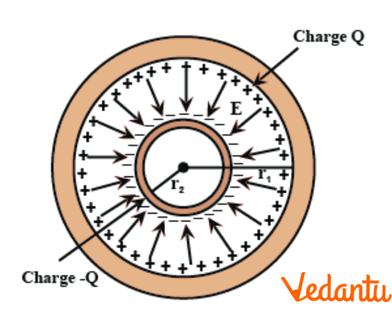
Show that the capacitance of a spherical capacitor is given by\[C=\frac{4\pi {{\in }_{0}}{{r}_{1}}{{r}_{2}}}{{{r}_{1}}-{{r}_{2}}}\] where \[{{r}_{1}}\] and \[{{r}_{2}}\] re the radii of outer and inner spheres, respectively.

Ans: Given that,

Radius of the outer shell is given in the question as\[={{r}_{1}}\]

Radius of the inner shell is given as\[={{r}_{2}}\]

The inner surface of the outer shell's charge can be given as \[+Q\].

\[V=\frac{Q}{4\pi {{\in }_{0}}{{r}_{2}}}-\frac{Q}{4\pi {{\in }_{0}}{{r}_{1}}}\]

The outer surface of the inner shell has induced charge \[-Q\]. Potential difference between the two shells is given by,

Where,

\[{{\in }_{0}}=\]permittivity of free space

\[V=\frac{Q}{4\pi {{\in }_{0}}}\left[ \frac{1}{{{r}_{2}}}-\frac{1}{{{r}_{1}}} \right]\]

\[\Rightarrow V=\frac{Q\left( {{r}_{1}}-{{r}_{2}} \right)}{4\pi {{\in }_{0}}{{r}_{1}}{{r}_{2}}}\]

Capacitance of the given system is given by,

\[C=\frac{Charge\,\left( Q \right)}{Potential\,Difference\,\left( V \right)}\]

\[\Rightarrow C=\frac{4\pi {{\in }_{0}}{{r}_{1}}{{r}_{2}}}{{{r}_{1}}-{{r}_{2}}}\]

Therefore, proved.

22. A cylindrical capacitor has two co-axial cylinders of length \[15cm\] and radii \[1.5cm\] and \[1.4cm\]. The outer cylinder is earthed and the inner cylinder is given a charge of \[3.5\mu C\]. Determine the capacitance of the system and the potential of the inner cylinder. Neglect end effects (i.e., bending of field lines at the ends).

Ans: Given that,

Length of a co-axial cylinder is given as, \[l=15cm=0.15m\]

Radius of the outer cylinder is given as, \[{{r}_{1}}=1.5cm=0.015m\]

Radius of the inner cylinder is given as, \[{{r}_{2}}=1.4cm=0.014m\]

Charge on the inner cylinder, \[q=3.5\mu C=3.5\times {{10}^{-6}}C\]

Capacitance of a co-axial cylinder of radii \[{{r}_{1}}\] and \[{{r}_{2}}\] is given by the relation,

\[C=\frac{2\pi {{\in }_{0}}l}{{{\log }_{2}}\left( \frac{{{r}_{1}}}{{{r}_{2}}} \right)}\]

Where,

\[{{\in }_{0}}=\]permittivity of free space\[=8.85\times {{10}^{-12}}{{N}^{-1}}{{m}^{-2}}{{C}^{2}}\]

\[C=\frac{2\pi \times 8.85\times {{10}^{-12}}\times 0.15}{2.3026{{\log }_{10}}\left( \frac{0.15}{0.14} \right)}\]

\[\Rightarrow C=\frac{2\pi \times 8.85\times {{10}^{-12}}\times 0.15}{2.3026\times 0.0299}=1.2\times {{10}^{-10}}F\]

Potential difference of the inner cylinder is given by,

\[V=\frac{Q}{C}\]

\[\Rightarrow V=\frac{3.5\times {{10}^{-6}}}{1.2\times {{10}^{-10}}}=2.92\times {{10}^{4}}V\]

23. A parallel plate capacitor is to be designed with a voltage rating \[1kV\], using a material of dielectric constant \[3\]and dielectric strength about \[{{10}^{7}}V{{m}^{-1}}\]. (Dielectric strength is the maximum electric field a material can tolerate without breakdown, i.e., without starting to conduct electricity through partial ionisation). For safety, we should like the field never to exceed, say \[10%\] of the dielectric strength. What minimum area of the plates is required to have a capacitance of \[50pF\]?

Ans: Given that,

Potential rating of a parallel plate capacitor, \[V=1kV=1000V\]

Dielectric constant of a material, \[{{\in }_{r}}=3\] Dielectric strength\[={{10}^{7}}V/m\]

For safety, the field intensity never exceeds 10%of the dielectric strength. Hence, electric field intensity, \[E=10%\] of \[{{10}^{7}}={{10}^{6}}V/m\]

Capacitance of the parallel plate capacitor, $C=50pF=50\times10^{-12}F$

Distance between the plates is given by,

\[d=\frac{V}{E}\]

\[\Rightarrow d=\frac{1000}{{{10}^{6}}}\]

\[\Rightarrow d={{10}^{-3}}m\]

Capacitance is given by the relation,

\[C=\frac{{{\in }_{0}}{{\in }_{1}}A}{d}\]

Where,

\[A=\]area of each plate

\[{{\in }_{0}}=\]permittivity of free space\[=8.85\times {{10}^{-12}}{{N}^{-1}}{{m}^{-2}}{{C}^{2}}\]

\[A=\frac{CD}{{{\in }_{0}}{{\in }_{1}}}\]

\[\Rightarrow A=\frac{50\times {{10}^{-12}}\times {{10}^{-3}}}{8.85\times {{10}^{-12}}\times 3}=19c{{m}^{2}}\]

Hence, the area of each plate is about \[19c{{m}^{2}}\].

Long Answer Questions (5 Mark Questions)

1.

(a) Define dielectric constant in terms of the capacitance of a capacitor. On what factor does the capacitance of a parallel plate capacitor with dielectric depend?

Ans: Dielectric constant can be expressed as the ratio of capacitance of a capacitor when the dielectric is filled in between the plates to the capacitance of a capacitor when there is vacuum in between the plates.

In \[K=\frac{{{C}_{m}}}{{{C}_{o}}}=\frac{\text{Capacitance of a capacitor when dielectric is in between the plates}}{\text{Capacitance of a capacitor with vacuum in between the plates}}\]

Capacitance of a parallel plate capacitor with dielectric depends on the following factors

\[{{C}_{m}}=\frac{KA{{\in }_{0}}}{d}\]

Area of the plates

Distance between the plates

Dielectric constant of the dielectric between the plates.

(b) Find the ratio of the potential differences that must be applied across the 

(i) Parallel

(ii) Series combination of two identical capacitors so that the energy stored in the two cases becomes the same.

Ans: Let the capacitance of each capacitor be \[C\]

\[{{C}_{p}}=\frac{C\times C}{C+C}=\frac{C}{2}\] …… (in series)

Let \[{{V}_{p}}\] and \[{{V}_{s}}\] be the values of potential difference

Thus \[{{U}_{p}}=\frac{1}{2}\times {{C}_{p}}\times {{V}_{p}}^{2}=\frac{1}{2}\times 2C\times {{V}_{p}}^{2}=C{{V}_{p}}^{2}\]

\[{{U}_{s}}=\frac{1}{2}\times {{C}_{s}}\times {{V}_{s}}^{2}=\frac{1}{2}\times \frac{C}{2}\times {{V}_{s}}^{2}=\frac{C{{V}_{s}}^{2}}{4}\]

But \[{{U}_{p}}={{U}_{s}}\] …… (given)

\[C{{V}_{p}}^{2}=\frac{C{{V}_{s}}^{2}}{4}\]

\[\Rightarrow \frac{{{V}_{p}}^{2}}{{{V}_{s}}^{2}}=\frac{1}{4}\]

\[\Rightarrow {{V}_{p}}:{{V}_{s}}=1:2\]

2. 

(a) An air-filled capacitor is given a charge of \[2\mu C\] raising its potential to \[200V\]. If on inserting a dielectric medium, its potential falls to \[50V\], what is the dielectric constant of the medium?

Ans: \[K=\frac{V}{{{V}'}}=\frac{200}{50}=4\] (where \[V=200V\] for air filled capacitor \[{V}'=50\] after insertion of a dielectric)

(b) A conducting slab of thickness \[t\] is introduced without touching between plates of a parallel plate capacitor separated by a distance d, \[t<d\]. Derive an expression for the capacitance of a capacitor?

Ans: For a parallel plate capacitor when air/vacuum is in between the plates \[{{C}_{0}}=\frac{A{{\in }_{0}}}{d}\]

Since the electric field inside a conducting stab is zero, hence the electric field exists only between the space \[\left( d-t \right)\Rightarrow V={{E}_{0}}\left( d-t \right)\]

Where \[{{E}_{0}}\] is the electric field between the plates.

And \[{{E}_{0}}=\frac{\sigma }{{{\in }_{0}}}=\frac{q}{A{{\in }_{0}}}\]

Where \[A\] is the area of each plate

\[\Rightarrow V=\frac{q}{A{{\in }_{0}}}\left( d-t \right)\]

Hence capacitor of a parallel plate capacitor

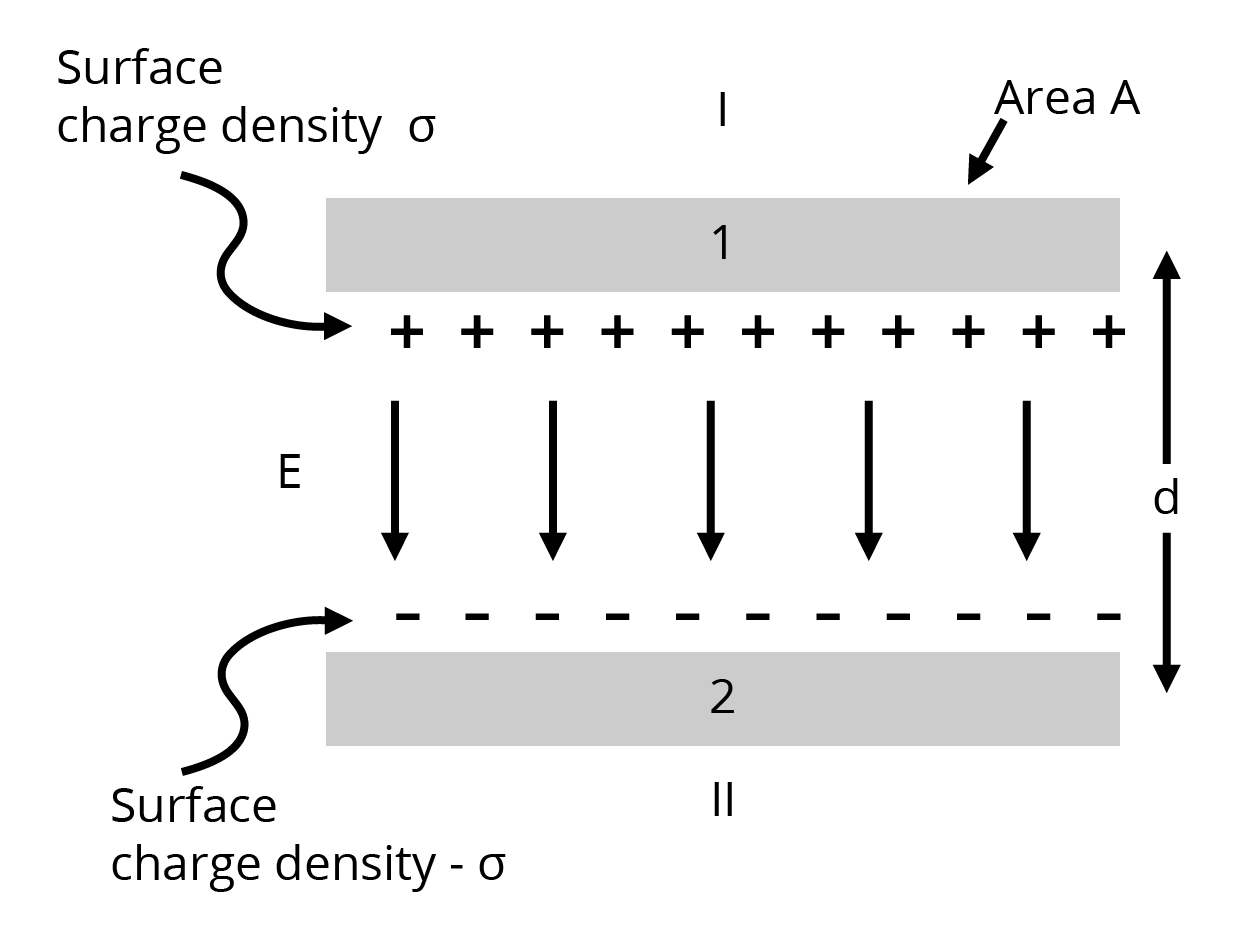
\[C=\frac{q}{V}=\frac{q}{q\left( d-t \right)}A{{\in }_{0}}\]

\[\Rightarrow C=\frac{A{{\in }_{0}}}{d-t}\]

\[\Rightarrow C=\frac{A{{\in }_{0}}}{d\left( 1-\frac{t}{d} \right)}\]

\[\Rightarrow C=\frac{{{C}_{0}}}{\left( 1-\frac{t}{d} \right)}\]

3. Figure (a) and (b) shows the field lines of a single positive and negative changes respectively

(a) Give the signs of the potential: \[{{V}_{P}}-{{V}_{Q}}\] and \[{{V}_{B}}-{{V}_{A}}\]

Ans: We know the relation as \[V\propto \frac{1}{r}\]

\[{{V}_{P}}>{{V}_{Q}}\Rightarrow {{V}_{P}}-{{V}_{Q}}\,=\,Positive\]

\[{{V}_{A}}<{{V}_{B}}\Rightarrow {{V}_{B}}-{{V}_{A}}\,=\,Positive\]

Because \[{{V}_{B}}\] is less negative than \[{{V}_{A}}\].

(b) Give the sign of the work done by the field in moving a small positive change from \[Q\] to \[P\].

Ans: In moving a positive change form \[Q\] to \[P\] work has to be done against the electric field so it is negative, and the sign is, hence, negative.

(c) Give the sign of the work done by the field in moving a small negative change from \[B\] to \[A\].

Ans:  In moving a negative change form \[B\] to \[A\] work is done along the same direction of the field so it is positive, and the sign is, hence, positive.

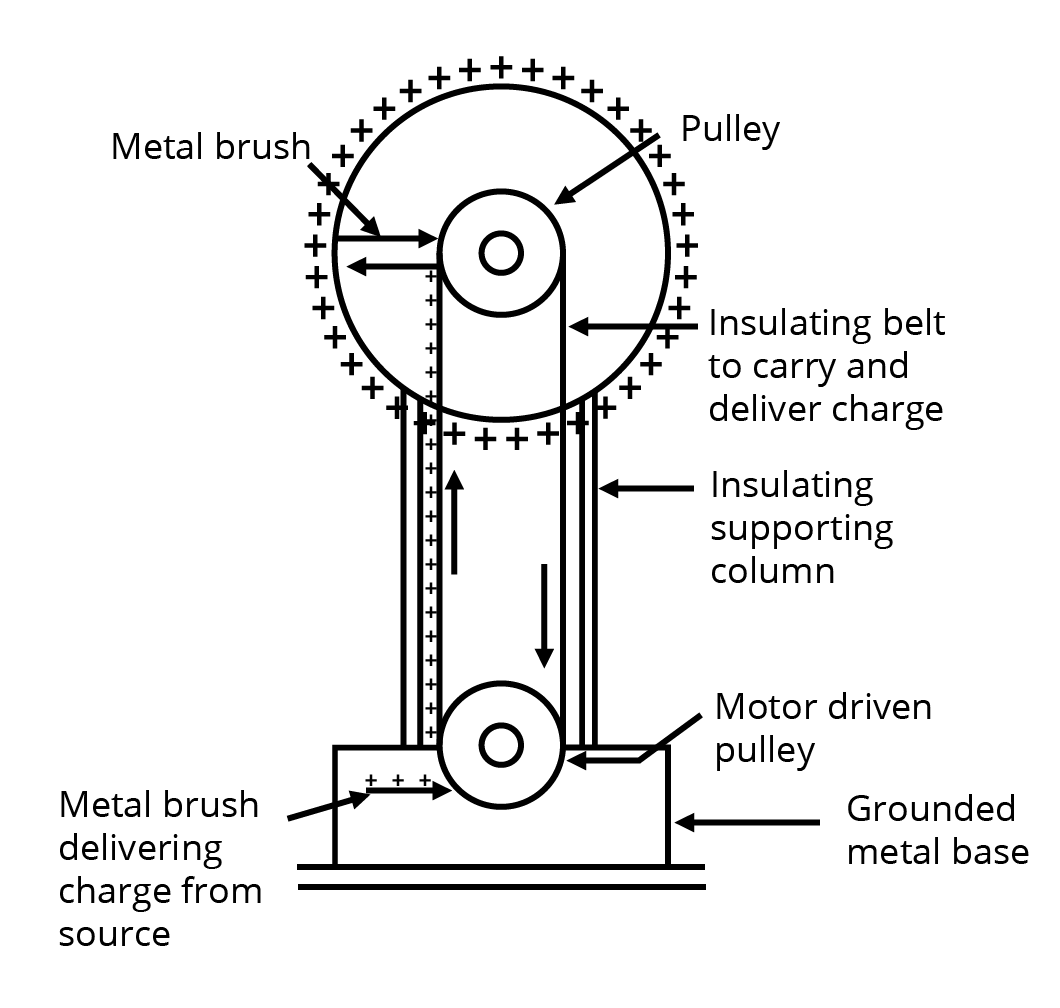
4. With the help of a labelled diagram, explain the principle, construction and working of a Van de Graff generator. Mention its applications.

Ans: Van de Graff generator can be expressed as a device which is capable of producing a high potential of the order of million volts.

Principle: 

The charge always resides on the outer surface of the hollow conductor.

The electric discharge in air or gas takes place readily at the pointed ends of the conductors.

Construction of Van de Graff Generator: 

It consists of a large hollow metallic sphere \[S\] mounted on two insulating columns A and B and an endless belt made up of rubber which is running over two pulleys \[{{P}_{1}}\] and \[{{P}_{2}}\] with the help of an electric motor. \[{{B}_{1}}\] and \[{{B}_{2}}\] are two sharp metallic brushes. The lower brush \[{{B}_{1}}\] is given a positive potential by high tension battery and is called a spray brush while the upper brush \[{{B}_{2}}\] connected to the inner part of the sphere \[S\].

Working: 

When brush \[{{B}_{1}}\] is given a higher positive potential then it produces ions, due to the action of sharp points. Thus, the positive ions so produced get sprayed on the belt due to repulsion between positive ions and the positive charge on brush \[{{B}_{1}}\]. Then it is carried upward by the moving belt. The pointed end of \[{{B}_{2}}\] just touches the belt collects the positive change and make it move to the outer surface of the sphere S. This process continues and the potential of the shell rises to several million volts.

Applications: 

Particles like protons, deuterons, \[\alpha \]-particles etc are accelerated to high speeds and energies.

5. Two charges \[5\times {{10}^{-8}}C\] and \[-3\times {{10}^{-8}}C\] are located \[16cm\] apart. At what point(s) on the line joining the two charges is the electric potential zero? Take the potential at infinity to be zero.

Ans: There are two charges which are given as,

\[{{q}_{1}}=5\times {{10}^{-8}}C\]

\[{{q}_{2}}=-3\times {{10}^{-8}}C\]

Distance between the two charges, \[d=16cm=0.16m\]

Consider a point \[P\] on the line joining the two charges, as shown in the given figure.

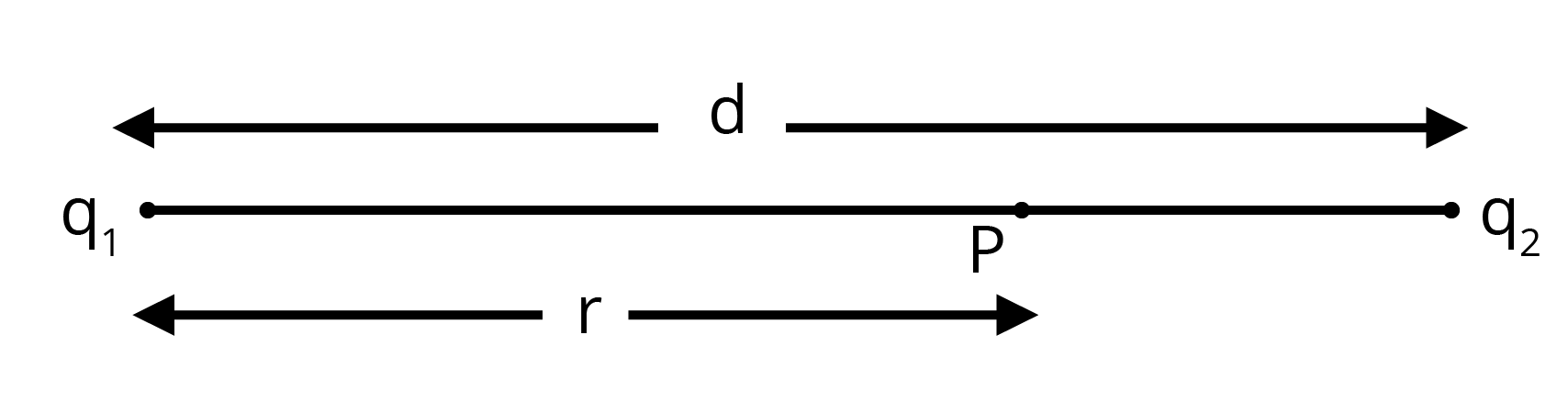
\[r=\] distance of point \[P\] from charge \[{{q}_{1}}\]

Let the electric potential \[V\] at point \[P\] be zero.

Potential at point \[P\] is the sum of potentials caused by charges \[{{q}_{1}}\] and \[{{q}_{2}}\] respectively.

\[V=\frac{{{q}_{1}}}{4\pi {{\in }_{0}}r}+\frac{{{q}_{2}}}{4\pi {{\in }_{0}}\left( d-r \right)}\] …… (1)

Where,

\[{{\in }_{0}}=\]permittivity of free space

For \[V=0\], equation (1) reduces to

\[\frac{{{q}_{1}}}{4\pi {{\in }_{0}}r}=-\frac{{{q}_{2}}}{4\pi {{\in }_{0}}\left( d-r \right)}\]

\[\Rightarrow \frac{{{q}_{1}}}{r}=-\frac{{{q}_{2}}}{\left( d-r \right)}\]

\[\Rightarrow \frac{5\times {{10}^{-8}}}{r}=\frac{\left( -3\times {{10}^{-8}} \right)}{\left( 0.16-r \right)}\]

\[\Rightarrow \frac{0.16}{r}=\frac{8}{5}\]

\[\Rightarrow r=0.1m=10cm\]

Therefore, the potential is zero at a distance of \[10cm\] from the positive charge between the charges.

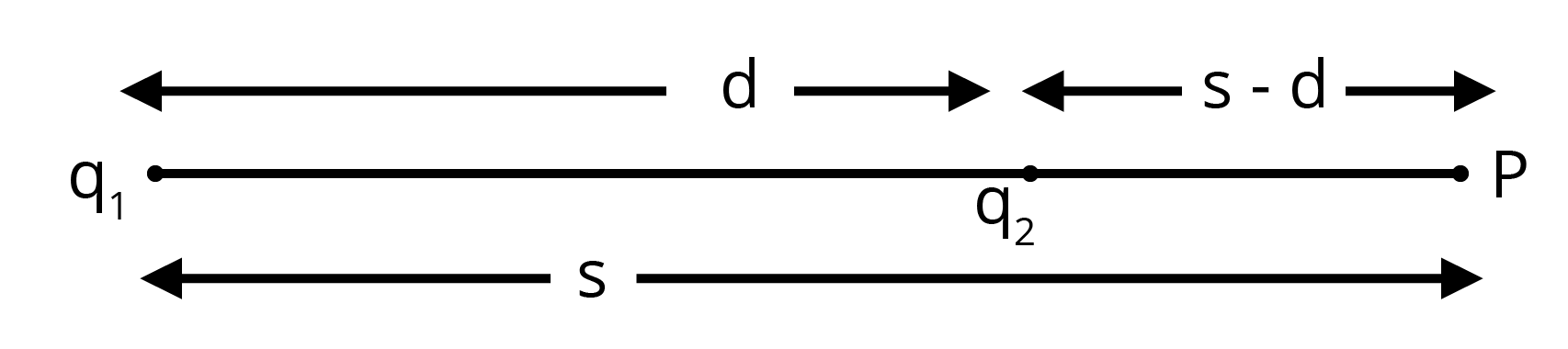
Suppose point \[P\] is outside the system of two charges where potential is zero, as shown in the given figure.

For this arrangement, potential is given

 \[V=\frac{{{q}_{1}}}{4\pi {{\in }_{0}}s}+\frac{{{q}_{2}}}{4\pi {{\in }_{0}}\left( s-d \right)}\]…… (2)

For \[V=0\], equation (2) reduces to

\[\frac{{{q}_{1}}}{4\pi {{\in }_{0}}s}=-\frac{{{q}_{2}}}{4\pi {{\in }_{0}}\left( s-d \right)}\]

\[\Rightarrow \frac{{{q}_{1}}}{s}=-\frac{{{q}_{2}}}{\left( s-d \right)}\]

\[\Rightarrow \frac{5\times {{10}^{-8}}}{s}=\frac{\left( -3\times {{10}^{-8}} \right)}{\left( s-0.16 \right)}\]

\[\Rightarrow 1-\frac{0.16}{s}=\frac{3}{5}\]

\[\Rightarrow \frac{0.16}{s}=\frac{2}{5}\]

\[\Rightarrow s=0.4m=40cm\]

Therefore, the potential is zero at a distance of \[40cm\] from the positive charge outside the system of charges.

6. A parallel plate capacitor with air between the plates has a capacitance of \[8pF\], \[\left( 1pF={{10}^{-12}}F \right)\]. What will be the capacitance if the distance between the plates is reduced by half, and the space between them is filled with a substance of dielectric constant \[6\]?

Ans: Capacitance between the parallel plates of the capacitor, \[C=8pF\]

Initially, the distance between the parallel plates was \[d\] and it was filled with air. Dielectric constant of air, \[k=1\]

Capacitance, \[C\] is given by the formula,

\[C=\frac{kA{{\in }_{0}}}{d}\]

\[\Rightarrow C=\frac{A{{\in }_{0}}}{d}\] ……(1)

Where,

\[A=\] Area of each plate

\[{{\in }_{0}}=\] Permittivity of free space

If distance between the plates is reduced to half, then the new distance can be given as, \[{{d}^{-TM}}=\frac{d}{2}\]. Dielectric constant of the substance filled in between the plates, \[{k}'=6\]. 

Therefore, capacitance of the capacitor becomes

\[{C}'=\frac{{k}'A{{\in }_{0}}}{d}=\frac{6A{{\in }_{0}}}{\frac{d}{2}}\] …… (2)

Taking the ratios of equation \[1\] and \[2\], we obtain

\[{C}'=2\times 6C\]

\[\Rightarrow {C}'=12C\]

\[\Rightarrow {C}'=12\times 8=96pF\]

Therefore, the capacitance between the plates is \[96pF\].

7. A charge of \[8mC\] is located at the origin. Calculate the work done in taking a small charge of \[-2\times {{10}^{-9}}C\] from a point \[P\left( 0,0,3 \right)cm\] to a point \[Q\left( 0,4,0 \right)cm\], via a point \[R\left( 0,6,9 \right)cm\].

Ans: Charge located at the origin is given as, \[q=8mC=8\times {{10}^{3}}C\].

Magnitude of a small charge, which is taken from a point \[P\] to point \[R\] to point \[Q\].

\[{{q}_{1}}=-2\times {{10}^{-9}}C\]

All the points are represented in the figure below.

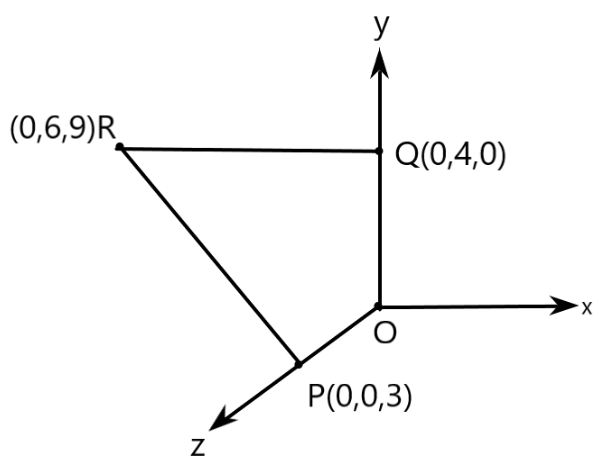
Point \[P\] is at a distance, \[{{d}_{1}}=3cm\] from the origin along z-axis. Point \[Q\] is at a distance, \[{{d}_{2}}=4cm\], from the origin along y-axis.

Potential at point \[P\]can be given as, \[{{V}_{1}}=\frac{q}{4\pi {{\in }_{0}}{{d}_{1}}}\]

Potential at point \[Q\], \[{{V}_{2}}=\frac{q}{4\pi {{\in }_{0}}{{d}_{2}}}\]

Work done \[W\] by the electrostatic force is independent of the path.

\[W={{q}_{1}}\left( {{V}_{2}}-{{V}_{1}} \right)\]

\[\Rightarrow W={{q}_{1}}\left[ \frac{q}{4\pi {{\in }_{0}}{{d}_{2}}}-\frac{q}{4\pi {{\in }_{0}}{{d}_{1}}} \right]\]

\[\Rightarrow W=\frac{{{q}_{1}}{{q}_{2}}}{4\pi {{\in }_{0}}}\left[ \frac{1}{{{d}_{2}}}-\frac{1}{{{d}_{1}}} \right]\] …… (1)

Where, 

\[\frac{1}{4\pi {{\in }_{0}}}=9\times {{10}^{9}}N{{m}^{2}}{{C}^{-2}}\]

\[\Rightarrow W=9\times {{10}^{9}}\times 8\times {{10}^{-3}}\times \left( -2\times {{10}^{-9}} \right)\left[ \frac{1}{0.04}-\frac{1}{0.03} \right]\]

\[\Rightarrow W=-144\times {{10}^{-3}}\times \left( \frac{-25}{3} \right)\]

\[\Rightarrow W=1.27J\]

Therefore, work done during the process is \[1.27J\].

8. A cube of side \[b\]has a charge \[q\] at each of its vertices. Determine the potential and electric field due to this charge array at the centre of the cube.

Ans: Length of the side of a cube is given as \[=b\]

Charge at each of its vertices\[=q\]

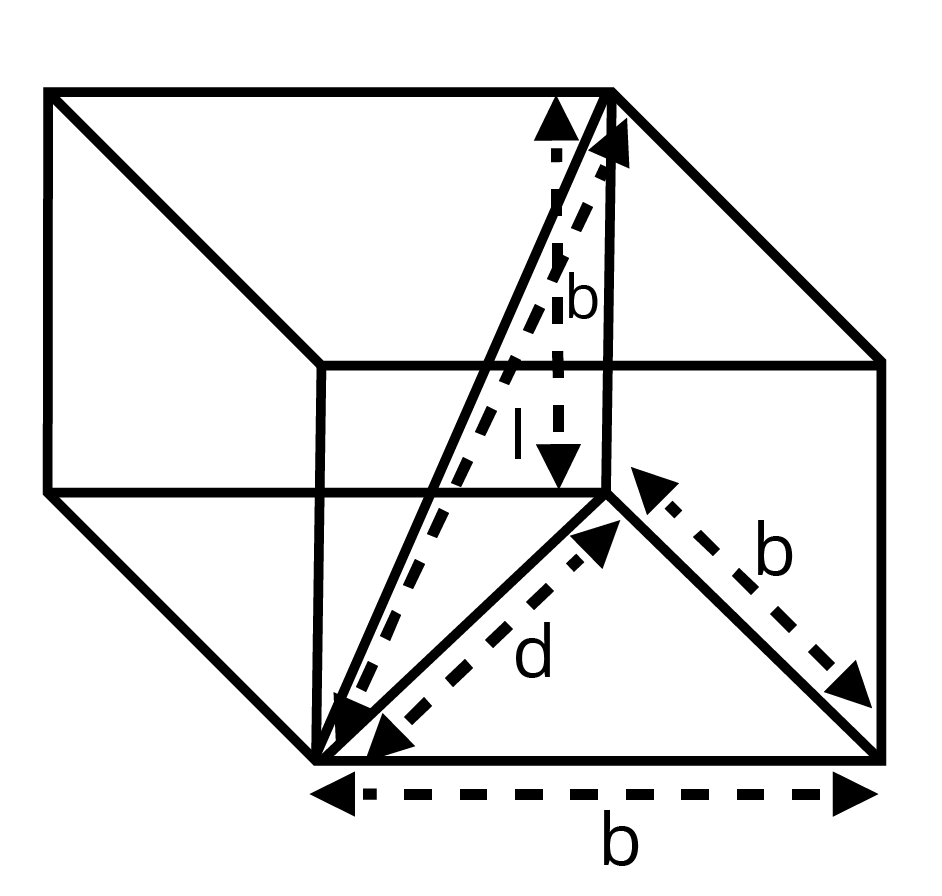
A cube of side \[b\] is shown in the following figure.

\[d=\]Diagonal of one of the six faces of the cube

\[\Rightarrow {{d}^{2}}=\sqrt{{{b}^{2}}+{{b}^{2}}}=\sqrt{2{{b}^{2}}}\]

\[\Rightarrow d=b\sqrt{2}\]

\[l=\] length of the diagonal of the cube

\[{{l}^{2}}=\sqrt{{{d}^{2}}+{{b}^{2}}}\]

\[\Rightarrow {{l}^{2}}=\sqrt{{{\left( \sqrt{2}b \right)}^{2}}+{{b}^{2}}}\]

\[\Rightarrow {{l}^{2}}=\sqrt{2{{b}^{2}}+{{b}^{2}}}\]

\[\Rightarrow {{l}^{2}}=\sqrt{3{{b}^{2}}}\]

\[\Rightarrow l=b\sqrt{3}\]

\[\Rightarrow r=\frac{l}{2}=\frac{b\sqrt{2}}{2}\] is the difference between the centre of the cube and one of the eight vertices.

The electric potential \[V\] at the centre of the cube is due to the presence of eight charges at the vertices.

\[V=\frac{8q}{4\pi {{\in }_{0}}}\]

\[\Rightarrow V=\frac{8q}{4\pi {{\in }_{0}}\left( \frac{b\sqrt{3}}{2} \right)}\]

\[\Rightarrow V=\frac{4q}{\sqrt{3}\pi {{\in }_{0}}b}\]

Therefore, the potential at the centre of the cube is \[\frac{4q}{\sqrt{3}\pi {{\in }_{0}}b}\].

The electric field at the centre of the cube, due to the eight charges, gets cancelled. This is because the charges are distributed symmetrically with respect to the cube. 

Therefore, the electric field is zero at the centre.

9. Two tiny spheres carrying charges \[1.5\mu C\] and \[2.5\mu C\] are located \[30cm\] apart. Find the potential and electric field:

(a) At the mid-point of the line joining the two charges, and

Ans: The charges are depicted as:

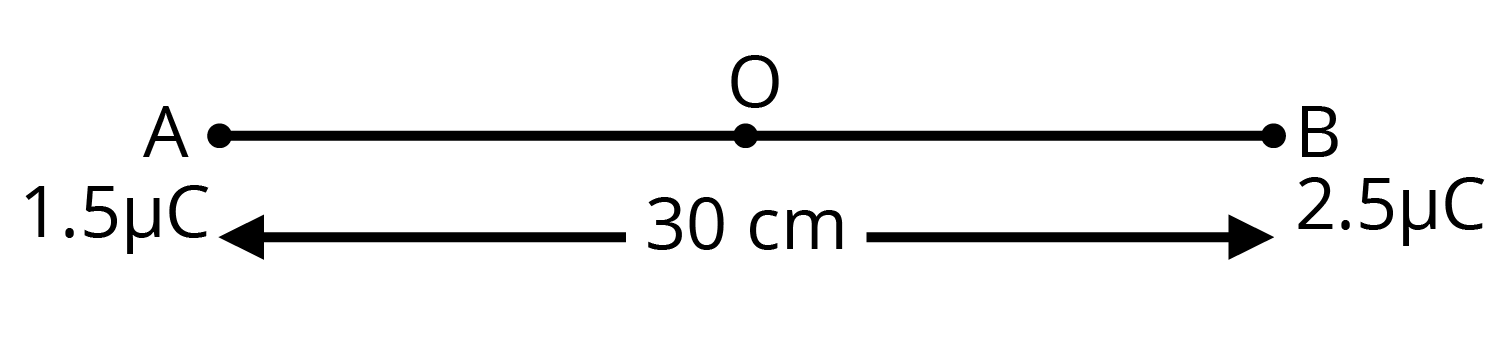
Two charges placed at points \[A\] and \[B\] are depicted in the provided figure. O is the mid-point of the line joining the two charges.

Magnitude of charge located at \[A\], \[{{q}_{1}}=1.5\mu C\]

Magnitude of charge located at \[B\], \[{{q}_{2}}=2.5\mu C\]

Distance between the two charges, \[d=30cm=0.3m\]

Let \[{{V}_{1}}\]and  \[{{E}_{1}}\] are electric potential and electric field respectively at O.

\[{{V}_{1}}=\] Potential due to charge at \[A+\]Potential due to charge at \[B\]

\[{{V}_{1}}=\frac{{{q}_{1}}}{4\pi {{\in }_{0}}\left( \frac{d}{2} \right)}+\frac{{{q}_{2}}}{4\pi {{\in }_{0}}\left( \frac{d}{2} \right)}=\frac{1}{4\pi {{\in }_{0}}\left( \frac{d}{2} \right)}\left( {{q}_{1}}+{{q}_{2}} \right)\]

Where,

\[{{\in }_{0}}=\]permittivity of free space

Where, \[\frac{1}{4\pi {{\in }_{0}}}=9\times {{10}^{9}}N{{C}^{2}}{{m}^{-2}}\]

\[{{V}_{1}}=\frac{9\times {{10}^{9}}\times {{10}^{-5}}}{\left( \frac{0.30}{2} \right)}\left( 2.5+1.5 \right)\]

\[{{V}_{1}}=2.4\times {{10}^{5}}V\]

\[{{E}_{1}}=\] Electric field due to \[{{q}_{2}}\] \[-\]Electric field due to \[{{q}_{1}}\]

\[\Rightarrow {{E}_{1}}=\frac{{{q}_{2}}}{4\pi {{\in }_{0}}{{\left( \frac{d}{2} \right)}^{2}}}-\frac{{{q}_{1}}}{4\pi {{\in }_{0}}{{\left( \frac{d}{2} \right)}^{2}}}\]

\[\Rightarrow {{E}_{1}}=\frac{9\times {{10}^{9}}}{{{\left( \frac{0.30}{2} \right)}^{2}}}\times {{10}^{6}}\times \left( 2.5-1.5 \right)\]

\[\Rightarrow {{E}_{1}}=4\times {{10}^{5}}V{{m}^{-1}}\]

Therefore, the potential at mid-point is \[2.4\times {{10}^{5}}V\] and the electric field at mid-point is \[4\times {{10}^{5}}V{{m}^{-1}}\]. The field is directed from the larger charge to the smaller charge

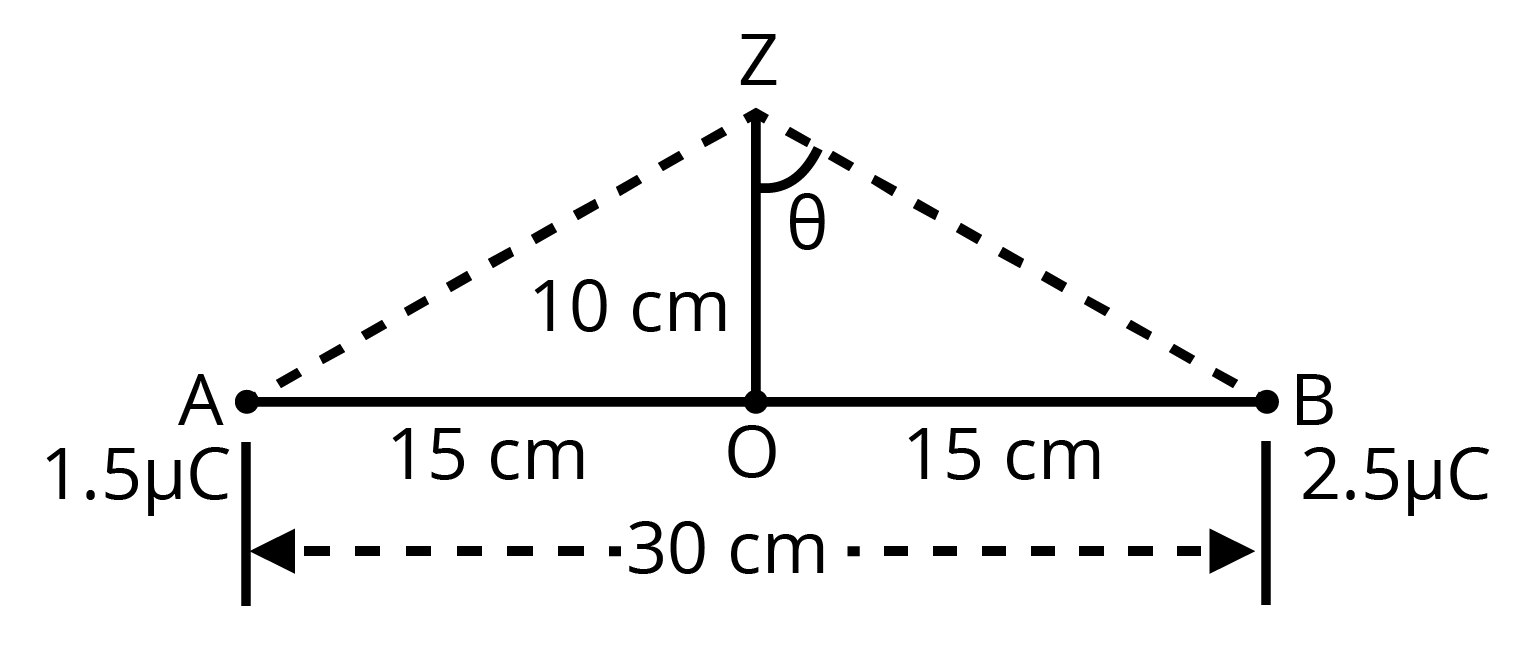
(b) At a point \[10cm\] from this midpoint in a plane normal to the line passing through the mid-point.

Ans: Consider a point \[Z\]such that the normal distance \[OZ=10cm=0.1m\] as shown in the following figure.

\[{{V}_{2}}\] and \[{{E}_{2}}\] are the electric potential and electric field respectively at \[Z\]. It can be observed from the figure that distance,

\[BZ=AZ=\sqrt{{{\left( 0.1 \right)}^{2}}+{{\left( 0.15 \right)}^{2}}}=0.18m\]

\[{{V}_{2}}=\] Electric potential due to \[A+\]Electric potential due to point \[B\]

\[\Rightarrow {{V}_{2}}=\frac{{{q}_{2}}}{4\pi {{\in }_{0}}\left( AZ \right)}+\frac{{{q}_{1}}}{4\pi {{\in }_{0}}\left( BZ \right)}\]

\[\Rightarrow {{V}_{2}}=\frac{9\times {{10}^{9}}\times {{10}^{-5}}}{0.18}\left( 1.5+2.5 \right)\]

\[\Rightarrow {{V}_{2}}=2\times {{10}^{5}}V\]

Electric field due to \[{{q}_{1}}\] at \[Z\],

\[{{E}_{A}}=\frac{{{q}_{1}}}{4\pi {{\in }_{0}}\left( AZ \right)}\]

\[\Rightarrow {{E}_{A}}=\frac{9\times {{10}^{9}}\times 1.5\times {{10}^{-5}}}{0.18}\]

\[\Rightarrow {{E}_{A}}=0.416\times {{10}^{6}}V/m\]

Electric field due to \[{{q}_{2}}\] at \[Z\],

\[{{E}_{B}}=\frac{{{q}_{2}}}{4\pi {{\in }_{0}}{{\left( BZ \right)}^{2}}}\]

\[\Rightarrow {{E}_{B}}=\frac{9\times {{10}^{9}}\times 2.5\times {{10}^{-5}}}{{{\left( 0.18 \right)}^{2}}}\]

\[\Rightarrow {{E}_{B}}=0.69\times {{10}^{6}}V/m\]

The resultant field intensity at \[Z\]

\[E=\sqrt{{{E}^{2}}_{A}+{{E}^{2}}_{B}+2{{E}_{A}}{{E}_{B}}\cos 2\theta }\]

Where, \[2\theta \] is the angle, \[\angle AZB\]

From the given figure, we obtain

\[\cos \theta =\frac{0.10}{0.18}=\frac{5}{9}=0.5556\]

\[\Rightarrow \theta ={{\cos }^{-1}}0.5556={{56.25}^{\circ }}\]

\[\Rightarrow 2\theta ={{112.5}^{\circ }}\]

\[\Rightarrow \cos 2\theta =-0.38\]

\[E=\sqrt{{{\left( 0.416\times {{10}^{6}} \right)}^{2}}\times 2\times 0.416\times 0.69\times {{10}^{12}}\times \left( -0.38 \right)}\]

\[\Rightarrow E=6.6\times {{10}^{5}}V{{m}^{-1}}\]

Therefore, the potential at a point \[10cm\] (perpendicular to the mid-point) is $ 2.0 \times {{10}^{5}} V$ and the electric field is \[6.6\times {{10}^{5}}V{{m}^{-1}}\].

10. 

(a) Show that the normal component of electrostatic field has a discontinuity from one side of a charged surface to another given by \[\left( \overline{{{E}_{2}}}-\overline{{{E}_{1}}} \right)\cdot \hat{n}=\frac{\sigma }{{{\in }_{0}}}\]. Where \[\hat{n}\] is a unit vector normal to the surface at a point and \[\sigma \] is the surface charge density at that point. (The direction of \[\hat{n}\] is from side \[1\]to side \[2\]). Hence show that just outside a conductor, the electric field is \[\frac{{\hat{n}}}{{{\in }_{0}}}\].

Ans: Electric field on one side of a charged body is \[{{E}_{1}}\] and electric field on the other side of the same body is \[{{E}_{2}}\]. If an infinite plane charged body has a uniform thickness, then electric field due to one surface of the charged body is given by,

\[\overline{{{E}_{1}}}=-\frac{\sigma }{2{{\in }_{0}}}\hat{n}\]

Where,

\[\hat{n}=\] Unit vector normal to the surface at a point 

\[\sigma =\]Surface charge density at that point 

Electric field due to the other surface of the charge body,

\[\overline{{{E}_{2}}}=-\frac{\sigma }{2{{\in }_{0}}}\hat{n}\]

Electric field at any point due to the two surfaces,

$\left( \overline{{{E}_{2}}}-\overline{{{E}_{1}}} \right)=\frac{\sigma }{2{{\in }_{0}}}\hat{n}+\frac{\sigma }{2{{\in }_{0}}}\hat{n}+\frac{\sigma }{{{\in }_{0}}}\hat{n} $

$\Rightarrow \left( \overline{{{E}_{2}}}-\overline{{{E}_{1}}} \right)\cdot \hat{n}=\frac{\sigma }{{{\in }_{0}}} $

Since inside a closed conductor, \[\overline{{{E}_{1}}}=0\],

\[\overline{E}=\overline{{{E}_{2}}}=-\frac{\sigma }{2{{\in }_{0}}}\hat{n}\]

Therefore, the electric field just outside the conductor is \[\frac{\sigma }{{{\in }_{0}}}\hat{n}\].

(b) Show that the tangential component of an electrostatic field is continuous from one side of a charged surface to another. 

Ans: When a charge particle is moved from one point to the other on a closed loop, the work done by the electrostatic field is zero. Hence, the tangential component of an electrostatic field is continuous from one side of a charged surface to the other.

11. A long charged cylinder of linear charge density \[\lambda \] is surrounded by a hollow co-axial conducting cylinder. What is the electric field in the space between the two cylinders?

Ans: Charge density of the long, charged cylinder of length \[L\] and radius \[r\] is \[\lambda \].

Another cylinder of the same length surrounds the previous cylinder. The radius of this cylinder is \[R\].

Let \[E\] be the electric field produced in the space between the two cylinders.

Electric flux through the Gaussian surface is given by Gauss's theorem as, \[\phi =E\left( 2\pi d \right)L\]

Where, 

\[d=\]Distance of a point from the common axis of the cylinders. Let \[q\]be the total charge on the cylinder.

It can be written as

\[\Rightarrow \phi =E\left( 2\pi d \right)L=\frac{q}{{{\in }_{0}}}\]

Where,

\[q=\] Charge on the inner sphere of the outer cylinder

\[{{\in }_{0}}=\]permittivity of free space

\[\Rightarrow E\left( 2\pi d \right)L=\frac{\lambda L}{{{\in }_{0}}}\]

\[\Rightarrow E=\frac{\lambda }{2\pi {{\in }_{0}}d}\]

Therefore, the electric field in the space between the two cylinders is \[\frac{\lambda }{2\pi {{\in }_{0}}d}\].

12. In a hydrogen atom, the electron and proton are bound at a distance of about \[0.53{{A}^{\circ }}\].

(a) Estimate the potential energy of the system in \[eV\], taking the zero of the potential energy at infinite separation of the electron from the proton.

Ans: The distance between the electron-proton of a hydrogen atom is given as, \[d=0.53\overset{{}^\circ }{\mathop{A}}\,\].

Charge on an electron, \[{{q}_{1}}=1.6\times {{10}^{-19}}C\]

Charge on a proton, \[{{q}_{2}}=+1.6\times {{10}^{-19}}C\]

Potential at infinity is zero.

\[=0-\frac{{{q}_{1}}{{q}_{2}}}{4\pi {{\in }_{0}}d}\]

Potential energy of the system, \[p-e=\] Potential energy at infinity – Potential energy t distance, \[d\]

Where,

\[{{\in }_{0}}\] is the permittivity of free space

We can further express,

\[\frac{1}{4\pi {{\in }_{0}}}=9\times {{10}^{9}}N{{m}^{2}}{{C}^{-2}}\]

\[\Rightarrow \frac{1}{4\pi {{\in }_{0}}}=0-\frac{9\times {{10}^{9}}\times {{\left( 1.6\times {{10}^{-19}} \right)}^{2}}}{0.53\times {{10}^{10}}}\]

\[Potential\,Energy=\frac{-43.7\times {{10}^{-19}}}{1.6\times {{10}^{-19}}}\]

\[\Rightarrow Potential\,Energy=-27.2eV\]

Therefore, the potential energy of the system is \[-27.2eV\].

(b) What is the minimum work required to free the electron, given that its kinetic energy in the orbit is half the magnitude of potential energy obtained in (a)

Ans: Kinetic energy can be given as half times the magnitude of potential energy.

Kinetic Energy\[=\frac{1}{2}\times \left( -27.2eV \right)=13.6eV\]

Total energy \[=13.6eV\]

Therefore, the minimum work required to free the electron is \[13.6eV\].

(c) What are the answers to (a) and (b) above if the zero of potential energy is taken at \[1.06\overset{{}^\circ }{\mathop{A}}\,\] separation?

Ans: When zero of potential energy is taken, \[{{d}_{1}}=1.06\overset{{}^\circ }{\mathop{A}}\,\]

$\therefore$ Potential energy of the system = Potential energy at \[{{d}_{1}}\]\[-\]Potential energy at \[d\].

\[Potential\,Energy\,of\,the\,\text{ }system=\frac{{{q}_{1}}{{q}_{2}}}{4\pi {{\in }_{0}}{{d}_{1}}}-27.2eV\]

\[\Rightarrow Potential\,Energy\,of\,the\,\text{ }system=\frac{9\times {{10}^{9}}\times {{\left( 1.6\times {{10}^{-19}} \right)}^{2}}}{1.06\times {{10}^{-10}}}-27.2eV\]

\[\Rightarrow 21.73\times {{10}^{-10}}J-27.2eV\]

\[\Rightarrow 13.58eV-27.2eV\]

\[\Rightarrow 13.6eV\]

13. Two charges \[-q\] and \[+q\] are located at points \[\left( 0,0,-a \right)\] and \[\left( 0,0,a \right)\], respectively.

(a) What is the electrostatic potential at these points?

Ans:  In this situation, charge \[-q\] is located at \[\left( 0,0,-a \right)\] and charge \[+q\] is located at \[\left( 0,0,a \right)\]. Therefore, they form a dipole. Point \[\left( 0,0,z \right)\] is on the axis of this dipole and point \[\left( x,y,0 \right)\] is normal to the axis of the dipole. Hence, the electrostatic potential at point \[\left( x,y,0 \right)\] is zero. Electrostatic potential at point \[\left( 0,0,z \right)\] is given by,

\[V=\frac{1}{4\pi {{\in }_{0}}}\left( \frac{q}{z-a} \right)+\frac{1}{4\pi {{\in }_{0}}}\]

\[\Rightarrow V=\frac{q\left( z+a-z+a \right)}{4\pi {{\in }_{0}}\left( {{z}^{2}}-{{a}^{2}} \right)}\]

\[\Rightarrow V=\frac{2qa}{4\pi {{\in }_{0}}\left( {{z}^{2}}-{{a}^{2}} \right)}\]

\[\Rightarrow V=\frac{p}{4\pi {{\in }_{0}}\left( {{z}^{2}}-{{a}^{2}} \right)}\]

Where,

\[{{\in }_{0}}=\]permittivity of free space

\[p=\]Dipole moment of the system of two charges \[=2qa\]

(b) Obtain the dependence of potential on the distance \[r\] of a point from the origin when \[\frac{r}{a}>>1\].

Ans: Distance \[r\] is much greater than half of the distance between the two charges. Therefore, the potential \[\left( V \right)\] at a distance \[r\] is inversely proportional to the square of the distance.

i.e., \[4\propto \frac{1}{{{r}^{2}}}\]

(c) How much work is done in moving a small test charge from the point \[1.06{{A}^{\circ }}\] to \[\left( -7,0,0 \right)\] along the x-axis? Does the answer change if the path of the test charge between the same points is not along the x-axis?

Ans:  Zero

The answer does not change if the path of the test charge is not along the x-axis.

A test charge is moved from point \[\left( 5,0,0 \right)\] to point \[\left( -7,0,0 \right)\] along the x-axis. Electrostatic potential \[{{V}_{1}}\] at point \[\left( 5,0,0 \right)\] is given by,

\[{{V}_{1}}=\frac{-q}{4\pi {{\in }_{0}}}\frac{1}{\sqrt{{{\left( 5-0 \right)}^{2}}-{{\left( -a \right)}^{2}}}}+\frac{q}{4\pi {{\in }_{0}}}\frac{1}{\sqrt{{{\left( 5-0 \right)}^{2}}-{{\left( -a \right)}^{2}}}}\]

\[\Rightarrow {{V}_{1}}=\frac{-q}{4\pi {{\in }_{0}}\sqrt{25+{{a}^{2}}}}+\frac{q}{4\pi {{\in }_{0}}\sqrt{25+{{a}^{2}}}}\]

\[\Rightarrow {{V}_{1}}=0\]

Electrostatic potential, \[{{V}_{2}}\] at point \[\left( -7,0,0 \right)\] is given by,

\[{{V}_{2}}=\frac{-q}{4\pi {{\in }_{0}}}\frac{1}{\sqrt{{{\left( 7 \right)}^{2}}-{{\left( -a \right)}^{2}}}}+\frac{q}{4\pi {{\in }_{0}}}\frac{1}{\sqrt{{{\left( -7 \right)}^{2}}-{{\left( -a \right)}^{2}}}}\]

\[\Rightarrow {{V}_{2}}=\frac{-q}{4\pi {{\in }_{0}}\sqrt{49+{{a}^{2}}}}+\frac{q}{4\pi {{\in }_{0}}\sqrt{49+{{a}^{2}}}}\]

\[\Rightarrow {{V}_{2}}=0\]

Therefore, no work is done in moving a small test charge from point \[\left( 5,0,0 \right)\] to point \[\left( -7,0,0 \right)\] along the x-axis.

The answer will not change because work done by the electrostatic field in moving a test charge between the two points is not dependent of the path connecting the two points.

14. Figure 2.34 shows a charge array known as an electric quadrupole. For a point on the axis of the quadrupole, obtain the dependence of potential on \[r\] for \[\frac{r}{a}>>1\] and contrast your results with that due to an electric dipole, and an electric monopole (i.e., a single charge)

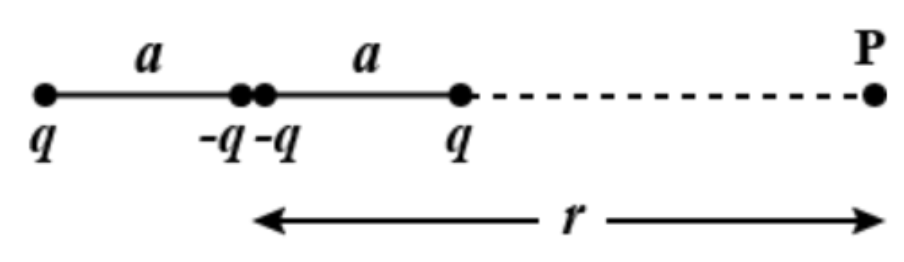
Ans: Four charges of the same magnitude are placed at points \[X\], \[Y\] and \[Z\] respectively, as depicted in the following figure.

A point is located at \[P\], which is \[r\] distance away from point \[Y\]. The system of charges forms an electric quadrupole.

It can be considered that the system of the electric quadrupole has three charges

Charge \[+q\] placed at point \[X\]

Charge \[-2q\] placed at point \[Y\]

Charge \[+q\] placed at point \[Z\]

\[XY=YZ=a\]

\[YP=r\]

\[PX=r+a\]

\[PZ=r-a\]

Electrostatic potential that is caused by the system of three charges at point \[P\] can be given by,

\[V=\frac{1}{4\pi {{\in }_{0}}}\left[ \frac{q}{XP}-\frac{2q}{YP}+\frac{q}{ZP} \right]\]

\[\Rightarrow V=\frac{1}{4\pi {{\in }_{0}}}\left[ \frac{q}{r+a}-\frac{2q}{r}+\frac{q}{r-a} \right]\]

\[\Rightarrow V=\frac{q}{4\pi {{\in }_{0}}}\left[ \frac{r\left( r-a \right)-2\left( r+a \right)\left( r-a \right)+r\left( r+a \right)}{r\left( r+a \right)\left( r-a \right)} \right]\]

\[\Rightarrow V=\frac{q}{4\pi {{\in }_{0}}}\left[ \frac{{{r}^{2}}-ra-2{{r}^{2}}+2{{a}^{2}}+{{r}^{2}}+ra}{r\left( {{r}^{2}}-{{a}^{2}} \right)} \right]\]

\[\Rightarrow V=\frac{q}{4\pi {{\in }_{0}}}\left[ \frac{2{{a}^{2}}}{r\left( {{r}^{2}}-{{a}^{2}} \right)} \right]\]

\[\Rightarrow V=\frac{2q{{a}^{2}}}{4\pi {{\in }_{0}}{{r}^{3}}\left( 1-\frac{{{a}^{2}}}{{{r}^{2}}} \right)}\]

Since \[\frac{r}{a}>>1\]

\[\frac{{{r}^{2}}}{{{a}^{2}}}\] is taken as negligible.

\[V=\frac{2q{{a}^{2}}}{4\pi {{\in }_{0}}{{r}^{3}}}\]

It can be inferred that potential, \[V\propto \frac{1}{{{r}^{3}}}\]

But it is known that for a dipole, \[V\propto \frac{1}{{{r}^{2}}}\]

And, for a monopole, \[V\propto \frac{1}{r}\]

15. An electrical technician requires a potential difference of $2\mu F$ in a circuit across a potential difference of  \[1kV\]. A large number of  $2\mu F$ capacitors are available to him, each of which can withstand a potential difference of not more than $400V$. Suggest a possible arrangement that requires the minimum number of capacitors.

Ans: Total required capacitance is given as, $C=2\mu F$ 

Potential difference is given as, $V=1kV=1000V$

Capacitance of each capacitor, ${{C}_{1}}=1\mu F$

Each capacitor can hold a potential difference,

 ${{V}_{1}}=400V$

$\frac{1000}{400}=2.5$

Let us suppose a number of capacitors are connected in series and these series and these series circuits are connected in parallel (row) to each other. The potential difference across each row must be $1000V$ and the potential difference across each capacitor must be $400V$. Hence, the number of capacitors in each row is given as

Therefore, there are three capacitors in each row. 

Capacitance of each row$=\frac{1}{1+1+1}=\frac{1}{3}\mu F$

$\frac{1}{3}+\frac{1}{3}+\frac{1}{3}+.....\text{n terms = }\frac{n}{3}$

However, capacitance of the circuit is given as $2\mu F$.

$\therefore \frac{n}{3}=2$

$N=6$

Let there be $n$ rows, each having three capacitors, which are connected in parallel. Hence, equivalent capacitance of the circuit is given as

Hence, $6$ rows of three capacitors are present in the circuit. A minimum of $6\times 3$ i.e.,$18$ capacitors are required for the given arrangement.

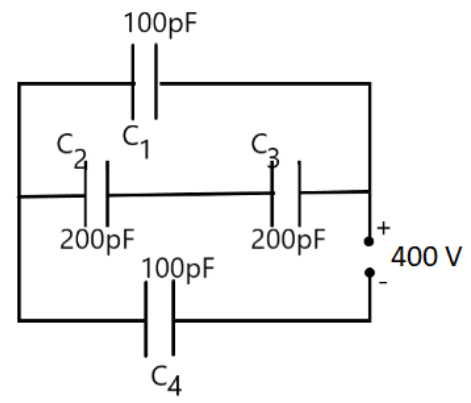
16. Obtain the equivalent capacitance of the network in Fig. 2.35. For a $300V$ supply, determine the charge and voltage across each capacitor.

Ans: Capacitance of capacitor ${{C}_{1}}$ is given as $100pF$.

Capacitance of capacitor ${{C}_{2}}$ is given as $200pF$.

Capacitance of capacitor ${{C}_{3}}$ is given as $200pF$.

Capacitance of capacitor ${{C}_{4}}$ is given as $200pF$.

Supply potential, $V=300V$

Capacitors ${{C}_{2}}$ and ${{C}_{3}}$ are connected in series. Let their equivalent capacitance be C1

$\therefore \frac{1}{{{C}^{1}}}=\frac{1}{200}+\frac{1}{200}=\frac{2}{200}\Rightarrow {{C}^{1}}=100pF$

Capacitors ${{C}^{1}}$ and $C'$ are parallel. Let their equivalent capacitance be ${{C}^{n}}$

$\therefore {{C}^{n}}={{C}^{1}}+{{C}_{1}}=100+100=200pF$

${{C}^{n}}$ and ${{C}_{4}}$ are connected in series. Let their equivalent capacitance be $C$.

$\therefore \frac{1}{C}=\frac{1}{{{C}^{n}}}+\frac{1}{{{C}_{4}}}=\frac{1}{200}+\frac{1}{100}=\frac{2+1}{200}\Rightarrow C=\frac{200}{3}pF$

Hence, the equivalent capacitance of the circuit is $\frac{200}{3}pF$.

 Potential difference across

${{C}^{n}}={V}''$

Potential difference across ${{C}_{4}}={{V}_{4}}$

$\therefore {{V}^{5}}+{{V}_{4}}=V=300V$

Charge on ${{C}_{1}}$ is given by,

${{Q}_{4}}=CV=\frac{200}{3}\times {{10}^{-12}}\times 300=2\times {{10}^{-8}}C$

$\therefore {{V}_{4}}=\frac{{{Q}_{4}}}{{{C}_{4}}}=\frac{2\times {{10}^{-8}}}{100\times {{10}^{-12}}}=200V$

$\therefore$ Voltage across ${{C}_{1}}$ is given by,

${{V}_{1}}=V-{{V}_{4}}=300-200=100V$

Hence, the potential difference, ${{V}_{1}}$ across ${{C}_{1}}$ is $100V$. Charge on ${{C}_{1}}$ is given by, 

${{Q}_{1}}={{C}_{1}}{{V}_{1}}=100\times {{10}^{-12}}\times 100={{10}^{-8}}$

Now,  ${{C}_{2}}$ and ${{C}_{3}}$ having the same capacitance have a potential difference of $100V$together. Since ${{C}_{2}}$ and ${{C}_{3}}$ are in series, the potential difference across ${{C}_{2}}$ and ${{C}_{3}}$ is given by,

${{V}_{2}}={{V}_{3}}=50V$

Therefore, charge on ${{C}_{2}}$ is given by,

${{Q}_{2}}={{C}_{2}}{{V}_{2}}=200\times {{10}^{-12}}\times 50={{10}^{-8}}C$

And charge on ${{C}_{3}}$ is given by,

${{Q}_{3}}={{C}_{3}}{{V}_{3}}=200\times {{10}^{-12}}\times 50={{10}^{-8}}C$

Therefore, the equivalent capacitance of the given circuit is  $\frac{200}{3}\text{pF with}$

${{Q}_{1}}={{10}^{-8}}C{{V}_{1}}=100V$

${{Q}_{2}}={{10}^{-8}}C{{V}_{2}}=50V$

${{Q}_{3}}={{10}^{-8}}C{{V}_{3}}=50V$

${{Q}_{4}}=2\times {{10}^{-8}}C{{V}_{4}}=200V$

17. The plates of a parallel plate capacitor have an area of $90c{{m}^{2}}$ each and are separated by $2.5mm$. The capacitor is charged by connecting it to a $400V$ supply.

(a) How much electrostatic energy is stored by the capacitor?

Ans: Area of the plates of a parallel plate capacitor is given as, $A=90c{{m}^{2}}=90\times {{10}^{-4}}{{m}^{2}}$

Distance between the plates, $d=2.5mm=2.5\times {{10}^{-3}}m$

Potential difference across the plates, $V=400V$

Capacitance of the capacitor is given by the relation,

$C=\frac{A{{\varepsilon }_{0}}}{d}$

Electrostatic energy stored in the capacitor is given by the relation, ${{E}_{1}}=\frac{1}{2}C{{V}^{2}}$

$=\frac{1}{2}\frac{{{\varepsilon }_{0}}A}{d}{{V}^{2}}$

Where, 

${{\varepsilon }_{0}}=$ Permittivity of free space$=8.85\times {{10}^{-12}}{{C}^{2}}{{N}^{-1}}{{m}^{-2}}$

$\therefore {{E}_{1}}=\frac{1\times 8.85\times {{10}^{-12}}\times 90\times {{10}^{-4}}\times {{\left( 400 \right)}^{2}}}{2\times 2.5\times {{10}^{-3}}}=2.55\times {{10}^{-6}}J$

Hence, the electrostatic energy stored by the capacitor is $2.55\times {{10}^{-6}}J$.

(b) View this energy as stored in the electrostatic field between the plates, and obtain the energy per unit volume $u$. Hence arrive at a relation between $u$ and the magnitude of electric field $E$ between the plates.

Ans: Volume of the given capacitor,

${{V}^{1}}=A\times d=90\times {{10}^{-4}}\times 25\times {{10}^{-3}}=2.25\times {{10}^{-4}}{{m}^{3}}$

Energy stored in the capacitor per unit volume is given by,

$u=\frac{{{E}_{1}}}{{{V}_{1}}}=\frac{2.25\times {{10}^{-6}}}{2.25\times {{10}^{-4}}}=0.113J{{m}^{-3}}$

Again, $u=\frac{{{E}_{1}}}{{{V}_{1}}}$

Where,

$\frac{V}{d}=$Electric intensity$=E$

$\therefore u=\frac{1}{2}{{\varepsilon }_{0}}{{E}^{2}}$, which is the required energy stored.

18. A $4\mu F$ capacitor is charged by a $200V$ supply. It is then disconnected from the supply, and is connected to another uncharged $2\mu F$ capacitor. How much electrostatic energy of the first capacitor is lost in the form of heat and electromagnetic radiation?

Ans: Given that,

Capacitance of a charged capacitor,  ${{C}_{1}}=4\mu F=4\times {{10}^{-5}}F$

Supply voltage, ${{V}_{1}}=200V$

Electrostatic energy stored in ${{C}_{1}}$ is given by,

${{E}_{1}}=\frac{1}{2}{{C}_{1}}{{V}_{1}}^{2}=\frac{1}{2}\left( 4\times {{10}^{-5}} \right)\times {{\left( 200 \right)}^{2}}=8\times {{10}^{-2}}J$

Capacitance of an uncharged capacitor, ${{C}_{2}}=2\mu F=2\times {{10}^{-6}}F$

When ${{C}_{2}}$ is connected to the circuit, the potential acquired by it is ${{V}_{2}}$,

$\therefore {{V}_{2}}\left( {{C}_{1}}+{{C}_{2}} \right)={{C}_{1}}{{V}_{1}}$

$\Rightarrow {{V}_{2}}\left( 4+2 \right)\times {{10}^{-5}}=4\times {{10}^{-6}}\times 200$

$\Rightarrow {{V}_{2}}=\frac{400}{3}V$

According to the conservation of charge, initial charge on capacitor ${{C}_{1}}$ is equal to the final charge on capacitors ${{C}_{1}}$ and ${{C}_{2}}$.

Electrostatic energy for the combination of two capacitors is given by,

\[{{E}_{2}}=\frac{1}{2}\left( {{C}_{1}}+{{C}_{2}} \right){{V}_{2}}^{1}=\frac{1}{2}\left( 2+4 \right)\times {{10}^{-5}}\times {{\left( \frac{400}{3} \right)}^{2}}=5.33\times {{10}^{-2}}J\]

Hence, the amount of electrostatic energy lost by the capacitor ${{C}_{1}}$ is \[5.33\times {{10}^{-2}}J\]. 

19. Show that the force on each plate of a parallel plate capacitor has a magnitude equal to $\frac{1}{2}QE$, where $Q$ is the charge on the capacitor, and $E$ is the magnitude of the electric field between the plates. Explain the origin of the factor $\frac{1}{2}$.

Ans: Let $F$ be the force applied to separate the plates of a parallel plate capacitor by a distance of$\Delta x$. Hence, work done by the force to do so $=F\Delta x$

As a result, the potential energy of the capacitor increases by an amount given as$uA\Delta x$.

Where,

$u=$Energy density

$A=$Area of each plate

$d=$ Distance between the plate

$V=$Potential difference across the plates

The work done will be equal to the increase in the potential energy i.e.,

$F\Delta x=uA\Delta x$

$\Rightarrow F=uA=\left( \frac{1}{2}{{\varepsilon }_{0}}{{E}^{2}} \right)A$

Electric intensity is given by,

$E=\frac{V}{d}$

$\Rightarrow F=\frac{1}{2}{{\varepsilon }_{0}}\left( \frac{V}{d} \right)EA=\frac{1}{2}\left( {{\varepsilon }_{0}}A\frac{V}{d} \right)E$

However, capacitance can be given as, $C=\frac{{{\varepsilon }_{0}}A}{d}$

$\therefore F=\frac{1}{2}\left( CV \right)E$

Charge on the capacitor is given by,

$Q=CV\Rightarrow F=\frac{1}{2}QE$

The physical origin of the factor, $\frac{1}{2}$, in the force formula lies in the fact that just outside the conductor, the field is $E$ and inside it is zero. Hence, it is the average value, $\frac{E}{2}$, of the field that contributes to the force.

20. A spherical capacitor has an inner sphere of radius \[12cm\] and an outer sphere of radius \[13cm\]. The outer sphere is earthed and the inner sphere is given a charge of \[2.5\mu C\]. The space between the concentric spheres is filled with a liquid of dielectric constant \[32\]

(a) Determine the capacitance of the capacitor.

Ans: Given that,

Radius of the inner sphere, \[{{r}_{2}}=12cm=0.12m\]

Radius of the outer sphere, \[{{r}_{1}}=13cm=0.13m\]

Charge on the inner sphere, \[q=2.5\mu C=2.5\times {{10}^{-5}}\]

Dielectric constant of a liquid, \[{{\in }_{r}}=32\]

Capacitance of the capacitor is given by the relation,

\[C=\frac{4\pi {{\in }_{0}}{{r}_{1}}{{r}_{2}}}{{{r}_{1}}-{{r}_{2}}}\]

Where,

\[{{\in }_{0}}=\]Permittivity of free space \[=8.85\times {{10}^{-12}}{{C}^{2}}{{N}^{-1}}{{m}^{-2}}\]

\[V=\frac{1}{4\pi {{\in }_{0}}}9\times {{10}^{9}}N{{m}^{2}}{{C}^{-2}}\]

\[C=\frac{32\times 0.12\times 0.13}{9\times {{10}^{9}}\times \left( 0.13-0.12 \right)}\Rightarrow C=5.5\times {{10}^{-9}}F\]

Hence, the capacitance of the capacitor is approximately \[5.5\times {{10}^{-9}}F\].

(b) What is the potential of the inner sphere?

Ans: Potential of the inner sphere is given as below

\[\frac{q}{C}=\frac{2.25\times {{10}^{-6}}}{5.5\times {{10}^{-9}}}=4.5\times {{10}^{2}}V\]

Hence, the potential of the inner sphere is \[4.5\times {{10}^{2}}V\].

(c) Compare the capacitance of this capacitor with that of an isolated sphere of radius \[12cm\]. Explain why the latter is much smaller.

Ans:  Given that,

Radius of an isolated sphere given, \[r=12\times {{10}^{-2}}m\]

Capacitance of the sphere is given by the relation,

\[{C}'=4\pi {{\in }_{0}}r\]

\[\Rightarrow {C}'=4\pi \times 8.85\times {{10}^{-12}}\times 12\times {{10}^{-12}}\]

\[\Rightarrow {C}'=1.33\times {{10}^{-11}}F\]

The capacitance of the isolated sphere is less in comparison to the concentric spheres. This is because the outer sphere of the concentric spheres is earthed. Hence, the potential difference is less and the capacitance is more than the isolated sphere.

21. Answer carefully

(a) wo large conducting spheres carrying charges \[{{Q}_{1}}\] and \[{{Q}_{2}}\] are brought close to each other. Is the magnitude of electrostatic force between them exactly given by \[\frac{{{Q}_{1}}{{Q}_{2}}}{4\pi {{\in }_{0}}{{r}^{2}}}\], where \[r\] is the distance between their centres?

Ans: The force between two conducting spheres is not exactly the same given by the expression \[\frac{{{Q}_{1}}{{Q}_{2}}}{4\pi {{\in }_{0}}{{r}^{2}}}\], because there is a non-uniform charge distribution on the sphere.

(b) If Coulomb’s law involved \[\frac{1}{{{r}^{3}}}\] dependence (instead of \[\frac{1}{{{r}^{2}}}\]), would Gauss’s law be still true?

Ans: Gauss’s law will not hold true, if Coulomb’s law involved \[\frac{1}{{{r}^{3}}}\] dependence, instead of \[\frac{1}{{{r}^{2}}}\] on \[r\].

(c) A small test charge is released at rest at a point in an electrostatic field configuration. Will it travel along the field line passing through that point?

Ans: Yes, if a small test charge is released at rest at a point in an electric field configuration, then it will travel along the field lines passing through the point, only if the field lines are straight. This is because the field lines give the direction of acceleration and not of velocity.

(d) What is the work done by the field of a nucleus in a complete circular orbit of the electron? What if the orbit is elliptical?

Ans: Whenever the electron completes an orbit, either circular or elliptical, the work done by the field of a nucleus is zero.

(e) We know that the electric field is discontinuous across the surface of a charged conductor. Is electric potential also discontinuous there?

Ans: No Electric field is discontinuous across the surface of a charged conductor. However, electric potential is continuous.

(f) What meaning would you give to the capacitance of a single conductor?

Ans: The capacitance of a single conductor is considered as a parallel plate capacitor with one of its two plates at infinity.

(g) Guess a possible reason why water has a much greater dielectric constant \[=80\] than say, mica \[=6\].

Ans:  Water has an unsymmetrical space as compared to mica. Since it has a permanent dipole moment, it has a greater dielectric constant than mica.

22. Answer the following

a) The top of the atmosphere is at about \[400kV\] with respect to the surface of the earth, corresponding to an electric field that decreases with altitude. Near the surface of the earth, the field is about \[100V{{m}^{-1}}\]. Why then do we not get an electric shock as we step out of our house into the open? (Assume the house to be a steel cage so there is no field inside).

Ans: We do not get an electric shock as we step out of our house because the original equipotential surfaces of open-air changes, thus maintaining our body and the ground at the same potential.

b) A man fixes outside his house one evening a two-metre-high insulating slab carrying on its top a large aluminium sheet of area \[1{{m}^{2}}\]. Will he get an electric shock if he touches the metal sheet next morning?

Ans: Yes, the man will get an electric shock when he touches the metal slab. The steady discharging current in the atmosphere charges up the aluminium sheet. Resulting in a gradual rise in voltage. The rise in the voltage depends on the capacitance of the capacitor formed by the aluminium slab and the ground.

c) The discharging current in the atmosphere due to small conductivity of air is known to be \[1800A\] on an average over the globe. Why then does the atmosphere not discharge itself completely in due course and become electrically neutral? In other words, what keeps the atmosphere charged?

Ans: The occurrence of thunderstorms and lightning charges the atmosphere continuously. Thus, even with the presence of discharging current of \[1800A\], the atmosphere maintains its electrical neutrality.

d) What are the forms of energy into which the electrical energy of the atmosphere is dissipated during a lightning strike? (Hint: The earth has an electric field of about \[100V{{m}^{-1}}\] at its surface in the downward direction, corresponding to a surface charge density\[=-{{10}^{-9}}C{{m}^{-2}}\]. Due to the slight conductivity of the atmosphere up to about \[50km\] (beyond which is a good conductor), about \[1800C\] is pumped every second into the earth as a whole. The earth, however, does not get discharged since thunderstorms and lightning occurring continually all over the globe pump an equal amount of negative charge on the earth.)

Ans: During lightning and thunderstorms, light energy, heat energy, and sound energy are emitted to the atmosphere.

Class 12 Physics Chapter 2 Important Questions

Chapter 12 - Electrostatic Potential and Capacitance

Electrostatic Potential 

• When a unit positive charge is moved from one point to the other in an electric field, then the amount of work done to move that charge against an electrostatic force with zero acceleration is known as electrostatic potential.

• The formula of electrostatic potential is:-

 Electrostatic potential (V) = Work done (W)/Charge(q) 

• Volt (V) is the SI unit of electrostatic potential.

• When a charge of 1 coulomb is moved is an electric field against an electrostatic force, then the amount of work done is 1J, hence the electrostatic potential will be 1JC-1.

Electrostatic Potential Difference 

• When a unit positive charge is moved from say point A to another point say point B against an electrostatic force in an electric field, then the electrostatic potential difference between point A and point B is the amount of work done to move the charge from point A to point B with zero acceleration.

• The formula of electrostatic potential difference is:-

              \[ V_{B}-V_{A}=\frac{W_{AB}}{q}\]

• Another formula of electrostatic potential difference is:-

              \[ V_{B}-V_{A}=\int_{B}^{A}E.dl\]

The potential difference point A and point B can be found with the line integral of the electric field from point A to point B.

• When a point charge q is at any point P and a distance r, then the electrostatic potential is computed:-

              \[V=\frac{1}{4\pi\varepsilon _{o}}.\frac{q}{r}\]

• If the point charge is positive, then the electric potential at that point will be positive. Whereas, when the p[oint charge is negative, then the electric potential at that point will be negative.

• A positive charge travels from higher potential to lower potential when placed in an electric field. Whereas, negative potential travels from lower potential to higher potential when placed in an electric field.

The Formula of Electrostatic Potential Due to an Electric Dipole

(Image will be uploaded)

The formula of electrostatic potential due to an electric dipole at point P is:-

                \[V=\frac{1}{4\pi\varepsilon _{o}}.\frac{pcos\Theta }{r^{2}}\]

Where, is the angle between p and r.

The Formula of Electrostatic Potential of a Thin Charged Spherical Shell

• The formula of the electrostatic potential at a point P inside a thin charged spherical shell that carries charge q and has radius R is:-

\[V=\frac{1}{4\pi\varepsilon _{o}}.\frac{q}{R}\]

• The formula of the electrostatic potential at a point P on the surface of a thin charged spherical shell that carries charge q and has radius R is:-

\[V = \frac{1}{4 \pi \epsilon_{0}} . \frac{q}{R}\]

• The formula of the electrostatic potential at a point P outside the thin charged spherical shell that carries charge q and the distance between the point P outside the shell and the centre of the shell is ‘r’  is:-

\[V = \frac{1}{4 \pi \epsilon_{0}} . \frac{q}{r}\], where r is greater than R.

Electrostatic Potential Energy

• When a charge q is moved from one point to another, the work done by the charge q is stored as electrical potential energy.

• The formula of electrostatic potential energy in a system having two charges namely q1 and q2 is:-

\[U = \frac{1}{4 \pi \epsilon_{0}} . \frac{q_{1}q_{2}}{r}\]

These are the important concepts and formulas that are imperative to the students for solving the electrostatic potential and capacitance class 12 important questions. They can also refer to the NCERT question solutions provided by the expert teachers of Vedantu so that grasping of the conceptual part of Physics becomes easy for them.

Important Related Links for CBSE Class 12 Physics 

Conclusion

Mastering the important questions for CBSE Class 12 Physics Chapter 2 - Electrostatic Potential and Capacitance is crucial for success in the upcoming 2024-25 exams. By thoroughly understanding the concepts and solving these questions, students can strengthen their knowledge, improve problem-solving skills, and gain confidence. These questions cover various aspects of electrostatic potential and capacitance, allowing students to deepen their understanding of the topic. With dedicated practice and thorough preparation using these important questions, students can aim for excellent results and excel in their Physics examinations. So, buckle up and embark on this learning journey to achieve academic excellence.