Master Class 10 Triangles Exercise 6.2 Solutions With Step by Step Guidance
NCERT Solutions For Class 10 Maths Chapter 6 Triangles Exercise 6.2 (2025-26)
FAQs on NCERT Solutions For Class 10 Maths Chapter 6 Triangles Exercise 6.2 (2025-26)
1. Does the Basic Proportionality Theorem (BPT) apply to any line cutting two sides of a triangle?
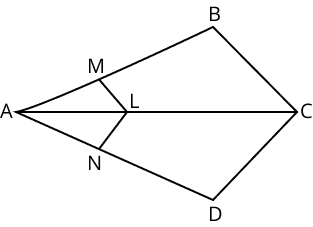
No, the Basic Proportionality Theorem (Thales' Theorem) only applies if the line drawn is parallel to the third side of the triangle. The common mistake is to apply the proportionality rule to any line segment intersecting two sides.
2. Are all similar triangles also congruent?
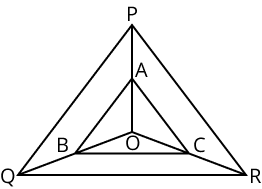
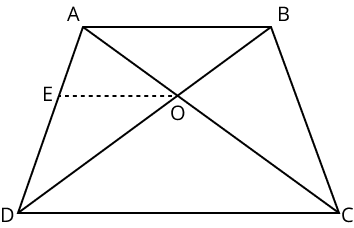
No, similar triangles have the same shape but can be different sizes, whereas congruent triangles must have the exact same shape and size. The confusion occurs because all congruent triangles are similar, but the reverse is not true. For example, two equilateral triangles are always similar, but only congruent if their side lengths are identical.
3. Do NCERT Solutions for Class 10 Maths Chapter 6 just give the final answer?
No, complete NCERT Solutions provide a detailed, step-by-step explanation for every problem, not just the final answer. Many students mistakenly believe that solution guides are simple answer keys without any reasoning.
4. Is the Class 10 Triangles Exercise 6.2 solutions PDF a paid resource?
No, the Free PDF download for NCERT Solutions for Class 10 Maths Triangles Exercise 6.2 can be accessed without any cost. This allows students to study the detailed solutions offline on any device, making exam preparation more flexible and accessible for everyone.
5. Is the SSS (Side-Side-Side) rule the same for similarity and congruence?
No, the SSS rule has a different meaning for similarity versus congruence. For similarity, SSS means the corresponding sides of two triangles are in proportion (i.e., have an equal ratio), whereas for congruence, SSS means the corresponding sides are equal in length.
6. Is the converse of BPT used to find side lengths?
No, the converse of the Basic Proportionality Theorem is specifically used to prove that a line is parallel to a triangle's third side. If you are given that a line divides two sides in the same ratio (e.g., AD/DB = AE/EC), you can conclude that the line DE is parallel to BC.
7. Does using Ex 6.2 Class 10 solutions mean I'm not learning properly?
Not at all; using solutions as a verification tool is a smart study technique, not a shortcut for avoiding work. The myth is that looking at a solution is the same as cheating or failing to learn independently.
The correct method is to attempt the problems from the class 10 maths triangles exercise 6.2 on your own first. If you get stuck or after you have an answer, refer to the solution to check your method and final result. This process helps you pinpoint your mistakes, understand the standard format for writing proofs, and learn more efficient problem-solving strategies.
8. Do I need to prove all three angles are equal for AAA similarity?
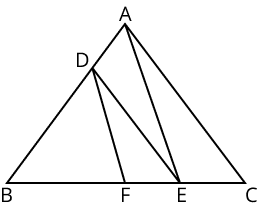
No, you only need to prove that two corresponding angles are equal (the AA similarity criterion). Since the sum of angles in any triangle is always 180°, if two angles of one triangle are equal to two corresponding angles of another, their third angles will automatically be equal. The AA rule is a shortcut for AAA.
9. What is included in the Vedantu Class 10 Triangles Exercise 6.2 Solutions PDF?
The solutions PDF contains methodical, step-by-step derivations for every question in the NCERT exercise, all aligned with the latest CBSE syllabus. It is a common misconception that such resources are just simple answer sheets.
Inside the Free PDF from Vedantu, each solution clearly states the theorem being used (e.g., Theorem 6.1 or 6.2), often includes neatly drawn diagrams to clarify the geometry, and breaks down complex proofs into easy-to-follow logical steps.
10. Are Class 10 Triangles Exercise 6.2 solutions and worksheets the same thing?
No, they serve different functions. NCERT Solutions provide detailed answers to the specific questions in your textbook, which is ideal for checking your work and understanding the correct method. Worksheets, however, typically offer a set of new, additional practice problems on the same concepts to help you test your understanding.




















 Watch Video
Watch Video