




Introduction to Perimeter and Surface Area of a Cube
This article provides information about the perimeter and surface area of a cube, including what they are and the formulas used to calculate them. The perimeter of a cube is simply the distance around the outside of it, while surface area is how much space it takes up. The formula for perimeter and surface area of a cube is 12a and 6$a^2$, where a represents the length of the cube.
So the perimeter is the length of the sides, and the surface area is how much it takes up. It could be helpful to know some formulas to help calculate these.
Surface Area of a Cube
The total area of all the cube's faces makes up the surface area of the object. We are aware that every face in a cube is equal, or that they all have the same area. By multiplying the area of one of its faces by six, we may determine its surface area.
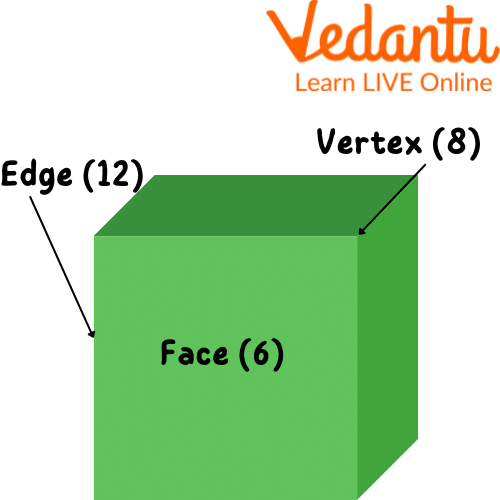
Shape of a Cube
Now let’s learn about cube area and perimeter formulas.
The total area of all the cube's faces makes up the surface area of the object. We must sum the areas of each of the cube's six faces in order to get its surface area because it has six faces.
We are aware that the cube contains a square figure on each face. As a result, the square of one side's length is equal to the area of each face of the cube. If an is used to represent one of the sides' lengths, we get the following:
Area of a cube face $=a^{2}$
If we add the six faces, we have:
$A_{s}=a^{2}+a^{2}+a^{2}+a^{2}+a^{2}+a^{2}$
$A_{s}=6 a^{2}$
where $A_{s}$ represents the surface area and $a$ represents the length of one side of the cube.
Cube Perimeter formula
Let’s discuss how to find the perimeter of a cube formula. The lengths of all the cube's sides, often referred to as its edges, add together to form the perimeter of a cube. There are a total of 12 edges in a cube.
The perimeter of one face of cube formula:
$p=4a$
Additionally, since a cube is a regular shape, all 12 of its edges must be the same length. Taking all of this into account, we can derive the cube perimeter formula shown below:
$p=12 a$
where $a$ is the length of one of the edges of the cube.
Now we have command over the cube area and perimeter formula. Let’s see some solved examples based on it.
Solved Examples
Q1. The perimeter of a cube is 36 cm. Find the surface area of the cube.
Perimeter of a cube = 12a (a = side length)
Ans: Given that 12a = 36
$a=\dfrac{36}{12}$
$=3 \mathrm{~cm}$
Surface Area $=6 (a^2) =6 \times (3^2)$
$=6 \times 9$
$=54 \mathrm{cm}^{2}$
Q2. Find the perimeter of a cube having edges of a length of 5m.
Ans: Put length $a=5$ in the perimeter formula:
$p=12 a$
$p=12(5)$
$p=60 \mathrm{~m}$
The perimeter is equal to $60 \mathrm{~m}$.
Q3. Find the length of the sides of a cube that has a perimeter of $120 \mathrm{~m}$.
Ans: To find the length of the sides or edges, we have to use $p=120$ and solve for $a$ :
$p=12 a$
$120=12 a$
$a=\dfrac{120}{12}$
$a=10 m$
The sides have a length of 10m.
Q4. What will be the surface area of a cube if it has sides of a length of 10m?
Ans: Put $a=10$ in the surface area formula
$A_{s}=6 a^{2}$
$A_{s}=6(10)^{2}$
$A_{s}=6(100)$
$A_{s}=600 m^{2}$
The surface area is $600 \mathrm{~m}^{2}$.
Q5. Find the side length of a cube if it has a surface area of $240 \mathrm{~m}^{2}$.
Ans: Put the surface area in the formula and solve
$A_{s}=6 a^{2}$
$240=6 a^{2}$
$\dfrac{240}{6}=a^{2}$
$40=a^{2}$
$a=6.32 m$
The length of the sides is $6.32 \mathrm{~m}$.
Practice Questions
Q1. What is the length of the sides of a cube that has a perimeter of 144m?
Ans: 12 $m$
Q2. If a cube has sides of length 4m, what is its surface area?
Ans: 96 $m^2$
Q3. If a cube has a surface area of 54m2, what is the length of its sides?
Ans: 3 $m$
Q4. If the perimeter of one face of a cube is 20cm, then its surface area is
Ans: 150 $cm^2$
Q5. Each edge in a cube is 5 cm. What is the surface area in square cm?
Ans: 150 $cm^2$
Summary
One of the most prevalent three-dimensional solid objects is the cube. The length of each side of a cube is its defining property. 6 faces, 12 edges, and 8 vertices make up a cube. Examples of these figures in everyday life include the Rubik's cube and a conventional 6-sided dice. We discussed in the article the formula of perimeter of the cube as well as area.
When we wish to measure a two-dimensional quantity in the cube, the surface area is a measurement that might be helpful. The perimeter of a cube is equal to the total of its individual sides, commonly known as the cube's edges, much like the perimeter of a square is equal to the sum of its side lengths.

Real-life Examples of a Cube
FAQs on How to Find Cube Area and Cube Perimeter Formula
1. What are the basic formulas for a cube's perimeter and surface area?
For a cube with a side length denoted as 'a', the two fundamental formulas are:
- Perimeter of Cube: The total length of all 12 edges combined, calculated as P = 12a.
- Total Surface Area of Cube: The sum of the areas of all six faces, calculated as TSA = 6a².
2. What is the difference between Lateral Surface Area (LSA) and Total Surface Area (TSA) of a cube?
The primary difference is which faces are included in the calculation:
- Lateral Surface Area (LSA) refers to the area of only the four vertical faces (the sides) of the cube. The formula is LSA = 4a². It excludes the top and bottom faces.
- Total Surface Area (TSA) includes the area of all six faces of the cube (the four sides plus the top and bottom). The formula is TSA = 6a².
3. How do the formulas for the perimeter of a cube and a cuboid differ?
The difference in formulas comes from the dimensions of the shapes. A cube has 12 edges of equal length ('a'), so its perimeter formula is simple: Perimeter = 12a. In contrast, a cuboid has edges of different lengths (length 'l', breadth 'b', height 'h'), so its perimeter is calculated by summing all its edges, leading to the formula: Perimeter = 4(l + b + h).
4. What is the formula for the volume of a cube?
The volume of a cube represents the three-dimensional space it occupies. It is calculated by multiplying the side length by itself three times. If the side of the cube is 'a', the formula is Volume (V) = a × a × a = a³. The result is always expressed in cubic units, such as cm³ or m³.
5. Why is the perimeter of a cube calculated as 12 times its side length?
A cube is a 3D solid with 6 square faces and 8 vertices (corners). These faces are connected by a total of 12 edges. A key property of a cube is that all its 12 edges are of equal length. The term 'perimeter' in this context refers to the total length of its wireframe structure. Therefore, to find the total length, you sum the lengths of all 12 identical edges, which simplifies to the formula 12 × a.
6. What is the real-world importance of calculating a cube's surface area?
Calculating a cube's surface area has several practical applications in everyday life. For instance:
- Manufacturing and Packaging: It helps determine the exact amount of material (like paper or cardboard) needed to create a cubical box without wastage.
- Construction and Decoration: It is used to calculate the amount of paint required to cover the walls of a cubical room or the number of tiles needed for its floor and walls.
- Heat Transfer in Science: In physics, the surface area is crucial for calculating the rate at which an object loses or gains heat from its surroundings.
7. How does doubling the side of a cube affect its perimeter, surface area, and volume?
Changing a cube's side length has a different level of impact on its various properties. If you double the side length from 'a' to '2a':
- The Perimeter (a one-dimensional measure) will double (12a becomes 24a).
- The Surface Area (a two-dimensional measure) will become four times larger (6a² becomes 6(2a)² = 24a²).
- The Volume (a three-dimensional measure) will become eight times larger (a³ becomes (2a)³ = 8a³).
8. Is the 'perimeter of a cube' the same as the perimeter of one of its faces?
No, they are two different concepts. The perimeter of a single face of a cube (which is a square) is the length of the boundary of that 2D shape, calculated as 4a. The perimeter of a cube is a term used for the total length of all 12 edges of the 3D shape, which is calculated as 12a. It is a common misconception to confuse these two measurements.









