Rules of Inequality: Explained with Examples

A mathematical expression with unequal sides is referred to as an inequality. An inequality in maths, in its simplest form, compares any two values and maintains that one value is less than, greater than, or not equal to the value on the other side of the equation. Two equal expressions are used when solving equations. As implied by the name, we explore inequalities when we evaluate two expressions that are "unequal" or disproportional to one another. The result is that one equation will have a larger value than the other. There are four basic types of inequality: less than, greater than, less than or equal to, and greater than or equal to.

Linear Inequality Definition

A mathematical expression that compares two values using the inequality symbols is known as linear inequalities. If no term involves the product of the variables and each variable's exponent is only of the first degree, an inequation is said to be linear. Inequalities can be defined as a statement involving a variable(s) and the sign of the inequality, $>,<, \leq, \geq$ or two real numbers or two algebraic expressions connected by the symbol $>,<, \leq, \geq$ form an inequality in maths.

Symbols Used in Inequalities

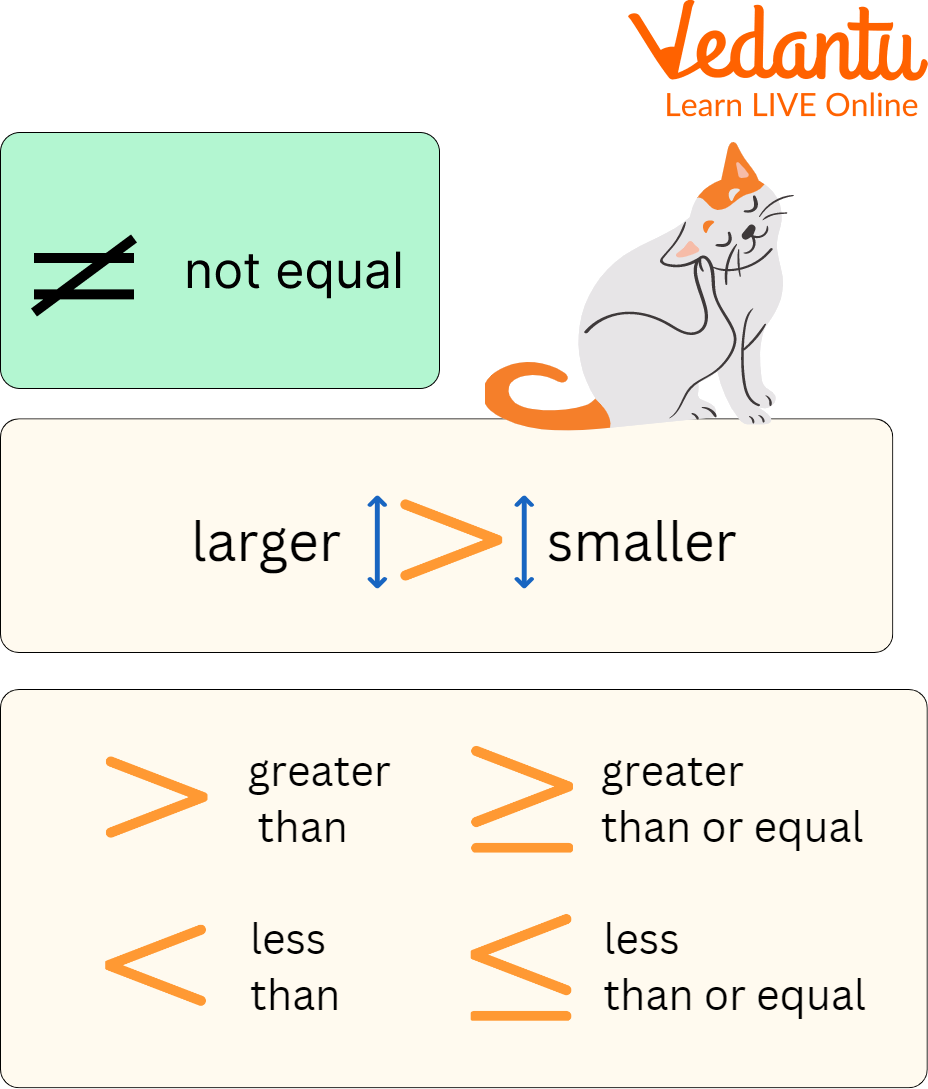
Symbols Used in Inequalities

1. Less than is denoted by the symbol $<$.

2. Greater than is denoted by the symbol $>$.

3. Less than or equal to is denoted by the symbol with a bar underneath it $\leq$.

4. Greater than or equal to is denoted by the symbol with a bar underneath it $\geq$.

5. The symbol usually indicates that the quantities on the left and right sides are not equal $ \neq $.

Rules of Inequalities

1. The inequality symbol remains unchanged when the same number is added to both sides of an inequality. For Example - if we have $a<b$, then $a+c<b+c$.

2. The inequality sign is unaffected by subtracting the same amount from both sides of the inequality. For Example - if we have $a>b$, then $a-c>b-c$.

3. The inequality sign is unaffected by multiplying both sides of an inequality by a positive number. For Example - if we have $a<b$ and if $c$ is a positive number, then $a \times c < b \times c$

4. An inequality's sign is unaffected by dividing both sides by a positive number. For Example - If $a<b$ and $c$ are positive numbers, then $\frac{a}{c}<\frac{b}{c}$.

5. Multiplying both sides of an inequality equation by the same negative number changes the direction of the inequality symbol. For Example - If we have $a<b$ and $c$ is a negative number, then $a\times c>b \times c$.

6. Dividing both sides of an inequality equation by a same negative number changes the direction of the inequality symbol. For Example - If we have a < b and if c is a negative number, then $\frac{a}{c}>\frac{b}{c}$.

Solved Examples

Example 1: Solve $2 x-6 \leq 3-x$.

Solution: Let's start solving the inequality by adding both sides by 6 we get;

$2 x-6+6 \leq 3+6-x$

$2 x \leq 9-x$

Add both sides by x

$2 x+x \leq 9-x+x$

$3 x \leq 9$

Now, we divide both sides of the inequality by 3;

$x \leq 3$

Example 2: Solve $x+4>5$.

Solution: Here, we have only one variable, so we can easily isolate the variable $x$ by subtracting 4 from both sides of the inequality we get;

$x+4-4>5-4$

$\Rightarrow x>1$

Hence, $x>1$

Example 3: Solve $5 x+20>3 x+24$

Solution: Let's start solving the inequality by subtracting 20 from both sides of the inequality we get;

$5 x+20-20>3 x+24-20$

$5 x>3 x+4$

Now we subtract both sides of the inequality by $3 x$.

$5x-3x>3x-3x+4$

$2x>4$

Dividing both sides by 2;

$x>2$

Practice Problems

Q 1. Solve $\frac{x}{4}>5$. (Ans: $x>20$)

Q 2. Solve $8 x-2>0$. (Ans: $x>\frac{1}{4}$)

Summary

This article summarises the definition of Linear inequalities in mathematics. We use four basic types of inequality symbols: less than, greater than, less than or equal to, and greater than or equal to. If there is no term involving the product of the variables and each variable's exponent is only of the first degree, an inequation is said to be linear inequality. There are some important rules for solving inequalities that are discussed in the articles with solved examples.