
Net positive charge on the inner spherical conductor is $3Q$ and on the outer spherical conductor is $Q$. Switch is closed.
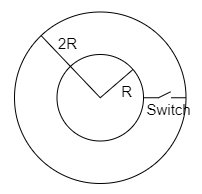
(A) charge will flow from inner shell to outer shell
(B) charge will flow from outer shell to inner shell
(C) charge will not flow
(D) none of these
Answer
139.8k+ views
Hint: Already we know that the charge will flow from high charge to the low charge. By determining the total charge of the system, and then equating the potential due to two shells are the same. Then the charge relation can be determined. And by using the total charge equation, the individual charge can be determined.
Useful formula
The electric potential is given by,
$V = \dfrac{Q}{R}$.
Where, $V$ is the electric potential, $Q$ is the charge and $R$ is the distance.
Complete step by step solution
Given that,
The charge of the outer shell is, $Q$,
The charge of the inner shell is $3Q$.
The total charge of the system is equal to the sum of the individual charges, $ \Rightarrow Q + 3Q = 4Q$.
The initial energy before the switch is closed on $2R$ is $Q$,
The initial energy before the switch is closed on $R$ is $3Q$.
After the switch is closed, then
Now by equating the electric potential of the two shells are same, then
${V_1} = {V_2}$
Where, ${V_1}$ is the electric potential of the outer shell and ${V_2}$ is the electric potential of the inner shell.
Then the above equation is written as,
$\dfrac{{{Q_1}}}{{2R}} = \dfrac{{{Q_2}}}{R}$
Where, ${Q_1}$ is the charge of the outer shell after the switch is closed and ${Q_2}$ is the charge of the inner shell after the switch is closed.
By cancelling the terms in the above equation, then
$\dfrac{{{Q_1}}}{2} = \dfrac{{{Q_2}}}{1}$
By rearranging the terms, then
${Q_1} = 2{Q_2}$
The total charge of the system is,
${Q_1} + {Q_2} = 4Q$
By substituting the value of the ${Q_1}$ in the above equation, then
$2{Q_2} + {Q_2} = 4Q$
By adding the terms, then
$3{Q_2} = 4Q$
By rearranging the terms, then
${Q_2} = \dfrac{4}{3}Q$
On dividing the terms, then
${Q_2} = 1.33Q$
Substituting the ${Q_2}$ value in the equation of \[{Q_1}\], then
${Q_1} = 2 \times 1.33Q$
On multiplying the terms, then
${Q_1} = 2.66Q$
By comparing the values of ${Q_1}$ and ${Q_2}$, the charge in ${Q_1}$ is higher.
So, the charge flows from the outer shell to the inner shell.
Hence, the option (B) is the correct answer.
Note: The charge flows from high charge to the low charge, so that the outer shell has the higher charge than the inner shell after the switch between the outer shell and the inner shell is closed. By adding the charge of the outer shell and the inner shell is equal to the total charge of the system.
Useful formula
The electric potential is given by,
$V = \dfrac{Q}{R}$.
Where, $V$ is the electric potential, $Q$ is the charge and $R$ is the distance.
Complete step by step solution
Given that,
The charge of the outer shell is, $Q$,
The charge of the inner shell is $3Q$.
The total charge of the system is equal to the sum of the individual charges, $ \Rightarrow Q + 3Q = 4Q$.
The initial energy before the switch is closed on $2R$ is $Q$,
The initial energy before the switch is closed on $R$ is $3Q$.
After the switch is closed, then
Now by equating the electric potential of the two shells are same, then
${V_1} = {V_2}$
Where, ${V_1}$ is the electric potential of the outer shell and ${V_2}$ is the electric potential of the inner shell.
Then the above equation is written as,
$\dfrac{{{Q_1}}}{{2R}} = \dfrac{{{Q_2}}}{R}$
Where, ${Q_1}$ is the charge of the outer shell after the switch is closed and ${Q_2}$ is the charge of the inner shell after the switch is closed.
By cancelling the terms in the above equation, then
$\dfrac{{{Q_1}}}{2} = \dfrac{{{Q_2}}}{1}$
By rearranging the terms, then
${Q_1} = 2{Q_2}$
The total charge of the system is,
${Q_1} + {Q_2} = 4Q$
By substituting the value of the ${Q_1}$ in the above equation, then
$2{Q_2} + {Q_2} = 4Q$
By adding the terms, then
$3{Q_2} = 4Q$
By rearranging the terms, then
${Q_2} = \dfrac{4}{3}Q$
On dividing the terms, then
${Q_2} = 1.33Q$
Substituting the ${Q_2}$ value in the equation of \[{Q_1}\], then
${Q_1} = 2 \times 1.33Q$
On multiplying the terms, then
${Q_1} = 2.66Q$
By comparing the values of ${Q_1}$ and ${Q_2}$, the charge in ${Q_1}$ is higher.
So, the charge flows from the outer shell to the inner shell.
Hence, the option (B) is the correct answer.
Note: The charge flows from high charge to the low charge, so that the outer shell has the higher charge than the inner shell after the switch between the outer shell and the inner shell is closed. By adding the charge of the outer shell and the inner shell is equal to the total charge of the system.
Recently Updated Pages
JEE Main Participating Colleges 2024 - A Complete List of Top Colleges

JEE Main Maths Paper Pattern 2025 – Marking, Sections & Tips

Sign up for JEE Main 2025 Live Classes - Vedantu

JEE Main 2025 Helpline Numbers - Center Contact, Phone Number, Address

JEE Main Course 2025 - Important Updates and Details

JEE Main 2025 Session 2 Form Correction (Closed) – What Can Be Edited

Trending doubts
JEE Main 2025 Session 2: Application Form (Out), Exam Dates (Released), Eligibility, & More

JEE Main 2025: Derivation of Equation of Trajectory in Physics

A point charge + 20mu C is at a distance 6cm directly class 12 physics JEE_Main

JEE Main Exam Marking Scheme: Detailed Breakdown of Marks and Negative Marking

Learn About Angle Of Deviation In Prism: JEE Main Physics 2025

Electric Field Due to Uniformly Charged Ring for JEE Main 2025 - Formula and Derivation

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

JEE Main 2025: Conversion of Galvanometer Into Ammeter And Voltmeter in Physics

Degree of Dissociation and Its Formula With Solved Example for JEE

Electric field due to uniformly charged sphere class 12 physics JEE_Main

Dual Nature of Radiation and Matter Class 12 Notes: CBSE Physics Chapter 11

Formula for number of images formed by two plane mirrors class 12 physics JEE_Main




