Physics Notes for Chapter 11 Dual Nature of Radiation and Matter Class 12 - FREE PDF Download



FAQs on Dual Nature of Radiation and Matter Class 12 Physics Chapter 11 CBSE Notes - 2025-26
1. What is the core idea behind the dual nature of radiation and matter as covered in Class 12 Physics revision notes?
The core idea is that both radiation (like light) and matter (like electrons) can exhibit both wave-like and particle-like properties. This concept bridges classical and quantum physics, helping explain phenomena such as the photoelectric effect and de Broglie’s hypothesis, which are key for understanding modern physics topics in the CBSE Class 12 syllabus.
2. How does the photoelectric effect demonstrate the particle nature of light?
The photoelectric effect shows that when light above a certain frequency strikes a metal surface, it can release electrons from the material. This process depends on the energy of individual photons, not the total intensity, supporting the idea that light behaves as particles called photons with quantized energy ($E = h\nu$).
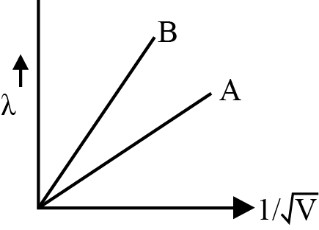
3. Why is de Broglie’s hypothesis significant when revising for Dual Nature of Radiation and Matter?
De Broglie’s hypothesis proposes that all matter, not just light, has an associated wavelength ($\lambda = \frac{h}{p}$). This is significant because it links particle and wave behavior, demonstrating that even electrons have wave-like properties—a cornerstone for understanding quantum mechanics, as emphasized in Class 12 revision notes.
4. Which formulas are essential for quick revision of this chapter, and what do they represent?
- Energy of a photon: $E = h\nu$ — calculates energy carried by light particles.
- Photoelectric equation: $E_k = h\nu - \phi$ — gives kinetic energy of emitted electrons in the photoelectric effect.
- de Broglie wavelength: $\lambda = \frac{h}{p}$ — relates wavelength and momentum of a particle.
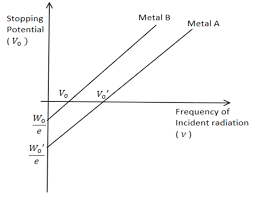
5. What is the work function, and why does it matter in understanding electron emission processes?
The work function is the minimum energy needed to release an electron from a metal surface. It is critical in determining whether incoming photons have enough energy to eject electrons and directly affects calculations in the photoelectric effect using the equation $E_k = h\nu - \phi$.
6. How can the wave-particle duality be observed in real-world experiments described in Class 12 revision notes?
Wave-particle duality is observed in experiments like the photoelectric effect (showing particle nature) and electron diffraction or interference (showing wave nature). These experiments confirm that both light and particles exhibit behaviors that cannot be explained by classical physics alone.
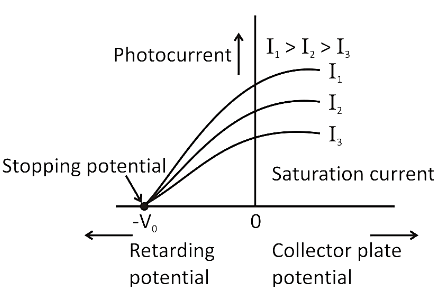
7. In the context of quick revision, how is the stopping potential related to the frequency of incident light?
As the frequency of incident light increases, the stopping potential required to halt photoelectrons also increases. This is because higher frequency photons have more energy, leading to more energetic ejected electrons, which require a greater potential to stop. The relation is given by $eV_s = h\nu - \phi$.
8. What is the importance of Planck’s constant in this chapter of Physics revision notes?
Planck’s constant (h) is a fundamental constant essential for quantifying energy in quantum processes. It appears in formulas for photon energy and de Broglie wavelength, connecting energy, frequency, and wavelength in all calculations throughout the chapter.
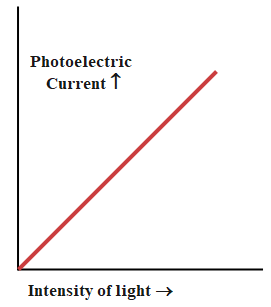
9. How does increasing the intensity of light affect photoelectric current in the chapter’s key experiments?
Increasing the intensity of light increases the number of photons hitting the metal, which leads to more electrons being ejected and therefore raises the photoelectric current. However, it does not affect the energy of the emitted electrons; only the frequency determines that.
10. What misconception should students avoid when revising the concept of the photoelectric effect?
A common misconception is that higher light intensity always increases the kinetic energy of emitted electrons. In reality, only frequency above the threshold increases kinetic energy; intensity only increases the number of emitted electrons (current), not their energy.
11. Why can’t we observe the wave nature of macroscopic objects like a football, according to the revision notes?
The de Broglie wavelength of macroscopic objects (like a football) is extremely small due to their large mass, making their wave properties practically unobservable. This contrasts with particles like electrons, where wave nature is significant and measurable.
12. How does the chapter’s concept map help in structuring exam revision for Dual Nature of Radiation and Matter?
A structured concept map connects all key topics—wave-particle duality, photoelectric effect, de Broglie hypothesis, experimental observations—helping you visualize how concepts are interlinked and ensuring thorough and efficient revision before exams.
13. What experimental evidence led to the acceptance of wave-particle duality in physics?
Experiments such as Hertz’s observation of the photoelectric effect and electron diffraction by Davisson and Germer provided compelling evidence. These showed light and electrons behaving as both particles and waves, leading to the acceptance of dual nature in modern physics.
14. In revision, how does understanding Heisenberg’s Uncertainty Principle deepen the study of dual nature?
Heisenberg’s Uncertainty Principle states that the position and momentum of a particle cannot both be precisely known at the same time. This highlights the quantum behavior of particles and further demonstrates the limitations of classical concepts when studying wave-particle duality.
15. What tips can help students efficiently revise the key points of Dual Nature of Radiation and Matter before exams?
- Focus on understanding the core concepts like wave-particle duality, not just memorizing formulas.
- Practice application-based and numerical problems frequently found in the CBSE board exam.
- Use short summaries and concept maps to quickly recall important topics.
- Connect theoretical principles to real-life experiments to solidify understanding.