Waves Optics Class 12 Extra Questions and Answers Free PDF Download



FAQs on CBSE Important Questions for Class 12 Physics Waves Optics - 2025-26
1. What are the most important topics to prepare in Wave Optics for the CBSE Class 12 board exams 2025-26?
For the 2025-26 CBSE Class 12 Physics exam, you should focus on these key areas in Wave Optics:
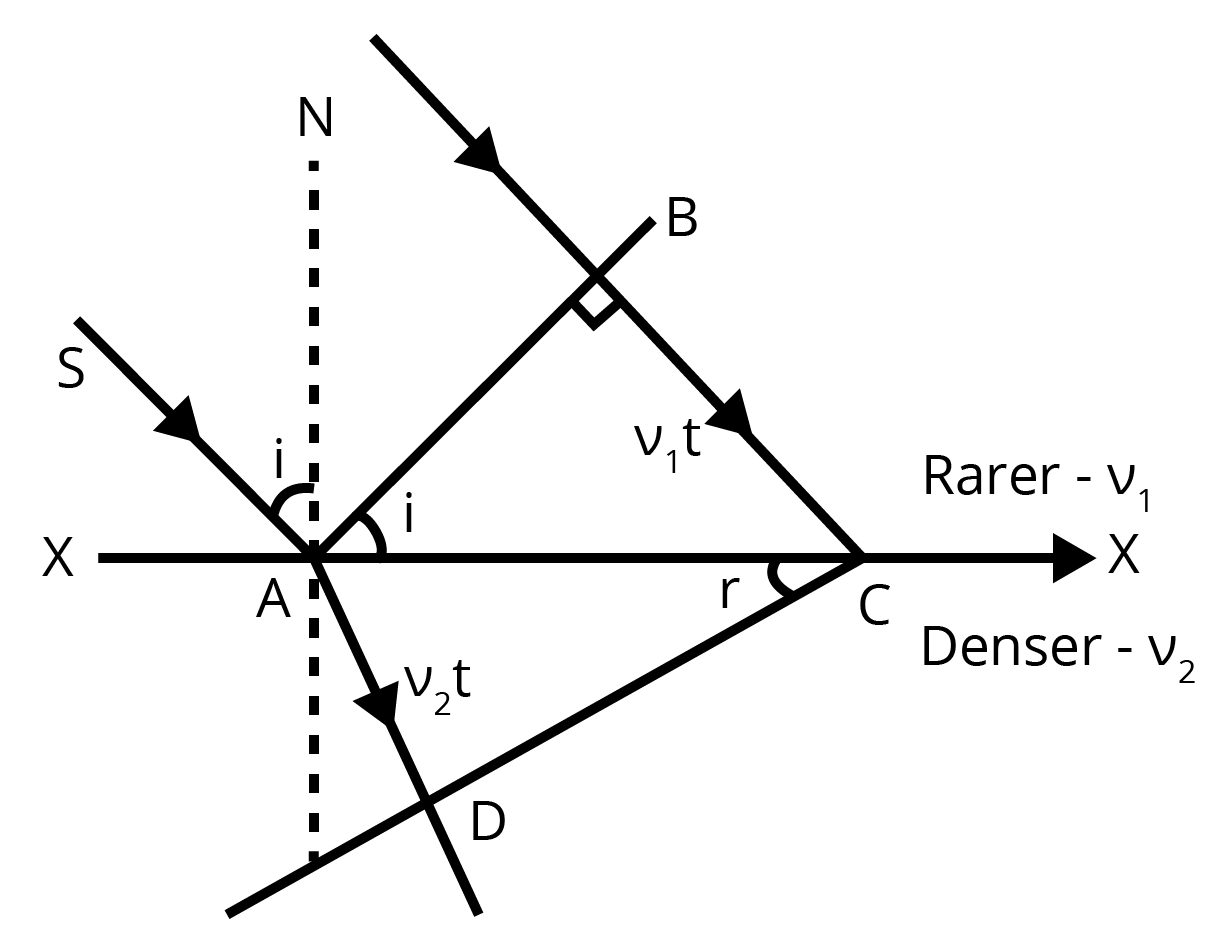
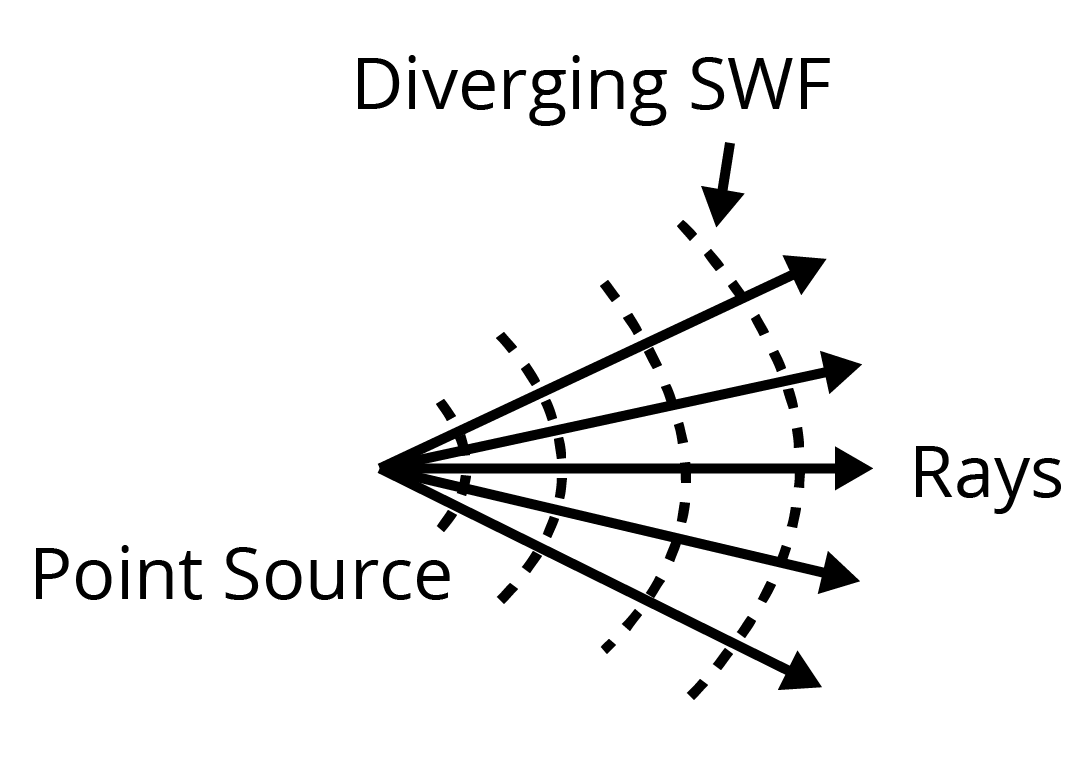
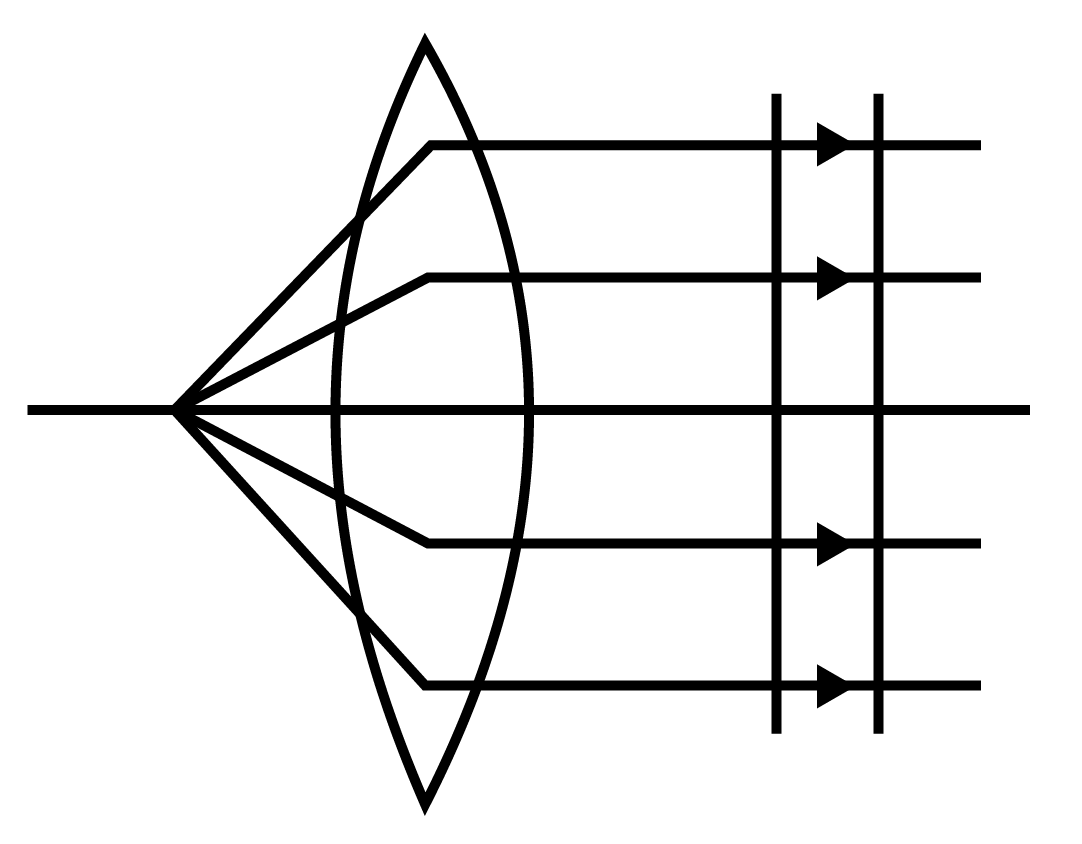
- Huygens' Principle: Understand the principle and its application to prove the laws of reflection and refraction of plane waves.
- Interference: Master Young's double-slit experiment (YDSE), including the derivation for fringe width, conditions for constructive and destructive interference, and related numerical problems.
- Coherent and Incoherent Sources: Understand the conditions required for sustained interference.
- Diffraction: Focus on diffraction due to a single slit, the width of the central maximum, and the conditions for minima and maxima.
- Polarisation: Learn about plane-polarised light, Brewster's law, and Malus's law.
2. What is the expected marks weightage for Chapter 10, Wave Optics, in the board exams?
In the CBSE Class 12 Physics paper, Wave Optics, combined with Ray Optics, forms the Optics unit, which typically carries a high weightage, often around 14-16 marks. For Wave Optics specifically, you can expect a mix of Very Short Answer (VSA), Short Answer (SA), and potentially a Long Answer (LA) question involving a key derivation or a detailed numerical problem.
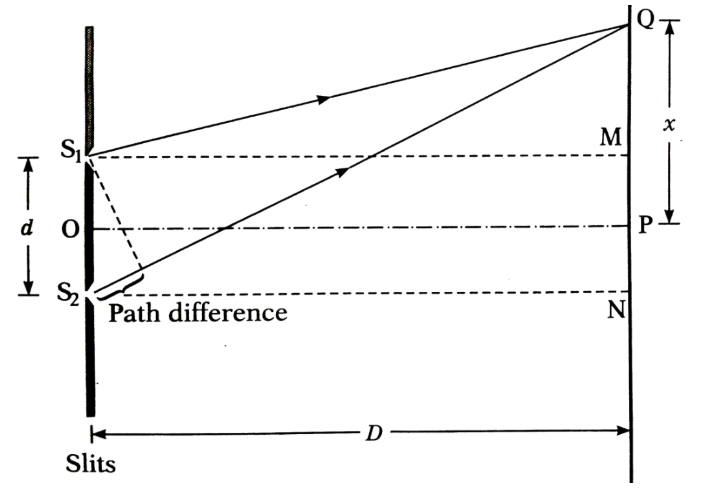
3. How is the expression for fringe width in Young's double-slit experiment (YDSE) derived?
The derivation involves finding the path difference (Δx) between waves from two coherent slits (S₁ and S₂) reaching a point P on a screen. Using the approximation that the screen distance D is much larger than the slit separation d (D >> d), the path difference is found to be Δx = yd/D. For bright fringes (constructive interference), the path difference must be an integral multiple of the wavelength (Δx = nλ). This gives the position of the n-th bright fringe as yₙ = nλD/d. The fringe width (β) is the separation between two consecutive bright fringes, calculated as β = yₙ₊₁ - yₙ. Therefore, β = λD/d.
4. Why are coherent sources necessary to observe a sustained interference pattern?
A sustained, or stable, interference pattern requires that the positions of maximum intensity (bright fringes) and minimum intensity (dark fringes) do not change over time. This is only possible if the phase difference between the two interfering waves remains constant at every point. Coherent sources are defined as sources that emit light waves of the same frequency and a constant phase difference, which is the essential condition to produce a stationary and observable interference pattern.
5. What is the fundamental difference between interference and diffraction?
The fundamental difference lies in their origin. Interference is the phenomenon resulting from the superposition of light waves coming from two or more different coherent sources. In contrast, diffraction is the result of the superposition of secondary wavelets originating from different points on the same single wavefront that has been obstructed or passed through a narrow aperture.
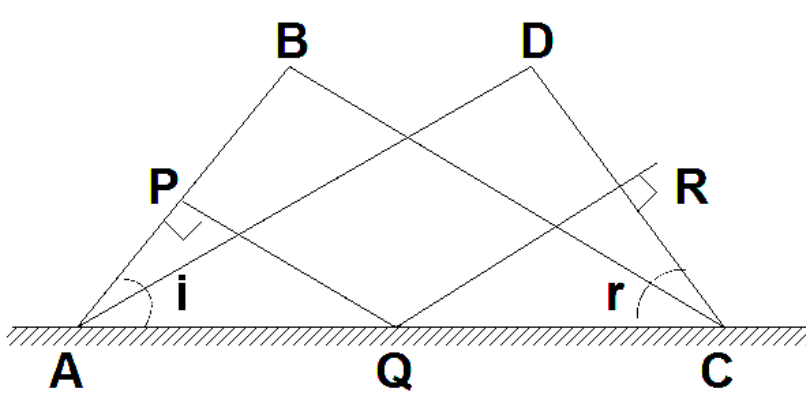
6. State Brewster's Law and prove that at the polarising angle, the reflected and refracted rays are perpendicular to each other.
Brewster's Law states that for a transparent medium, the tangent of the polarising angle of incidence (iₚ) is equal to its refractive index (μ). Mathematically, μ = tan(iₚ).
To prove that the rays are perpendicular at this angle:
- According to Snell's Law, μ = sin(iₚ) / sin(rₚ).
- According to Brewster's Law, μ = tan(iₚ) = sin(iₚ) / cos(iₚ).
- Equating these two expressions for μ, we get: sin(iₚ) / sin(rₚ) = sin(iₚ) / cos(iₚ).
- This simplifies to sin(rₚ) = cos(iₚ), which can be written as sin(rₚ) = sin(90° - iₚ).
- Therefore, rₚ = 90° - iₚ, which means iₚ + rₚ = 90°. This proves that the reflected and refracted rays are perpendicular to each other.
7. When a low-flying aircraft passes overhead, the picture on a TV screen sometimes shakes. Why does this happen?
This occurs due to the phenomenon of interference. The TV antenna receives two signals: the direct signal from the broadcasting tower and a second signal reflected from the metallic body of the aircraft. These two signals superpose. As the aircraft moves, the path length of the reflected signal changes continuously. This causes the path difference between the two signals to change, leading to rapidly alternating constructive and destructive interference, which results in the shaking or flickering of the TV picture.
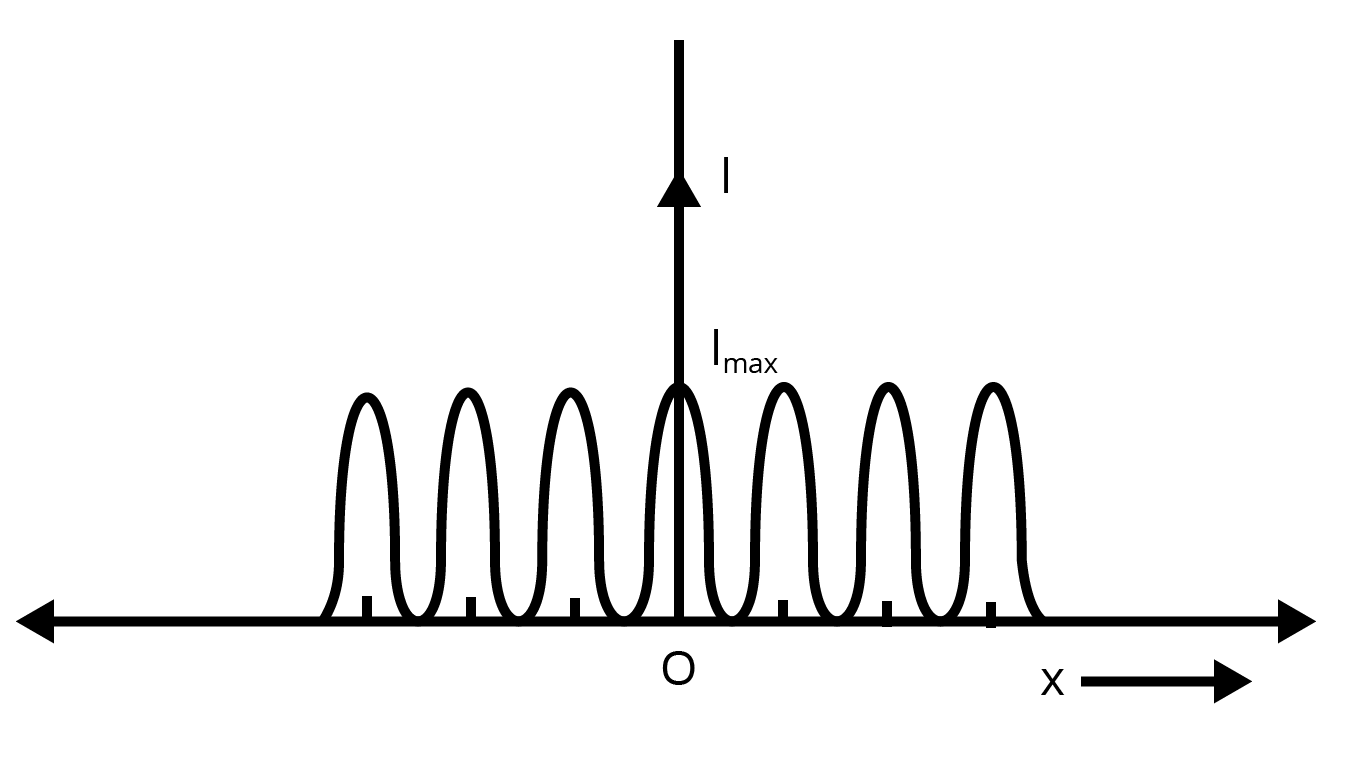
8. What happens to the diffraction pattern of a single slit if the monochromatic source is replaced by white light?
If white light is used instead of a monochromatic source, the diffraction pattern changes significantly. The central maximum will be white because all wavelengths interfere constructively at the centre. The secondary maxima on either side will be dispersed into a continuous spectrum of colours. For each secondary maximum, violet light will be closest to the centre and red light will be farthest, as the extent of diffraction is directly proportional to the wavelength (θ ≈ λ/a).
9. In a Young's double-slit experiment, the two slits have a width ratio of 4:1. What is the ratio of the intensity of maxima to minima in the interference pattern?
The intensity (I) is proportional to the square of the amplitude (a), and for small slits, amplitude is proportional to slit width (w). Therefore, I ∝ a² and a ∝ √w. Given the width ratio w₁/w₂ = 4/1, the ratio of amplitudes is a₁/a₂ = √4/√1 = 2/1. Let a₁ = 2k and a₂ = k.
The ratio of maximum to minimum intensity is given by: I_max / I_min = (a₁ + a₂)² / (a₁ - a₂)²
Substituting the values, we get: I_max / I_min = (2k + k)² / (2k - k)² = (3k)² / (k)² = 9k²/k² = 9/1.
Thus, the ratio is 9:1.
10. Why can two students in a room converse easily around a partition wall, but they cannot see each other?
This is explained by the difference in the diffraction of sound and light waves. For significant bending (diffraction) around an obstacle, the wavelength of the wave must be comparable to the size of the obstacle.
- Sound waves have relatively long wavelengths (in the order of metres), which are comparable to the size of the partition wall. Thus, they diffract easily around it, allowing the students to hear each other.
- Light waves have extremely small wavelengths (in the order of nanometres). This wavelength is negligible compared to the wall's size, so light travels in an almost straight line with minimal bending. As a result, the students cannot see each other.
11. How does wave theory explain the bright spot seen at the centre of the shadow of a tiny circular obstacle?
This phenomenon, known as the Arago spot or Poisson's spot, is a key proof of the wave nature of light. According to Huygens' principle, every point on the edge of the circular obstacle acts as a source of secondary wavelets. All the wavelets originating from the circumference of this obstacle travel the same distance to reach the exact centre of the shadow. Consequently, they all arrive at this central point in phase, leading to constructive interference and producing an unexpectedly bright spot.
12. In a single slit diffraction experiment, how does doubling the slit width affect the size and intensity of the central bright fringe?
In a single slit experiment, the angular width of the central maximum is given by the formula 2λ/a, where 'a' is the slit width.
- Size: If the slit width 'a' is doubled (a' = 2a), the new angular width becomes 2λ/(2a) = λ/a. This means the size of the central diffraction band is reduced to half its original size.
- Intensity: When the slit width is doubled, more light energy passes through it. Since this energy is now concentrated over a smaller area (half the width), the intensity of the central maximum increases significantly, becoming four times the original intensity.