Class 12 Maths Chapter 12 Summary Notes PDF Download



FAQs on Linear Programming Class 12 Maths Chapter 12 CBSE Notes - 2025-26
1. What are the key concepts students should focus on while revising Class 12 Linear Programming?
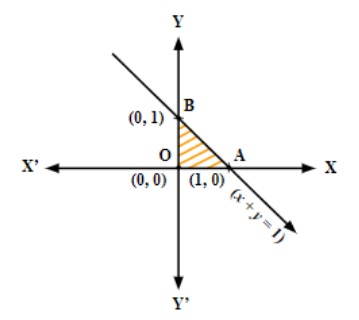
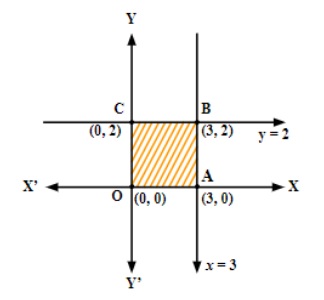
While revising Linear Programming, students should concentrate on core concepts such as the objective function, constraints, feasible region, graphical method (including the corner point method), and types of solutions like optimal, feasible, and infeasible solutions. Understanding these fundamentals is essential for both problem-solving and exam preparation.
2. How can you quickly summarize the structure of a standard Linear Programming Problem (LPP)?
A standard LPP consists of an objective function (to maximize or minimize), subject to linear constraints (inequalities or equations), and non-negativity restrictions for variables. Typically, it is stated as:
- Maximize or Minimize Z = c1x1 + c2x2 + ... + cnxn
- Subject to: a system of linear inequalities
- With x1, x2, ..., xn ≥ 0
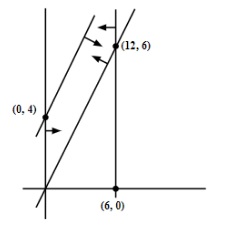
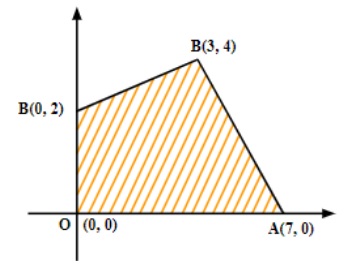
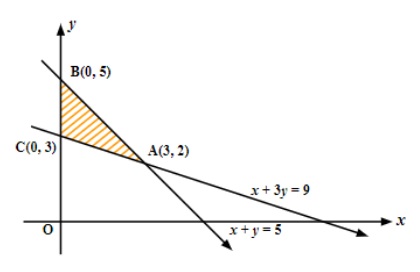
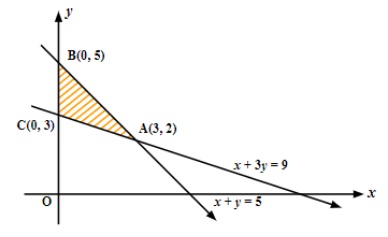
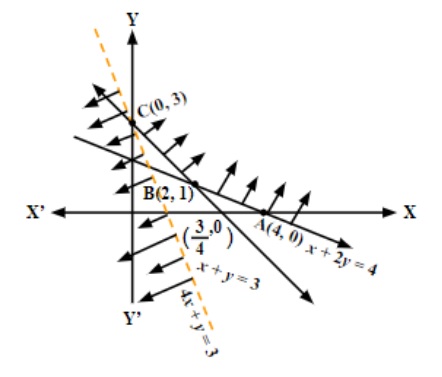
3. What is the most effective way to revise the graphical method for Linear Programming?
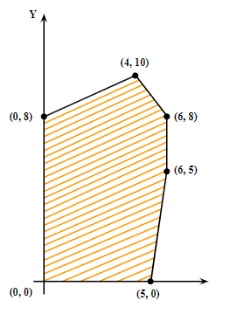
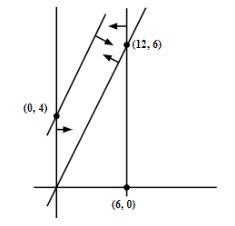
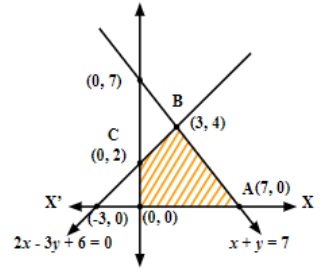
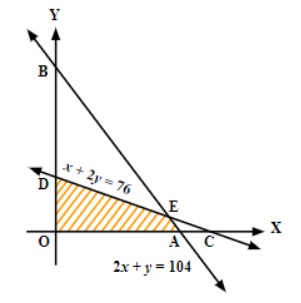
For quick revision, follow these steps:
- Plot each constraint as a straight line on the XY-plane.
- Identify the feasible region that satisfies all the constraints, including non-negativity.
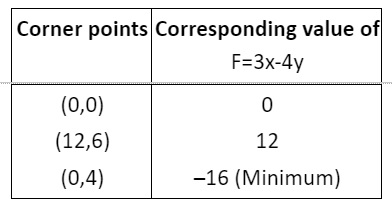
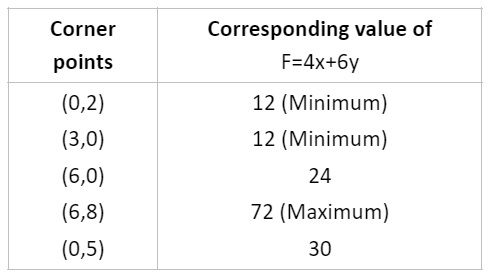
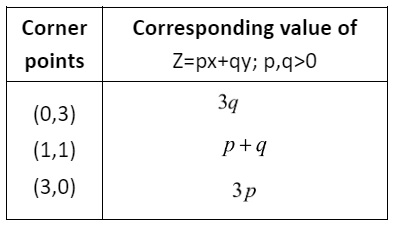
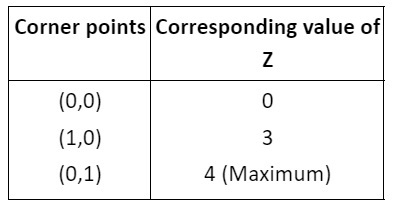
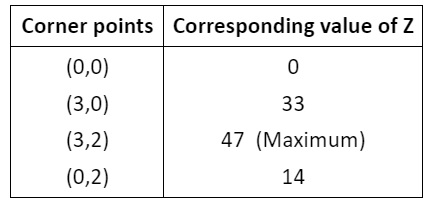
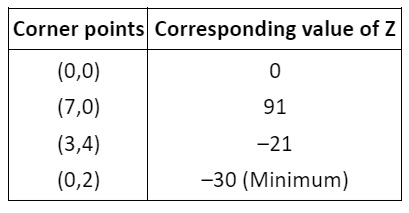
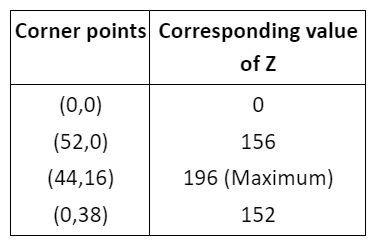
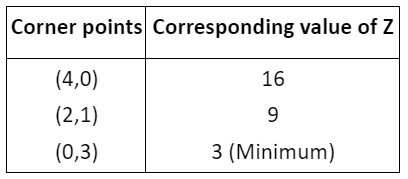
- Locate all corner points (vertices) of the feasible region.
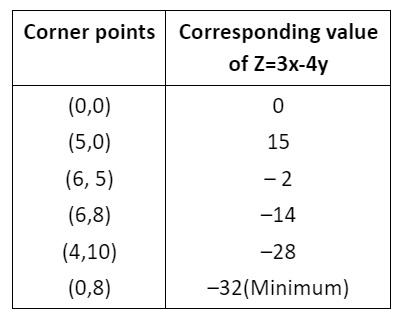
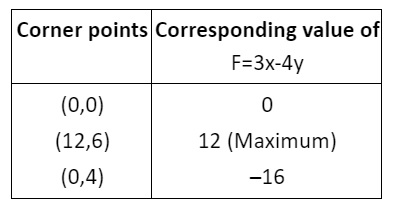
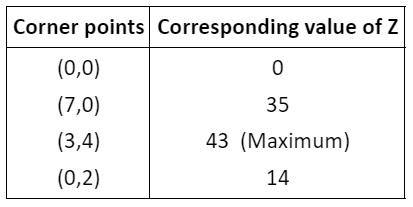
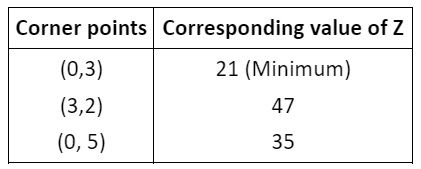
- Evaluate the objective function at each corner point.
- The maximum or minimum value of the objective function occurs at one of these corner points, as per the extreme point theorem.
4. What are the typical applications of Linear Programming covered in Class 12 revision notes?
Linear Programming is widely used for optimization in real-life situations, including:
- Production/Manufacturing problems: Determining the quantity of products to optimize profit or minimize costs given resources.
- Diet problems: Minimizing cost while meeting nutritional requirements.
- Transportation problems: Reducing transportation costs or time with given supply and demand.
5. Why is the feasible region always convex, and what is its significance in Linear Programming?
The feasible region formed by a set of linear constraints is always a convex polygon because the intersection of half-planes (from linear inequalities) yields a convex set. This is significant because the optimal solution (maximum or minimum) of the objective function, if it exists, always occurs at one of the vertices (corner points) of this convex region.
6. How do you quickly identify and avoid common mistakes when revising for Linear Programming?
Key pitfalls to avoid:
- Not applying non-negativity constraints, which may lead to invalid feasible regions.
- Failing to test corner points correctly when using the graphical method.
- Overlooking unbounded or infeasible solutions—always check if the feasible region is bounded.
- Confusing the objective function with a constraint.
7. What are some important points to remember for quick revision before the exam on Linear Programming?
Essential points to revise:
- Definition of objective function, constraints, and feasible region
- How to plot inequalities and find intersection points
- Role of slack and surplus variables in converting inequalities to equations
- Corner Point Method for finding optimal solution
- Applications and significance of bounded and unbounded feasible regions
8. How are Linear Programming concepts connected to real-world scenarios and other subjects?
Linear Programming has applications beyond mathematics, such as optimizing profit in business, maximizing outputs in manufacturing, and efficiently allocating resources in economics and management. Understanding LPP also enhances logical reasoning and problem-solving skills useful in subjects like Economics, Business Studies, and Computer Science.
9. What is the importance of assumptions in the formulation of Linear Programming Problems?
Assumptions in LPP formulation (such as linearity, finiteness, non-negativity, and certainty of data) are vital because they ensure the mathematical model can be solved accurately using linear methods. Deviations from these assumptions can make solutions invalid or infeasible, so it's critical to understand and verify them when revising.
10. How do you interconnect revision of Linear Programming with other chapters in Class 12 Maths?
Linear Programming directly uses concepts from Coordinate Geometry (plotting inequalities, finding intersections), Algebra (solving equations), and Graph Theory. A clear understanding of these foundational chapters helps in faster and more accurate solutions during revision and exams.