Vector Algebra Class 12 Maths Chapter 10 CBSE Notes - 2025-26

Vector:

Vector quantities are those quantities that have magnitude and direction. It is generally represented by a directed line segment. We represent a vector as \[\overrightarrow{\text{AB}}\], where initial point of vector is denoted by \[\text{A}\] and the terminal point by \[\text{B}\]. The magnitude of vector is expressed as \[\left| \overrightarrow{\text{AB}} \right|\].

Position Vector

Let us denote the origin as \[\text{O}\] such that this is a fixed point. There is a point, say \[\text{P}\] at a distance from \[\text{O}\]. Now, the position vector of a point \[\text{P}\] is given by the vector \[\overrightarrow{\text{OP}}\]. 

The next case is when there are two vectors, \[\overrightarrow{\text{a}}\] and \[\overrightarrow{\text{b}}\] which represent the position vectors of two points \[\text{A}\] and \[\text{B}\]. Then we can write the vector \[\overrightarrow{\text{AB}}\text{=}\overrightarrow{\text{b}}-\overrightarrow{\text{a}}\] or the position vector of \[\text{B}-\] the position vector of \[\text{A}\].

Types of Vectors

1. Zero Vector - It has zero magnitude. This means that vector has the same initial and terminal point. It is denoted by \[\overrightarrow{\text{O}}\]. The direction of zero vector is indeterminate.

2. Unit Vector - It has unit magnitude. Unit vector in direction of a vector \[\overrightarrow{\text{a}}\] is denoted by \[\widehat{\text{a}}\] and symbolically as \[\widehat{\text{a}}\text{=}\dfrac{\overrightarrow{\text{a}}}{\left| \overrightarrow{\text{a}} \right|}\].

3. Co-initial Vectors - Two or more vectors are said to be co-initial if they have the same initial point.

4. Equal Vectors - Two vectors are said to be equal if they have the same magnitude and direction. They represent the same physical quantity.

5. Collinear Vectors - Two or more vectors are said to be collinear if they are parallel to the same line irrespective of their direction. For this reason, they are also called parallel vectors. We have two sub-categories – like vectors (same direction) and unlike vectors (different directions). We can represent it mathematically by taking two non-zero vectors \[\overrightarrow{\text{a}}\] and \[\overrightarrow{\text{b}}\]. They are collinear if and only, if \[\overrightarrow{\text{a}}\text{=K}\overrightarrow{\text{b}}\], where \[\text{K}\in \text{R-}\left\{ \text{0} \right\}\].

6. Coplanar Vectors - Those vectors which lie on the same plane and they are all parallel to the same plane. We must remember that two vectors are always coplanar.

7. Negative Vector - A vector which has same magnitude but opposite direction to another vector is called negative of that vector.

Addition of Vectors

1. Triangle Law - Consider a triangle $ABC$. Let the sum of two vectors \[\overrightarrow{\text{a}}\text{ and }\overrightarrow{\text{b}}\] be represented by $\vec{c}$. The position vectors are represented by \[\overrightarrow{\text{AB}}\text{ , }\overrightarrow{\text{BC}}\text{ }and\text{ }\overrightarrow{\text{AC}}\].

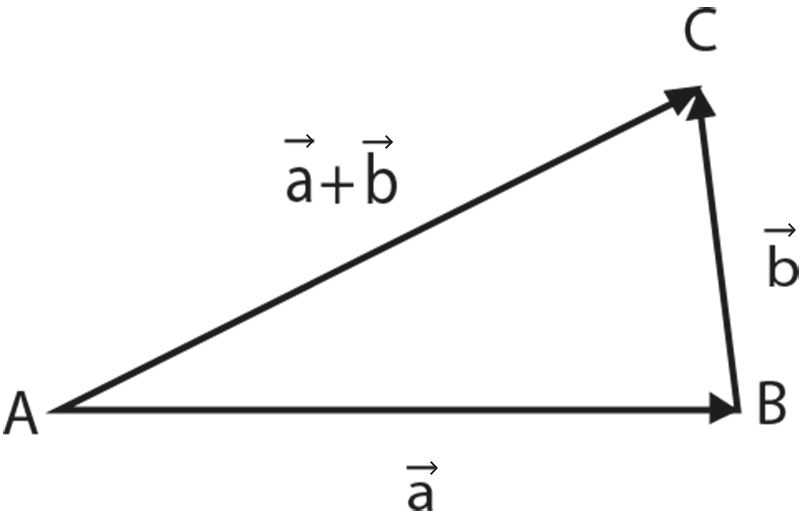
Triangle law of vector addition states that when two vectors are represented as two sides of the triangle with the order of magnitude and direction, then the third side of the triangle represents the magnitude and direction of the resultant vector.

So, we can write that $\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{BC}$.

2. Parallelogram Law - Consider a parallelogram $ABCD$. Let the sum of two vectors \[\overrightarrow{\text{a}}\text{ and }\overrightarrow{\text{b}}\] be represented by $\vec{c}$. The position vectors are represented as 

\[\vec{a}\text{ =}\overrightarrow{\text{AB}}\text{ = }\overrightarrow{\text{DC}}\]

\[\vec{b}\text{ =}\overrightarrow{\text{AD}}\text{ = }\overrightarrow{\text{BC}}\]

\[\vec{a}+\vec{b}\text{=}\overrightarrow{\text{AC}}\]

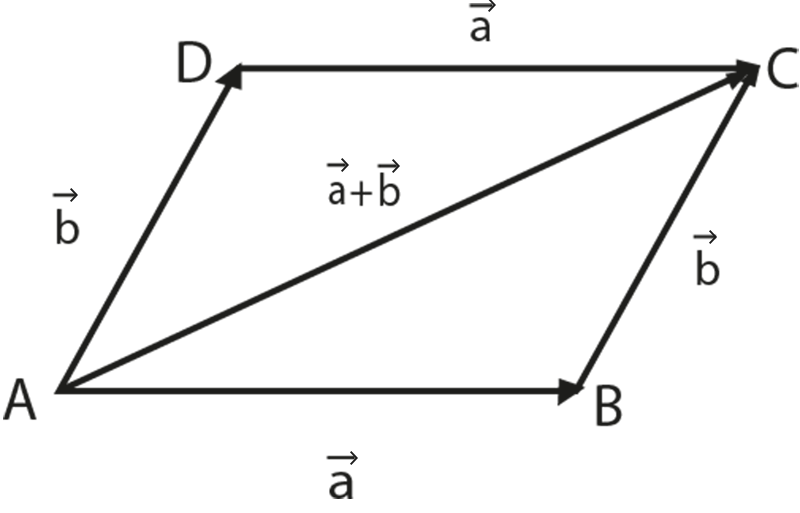
According to the parallelogram law of vector addition if two vectors act along two adjacent sides of a parallelogram (having magnitude equal to the length of the sides) both pointing away from the common vertex, then the resultant is represented by the diagonal of the parallelogram passing through the same common vertex and in the same sense as the two vectors.

The sum is

\[\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}\]

$\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}$

3. Properties of Vector Addition

1. Commutative property - \[\overrightarrow{\text{a}}\text{+}\overrightarrow{\text{b}}\text{=}\overrightarrow{\text{b}}\text{+}\overrightarrow{\text{a}}\]

2. Associative property - \[\left( \overrightarrow{\text{a}}\text{+}\overrightarrow{\text{b}} \right)\text{+}\overrightarrow{\text{c}}\text{=}\overrightarrow{\text{a}}\text{+}\left( \overrightarrow{\text{b}}\text{+}\overrightarrow{\text{c}} \right)\]

3. Zero is the additive identity - \[\overrightarrow{\text{a}}\text{+}\overrightarrow{\text{0}}\text{=}\overrightarrow{\text{a}}\text{=}\overrightarrow{\text{0}}\text{+}\overrightarrow{\text{a}}\] 

4. \[\overrightarrow{\text{a}}\text{+}\left( \text{-}\overrightarrow{\text{a}} \right)\text{=}\overrightarrow{\text{0}}\text{=}\left( \text{-}\overrightarrow{\text{a}} \right)\text{+}\overrightarrow{\text{a}}\] 

Multiplication of a Vector by a Scalar

If \[\overrightarrow{\text{a}}\] is a vector and \[\text{m}\] is a scalar, then their product is \[\text{m }\overrightarrow{\text{a}}\]. The magnitude would be \[\left| \text{m} \right|\] times the magnitude of \[\overrightarrow{\text{a}}\]. This is called scalar multiplication. If \[\overrightarrow{\text{a}}\] and \[\overrightarrow{\text{b}}\] are vectors and $m$ and $n$ are scalars, then

1. \[\text{m}\left( \overrightarrow{\text{a}} \right)\text{=}\left( \overrightarrow{\text{a}} \right)\text{m=m}\overrightarrow{\text{a}}\] 

2. \[\text{m}\left( \text{n}\overrightarrow{\text{a}} \right)\text{=n}\left( \text{m}\overrightarrow{\text{a}} \right)\text{=}\left( \text{mn} \right)\overrightarrow{\text{a}}\] 

3. \[\left( \text{m+n} \right)\overrightarrow{\text{a}}\text{=m}\overrightarrow{\text{a}}\text{+n}\overrightarrow{\text{a}}\]

4. \[\text{m}\left( \overrightarrow{\text{a}}\text{+}\overrightarrow{\text{b}} \right)\text{=m}\overrightarrow{\text{a}}\text{+m}\overrightarrow{\text{b}}\] 

Component Form of Vectors

• We have to consider three axis - $x,y,z$ and a point in the coordinate axis. So, the position vector for such a point would be written as $\overrightarrow{OP}=x\hat{i}+y\hat{j}+z\hat{k}$. This is the component form of vector.

• The scalar components are $x,y,z$ and the vector components are \[x\hat{i},y\hat{j},z\hat{k}\].

• Consider two vectors as \[\vec{A}=a\hat{i}+b\hat{j}+c\hat{k}\] and $\vec{B}=p\hat{i}+q\hat{j}+r\hat{k}$, then

1. Sum is given by $\vec{A}+\vec{B}=(a+p)\hat{i}+(b+q)\hat{j}+(c+r)\hat{k}$.

2. Difference is given by $\vec{A}-\vec{B}=(a-p)\hat{i}+(b-q)\hat{j}+(c-r)\hat{k}$.

3. Multiplication by a scalar $m$ is given by $m\vec{A}=ma\hat{i}+mb\hat{j}+mc\hat{k}$.

4. The vectors are equal if \[a=p,b=q,c=r\].

Test for Collinearity

Three points \[\text{A,B,C}\] with position vectors \[\overrightarrow{\text{a}}\text{,}\overrightarrow{\text{b}}\text{,}\overrightarrow{\text{c}}\] respectively are collinear, if and only if there exist scalar \[\text{x,y,z}\] not all zero simultaneously such that; \[\text{x}\overrightarrow{\text{a}}\text{+y}\overrightarrow{\text{b}}\text{+z}\overrightarrow{\text{c}}\text{=0}\], where \[\text{x+y+z=0}\].

Test for Coplanar Points

Four points \[\text{A,B,C,D}\] with position vectors \[\overrightarrow{\text{a}}\text{,}\overrightarrow{\text{b}}\text{,}\overrightarrow{\text{c}}\text{,}\overrightarrow{\text{d}}\] respectively are coplanar if and only if there exist scalars \[\text{x,y,z,w}\] not all zero simultaneously such that; \[\text{x}\overrightarrow{\text{a}}\text{+y}\overrightarrow{\text{b}}\text{+z}\overrightarrow{\text{c}}\text{+w}\overrightarrow{\text{d}}\text{=0}\], where \[\text{x+y+z+w=0}\].

Section Formula

1. Let \[\overrightarrow{\text{a}}\] and \[\overrightarrow{\text{b}}\] be the position vectors of two points \[\text{A}\] and \[\text{B}\]. A point $R$ with position vector as $\vec{r}$ divides $\overrightarrow{AB}$ such that $m\overrightarrow{RB}=n\overrightarrow{AR}$ and this denotes that $\overrightarrow{AB}$ is divided internally in the ratio \[\text{m:n}\] is given by \[\overrightarrow{\text{r}}\text{=}\dfrac{\text{m}\overrightarrow{\text{b}}+n\overrightarrow{\text{a}}}{\text{m+n}}\].

2. Let \[\overrightarrow{\text{a}}\] and \[\overrightarrow{\text{b}}\] be the position vectors of two points \[\text{A}\] and \[\text{B}\]. A point $R$ with position vector as $\vec{r}$ divides $\overrightarrow{AB}$ such that $m\overrightarrow{RB}=n\overrightarrow{AR}$ and this denotes that $\overrightarrow{AB}$ is divided externally in the ratio \[\text{m:n}\] is given by \[\overrightarrow{\text{r}}\text{=}\dfrac{\text{m}\overrightarrow{\text{b}}-n\overrightarrow{\text{a}}}{m-n}\].

3. Now if the ratio is $1:1$, then we can obtain the position vector of the midpoint as \[\dfrac{\overrightarrow{\text{a}}\text{+}\overrightarrow{\text{b}}}{\text{2}}\].

Magnitude of Vector

1. For a vector \[\vec{A}=a\hat{i}+b\hat{j}+c\hat{k}\], magnitude is $\left| A \right|=\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}$.

2. For vector $\overrightarrow{AB}$ with \[\vec{A}=a\hat{i}+b\hat{j}+c\hat{k}\] and $\vec{B}=p\hat{i}+q\hat{j}+r\hat{k}$, the magnitude is $\left| \overrightarrow{AB} \right|=\sqrt{{{(p-a)}^{2}}+{{(q-b)}^{2}}+{{(r-c)}^{2}}}$.

Product of Vectors

1. Scalar Product

• It is also called dot product. For two vectors \[\overrightarrow{\text{a}}\] and \[\overrightarrow{\text{b}}\], the dot product can be represented as \[\vec{a}.\vec{b}\] and it is defined as \[\overrightarrow{\text{a}}\cdot \overrightarrow{\text{b}}\text{=}\left| \overrightarrow{\text{a}} \right|\left| \overrightarrow{\text{b}} \right|\text{cos }\!\!\theta\!\!\text{ ;(0}\le \text{ }\!\!\theta\!\!\text{ }\le \text{ }\!\!\pi\!\!\text{ )}\].

• From this, we can find the angle between vectors as $\cos \theta =\dfrac{\vec{a}.\vec{b}}{\left| {\vec{a}} \right|\left| {\vec{b}} \right|}$.

• We have the below possibilities:

1. If \[\text{ }\!\!\theta\!\!\text{ }\] is acute, then \[\overrightarrow{\text{a}}\cdot \overrightarrow{\text{b}}\text{0}\].

2. If \[\text{ }\!\!\theta\!\!\text{ }\] is obtuse, then \[\overrightarrow{\text{a}}\cdot \overrightarrow{\text{b}}\text{0}\].

3. If \[\text{ }\!\!\theta\!\!\text{ }\] is zero, then \[\overrightarrow{\text{a}}\cdot \overrightarrow{\text{b}}=\left| {\vec{a}} \right|\left| {\vec{b}} \right|\].

4. If \[\text{ }\!\!\theta\!\!\text{ }\] is $\pi $, then \[\overrightarrow{\text{a}}\cdot \overrightarrow{\text{b}}=-\left| {\vec{a}} \right|\left| {\vec{b}} \right|\].

• If vectors \[\overrightarrow{\text{a}}\] and \[\overrightarrow{\text{b}}\] are non-zero and \[\vec{a}.\vec{b}=0\], then it is the condition for them to be perpendicular vectors.

• Considering component form and above point, we get results as

1. \[\widehat{\text{i}}\cdot \widehat{\text{i}}\text{=}\widehat{\text{j}}\cdot \widehat{\text{j}}\text{=}\widehat{\text{k}}\cdot \widehat{\text{k}}\text{=1}\]

2. \[\widehat{\text{i}}\cdot \widehat{\text{j}}\text{=}\widehat{\text{j}}\cdot \widehat{\text{k}}\text{=}\widehat{\text{k}}\cdot \widehat{\text{i}}\text{=0}\]

• If \[\overrightarrow{\text{a}}\text{=}{{\text{a}}_{\text{1}}}\widehat{\text{i}}\text{+}{{\text{a}}_{\text{2}}}\widehat{\text{j}}\text{+}{{\text{a}}_{\text{3}}}\widehat{\text{k}}\] and \[\overrightarrow{\text{b}}\text{=}{{\text{b}}_{\text{1}}}\widehat{\text{i}}\text{+}{{\text{b}}_{\text{2}}}\widehat{\text{j}}\text{+}{{\text{b}}_{\text{3}}}\widehat{\text{k}}\] then \[\overrightarrow{\text{a}}\cdot \overrightarrow{\text{b}}\text{=}{{\text{a}}_{1}}{{\text{b}}_{1}}+{{\text{a}}_{2}}{{\text{b}}_{2}}+{{\text{a}}_{3}}{{\text{b}}_{3}}\].

• Properties of Scalar Product

1. \[\overrightarrow{\text{a}}\cdot \overrightarrow{\text{a}}\text{=}{{\left| \overrightarrow{\text{a}} \right|}^{\text{2}}}\text{=}{{\overrightarrow{\text{a}}}^{\text{2}}}\text{,}\overrightarrow{\text{a}}\cdot \overrightarrow{\text{b}}\text{=}\overrightarrow{\text{b}}\cdot \overrightarrow{\text{a}}\] (Commutative) 

2. \[\overrightarrow{\text{a}}\cdot \left( \overrightarrow{\text{b}}\text{+}\overrightarrow{\text{c}} \right)\text{=}\overrightarrow{\text{a}}\cdot \overrightarrow{\text{b}}\text{+}\overrightarrow{\text{a}}\cdot \overrightarrow{\text{c}}\] (Distributive)

3. \[\left( \text{m}\overrightarrow{\text{a}} \right)\cdot \overrightarrow{\text{b}}\text{=}\overrightarrow{\text{a}}\cdot \left( \text{m}\overrightarrow{\text{b}} \right)\text{=m}\left( \overrightarrow{\text{a}}\cdot \overrightarrow{\text{b}} \right)\] (Associative), where \[\text{m}\] is scalar.

• Projection of vector \[\overrightarrow{\text{a}}\] on \[\overrightarrow{\text{b}}\text{=}\dfrac{\overrightarrow{\text{a}}\cdot \overrightarrow{\text{b}}}{\left| \overrightarrow{\text{b}} \right|}\].

• Maximum value of \[\overrightarrow{\text{a}}\cdot \overrightarrow{\text{b}}\text{=}\left| \overrightarrow{\text{a}} \right|\left| \overrightarrow{\text{b}} \right|\]

• Minimum value of  \[\overrightarrow{\text{a}}\cdot \overrightarrow{\text{b}}\text{=-}\left| \overrightarrow{\text{a}} \right|\left| \overrightarrow{\text{b}} \right|\]

• A vector in the direction of the bisector of the angle between two vectors \[\overrightarrow{\text{a}}\] and \[\overrightarrow{\text{b}}\] is \[\dfrac{\overrightarrow{\text{a}}}{\left| \overrightarrow{\text{a}} \right|}+\dfrac{\overrightarrow{\text{b}}}{\left| \overrightarrow{\text{b}} \right|}\].

• Hence bisector of the angle between the two vectors \[\overrightarrow{\text{a}}\] and \[\overrightarrow{\text{b}}\] is \[\text{ }\!\!\lambda\!\!\text{ }\left( \widehat{\text{a}}+\widehat{\text{b}} \right)\], where \[\text{ }\!\!\lambda\!\!\text{ }\in {{\text{R}}^{+}}\].

• Bisector of the exterior angle between \[\overrightarrow{\text{a}}\] and \[\overrightarrow{\text{b}}\] is \[\text{ }\!\!\lambda\!\!\text{ }\left( \widehat{\text{a}}\text{-}\widehat{\text{b}} \right)\text{ }\!\!\lambda\!\!\text{ }\in \text{R-}\left\{ \text{0} \right\}\].

2. Vector Product

• It is also called cross product. For two vectors \[\overrightarrow{\text{a}}\] and \[\overrightarrow{\text{b}}\], the vector product is represented as $\vec{a}\times \vec{b}$ and is defined by \[\overrightarrow{\text{a}}\text{ }\!\!\times\!\!\text{ }\overrightarrow{\text{b}}\text{=}\left| \overrightarrow{\text{a}} \right|\left| \overrightarrow{\text{b}} \right|\text{sin }\!\!\theta\!\!\text{ }\widehat{\text{n}}\], where $\theta $ is the angle between them and \[\widehat{\text{n}}\] is the unit vector perpendicular to both \[\overrightarrow{\text{a}}\] and \[\overrightarrow{\text{b}}\] such that \[\overrightarrow{\text{a}}\], \[\overrightarrow{\text{b}}\] and \[\widehat{\text{n}}\] form a right handed screw system.

• From this, we can write the angle between vectors as $\sin \theta =\dfrac{\left| \vec{a}\times \vec{b} \right|}{\left| {\vec{a}} \right|\left| {\vec{b}} \right|}$.

• If vectors \[\overrightarrow{\text{a}}\] and \[\overrightarrow{\text{b}}\] are non-zero and \[\vec{a}\times \vec{b}=0\], then it is the condition for them to be parallel vectors.

• Considering component form and above point, we get results as

1. \[\widehat{\text{i}}\text{ }\!\!\times\!\!\text{ }\widehat{\text{i}}\text{=}\widehat{\text{j}}\text{ }\!\!\times\!\!\text{ }\widehat{\text{j}}\text{=}\widehat{\text{k}}\text{ }\!\!\times\!\!\text{ }\widehat{\text{k}}\text{=0}\]

2. \[\widehat{\text{i}}\text{ }\!\!\times\!\!\text{ }\widehat{\text{j}}\text{=}\widehat{\text{k}}\text{,}\widehat{\text{j}}\text{ }\!\!\times\!\!\text{ }\widehat{\text{k}}\text{=}\widehat{\text{i}}\text{,}\widehat{\text{k}}\text{ }\!\!\times\!\!\text{ }\widehat{\text{i}}\text{=}\widehat{\text{j}}\]

• If \[\overrightarrow{\text{a}}\text{=}{{\text{a}}_{\text{1}}}\widehat{\text{i}}\text{+}{{\text{a}}_{\text{2}}}\widehat{\text{j}}\text{+}{{\text{a}}_{\text{3}}}\widehat{\text{k}}\] and \[\overrightarrow{\text{b}}\text{=}{{\text{b}}_{\text{1}}}\widehat{\text{i}}\text{+}{{\text{b}}_{\text{2}}}\widehat{\text{j}}\text{+}{{\text{b}}_{\text{3}}}\widehat{\text{k}}\] then 

\[\overrightarrow{\text{a}}\text{ }\!\!\times\!\!\text{ }\overrightarrow{\text{b}}\text{=}\left| \begin{matrix} \widehat{\text{i}} & \widehat{\text{j}} & \widehat{\text{k}}  \\   {{\text{a}}_{\text{1}}} & {{\text{a}}_{\text{2}}} & \text{a}  \\   {{\text{b}}_{\text{1}}} & {{\text{b}}_{\text{2}}} & \text{b}  \\ \end{matrix} \right|\].

• Geometrically, we can define \[\left| \overrightarrow{\text{a}}\text{ }\!\!\times\!\!\text{ }\overrightarrow{\text{b}} \right|\text{=}\] area of the parallelogram whose two adjacent sides are represented by \[\overrightarrow{\text{a}}\] and \[\overrightarrow{\text{b}}\].

• Properties of Vector Product

1. \[\overrightarrow{\text{a}}\text{ }\!\!\times\!\!\text{ }\overrightarrow{\text{b}}\ne \overrightarrow{\text{b}}\text{ }\!\!\times\!\!\text{ }\overrightarrow{\text{a}}\] (Not Commutative)

2. \[\left( \text{m}\overrightarrow{\text{a}} \right)\text{ }\!\!\times\!\!\text{ }\overrightarrow{\text{b}}\text{=}\overrightarrow{\text{a}}\text{ }\!\!\times\!\!\text{ }\left( \text{m}\overrightarrow{\text{b}} \right)\text{=m}\left( \overrightarrow{\text{a}}\text{ }\!\!\times\!\!\text{ }\overrightarrow{\text{b}} \right)\] (Associative) where \[\text{m}\] is scalar.

3. \[\overrightarrow{\text{a}}\text{ }\!\!\times\!\!\text{ }\left( \overrightarrow{\text{b}}\text{+}\overrightarrow{\text{c}} \right)\text{=}\left( \overrightarrow{\text{a}}\text{ }\!\!\times\!\!\text{ }\overrightarrow{\text{b}} \right)\text{+}\left( \overrightarrow{\text{a}}\text{ }\!\!\times\!\!\text{ }\overrightarrow{\text{c}} \right)\] (Distributive)

• Unit vector perpendicular to the plane of \[\overrightarrow{\text{a}}\] and \[\overrightarrow{\text{b}}\] is \[\widehat{\text{n}}\text{= }\!\!\pm\!\!\text{ }\dfrac{\overrightarrow{\text{a}}\text{ }\!\!\times\!\!\text{ }\overrightarrow{\text{b}}}{\left| \overrightarrow{\text{a}}\text{ }\!\!\times\!\!\text{ }\overrightarrow{\text{b}} \right|}\]

• A vector of magnitude \[\text{ }\!\!'\!\!\text{ r }\!\!'\!\!\text{ }\] and perpendicular to the plane of \[\overrightarrow{\text{a}}\text{ and }\overrightarrow{\text{b}}\] is  \[\text{ }\!\!\pm\!\!\text{ }\dfrac{\text{r}\left( \overrightarrow{\text{a}}\text{ }\!\!\times\!\!\text{ }\overrightarrow{\text{b}} \right)}{\left| \overrightarrow{\text{a}}\text{ }\!\!\times\!\!\text{ }\overrightarrow{\text{b}} \right|}\]

• If \[\overrightarrow{\text{a}}\text{,}\overrightarrow{\text{b}}\text{ and }\overrightarrow{\text{c}}\] are the position vectors of vertices \[\text{A,B and C}\] of a triangle, then the vector area of triangle is given by \[\text{ABC=}\dfrac{\text{1}}{\text{2}}\left[ \overrightarrow{\text{a}}\text{ }\!\!\times\!\!\text{ }\overrightarrow{\text{b}}+\overrightarrow{\text{b}}\text{ }\!\!\times\!\!\text{ }\overrightarrow{\text{c}}+\overrightarrow{\text{c}}\text{ }\!\!\times\!\!\text{ }\overrightarrow{\text{a}} \right]\] The points \[\text{A,B and C}\] are collinear if \[\overrightarrow{\text{a}}\text{ }\!\!\times\!\!\text{ }\overrightarrow{\text{b}}\text{+}\overrightarrow{\text{b}}\text{ }\!\!\times\!\!\text{ }\overrightarrow{\text{c}}\text{+}\overrightarrow{\text{c}}\text{ }\!\!\times\!\!\text{ }\overrightarrow{\text{a}}\text{=0}\].

• Area of quadrilateral whose diagonal vectors are \[\overrightarrow{{{\text{d}}_{1}}}\text{ and }\overrightarrow{{{\text{d}}_{2}}}\] is given by \[\dfrac{1}{2}\left| \overrightarrow{{{\text{d}}_{1}}}\times \overrightarrow{{{\text{d}}_{2}}} \right|\].

Scalar Triple Product

• The scalar triple product of three vectors \[\overrightarrow{\text{a}}\text{,}\overrightarrow{\text{b}}\text{ and }\overrightarrow{\text{c}}\] is defined as \[\overrightarrow{\text{a}}.\left( \overrightarrow{\text{b}}\times \overrightarrow{\text{c}} \right)\] and can be represented as \[\left[ \overrightarrow{\text{a}}\text{ }\overrightarrow{\text{b}}\text{ }\overrightarrow{\text{c}} \right]\]. It is also referred to as box product.

• Geometrically, it represents the volume of the parallelepiped whose three coterminous edges are represented by \[\overrightarrow{\text{a}}\text{,}\overrightarrow{\text{b}}\text{ and }\overrightarrow{\text{c}}\] . So \[\text{V=}\left[ \overrightarrow{\text{a}}\text{ }\overrightarrow{\text{b}}\text{ }\overrightarrow{\text{c}} \right]\].

• Scalar triple product is cyclic, i.e. the order of vectors can be interchanged in a cyclic manner as shown below, \[\overrightarrow{\text{a}}\cdot \left( \overrightarrow{\text{b}}\times \overrightarrow{\text{c}} \right)=\left( \overrightarrow{\text{a}}\times \overrightarrow{\text{b}} \right)\cdot \overrightarrow{\text{c}}\] or \[\left[ \overrightarrow{\text{a}}\text{ }\overrightarrow{\text{b}}\text{ }\overrightarrow{\text{c}} \right]=\left[ \overrightarrow{\text{b}}\text{ }\overrightarrow{\text{c}}\text{ }\overrightarrow{\text{a}} \right]=\left[ \overrightarrow{\text{c}}\text{ }\overrightarrow{\text{a}}\text{ }\overrightarrow{\text{b}} \right]\] \[\overrightarrow{\text{a}}\cdot \left( \overrightarrow{\text{b}}\times \overrightarrow{\text{c}} \right)=\text{-}\overrightarrow{\text{a}}\cdot \left( \overrightarrow{\text{c}}\times \overrightarrow{\text{b}} \right)\] or \[\left[ \overrightarrow{\text{a}}\text{ }\overrightarrow{\text{b}}\text{ }\overrightarrow{\text{c}} \right]=\text{-}\left[ \overrightarrow{\text{a}}\text{ }\overrightarrow{\text{c}}\text{ }\overrightarrow{\text{b}} \right]\]

• If \[\overrightarrow{\text{a}}\text{=}{{\text{a}}_{\text{1}}}\widehat{\text{i}}\text{+}{{\text{a}}_{\text{2}}}\widehat{\text{j}}\text{+}{{\text{a}}_{\text{3}}}\widehat{\text{k}}\]; \[\overrightarrow{\text{b}}\text{=}{{\text{b}}_{\text{1}}}\widehat{\text{i}}\text{+}{{\text{b}}_{\text{2}}}\widehat{\text{j}}\text{+}{{\text{b}}_{\text{3}}}\widehat{\text{k}}\] and \[\overrightarrow{\text{c}}\text{=}{{\text{c}}_{\text{1}}}\widehat{\text{i}}\text{+}{{\text{c}}_{\text{2}}}\widehat{\text{j}}\text{+}{{\text{c}}_{\text{3}}}\widehat{\text{k}}\] then $\overrightarrow{\text{a}} \times \overrightarrow{\text{b}} \times \overrightarrow{\text{c}}$ $= \left|\begin{array}{ccc} a_{1} & a_{2} & a \\ b_{1} & b_{2} & b \\ c_{1} & c_{2} & c \end{array}\right|$

• Scalar product of three vectors, two of which are equal or parallel is \[\text{0}\].

• Vectors \[\overrightarrow{\text{a}},\overrightarrow{\text{b}},\overrightarrow{\text{c}}\] are coplanar if \[\left[ \overrightarrow{\text{a}}\text{ }\overrightarrow{\text{b}}\text{ }\overrightarrow{\text{c}} \right]\text{=0}\].

Vector Algebra Class 12 Notes Maths - Basic Subjective Questions

Section–A (1 Mark Questions)

1. Find the values of x  and y so that the vectors $2 \hat{i}+3\hat{j}$ and $x \hat{i}+y\hat{j}$ are equal.

Ans. We know that

$$\begin{aligned}& a_1 \hat{i}+b_1 j=a_2 \hat{i}+b_2 j \\& \Leftrightarrow a_1=a_2 \text { and } b_1=b_2 \\& \therefore 2 \hat{i}+3\hat{j}=x \hat{i}+y\hat{j} \\& \Rightarrow x=2 \text { and } y=3 .\end{aligned}$$

2. Find a unit vector parallel to the vector $-3\hat{i}+4\hat{j}$. 

Ans. Let, $\vec{a}=-3 \hat{i}+4 j$.

Then,

$|\vec{a}|=\sqrt{(-3)^2+(4)^2}=5$

$\therefore$ Unit vector parallel to

$\vec{a}=a=\frac{\vec{a}}{|\vec{a}|}=\frac{1}{5}(-3 \hat{i}+4 j)=-\frac{3}{5}\hat{i}+\frac{4}{5} j .$

3. The magnitude of the vector $\bar{a}=3 \hat{i}-6 j+2 k$  is.

Ans. Let $\bar{a}=3 \hat{i}-6 j+2 k$. Then,

$|a|=\sqrt{3^2+(-6)^2+2^2}=7 \text {. }$

4. Find the projection of the vector $\bar{a}=2 \hat{i}+3\hat{j}+2\hat{k}$ on the vector $\bar{b}=\hat{i}+2\hat{j}+\hat{k}$

Ans. The projection of vector $\vec{a}$ on the vector $\vec{b}$ is given by -

$\frac{1}{\mid \vec{b}}(\vec{a} \cdot \vec{b})=\frac{(2 \times 1+3 \times 2+2 \times1)}{\sqrt{(1)^2+(2)^2+(1)^2}}=\frac{10}{\sqrt{6}}=\frac{5}{3} \sqrt{6}$

5.  If l,m  and n are direction cosines of a given vector, then l2+m2+n2= ________.

Ans. We know that,

If $l, m$ and $n$ represents direction cosines of a given vector.

Then,

$l^2+m^2+n^2=1 \text {. }$

Section–2 (2 Mark Questions)

6. If the position vector $\vec{a}$ of a point (12,n) is such that $\left | \vec{a} \right |=13$,  find the value of n. 

Ans. The position vector of the point $(12, n)$ is $12 \hat{i}+n j$.

$\begin{aligned}& \therefore \vec{a}=12 \hat{i}+n j \\& \Rightarrow|\vec{a}|=\sqrt{12^2+n^2}\end{aligned}$

$|\vec{a}|=13$

$\Rightarrow 13=\sqrt{12^2+n^2}$

$\Rightarrow 169=144+n^2$

$\Rightarrow n^2=25$

$\Rightarrow n= \pm 5$

7. Find the sum of vectors $\hat{a}=\hat{i}-2\hat{i}+\hat{k}, \hat{b}=-2\hat{i}+4\hat{j}+5\hat{k}, \hat{c}=\hat{i}-6\hat{j}-7\hat{k}$.

Ans. We have,

$\begin{aligned}& \vec{a}+\vec{b}+\vec{c}=(\vec{a}+\vec{b})+\vec{c} \\& \Rightarrow \vec{a}+\vec{b}+\vec{c}=\{(\hat{i}-2 j+k)+(-2 \hat{i}+4 j+5 k)\}+(\hat{i}-6 j-7 k) \\& \Rightarrow \vec{a}+\vec{b}+\vec{c}=\{(1-2) \vec{i}+(-2+4) j+(1+5) k\}+(\hat{i}-6 j-7 k) \\& \Rightarrow \vec{a}+\vec{b}+\vec{c}=(-\hat{i}+2 j+6 k)+(\hat{i}-6 j-7 k) \\& \Rightarrow \vec{a}+\vec{b}+\vec{c}=(-1+1) \hat{i}+(2-6) j+(6-7) k \\& \Rightarrow \vec{a}+\vec{b}+\vec{c}=0 \hat{i}-4 j-k .\end{aligned}$

8. Find a vector in the direction of vector \vec{a}=\hat{i}-2 \hat{j} that has magnitude 7 units.

Ans. Given: $\vec{a}=\hat{i}-2 \hat{j}$

$\therefore|\vec{a}|=\sqrt{1^2+(-2)^2}=\sqrt{5}$

The unit vector in the direction of the a given vector $\dot{a}$ is

$\hat{a}=\frac{1}{|\vec{a}|}=\frac{1}{\sqrt{5}}(\hat{i}-2\hat{j})=\frac{1}{\sqrt{5}}\hat{i}-\frac{2}{\sqrt{5}} \hat{j}$

Therefore, the vector having magnitude equal to 7 and in the direction of $\vec{a}$ is

$7 \hat{a}=7\left(\frac{1}{\sqrt{5}} \hat{i}-\frac{2}{\sqrt{5}}\hat{j}\right)=\frac{7}{\sqrt{5}} \hat{i}-\frac{14}{\sqrt{5}} \hat{j}$

9. If a vector makes angles $\alpha ,\beta ,\gamma$ with OX, OY, and OZ respectively, prove that $sin^{2}\alpha +sin^{2}\beta +sin^{2}\gamma =2$ . 

Ans. Let $l, m, n$ be the direction cosines of the given vector. Then,

$l=\cos \alpha, m=\cos \beta, n=\cos \gamma .$

Now, $l^2+m^2+n^2=1$

$\begin{aligned}& \Rightarrow \cos ^2 \alpha+\cos ^2 \beta+\cos ^2 \gamma=1 \\& \Rightarrow\left(1-\sin ^2 \alpha\right)+\left(1-\sin ^2 \beta\right)+\left(1-\sin ^2\gamma\right)=1 \\& \Rightarrow \sin ^2 \alpha+\sin ^2 \beta+\sin ^2 \gamma=2 .\end{aligned}$

10. Find $(\vec{a} + 3\vec{b}).(2\vec{a} - \vec{b})$ if $\vec{a}=\hat{i}+\hat{j}+2\hat{k}$ and $\vec{b}=3\hat{i}+2\hat{j}-\hat{k}$. 

Ans. Given:

$\vec{a}=\hat{i}+j+2 k$ and $\vec{b}=3 \hat{i}+2 j-k$.

$\Rightarrow \vec{a}+3 \vec{b}=(\hat{i}+j+2 k)+3(3 \hat{i}+2 j-k)=10 \hat{i}+7 j-k$

And,

$\therefore ( 2 \vec{a}-\vec{b}=2(\hat{i}+j+2 k)-(3 \hat{i}+2 j-k)=-\hat{i}+0 j+5 k )$

$\therefore ( 2 \vec{a}-\vec{b}=2(\hat{i}+j+2 k)-(3 \hat{i}+2 j-k)=-\hat{i}+0 j+5 k )$

=(10)(-1)+(7)(0)+(-1)(5)

=-10+0-5

=-15

11. For given vectors, $\vec{a}=2\hat{i}-\hat{}{j}+2\hat{k} a$ and $\vec{b}=-\hat{i}+\hat{j}-\hat{k}$, find the unit vector in the direction of the vector $\vec{a}+\vec{b}$ . 

Ans. The given vectors are

$\vec{a}=2 \hat{i}-j+2 k \text { and } \vec{b}=-\hat{i}+j-k$

$\therefore \vec{a}+\vec{b}=(2-1) \hat{i}+(-1+1) j+(2-1) k$

$=\hat{i}+k$

$|\vec{a}+\vec{b}|=\sqrt{1^2+1^2}-\sqrt{2}$

Hence, the unit vector in the direction of $\vec{a}+\vec{b}$ is

$\frac{\vec{a}+\vec{b}}{|\vec{a}+\vec{b}|}=\frac{\hat{i}+k}{\sqrt{2}}=\frac{1}{\sqrt{2}}\hat{i}+\frac{1}{\sqrt{2}} k \text {. }$

12. Find the magnitude of $\vec{a}$  given by $\vec{a}=(\hat{i}+3\hat{j}-2\hat{k})\times(-1\hat{i}+3\hat{k})$

Ans. We have,

$\begin{aligned}& \vec{a}=(\hat{i}+3 j-2 k) \times(-\hat{i}+0 j+3 k) \\& \Rightarrow \vec{a}=\left|\begin{array}{ccc}\hat{i} & j & k \\1 & 3 & -2 \\-1 & 0 & 3\end{array}\right|=(9-0) \hat{i}-(3-2) j+(0+3) k \\& =9 \hat{i}-j+3 k \\& \therefore|\vec{a}|=\sqrt{9^2+(-1)^2+3^2}=\sqrt{91} .\end{aligned}$

13. Find a unit vector perpendicular to both the vectors $\hat{i}-2\hat{j}+3\hat{k}$ and $\hat{i}+2\hat{j}-\hat{k}$. 

Ans. Let $\vec{a}=\hat{i}-2 \hat{j}+3 \hat{k}$ and $\vec{b}=\hat{i}+2 \hat{j}-\hat{k}$.

Then,

$\begin{aligned}& \vec{a} \times \vec{b}=\left|\begin{array}{ccc}\hat{i} & \hat{j} & \hat{k} \\1 & -2 & 3 \\1 & 2 & -1\end{array}\right|=(2-6) \hat{i}-(-1-3) \hat{j}+(2+2) \hat{k} \\& =-4 \hat{i}+4 \hat{j}+4 \hat{k} . \\& \Rightarrow|\vec{a} \times \vec{b}|=\sqrt{(-4)^2+4^2+4^2}=4 \sqrt{3} .\end{aligned}$

So, a unit vector perpendicular to both the vectors $\vec{a}$ and $\vec{b}$ is given by

$\hat{n}=\frac{\vec{a} \times \vec{b}}{|\vec{a} \times \vec{b}|}=\frac{(-4 \hat{i}+4\hat{j}+4 \hat{k})}{4 \sqrt{3}}=\frac{1}{\sqrt{3}}(-\hat{i}+\hat{j}+\hat{k})$

Importance of Chapter 10 Vector Algebra Class 12 Notes

Understanding Chapter 10: Vector Algebra is crucial for several reasons:

1. Foundation for Advanced Topics:

• Vector algebra forms the basis for more advanced topics in mathematics and science, including physics and engineering. Mastering this chapter is essential for tackling these higher-level subjects.

2. Real-World Applications:

• Vectors are used in various real-world applications, such as in physics to describe forces and motion and in computer graphics for modelling and animations. Knowing how to work with vectors is valuable in these fields.

3. Problem-Solving Skills:

• The concepts of vector addition, subtraction, and multiplication enhance problem-solving skills and mathematical reasoning, which are important for academic and practical scenarios.

4. Exam Preparation:

• Vector algebra is a key topic in Class 12 exams. Detailed notes help you understand core concepts, practice solving different types of problems, and prepare effectively for tests and exams.

5. Conceptual Clarity:

• Comprehensive notes provide clear explanations and practical examples, helping you build a solid understanding of vectors and their properties, which is crucial for academic success.

Important Formulas of Class 12 Maths Chapter 10 You Shouldn’t Miss!

Here are the important formulas for Class 12 Chapter 10: Vector Algebra that you shouldn’t miss:

1. Vector Addition:

If $\mathbf{a}$ and $\mathbf{b}$ are vectors, then their sum is:

\[\mathbf{a} + \mathbf{b}\]

2. Vector Subtraction:

For vectors $\mathbf{a}$ and $\mathbf{b}$, the difference is:

\[\mathbf{a} - \mathbf{b}\]

3. Scalar Multiplication:

If $\mathbf{a}$ is a vector and $k$ is a scalar, then:

\[k\mathbf{a}\]

4. Dot Product (Scalar Product):

For vectors $\mathbf{a} = a_1\mathbf{i} + a_2\mathbf{j} + a_3\mathbf{k}$ and $\mathbf{b} = b_1\mathbf{i} + b_2\mathbf{j} + b_3\mathbf{k}$:

\[\mathbf{a} \cdot \mathbf{b} = a_1b_1 + a_2b_2 + a_3b_3\]

5. Cross Product (Vector Product):

For vectors $\mathbf{a}$ and $\mathbf{b}$:

\[\mathbf{a} \times \mathbf{b} = \begin{vmatrix}\mathbf{i} & \mathbf{j} & \mathbf{k} \\a_1 & a_2 & a_3 \\b_1 & b_2 & b_3 \end{vmatrix}\]

This results in a vector perpendicular to both $\mathbf{a}$ and $\mathbf{b}$.

6. Magnitude of a Vector:

For vector $\mathbf{a} = a_1\mathbf{i} + a_2\mathbf{j} + a_3\mathbf{k}$:

\[|\mathbf{a}| = \sqrt{a_1^2 + a_2^2 + a_3^2}\]

7. Unit Vector:

A unit vector in the direction of vector $\mathbf{a}$:

\[\hat{\mathbf{a}} = \frac{\mathbf{a}}{|\mathbf{a}|}\]

8. Angle Between Two Vectors:

For vectors $\mathbf{a}$ and $\mathbf{b}$:

\[\cos \theta = \frac{\mathbf{a} \cdot \mathbf{b}}{|\mathbf{a}| |\mathbf{b}|}\]

Here, $\theta$ is the angle between $\mathbf{a}$ and $\mathbf{b}$.

9. Projection of $\mathbf{a}$ on $\mathbf{b}$:

The projection of $\mathbf{a}$ on $\mathbf{b}$ is:

\[\text{Proj}_{\mathbf{b}} \mathbf{a} = \frac{\mathbf{a} \cdot \mathbf{b}}{|\mathbf{b}|^2} \mathbf{b}\]

10. Vector Triple Product:

For vectors $\mathbf{a}$, $\mathbf{b}$, and $\mathbf{c}$:

\[\mathbf{a} \times (\mathbf{b} \times \mathbf{c}) = (\mathbf{a} \cdot \mathbf{c}) \mathbf{b} - (\mathbf{a} \cdot \mathbf{b}) \mathbf{c}\]

Tips for Learning the Class 12 Maths Chapter 10 Vector Algebra

Here are some effective tips for learning Class 12 Maths Chapter 10: Vector Algebra:

1. Understand Basic Concepts:

• Begin by understanding the fundamental concepts of vectors, including their definition, representation, and basic operations. Grasping these basics is crucial for solving more complex problems.

2. Familiarise with Vector Operations:

• Learn how to perform vector addition, subtraction, and scalar multiplication. Practice these operations with different examples to build a solid foundation.

3. Master Dot and Cross Products:

• Study the formulas and methods for calculating dot products and cross products. These are essential for solving many problems in vector algebra.

4. Practice Vector Magnitudes and Directions:

• Understand how to find the magnitude and direction of a vector. Practice problems that involve calculating the length of vectors and using unit vectors.

5. Use Geometric Interpretations:

• Visualise vectors geometrically. Understanding how vectors interact in space can help you better grasp their properties and applications.

Conclusion

Mastering Vector Algebra is crucial for solving complex problems in mathematics and its applications. By utilising the provided notes and PDFs, you gain access to clear explanations, essential formulas, and practical examples that will enhance your understanding and exam preparation. Consistent study and practice using these resources will help you excel in your Class 12 mathematics course and build a strong foundation for future studies. 

Related Study Materials for Class 12 Maths Chapter 10 Vector Algebra

Students can also download additional study materials provided by Vedantu for Class 12 Maths Chapter 10 Vector Algebra.

Chapter-wise Revision Notes Links for Class 12 Maths

Important Study Materials for Class 12 Maths