Important Questions for CBSE Class 12 Maths Chapter 10 - Vector Algebra 2024-25

Very Short Answer Questions (1 Mark)

1. What are the horizontal and vertical components of a vector \[\overrightarrow a \] of magnitude \[5\] making an angle of \[{150^ \circ }\] with the direction of x-axis?

Ans: The vector \[\overrightarrow a \] has a magnitude \[|\overrightarrow a | = 5\] units and makes an angle \[\theta  = {150^ \circ }\] in the direction of the x-axis. Its horizontal and vertical components can be calculated as follows:

Horizontal component \[x = |\overrightarrow a | \cdot \cos \theta \]

\[ \Rightarrow x = 5 \cdot (\cos {150^ \circ })\]

\[ \Rightarrow x = 5 \cdot ( - \cos {30^ \circ })\]

\[ \Rightarrow x = 5 \cdot ( - \frac{{\sqrt 3 }}{2})\]

\[ \Rightarrow x =  - \frac{{5\sqrt 3 }}{2}\]

Vertical component \[y = |\overrightarrow a | \cdot \sin \theta \]

\[ \Rightarrow y = 5 \cdot (\sin {150^ \circ })\]

\[ \Rightarrow y = 5 \cdot (\sin {30^ \circ })\]

\[ \Rightarrow y = 5 \cdot (\frac{1}{2})\]

\[ \Rightarrow y = \frac{5}{2}\]

2. What is \[a \in R\] such that \[|a\overrightarrow x | = 1\] , where \[\overrightarrow x  = \hat i - 2\hat j + 2\hat k\] ?

Ans: We know that \[\overrightarrow x  = \hat i - 2\hat j + 2\hat k\] , so we can calculate \[|\overrightarrow x |\] as:

\[|\overrightarrow x | = \sqrt {{1^2} + {{( - 2)}^2} + {2^2}} \]

\[|\overrightarrow x | = \sqrt {1 + 4 + 4} \]

\[|\overrightarrow x | = \sqrt 9 \]

\[|\overrightarrow x | = 3\] units

Now we have \[|a\overrightarrow x | = 1\] and \[|\overrightarrow x | = 3\].

\[ \Rightarrow |a(3)| = 1\]

\[ \Rightarrow |a| = \frac{1}{3}\]

\[ \Rightarrow a =  \pm \frac{1}{3}\]

3. When is \[\mathbf{|\overrightarrow x  + \overrightarrow y | = |\overrightarrow x | + |\overrightarrow y |}\] ?

Ans: The magnitude of sum of two vectors can be equal to sum of their individual magnitude if and only if the two vectors are parallel.

4. What is the area of a parallelogram whose sides are given by \[\mathbf{2\hat i - \hat j}\] and \[\mathbf{\hat i + 5\hat k}\] ?

Ans: Let a parallelogram with adjacent sides \[\overrightarrow a  = 2\hat i - \hat j\] and \[\overrightarrow b  = \hat i + 5\hat k\] have an area of \[\overrightarrow a  \times \overrightarrow b \] . We calculate the value of \[\overrightarrow a  \times \overrightarrow b \] as follows:

\[\overrightarrow a  \times \overrightarrow b  = \left( {\begin{array}{*{20}{c}} {\hat i}&{\hat j}&{\hat k}\\ 2&{ - 1}&0\\ 1&0&5 \end{array}} \right)\]

\[ \Rightarrow \overrightarrow a  \times \overrightarrow b  = \hat i( - 5) - \hat j(10) + \hat k(1)\]

\[ \Rightarrow \overrightarrow a  \times \overrightarrow b  =  - 5\hat i - 10\hat j + \hat k\]

\[ \Rightarrow |\overrightarrow a  \times \overrightarrow b | = \sqrt {{{( - 5)}^2} + {{( - 10)}^2} + {1^2}} \]

\[ \Rightarrow |\overrightarrow a  \times \overrightarrow b | = \sqrt {25 + 100 + 1} \]

\[ \Rightarrow |\overrightarrow a  \times \overrightarrow b | = \sqrt {126} \] units

5. What is the angle between \[\mathbf{\overrightarrow a} \] and \[\mathbf{\overrightarrow b} \] if \[\mathbf{\overrightarrow a  \cdot \overrightarrow b  = 3}\] and \[\mathbf{|\overrightarrow a  \times \overrightarrow b | = 3\sqrt 3} \] ?

Ans: We know that \[\overrightarrow a  \cdot \overrightarrow b  = |\overrightarrow a ||\overrightarrow b |\cos \theta \] and \[\overrightarrow a  \cdot \overrightarrow b  = 3\] is given.

So, \[|\overrightarrow a ||\overrightarrow b |\cos \theta  = 3\] .

\[ \Rightarrow \cos \theta  = \frac{3}{{|\overrightarrow a ||\overrightarrow b |}}\] ……(1)

Further, \[\overrightarrow a  \times \overrightarrow b  = |\overrightarrow a ||\overrightarrow b |\sin \theta \] and \[\overrightarrow a  \times \overrightarrow b  = 3\sqrt 3 \] . 

So, \[|\overrightarrow a ||\overrightarrow b |\sin \theta  = 3\sqrt 3 \]

\[ \Rightarrow \frac{{\sin \theta }}{{\sqrt 3 }} = \frac{3}{{|\overrightarrow a ||\overrightarrow b |}}\] ……(2)

From (1) and (2) we get:

\[\frac{{\sin \theta }}{{\sqrt 3 }} = \cos \theta \]

\[ \Rightarrow \frac{{\sin \theta }}{{\cos \theta }} = \sqrt 3 \]

\[ \Rightarrow \tan \theta  = \sqrt 3 \]

\[ \Rightarrow \theta  = \frac{\pi }{3}\]

6. Write a unit vector which makes an angle of \[\frac{\pi }{4}\] with x-axis and \[\frac{\pi }{3}\] with z-axis and an acute angle with y-axis.

Ans: It is given that \[\alpha  = \frac{\pi }{4}\] is the angle that the vector makes with x-axis, \[\gamma  = \frac{\pi }{3}\] with z-axis and an acute angle \[\beta \] with y-axis.

We know that \[{\cos ^2}\alpha  + {\cos ^2}\beta  + {\cos ^2}\gamma  = 1\]

So, \[{\cos ^2}\frac{\pi }{4} + {\cos ^2}\beta  + {\cos ^2}\frac{\pi }{3} = 1\]

\[ \Rightarrow {\left( {\frac{1}{{\sqrt 2 }}} \right)^2} + {\cos ^2}\beta  + {(\frac{1}{2})^2} = 1\]

\[ \Rightarrow \frac{1}{2} + {\cos ^2}\beta  + \frac{1}{4} = 1\]

\[ \Rightarrow {\cos ^2}\beta  = \frac{1}{4}\]

\[ \Rightarrow \cos \beta  =  \pm \frac{1}{2}\]

\[ \Rightarrow \beta  = \frac{\pi }{3} since \beta is acute angle \] 

We can find the unit vector making the above angles with the axes as follows:

\[\hat a = \cos \alpha  \cdot \hat i + \cos \beta  \cdot \hat j + \cos \gamma  \cdot \hat k\]

\[ \Rightarrow \hat a = \frac{1}{2}\hat i + \frac{1}{2}\hat j + \frac{1}{2}\hat k\]

7. If A is the point (4,5) and vector \[\mathbf{\overrightarrow {AB} }\] has components \[2\] and \[6\] along x-axis and y-axis respectively then write point B.

Ans: Since point A is \[(4,5)\] , we can write \[\overrightarrow {OA}  = 4\hat i + 5\hat j\] . Further, it is given that \[\overrightarrow {AB}  = 2\hat i + 6\hat j\] .

Let \[\overrightarrow {OB}  = x\hat i + y\hat j\] .

Now, \[\overrightarrow {AB}  = \overrightarrow {OB}  - \overrightarrow {OA} \] .

\[ \Rightarrow (2\hat i + 6\hat j) = (x\hat i + y\hat j) - (4\hat i + 5\hat j)\]

\[ \Rightarrow (x\hat i + y\hat j) = (2\hat i + 6\hat j) + (4\hat i + 5\hat j)\]

\[ \Rightarrow x\hat i + y\hat j = 6\hat i + 11\hat j\]

Hence, point B is \[(6,11)\] .

8. What is the point of trisection of PQ nearer to P if positions of P and Q are \[ \mathbf{3\hat i + 3\hat j - 4\hat k}\] and \[\mathbf{9\hat i + 8\hat j - 10\hat k}\] respectively?

Ans:  It is given that \[\overrightarrow {OP}  = 3\hat i + 3\hat j - 4\hat k\] and \[\overrightarrow {OQ}  = 9\hat i + 8\hat j - 10\hat k\] .

Now, \[\overrightarrow {PQ}  = \overrightarrow {OQ}  - \overrightarrow {OP} \] .

\[ \Rightarrow \overrightarrow {PQ}  = (9\hat i + 8\hat j - 10\hat k) - (3\hat i + 3\hat j - 4\hat k)\]

\[ \Rightarrow \overrightarrow {PQ}  = 6\hat i + 5\hat j - 6\hat k\]

Let the point of trisection nearer to P be A. 

So, \[3\overrightarrow {PA}  = \overrightarrow {PQ} \]

\[ \Rightarrow \overrightarrow {PA}  = \frac{{\overrightarrow {PQ} }}{3}\]

\[ \Rightarrow \overrightarrow {PA}  = \frac{{6\hat i + 5\hat j - 6\hat k}}{3}\]

\[ \Rightarrow \overrightarrow {PA}  = 2\hat i + \frac{5}{2}\hat j - 2\hat k\]

Hence, the point of trisection of \[\overrightarrow {PQ} \] nearer to P is \[(2,\frac{5}{2}, - 2)\] .

9. Write the vector in the direction of \[\mathbf{2\hat i + 3\hat j + 2\sqrt 3 \hat k}\] , whose magnitude is \[\mathbf{10}\] units.

Ans: Let the vector \[\overrightarrow a \] be \[2\hat i + 3\hat j + 2\sqrt 3 \hat k\] .

The unit vector in its direction will hence be-

\[\hat a = \frac{{2\hat i + 3\hat j + 2\sqrt 3 \hat k}}{{\sqrt {{2^2} + {3^2} + {{(2\sqrt 3 )}^2}} }}\]

\[ \Rightarrow \hat a = \frac{{2\hat i + 3\hat j + 2\sqrt 3 \hat k}}{{\sqrt {4 + 9 + 12} }}\]

\[\hat a = \frac{{2\hat i + 3\hat j + 2\sqrt 3 \hat k}}{{\sqrt {25} }}\]

\[\hat a = \frac{{2\hat i + 3\hat j + 2\sqrt 3 \hat k}}{5}\]

A vector \[\overrightarrow x \] in the direction of \[\overrightarrow a \] and with a magnitude \[10\] units will be-

\[\overrightarrow x  = \frac{{2\hat i + 3\hat j + 2\sqrt 3 \hat k}}{5} \times 10\]

\[ \Rightarrow \overrightarrow x  = 2(2\hat i + 3\hat j + 2\sqrt 3 \hat k)\]

\[ \Rightarrow \overrightarrow x  = 4\hat i + 6\hat j + 4\sqrt 3 \hat k\]

10. What are the direction cosines of a vector equiangular with coordinate

axes?

Ans: Let all the direction cosines of the vector be equal to \[\alpha \] .

Therefore, \[l = m = n = \cos \alpha \] .

We know that \[{l^2} + {m^2} + {n^2} = 1\] .

\[ \Rightarrow {\cos ^2}\alpha  + {\cos ^2}\alpha  + {\cos ^2}\alpha  = 1\]

\[ \Rightarrow 3{\cos ^2}\alpha  = 1\]

\[ \Rightarrow {\cos ^2}\alpha  = \frac{1}{3}\]

\[ \Rightarrow \cos \alpha  =  \pm \frac{1}{{\sqrt 3 }}\]

Thus, direction cosines of the vector which is equiangular to all three coordinate axes are \[ \pm \frac{1}{{\sqrt 3 }}\] , \[ \pm \frac{1}{{\sqrt 3 }}\] and \[ \pm \frac{1}{{\sqrt 3 }}\] .

11. What is the angle which the vector \[\mathbf{3\hat i - 6\hat j + 2\hat k}\] makes with the x-axis?

Ans: We have the vector \[\overrightarrow v  = 3\hat i - 6\hat j + 2\hat k\] .

To determine the angle it makes with the x-axis, we calculate the direction cosine with the required axis. So, we need to find \[l = \frac{a}{{|\overrightarrow v |}}\] , where \[l\] is the direction cosine with x-axis and \[a\] is the component corresponding to it.

Now, \[l = \frac{a}{{|\overrightarrow v |}}\]

\[ \Rightarrow l = \frac{3}{{\sqrt {{3^2} + {{( - 6)}^2} + {2^2}} }}\]

\[ \Rightarrow l = \frac{3}{{\sqrt {9 + 36 + 4} }}\]

\[ \Rightarrow l = \frac{3}{{\sqrt {49} }}\]

\[ \Rightarrow l = \frac{3}{7}\]

Further, \[l = \cos \alpha \] , where \[\alpha \] is the angle the vector makes with the x-axis.

Thus, \[\cos \alpha  = \frac{3}{7}\]

\[ \Rightarrow \alpha  = {\cos ^{ - 1}}(\frac{3}{7})\]

The vector \[\overrightarrow v  = 3\hat i - 6\hat j + 2\hat k\] makes an angle of \[{\cos ^{ - 1}}(\frac{3}{7})\] with the x-axis.

12. Write a unit vector perpendicular to both the vectors \[\mathbf{3\hat i - 2\hat j + \hat k}\] and \[ \mathbf{- 2\hat i + \hat j - 2\hat k}\] .

Ans: Given vectors \[\overrightarrow a  = 3\hat i - 2\hat j + \hat k\] and \[\overrightarrow b  =  - 2\hat i + \hat j - 2\hat k\] .

Firstly, we find the cross product of the two vectors:

\[\overrightarrow a  \times \overrightarrow b  = \left( {\begin{array}{*{20}{c}} {\hat i}&{\hat j}&{\hat k}\\ 3&{ - 2}&1\\ { - 2}&1&{ - 2} \end{array}} \right)\]

\[ \Rightarrow \overrightarrow a  \times \overrightarrow b  = \hat i(3) - \hat j( - 4) + \hat k( - 1)\]

\[ \Rightarrow \overrightarrow a  \times \overrightarrow b  = 3\hat i + 4\hat j - \hat k\]

Now, the required unit vector which is perpendicular to both the given vectors can be calculated as \[\frac{{\overrightarrow a  \times \overrightarrow b }}{{|\overrightarrow a  \times \overrightarrow b |}}\] 

\[ \Rightarrow \frac{{\overrightarrow a  \times \overrightarrow b }}{{|\overrightarrow a  \times \overrightarrow b |}} = \frac{{3\hat i + 4\hat j - \hat k}}{{\sqrt {{3^2} + {4^2} + {{( - 1)}^2}} }}\]

\[ \Rightarrow \frac{{\overrightarrow a  \times \overrightarrow b }}{{|\overrightarrow a  \times \overrightarrow b |}} = \frac{{3\hat i + 4\hat j - \hat k}}{{\sqrt {9 + 16 + 1} }}\]

\[ \Rightarrow \frac{{\overrightarrow a  \times \overrightarrow b }}{{|\overrightarrow a  \times \overrightarrow b |}} = \frac{{3\hat i + 4\hat j - \hat k}}{{\sqrt {26} }}\]

\[ \Rightarrow \frac{{\overrightarrow a  \times \overrightarrow b }}{{|\overrightarrow a  \times \overrightarrow b |}} = \frac{{3\hat i + 4\hat j - \hat k}}{{\sqrt {26} }}\]

Hence, the required vector is \[\frac{{3\hat i + 4\hat j - \hat k}}{{\sqrt {26} }}\] .

13. What is the projection of the vector \[\mathbf{\hat i - \hat j}\] on the vector \[\mathbf{\hat i + \hat j}\] ?

Ans: Let \[\overrightarrow a  = \hat i - \hat j\] and \[\overrightarrow b  = \hat i + \hat j\] .

Projection of vector \[\overrightarrow a \] on \[\overrightarrow b \] \[ = \frac{{\overrightarrow a  \cdot \overrightarrow b }}{{|\overrightarrow b |}}\]

\[ \Rightarrow \frac{{\overrightarrow a  \cdot \overrightarrow b }}{{|\overrightarrow b |}} = \frac{{(1)(1) + ( - 1)(1) + (0)(0)}}{{\sqrt {{1^2} + {1^2}} }}\]

\[ \Rightarrow \frac{{\overrightarrow a  \cdot \overrightarrow b }}{{|\overrightarrow b |}} = \frac{{1 - 1}}{{\sqrt 2 }}\]

\[ \Rightarrow \frac{{\overrightarrow a  \cdot \overrightarrow b }}{{|\overrightarrow b |}} = 0\]

The projection of vector \[\overrightarrow a \] on \[\overrightarrow b \] is \[0\] .

14. If \[\mathbf{|\overrightarrow a | = 2}\] , \[\mathbf{|\overrightarrow b | = 2\sqrt 3} \] and \[\mathbf{\overrightarrow a  \bot \overrightarrow b }\] , what is the value of \[\mathbf{|\overrightarrow a  + \overrightarrow b |}\] ?

Ans: Taking the square of \[|\overrightarrow a  + \overrightarrow b |\] :

\[|\overrightarrow a  + \overrightarrow b {|^2} = |\overrightarrow a  + \overrightarrow b | \cdot |\overrightarrow a  + \overrightarrow b |\]

\[ \Rightarrow |\overrightarrow a  + \overrightarrow b {|^2} = \overrightarrow a  \cdot \overrightarrow a  + \overrightarrow a  \cdot \overrightarrow b  + \overrightarrow b  \cdot \overrightarrow a  + \overrightarrow b  \cdot \overrightarrow b \]

Since \[\overrightarrow a \] and \[\overrightarrow b \] are perpendicular, their dot product is equal to zero.

Further, we know that the dot product of a vector with itself is equal to the square of its magnitude.

\[ \Rightarrow |\overrightarrow a  + \overrightarrow b {|^2} = |\overrightarrow a {|^2} + |\overrightarrow b {|^2}\]

\[ \Rightarrow |\overrightarrow a  + \overrightarrow b {|^2} = {2^2} + {(2\sqrt 3 )^2}\]

\[ \Rightarrow |\overrightarrow a  + \overrightarrow b {|^2} = 4 + 12\]

\[ \Rightarrow |\overrightarrow a  + \overrightarrow b {|^2} = 16\]

Hence, \[|\overrightarrow a  + \overrightarrow b | = 4\] .

15. For what value of \[\mathbf{\lambda }\] is \[\mathbf{\overrightarrow a  = \lambda \hat i + \hat j + 4\hat k}\] perpendicular to \[\mathbf{\overrightarrow b  = 2\hat i + 6\hat j + 3\hat k}\] ?

Ans: For \[\overrightarrow a \] to be perpendicular to \[\overrightarrow b \] , their dot product should be zero.

So, \[\overrightarrow a  \cdot \overrightarrow b  = {a_1}{a_2} + {b_1}{b_2} + {c_1}{c_2}\]

\[ \Rightarrow \overrightarrow a  \cdot \overrightarrow b  = \lambda (2) + (1)(6) + (4)(3)\] 

\[ \Rightarrow \overrightarrow a  \cdot \overrightarrow b  = 2\lambda  + 6 + 12\]

\[ \Rightarrow \overrightarrow a  \cdot \overrightarrow b  = 2\lambda  + 18\]

Now, \[\overrightarrow a  \cdot \overrightarrow b  = 0\]

Hence, \[2\lambda  + 18 = 0\]

\[ \Rightarrow \lambda  =  - \frac{{18}}{2}\]

\[ \Rightarrow \lambda  =  - 9\]

16. What is \[\mathbf{|\overrightarrow a |}\] , if \[\mathbf{(\overrightarrow a  + \overrightarrow b ) \cdot (\overrightarrow a  - \overrightarrow b ) = 3}\] and \[\mathbf{2|\overrightarrow b | = |\overrightarrow a |}\] ?

Ans: It is given that \[(\overrightarrow a  + \overrightarrow b ) \cdot (\overrightarrow a  - \overrightarrow b ) = 3\]

\[ \Rightarrow \overrightarrow a  \cdot \overrightarrow a  - \overrightarrow a  \cdot \overrightarrow b  + \overrightarrow b  \cdot \overrightarrow a  + \overrightarrow b  \cdot \overrightarrow b  = 3\]

We know that the dot product of a vector with itself is equal to the square of its magnitude.

\[ \Rightarrow |\overrightarrow a {|^2} + |\overrightarrow b {|^2} = 3\]

\[ \Rightarrow |\overrightarrow a {|^2} + {\left( {\frac{{|\overrightarrow a |}}{2}} \right)^2} = 3\]  (Since \[2|\overrightarrow b | = |\overrightarrow a |\] )

\[ \Rightarrow |\overrightarrow a {|^2} + \frac{{|\overrightarrow a {|^2}}}{4} = 3\]

\[ \Rightarrow \frac{{5|\overrightarrow a {|^2}}}{4} = 3\]

\[ \Rightarrow |\overrightarrow a {|^2} = \frac{{12}}{5}\]

\[ \Rightarrow |\overrightarrow a | =  \pm \sqrt {\frac{{12}}{5}} \]

17. What is the angle between \[\mathbf{\overrightarrow a }\] and \[\mathbf{\overrightarrow b }\] , if \[\mathbf{|\overrightarrow a  - \overrightarrow b | = |\overrightarrow a  + \overrightarrow b |}\] ?

Ans: We have \[|\overrightarrow a  - \overrightarrow b | = |\overrightarrow a  + \overrightarrow b |\]

Squaring both sides,

\[ \Rightarrow |\overrightarrow a  - \overrightarrow b {|^2} = |\overrightarrow a  + \overrightarrow b {|^2}\]

\[ \Rightarrow |\overrightarrow a {|^2} + |\overrightarrow b {|^2} - 2\overrightarrow a  \cdot \overrightarrow b  = |\overrightarrow a {|^2} + |\overrightarrow b {|^2} + 2\overrightarrow a  \cdot \overrightarrow b \]

\[ \Rightarrow  - 2\overrightarrow a  \cdot \overrightarrow b  = 2\overrightarrow a  \cdot \overrightarrow b \]

\[ \Rightarrow 4\overrightarrow a  \cdot \overrightarrow b  = 0\]

\[ \Rightarrow \overrightarrow a  \cdot \overrightarrow b  = 0\]

Since the dot product of the two vectors is equal to zero, the given vectors are perpendicular. Hence, the angle between them is \[{90^ \circ }\] .

18. In a parallelogram ABCD, \[\mathbf{\overrightarrow {AB}  = 2\hat i - \hat j + 4\hat k}\] and \[\mathbf{\overrightarrow {AC}  = \hat i + \hat j + 4\hat k}\] . What is the length of the side BC?

Ans: We have \[\overrightarrow {AB}  = 2\hat i - \hat j + 4\hat k\] and \[\overrightarrow {AC}  = \hat i + \hat j + 4\hat k\] .

We calculate \[|\overrightarrow {AB} | = \sqrt {{2^2} + {{( - 1)}^2} + {4^2}} \]

\[ \Rightarrow |\overrightarrow {AB} | = \sqrt {21} \]

Similarly, \[|\overrightarrow {AC} | = \sqrt {{1^2} + {1^2} + {4^2}} \]

\[ \Rightarrow |\overrightarrow {AC} | = \sqrt {18} \]

In a parallelogram, AC would represent a diagonal and AB and BC would be adjacent sides.

So, \[|\overrightarrow {BC} | = |\overrightarrow {AC}  - \overrightarrow {AB} |\]

Squaring both sides:

\[ \Rightarrow |\overrightarrow {BC} {|^2} = |\overrightarrow {AC}  - \overrightarrow {AB} {|^2}\]

\[ \Rightarrow |\overrightarrow {BC} {|^2} = |\overrightarrow {AC} {|^2} + |\overrightarrow {AB} {|^2} - 2\overrightarrow {AC}  \cdot \overrightarrow {AB} \]

\[ \Rightarrow |\overrightarrow {BC} {|^2} = 18 + 21 - 2[(2)(1) + ( - 1)(1) + (4)(4)]\]

\[ \Rightarrow |\overrightarrow {BC} {|^2} = 39 - 2(17)\]

\[ \Rightarrow |\overrightarrow {BC} {|^2} = 39 - 34\]

\[ \Rightarrow |\overrightarrow {BC} {|^2} = 5\]

\[ \Rightarrow |\overrightarrow {BC} | = \sqrt 5 \]

19. What is the area of a parallelogram whose diagonals are given by vectors \[\mathbf{2\hat i + \hat j - 2\hat k}\] and \[ \mathbf{- \hat i + 2\hat k}\] ?

Ans: The two diagonals of a parallelogram are given by \[\overrightarrow a  = 2\hat i + \hat j - 2\hat k\] and \[\overrightarrow b  =  - \hat i + 2\hat k\] .

We find their cross product as follows:

\[\overrightarrow a  \times \overrightarrow b  = \left( {\begin{array}{*{20}{c}} {\hat i}&{\hat j}&{\hat k}\\ 2&1&{ - 2}\\ { - 1}&0&2 \end{array}} \right)\]

\[ \Rightarrow \overrightarrow a  \times \overrightarrow b  = \hat i(2) - \hat j(2) + \hat k(1)\]

\[ \Rightarrow \overrightarrow a  \times \overrightarrow b  = 2\hat i - 2\hat j + \hat k\]

Next, we find its magnitude:

\[ \Rightarrow |\overrightarrow a  \times \overrightarrow b | = \sqrt {{2^2} + {{( - 2)}^2} + {1^2}} \]

\[ \Rightarrow |\overrightarrow a  \times \overrightarrow b | = \sqrt {4 + 4 + 1} \]

\[ \Rightarrow |\overrightarrow a  \times \overrightarrow b | = \sqrt 9 \]

\[ \Rightarrow |\overrightarrow a  \times \overrightarrow b | = 3\]

The area of the parallelogram A can be calculated as:

\[A = \frac{1}{2} \cdot |\overrightarrow a  \times \overrightarrow b |\]

\[ \Rightarrow A = \frac{3}{2}\] square units

The area of the parallelogram with diagonals \[\overrightarrow a  = 2\hat i + \hat j - 2\hat k\] and \[\overrightarrow b  =  - \hat i + 2\hat k\] is \[\frac{3}{2}\] square units.

20. Find \[\mathbf{|\overrightarrow x |}\] if for a unit vector \[\mathbf{\hat a}\] , \[\mathbf{(\overrightarrow x  - \hat a) \cdot (\overrightarrow x  + \hat a) = 12}\] .

Ans: It is given that \[(\overrightarrow x  - \hat a) \cdot (\overrightarrow x  + \hat a) = 12\]

\[ \Rightarrow \overrightarrow x  \cdot \overrightarrow x  - \overrightarrow x  \cdot \hat a + \hat a \cdot \overrightarrow x  - \hat a \cdot \hat a = 12\]

We know that the dot product of a vector with itself is equal to the square of its magnitude.

\[ \Rightarrow |\overrightarrow x {|^2} - |\hat a{|^2} = 12\]

\[ \Rightarrow |\overrightarrow x {|^2} - {1^2} = 12\] (Since, magnitude of a unit vector is equal to one unit)

\[ \Rightarrow |\overrightarrow x {|^2} = 13\]

\[ \Rightarrow |\overrightarrow x | = \sqrt {13} \] units

21. If \[\overrightarrow a \] and \[\overrightarrow b \] are two unit vectors and \[\overrightarrow a  + \overrightarrow b \] is also a unit vector, then what is the angle between \[\overrightarrow a \] and \[\overrightarrow b \] ?

Ans: We know that \[\overrightarrow a  + \overrightarrow b \] , \[\overrightarrow a \] and \[\overrightarrow b \] are unit vectors.

Taking the square of \[\overrightarrow a  + \overrightarrow b \] :

\[|\overrightarrow a  + \overrightarrow b {|^2} = \overrightarrow a  \cdot \overrightarrow a  + 2\overrightarrow a  \cdot \overrightarrow b  + \overrightarrow b  \cdot \overrightarrow b \]

\[ \Rightarrow |\overrightarrow a  + \overrightarrow b {|^2} = |\overrightarrow a {|^2} + 2\overrightarrow a  \cdot \overrightarrow b  + |\overrightarrow b {|^2}\]

\[ \Rightarrow {1^2} = {1^2} + 2\overrightarrow a  \cdot \overrightarrow b  + {1^2}\] (Since magnitude of unit vectors is equal to one unit)

\[ \Rightarrow 2\overrightarrow a  \cdot \overrightarrow b  =  - 1\]

\[ \Rightarrow \overrightarrow a  \cdot \overrightarrow b  =  - \frac{1}{2}\]

Further, \[\overrightarrow a  \cdot \overrightarrow b  = |\overrightarrow a ||\overrightarrow b |\cos \theta \]

\[ \Rightarrow |\overrightarrow a ||\overrightarrow b |\cos \theta  =  - \frac{1}{2}\]

\[ \Rightarrow (1)(1)\cos \theta  =  - \frac{1}{2}\]

\[ \Rightarrow \cos \theta  =  - \frac{1}{2}\]

\[ \Rightarrow \theta  = \frac{{2\pi }}{3}\]

22. If \[\mathbf{\hat i,\hat j,\hat k}\] are the usual three mutually perpendicular unit vectors then what is the value of \[\mathbf{\hat i \cdot (\hat j \times \hat k) + \hat j \cdot (\hat i \times \hat k) + \hat k \cdot (\hat j \times \hat i)}\] ? 

Ans: We have \[\hat i \cdot (\hat j \times \hat k) + \hat j \cdot (\hat i \times \hat k) + \hat k \cdot (\hat j \times \hat i)\] .

It is known that \[\hat j \times \hat k = \hat i\] , \[\hat k \times \hat i = \hat j\] and \[\hat i \times \hat j = \hat k\] .

Therefore, \[\hat i \cdot (\hat j \times \hat k) + \hat j \cdot (\hat i \times \hat k) + \hat k \cdot (\hat j \times \hat i)\] can be rewritten as:

\[ = \hat i \cdot \hat i + \hat j \cdot ( - \hat j) + \hat k \cdot ( - \hat k)\]

\[= \hat i \cdot \hat i - \hat j \cdot \hat j - \hat k \cdot \hat k\]

\[ = 1 - 1 - 1\] (Since \[\hat i \cdot \hat i = \hat j \cdot \hat j = \hat k \cdot \hat k = 1\] )

\[ =  - 1\]

23. What is the angle between \[\mathbf{\overrightarrow x} \] and \[\mathbf{\overrightarrow y }\] if \[\mathbf{\overrightarrow x  \cdot \overrightarrow y  = |\overrightarrow x  \times \overrightarrow y |}\] ?

Ans: The dot product and cross product of the given vectors \[\overrightarrow x \] and \[\overrightarrow y \] are equal. This implies:

\[\overrightarrow x  \cdot \overrightarrow y  = |\overrightarrow x  \times \overrightarrow y |\]

\[ \Rightarrow |\overrightarrow x ||\overrightarrow y |\cos \theta  = |\overrightarrow x ||\overrightarrow y |\sin \theta \]

\[ \Rightarrow \cos \theta  = \sin \theta \]

This is only possible if \[\theta  = \frac{\pi }{4}\] .

Hence, the angle between vectors \[\overrightarrow x \] and \[\overrightarrow y \] is \[\frac{\pi }{4}\] .

24. Write a unit vector in XY-plane, making an angle of \[{30^ \circ }\] with the positive direction of x–axis.

Ans: Let \[\overrightarrow r \] be a unit vector in the XY-plane, making an angle of \[{30^ \circ }\] with the positive direction of the x-axis. It will be represented as:

\[\overrightarrow r  = \cos \theta \hat i + \sin \theta \hat j\]

Substituting \[\theta  = {30^ \circ }\] :

\[ \Rightarrow \overrightarrow r  = \cos ({30^ \circ })\hat i + \sin ({30^ \circ })\hat j\]

\[ \Rightarrow \overrightarrow r  = \frac{{\sqrt 3 }}{2}\hat i + \frac{1}{2}\hat j\]

The required vector is \[\frac{{\sqrt 3 }}{2}\hat i + \frac{1}{2}\hat j\] .

25. If \[\mathbf{\overrightarrow a }\] , \[\mathbf{\overrightarrow b }\] and \[\mathbf{\overrightarrow c }\] are unit vectors with \[\mathbf{\overrightarrow a  + \overrightarrow b  + \overrightarrow c  = 0}\] , then what is the value of \[\mathbf{\overrightarrow a  \cdot \overrightarrow b  + \overrightarrow b  \cdot \overrightarrow c  + \overrightarrow c  \cdot \overrightarrow a }\] ?

Ans: Since \[\overrightarrow a \] , \[\overrightarrow b \] and \[\overrightarrow c \] are unit vectors, it means that \[|\overrightarrow a | = |\overrightarrow b | = |\overrightarrow c | = 1\] .

Further it is given that \[\overrightarrow a  + \overrightarrow b  + \overrightarrow c  = 0\] .

Squaring both sides:

\[ \Rightarrow {(\overrightarrow a  + \overrightarrow b  + \overrightarrow c )^2} = 0\]

\[ \Rightarrow |\overrightarrow a {|^2} + |\overrightarrow b {|^2} + |\overrightarrow c {|^2} + 2(\overrightarrow a  \cdot \overrightarrow b  + \overrightarrow b  \cdot \overrightarrow c  + \overrightarrow c  \cdot \overrightarrow a ) = 0\]

\[ \Rightarrow 1 + 1 + 1 + 2(\overrightarrow a  \cdot \overrightarrow b  + \overrightarrow b  \cdot \overrightarrow c  + \overrightarrow c  \cdot \overrightarrow a ) = 0\]

\[ \Rightarrow 2(\overrightarrow a  \cdot \overrightarrow b  + \overrightarrow b  \cdot \overrightarrow c  + \overrightarrow c  \cdot \overrightarrow a ) =  - 3\]

\[ \Rightarrow \overrightarrow a  \cdot \overrightarrow b  + \overrightarrow b  \cdot \overrightarrow c  + \overrightarrow c  \cdot \overrightarrow a  =  - \frac{3}{2}\]

26. If \[\mathbf{\overrightarrow a }\] and \[\mathbf{\overrightarrow b }\] are unit vectors such that \[\mathbf{\overrightarrow a  + 2\overrightarrow b} \] is perpendicular to \[\mathbf{5\overrightarrow a  - 4\overrightarrow b }\] , then what is the angle between \[\mathbf{\overrightarrow a }\] and \[\mathbf{\overrightarrow b }\] ?

Ans: It is given that \[\overrightarrow a \] and \[\overrightarrow b \] are unit vectors, and the vectors \[\overrightarrow a  + 2\overrightarrow b \] and \[5\overrightarrow a  - 4\overrightarrow b \] are perpendicular, that is, their dot product will be zero.

\[(\overrightarrow a  + 2\overrightarrow b ) \cdot (5\overrightarrow a  - 4\overrightarrow b ) = 0\]

\[ \Rightarrow 5|\overrightarrow a {|^2} + 6\overrightarrow a  \cdot \overrightarrow b  - 8|\overrightarrow b {|^2} = 0\]

\[ \Rightarrow 5{(1)^2} + 6\overrightarrow a  \cdot \overrightarrow b  - 8{(1)^2} = 0\] (Since \[\overrightarrow a \] and \[\overrightarrow b \] are unit vectors)

\[ \Rightarrow 6\overrightarrow a  \cdot \overrightarrow b  = 3\]

\[ \Rightarrow \overrightarrow a  \cdot \overrightarrow b  = \frac{1}{2}\]

Now, \[\overrightarrow a  \cdot \overrightarrow b  = |\overrightarrow a ||\overrightarrow b |\cos \theta \]

\[ \Rightarrow \frac{1}{2} = (1)(1)\cos \theta \]

\[ \Rightarrow \frac{1}{2} = \cos \theta \]

\[ \Rightarrow \theta  = \frac{\pi }{3}\]

Short Answer Questions (4 Mark)

27. If ABCDEF is a regular hexagon then using triangle law of addition prove that \[\mathbf{\overrightarrow {AB}  + \overrightarrow {AC}  + \overrightarrow {AD}  + \overrightarrow {AE}  + \overrightarrow {AF}  = 3\overrightarrow {AD}  = 6\overrightarrow {AO}} \] , O being the centre of hexagon.

Ans: ABCDEF is a regular polygon:

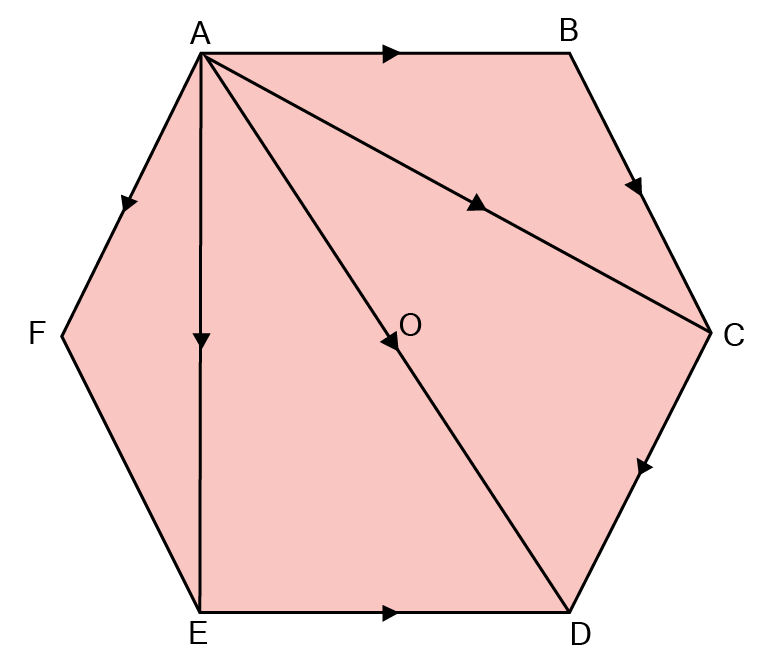
Hence, \[\overrightarrow {AB} ,\overrightarrow {BC} ,\overrightarrow {CD} ,\overrightarrow {ED} ,\overrightarrow {EF} ,\overrightarrow {AF} \] are all equal.

Further, using the triangle law of addition:

\[\overrightarrow {AC}  + \overrightarrow {CD}  = \overrightarrow {AD} \] ......(1)

And, \[\overrightarrow {AE}  + \overrightarrow {ED}  = \overrightarrow {AD} \] ......(2)

Now, taking (1)+(2) :

\[\overrightarrow {AC}  + \overrightarrow {CD}  + \overrightarrow {AE}  + \overrightarrow {ED}  = \overrightarrow {AD}  + \overrightarrow {AD} \]

Adding \[\overrightarrow {AD} \] both sides:

\[ \Rightarrow \overrightarrow {AC}  + \overrightarrow {CD}  + \overrightarrow {AE}  + \overrightarrow {ED}  + \overrightarrow {AD}  = 3\overrightarrow {AD} \]

\[ \Rightarrow \overrightarrow {AC}  + \overrightarrow {AF}  + \overrightarrow {AE}  + \overrightarrow {AB}  + \overrightarrow {AD}  = 3\overrightarrow {AD} \] (Since \[\overrightarrow {CD}  = \overrightarrow {AF} \] and \[\overrightarrow {AE}  = \overrightarrow {AB} \] )

Also, O is the midpoint of \[\overrightarrow {AD} \] , therefore, \[\overrightarrow {AD}  = 2\overrightarrow {AO} \] .

Hence, \[\overrightarrow {AC}  + \overrightarrow {AF}  + \overrightarrow {AE}  + \overrightarrow {AB}  + \overrightarrow {AD}  = 3\overrightarrow {AD}  = 6\overrightarrow {AO} \] is proved.

28. Points L, M, N divide the sides BC, CA, AB of a ABC in the ratios 1:4,3:2,3:7 respectively. Prove that \[\mathbf{\overrightarrow {AL}  + \overrightarrow {BM}  + \overrightarrow {CN} }\] is a vector parallel to \[\mathbf{\overrightarrow {CK} }\] where K divides AB in ratio 1:3 .

Ans: Let \[\overrightarrow a \] , \[\overrightarrow b \] and \[\overrightarrow c \] be the position vectors of points A, B and C respectively.

We find the position vectors of points L, M, N and K:

\[\overrightarrow {OL}  = \frac{{(1)\overrightarrow c  + (4)\vec b}}{{1 + 4}}\] (Since L divides BC in the ratio \[1:4\] )

\[ \Rightarrow \overrightarrow {OL}  = \frac{{\vec c + 4\vec b}}{5}\]

\[\overrightarrow {OM}  = \frac{{(3)\overrightarrow a  + (2)c}}{{3 + 2}}\] (Since M divides CA in the ratio \[3:2\] )

\[ \Rightarrow \overrightarrow {OM}  = \frac{{3\overrightarrow a  + 2\overrightarrow c }}{5}\]

\[\overrightarrow {ON}  = \frac{{(3)\overrightarrow b  + (7)\overrightarrow a }}{{3 + 7}}\] (Since N divides AB in the ratio \[3:7\] )

\[ \Rightarrow \overrightarrow {ON}  = \frac{{3\vec b + 7\vec a}}{{10}}\]

\[\overrightarrow {OK}  = \frac{{(1)\overrightarrow b  + (3)\overrightarrow a }}{{1 + 3}}\] (Since K divides AB in the ratio \[1:3\] )

\[ \Rightarrow \overrightarrow {OK}  = \frac{{\vec b + 3\vec a}}{4}\]

Taking \[\overrightarrow {AL}  + \overrightarrow {BM}  + \overrightarrow {CN} \] :

\[ = (\overrightarrow {OL}  - \overrightarrow {OA} ) + (\overrightarrow {BM}  - \overrightarrow {OB} ) + (\overrightarrow {CN}  - \overrightarrow {OC} )\]

\[ = (\overrightarrow {OL}  - \overrightarrow a ) + (\overrightarrow {OM}  - \overrightarrow b ) + (\overrightarrow {ON}  - \overrightarrow c )\]

\[ = (\frac{{\overrightarrow c  + 4\vec b}}{5} - \overrightarrow a ) + (\frac{{3\overrightarrow a  + 2\overrightarrow c }}{5} - \overrightarrow b ) + (\frac{{3\vec b + 7\overrightarrow a }}{{10}} - \overrightarrow c )\]

\[ = \frac{{2\overrightarrow c  + 8\vec b - 10\overrightarrow a  + 6\overrightarrow a  + 4\overrightarrow c  - 10\overrightarrow b  + 3\vec b + 7\overrightarrow a  - 10\overrightarrow c }}{{10}}\]

\[ = \frac{{3\overrightarrow a  + \overrightarrow b  - 4\overrightarrow c }}{{10}}\]

Now, \[\overrightarrow {CK}  = \overrightarrow {OK}  - \overrightarrow {OC} \]

\[ \Rightarrow \overrightarrow {CK}  = \frac{{\vec b + 3\vec a}}{4} - \overrightarrow c \]

\[ \Rightarrow \overrightarrow {CK}  = \frac{{\vec b + 3\vec a - 4\overrightarrow c }}{4}\] 

We notice that \[\overrightarrow {CK}  = \frac{5}{2} \times (\overrightarrow {AL}  + \overrightarrow {BM}  + \overrightarrow {CN} )\] .

Hence, we prove that \[\overrightarrow {AL}  + \overrightarrow {BM}  + \overrightarrow {CN} \] is parallel to \[\overrightarrow {CK} \] .

29. The scalar product of vector \[\mathbf{\hat i + \hat j + \hat k}\] with a unit vector along the sum of the vectors \[\mathbf{2\hat i + 4\hat j - 5\hat k}\] and \[\mathbf{\lambda \hat i + 2\hat j + 3\hat k}\] is equal to 1 . Find the value of \[\lambda \] .

Ans: The sum of vectors \[2\hat i + 4\hat j - 5\hat k\] and \[\lambda \hat i + 2\hat j + 3\hat k\] is:

\[(2\hat i + 4\hat j - 5\hat k) + (\lambda \hat i + 2\hat j + 3\hat k)\]

\[ = \hat i(2 + \lambda ) + \hat j(4 + 2) + \hat k( - 5 + 3)\]

\[ = (2 + \lambda )\hat i + 6\hat j - 2\hat k\]

The unit vector along the sum of \[2\hat i + 4\hat j - 5\hat k\] and \[\lambda \hat i + 2\hat j + 3\hat k\] vectors is:

\[\frac{{(2 + \lambda )\hat i + 6\hat j - 2\hat k}}{{|(2 + \lambda )\hat i + 6\hat j - 2\hat k|}}\]

\[ = \frac{{(2 + \lambda )\hat i + 6\hat j - 2\hat k}}{{\sqrt {{\lambda ^2} + 4\lambda  + 4 + 36 + 4} }}\]

\[ = \frac{{(2 + \lambda )\hat i + 6\hat j - 2\hat k}}{{\sqrt {{\lambda ^2} + 4\lambda  + 44} }}\]

The scalar product of \[\frac{{(2 + \lambda )\hat i + 6\hat j - 2\hat k}}{{\sqrt {{\lambda ^2} + 4\lambda  + 44} }}\] and \[\hat i + \hat j + \hat k\] is \[1\] .

Thus, \[(\frac{{(2 + \lambda )\hat i + 6\hat j - 2\hat k}}{{\sqrt {{\lambda ^2} + 4\lambda  + 44} }}) \cdot (\hat i + \hat j + \hat k) = 1\]

\[ \Rightarrow \frac{{(2 + \lambda ) + 6 - 2}}{{\sqrt {{\lambda ^2} + 4\lambda  + 44} }} = 1 \]

\[ \Rightarrow \lambda  + 6 = \sqrt {{\lambda ^2} + 4\lambda  + 44} \]

Squaring both sides:

\[ \Rightarrow {(\lambda  + 6)^2} = {\lambda ^2} + 4\lambda  + 44\]

\[ \Rightarrow {\lambda ^2} + 12\lambda  + 36 = {\lambda ^2} + 4\lambda  + 44\]

\[ \Rightarrow {\lambda ^2} + 12\lambda  + 36 = {\lambda ^2} + 4\lambda  + 44\]

\[ \Rightarrow 8\lambda  = 8\]

\[ \Rightarrow \lambda  = 1\]

30. \[\mathbf{\overrightarrow a} \] , \[\mathbf{\overrightarrow b }\] and \[\mathbf{\overrightarrow c }\] are three mutually perpendicular vectors of equal magnitude. Show that \[\mathbf{\overrightarrow a  + \overrightarrow b  + \overrightarrow c }\] makes equal angles with \[\mathbf{\overrightarrow a} \] , \[\mathbf{\overrightarrow b }\] and \[\mathbf{\overrightarrow c }\] with each angle as \[\mathbf{{\cos ^{ - 1}}\left( {\frac{1}{{\sqrt 3 }}} \right)}\] .

Ans: Let \[|\overrightarrow a | = |\overrightarrow b | = |\overrightarrow c | = \lambda \] and since they are mutually perpendicular, \[\overrightarrow a  \cdot \overrightarrow b  = \overrightarrow b  \cdot \overrightarrow c  = \overrightarrow a  \cdot \overrightarrow c  = 0\] .

Consider \[|\overrightarrow a  + \overrightarrow b  + \overrightarrow c {|^2}\] :

\[ \Rightarrow |\overrightarrow a  + \overrightarrow b  + \overrightarrow c {|^2} = |\overrightarrow a {|^2} + |\overrightarrow b {|^2} + |\overrightarrow c {|^2} + 2(\overrightarrow a  \cdot \overrightarrow b  + \overrightarrow b  \cdot \overrightarrow c  + \overrightarrow a  \cdot \overrightarrow c )\]

\[ \Rightarrow |\overrightarrow a  + \overrightarrow b  + \overrightarrow c {|^2} = {\lambda ^2} + {\lambda ^2} + {\lambda ^2} + 2(0 + 0 + 0)\] 

\[ \Rightarrow |\overrightarrow a  + \overrightarrow b  + \overrightarrow c {|^2} = 3{\lambda ^2}\]

\[ \Rightarrow |\overrightarrow a  + \overrightarrow b  + \overrightarrow c | = \sqrt 3 \lambda \]

Suppose \[\overrightarrow a ,\overrightarrow b ,\overrightarrow c \] make angles \[{\theta _1},{\theta _2},{\theta _3}\] with \[\overrightarrow a  + \overrightarrow b  + \overrightarrow c \] respectively.

Then, \[\cos {\theta _1} = \frac{{\overrightarrow a  \cdot (\overrightarrow a  + \overrightarrow b  + \overrightarrow c )}}{{|\overrightarrow a ||\overrightarrow a  + \overrightarrow b  + \overrightarrow c |}}\]

\[ \Rightarrow \cos {\theta _1} = \frac{{\overrightarrow a  \cdot \overrightarrow a  + \overrightarrow a  \cdot \overrightarrow b  + \overrightarrow a  \cdot \overrightarrow c }}{{|\overrightarrow a | \cdot \sqrt 3 \lambda }}\]

\[ \Rightarrow \cos {\theta _1} = \frac{{|\overrightarrow a {|^2}}}{{|\overrightarrow a | \cdot \sqrt 3 \lambda }}\]

\[ \Rightarrow \cos {\theta _1} = \frac{\lambda }{{\sqrt 3 \lambda }}\]

\[ \Rightarrow \cos {\theta _1} = \frac{1}{{\sqrt 3 }}\]

Similarly, \[\cos {\theta _2} = \cos {\theta _3} = \frac{1}{{\sqrt 3 }}\] .

Therefore, \[{\theta _1} = {\theta _2} = {\theta _3}\] .

31. If \[\mathbf{\overrightarrow \alpha   = 3\hat i - \hat j}\] and \[\mathbf{\overrightarrow \beta   = 2\hat i + \hat j + 3\hat k}\] then express \[\mathbf{\overrightarrow \beta } \] in the form of \[\mathbf{\overrightarrow \beta   = \overrightarrow {{\beta _1}}  + \overrightarrow {{\beta _2}} }\] , where \[\mathbf{\overrightarrow {{\beta _1}} }\] is parallel to \[\mathbf{\overrightarrow \alpha  }\] and \[\mathbf{\overrightarrow {{\beta _2}} }\] is perpendicular to \[\mathbf{\overrightarrow \alpha } \] .

Ans: It is given that \[\overrightarrow \alpha   = 3\hat i - \hat j\] and \[\overrightarrow \beta   = 2\hat i + \hat j + 3\hat k\] .

Since \[\vec \alpha \] is parallel to \[\overrightarrow {{\beta _1}} \] , that implies \[\overrightarrow {{\beta _1}}  = \lambda \overrightarrow \alpha  \] .

\[ \Rightarrow \overrightarrow {{\beta _1}}  = \lambda (3\hat i - \hat j)\]

Further, \[\overrightarrow \beta   = \overrightarrow {{\beta _1}}  + \overrightarrow {{\beta _2}} \]

\[ \Rightarrow 2\hat i + \hat j + 3\hat k = [\lambda (3\hat i - \hat j)] + \overrightarrow {{\beta _2}} \]

\[ \Rightarrow \overrightarrow {{\beta _2}}  = (2 - 3\lambda )\hat i + (1 + \lambda )\hat j + 3\hat k\]

Now, \[\overrightarrow {{\beta _2}} \] is perpendicular to \[\vec \alpha \] , hence their dot product will be equal to zero.

\[ \Rightarrow \overrightarrow \alpha   \cdot \overrightarrow {{\beta _2}}  = 0\]

\[ \Rightarrow (3\hat i - \hat j) \cdot [(2 - 3\lambda )\hat i + (1 + \lambda )\hat j + 3\hat k] = 0\]

\[ \Rightarrow 3(2 - 3\lambda ) + ( - 1 - \lambda ) = 0\]

\[ \Rightarrow 6 - 9\lambda  - 1 - \lambda  = 0\]

\[ \Rightarrow 5 - 10\lambda  = 0\]

\[ \Rightarrow \lambda  = \frac{1}{2}\]

We calculate the value of \[\overrightarrow {{\beta _1}} \] and \[\overrightarrow {{\beta _2}} \] :

\[\overrightarrow {{\beta _1}}  = \lambda (3\hat i - \hat j)\]

\[ \Rightarrow \overrightarrow {{\beta _1}}  = \frac{1}{2}(3\hat i - \hat j)\]

\[ \Rightarrow \overrightarrow {{\beta _1}}  = \frac{3}{2}\hat i - \frac{1}{2}\hat j\]

Also, \[\overrightarrow {{\beta _2}}  = (2 - 3\lambda )\hat i + (1 + \lambda )\hat j + 3\hat k\]

\[ \Rightarrow \overrightarrow {{\beta _2}}  = [2 - 3(\frac{1}{2})]\hat i + (1 + \frac{1}{2})\hat j + 3\hat k\]

\[ \Rightarrow \overrightarrow {{\beta _2}}  = \frac{1}{2}\hat i + \frac{3}{2}\hat j + 3\hat k\]

Hence, we can say \[\overrightarrow \beta   = \left( {\frac{3}{2}\hat i - \frac{1}{2}\hat j} \right) + \left( {\frac{1}{2}\hat i + \frac{3}{2}\hat j + 3\hat k} \right)\] .

32. If \[\mathbf{\overrightarrow a }\] , \[\mathbf{\overrightarrow b }\] , \[\mathbf{\overrightarrow c }\] are three vectors such that \[\mathbf{\overrightarrow a  + \overrightarrow b  + \overrightarrow c  = 0}\] then prove that \[\mathbf{\overrightarrow a  \times \overrightarrow b  = \overrightarrow b  \times \overrightarrow c  = \overrightarrow c  \times \overrightarrow a} \] .

Ans: We know that \[\overrightarrow a  + \overrightarrow b  + \overrightarrow c  = 0\] .

Cross multiplying both sides by \[\overrightarrow a \] :

\[\overrightarrow a  \times (\overrightarrow a  + \overrightarrow b  + \overrightarrow c ) = \overrightarrow a  \times \overrightarrow 0 \]

\[ \Rightarrow \overrightarrow a  \times \overrightarrow a  + \overrightarrow a  \times \overrightarrow b  + \overrightarrow a  \times \overrightarrow c  = 0\]

\[ \Rightarrow 0 + \overrightarrow a  \times \overrightarrow b  - \overrightarrow c  \times \overrightarrow a  = 0\] (Since \[\overrightarrow a  \times \overrightarrow a  = 0\] and \[\overrightarrow a  \times \overrightarrow c  =  - \overrightarrow c  \times \overrightarrow a \] )

\[ \Rightarrow \overrightarrow a  \times \overrightarrow b  = \overrightarrow c  \times \overrightarrow a \] ......(1)

Similarly, if we cross multiplying both sides of \[\overrightarrow a  + \overrightarrow b  + \overrightarrow c  = \overrightarrow 0 \] by \[\overrightarrow b \] :

\[\overrightarrow b  \times (\overrightarrow a  + \overrightarrow b  + \overrightarrow c ) = \overrightarrow b  \times \overrightarrow 0 \]

\[ \Rightarrow \overrightarrow b  \times \overrightarrow a  + \overrightarrow b  \times \overrightarrow b  + \overrightarrow b  \times \overrightarrow c  = 0\]

\[ \Rightarrow  - \overrightarrow a  \times \overrightarrow b  + \overrightarrow b  \times \overrightarrow c  = 0\] (Since \[\overrightarrow b  \times \overrightarrow b  = 0\] and \[\overrightarrow b  \times \overrightarrow a  =  - \overrightarrow a  \times \overrightarrow b \] )

\[ \Rightarrow \overrightarrow a  \times \overrightarrow b  = \overrightarrow b  \times \overrightarrow c \] ......(2)

From (1) and (2) , we conclude that \[\overrightarrow a  \times \overrightarrow b  = \overrightarrow b  \times \overrightarrow c  = \overrightarrow c  \times \overrightarrow a \] .

33. If \[\mathbf{|\overrightarrow a | = 3}\] , \[\mathbf{|\overrightarrow b | = 5}\] , \[\mathbf{|\overrightarrow c | = 7}\] and \[\mathbf{\overrightarrow a  + \overrightarrow b  + \overrightarrow c  = 0}\] , find the angle between \[\mathbf{\overrightarrow a} \] and \[\mathbf{\overrightarrow b} \] .

Ans: We know that \[\overrightarrow a  + \overrightarrow b  + \overrightarrow c  = 0\] .

\[ \Rightarrow \overrightarrow a  + \overrightarrow b  =  - \overrightarrow c \]

Squaring both sides:

\[ \Rightarrow {(\overrightarrow a  + \overrightarrow b )^2} = {( - \overrightarrow c )^2}\]

\[ \Rightarrow |\overrightarrow a {|^2} + |\overrightarrow b {|^2} + 2\overrightarrow a  \cdot \overrightarrow b  = | - \overrightarrow c {|^2}\]

\[ \Rightarrow {3^2} + {5^2} + 2\overrightarrow a  \cdot \overrightarrow b  = {( - 7)^2}\] (Since \[|\overrightarrow a | = 3\] , \[|\overrightarrow b | = 5\] , \[|\overrightarrow c | = 7\] )

\[ \Rightarrow 9 + 25 + 2\overrightarrow a  \cdot \overrightarrow b  = 49\]

\[ \Rightarrow 2\overrightarrow a  \cdot \overrightarrow b  = 15\]

\[ \Rightarrow 2(|\overrightarrow a ||\overrightarrow b |\cos \theta ) = 15\]

\[ \Rightarrow 2(3 \cdot 5 \cdot \cos \theta ) = 15\]

\[ \Rightarrow \cos \theta  = \frac{1}{2}\]

The angle between \[\overrightarrow a \] and \[\overrightarrow b \] is \[\frac{\pi }{3}\] .

34. Let \[\mathbf{\overrightarrow a  = \hat i - \hat j}\] , \[\mathbf{\overrightarrow b  = 3\hat j - \hat k}\] and \[\mathbf{\overrightarrow c  = 7\hat i - \hat k}\] , find a vector \[\mathbf{\overrightarrow d }\] which is perpendicular to \[\mathbf{\overrightarrow a} \] and \[\mathbf{\overrightarrow b }\] and \[\mathbf{\overrightarrow c  \cdot \overrightarrow d  = 1}\] .

Ans: It is given that \[\overrightarrow d \] is perpendicular to both \[\overrightarrow a \] and \[\overrightarrow b \] .

That implies \[\overrightarrow d  = \lambda (\overrightarrow a  \times \overrightarrow b )\] .

\[\overrightarrow d  = \lambda \left( {\begin{array}{*{20}{c}} {\hat i}&{\hat j}&{\hat k}\\ 1&{ - 1}&0\\ 0&3&{ - 1} \end{array}} \right)\]

\[ \Rightarrow \overrightarrow d  = \lambda [\hat i(1) - \hat j( - 1) + \hat k(3)]\]

\[ \Rightarrow \overrightarrow d  = \lambda (\hat i + \hat j + 3\hat k)\]

Also, \[\overrightarrow c  \cdot \overrightarrow d  = 1\] .

\[ \Rightarrow (7\hat i - \hat k) \cdot [\lambda (\hat i + \hat j + 3\hat k)] = 1\]

\[ \Rightarrow 7\lambda  + 0 - 3\lambda  = 1\]

\[ \Rightarrow 4\lambda  = 1\]

\[ \Rightarrow \lambda  = \frac{1}{4}\]

Hence, \[\overrightarrow d  = \frac{1}{4}(\hat i + \hat j + 3\hat k)\]

35. If \[\mathbf{\overrightarrow a  = \hat i + \hat j + \hat k}\] , \[\mathbf{\overrightarrow c  = \hat j - \hat k}\] are the given vectors then find a vector \[\mathbf{\overrightarrow b }\] satisfying the equation \[\mathbf{\overrightarrow a  \times \overrightarrow b  = \overrightarrow c }\] , \[\mathbf{\overrightarrow a  \cdot \overrightarrow b  = 3}\] .

Ans: Assume \[\overrightarrow b  = x\hat i + y\hat j + z\hat k\] .

Since \[\overrightarrow a  \cdot \overrightarrow b  = 3\] :

\[(\hat i + \hat j + \hat k) \cdot (x\hat i + y\hat j + z\hat k) = 3\]

\[ \Rightarrow x + y + z = 3\] ......(1)

Now, we have \[\overrightarrow a  \times \overrightarrow b  = \overrightarrow c \] :

\[ \Rightarrow (\hat i + \hat j + \hat k) \times (x\hat i + y\hat j + z\hat k) = \hat j - \hat k\]

\[ \Rightarrow \left( {\begin{array}{*{20}{c}} {\hat i}&{\hat j}&{\hat k}\\ 1&1&1\\ x&y&z \end{array}} \right) = \hat j - \hat k\]

\[ \Rightarrow \hat i(z - y) - \hat j(z - x) + \hat k(y - x) = \hat j - \hat k\]

On comparing, we find that \[z - y = 0\] , that is, \[y = z\] .

Further, \[ - z + x = 1\] , that is, \[x = 1 + z\] .

From (1) , we have:

\[x + y + z = 3\]

\[ \Rightarrow 1 + z + z + z = 3\] (Since \[y = z\] and \[x = 1 + z\] )

\[ \Rightarrow 3z = 2\]

\[ \Rightarrow z = \frac{2}{3}\]

\[ \Rightarrow y = \frac{2}{3}\]

\[ \Rightarrow x = \frac{5}{3}\]

Hence, \[\overrightarrow b  = \frac{{5\hat i + 2\hat j + 2\hat k}}{3}\] .

36. Find a unit vector perpendicular to plane ABC, when position vectors of A, B, C are \[\mathbf{3\hat i - \hat j + 2\hat k}\] , \[\mathbf{\hat i - \hat j - 3\hat k}\] and \[\mathbf{4\hat i - 3\hat j + \hat k}\] respectively.

Ans: We know that given any two vectors, their cross product will result in a vector that is perpendicular to the plane that the two vectors lie in.

Accordingly, we need to find a unit vector in the direction of \[\overrightarrow {AB}  \times \overrightarrow {AC} \] .

First, we find \[\overrightarrow {AB}  = \overrightarrow {OB}  - \overrightarrow {OA} \] :

\[\overrightarrow {AB}  = (\hat i - \hat j - 3\hat k) - (3\hat i - \hat j + 2\hat k)\]

\[ \Rightarrow \overrightarrow {AB}  =  - 2\hat i - 5\hat k\]

Next, \[\overrightarrow {AC}  = \overrightarrow {OC}  - \overrightarrow {OA} \] :

\[\overrightarrow {AC}  = (4\hat i - 3\hat j + \hat k) - (3\hat i - \hat j + 2\hat k)\]

\[ \Rightarrow \overrightarrow {AC}  = \hat i - 2\hat j - \hat k\]

Further, \[\overrightarrow {AB}  \times \overrightarrow {AC}  = \left( {\begin{array}{*{20}{c}} {\hat i}&{\hat j}&{\hat k}\\ { - 2}&0&{ - 5}\\ 1&{ - 2}&{ - 1} \end{array}} \right)\]

\[\overrightarrow {AB}  \times \overrightarrow {AC}  =  - 10\hat i - 7\hat j - 4\hat k\]

\[|\overrightarrow {AB}  \times \overrightarrow {AC} | = \sqrt {{{( - 10)}^2} + {{( - 7)}^2} + {{( - 4)}^2}} \]

\[|\overrightarrow {AB}  \times \overrightarrow {AC} | = \sqrt {100 + 49 + 16} \]

\[|\overrightarrow {AB}  \times \overrightarrow {AC} | = \sqrt {165} \]

Hence, required unit vector is \[\frac{{\overrightarrow {AB}  \times \overrightarrow {AC} }}{{|\overrightarrow {AB}  \times \overrightarrow {AC} |}} = \frac{{ - 10\hat i - 7\hat j - 4\hat k}}{{\sqrt {165} }}\] .

37. For any two vectors, show that \[\mathbf{|\overrightarrow a  + \overrightarrow b | \le |\overrightarrow a | + |\overrightarrow b |}\] .

Ans: We take the square of \[\overrightarrow a  + \overrightarrow b \] :

\[{\left( {\overrightarrow a  + \overrightarrow b } \right)^2} = \overrightarrow a  \cdot \overrightarrow a  + \overrightarrow b  \cdot \overrightarrow a  + \overrightarrow a  \cdot \overrightarrow b  + \overrightarrow b  \cdot \overrightarrow b \]

\[ \Rightarrow {\left( {\overrightarrow a  + \overrightarrow b } \right)^2} = |\overrightarrow a {|^2} + 2\overrightarrow a  \cdot \overrightarrow b  + |\overrightarrow b {|^2}\]

\[ \Rightarrow {\left( {\overrightarrow a  + \overrightarrow b } \right)^2} = |\overrightarrow a {|^2} + 2\overrightarrow a  \cdot \overrightarrow b \cos \theta  + |\overrightarrow b {|^2}\]  ......(1)

We know that \[\cos \theta  \le 1\] .

Multiplying \[2\overrightarrow a  \cdot \overrightarrow b \] both sides:

\[2\overrightarrow a  \cdot \overrightarrow b \cos \theta  \le 2\overrightarrow a  \cdot \overrightarrow b \]

Adding \[|\overrightarrow a {|^2} + |\overrightarrow b {|^2}\] both sides:

\[|\overrightarrow a {|^2} + |\overrightarrow b {|^2} + 2\overrightarrow a  \cdot \overrightarrow b \cos \theta  \le |\overrightarrow a {|^2} + |\overrightarrow b {|^2} + 2\overrightarrow a  \cdot \overrightarrow b \]

\[ \Rightarrow |\overrightarrow a  + \overrightarrow b {|^2} \le {\left( {|\overrightarrow a | + |\overrightarrow b |} \right)^2}\] (From (1)) 

Hence proved, \[|\overrightarrow a  + \overrightarrow b {|^2} \le {\left( {|\overrightarrow a | + |\overrightarrow b |} \right)^2}\] .

38. Evaluate \[\mathbf{{\left( {\overrightarrow a  \times \hat i} \right)^2} + {\left( {\overrightarrow a  \times \hat j} \right)^2} + {\left( {\overrightarrow a  \times \hat k} \right)^2}}\] .

Ans: Let \[\overrightarrow a  = x\hat i + y\hat j + z\hat k\] .

So, \[\overrightarrow a  \times \hat i =  - y\hat k + z\hat j\]

\[\overrightarrow a  \times \hat j = x\hat k - z\hat i\]

\[\overrightarrow a  \times \hat k =  - x\hat j + y\hat i\]

Now, \[{\left( {\overrightarrow a  \times \hat i} \right)^2} + {\left( {\overrightarrow a  \times \hat j} \right)^2} + {\left( {\overrightarrow a  \times \hat k} \right)^2}\]

\[ \Rightarrow {y^2} + {z^2} + {x^2} + {z^2} + {x^2} + {y^2}\]

\[ \Rightarrow 2({x^2} + {y^2} + {z^2})\]

\[ \Rightarrow 2|\overrightarrow a {|^2}\]

Hence, \[{\left( {\overrightarrow a  \times \hat i} \right)^2} + {\left( {\overrightarrow a  \times \hat j} \right)^2} + {\left( {\overrightarrow a  \times \hat k} \right)^2} = 2|\overrightarrow a {|^2}\] .

39. If \[\mathbf{\hat a}\] and \[\mathbf{\hat b}\] are unit vectors inclined at an angle \[\mathbf{\theta} \] then prove that:

i. \[\mathbf{\sin \frac{\theta }{2} = \frac{1}{2}\left| {\hat a - \hat b} \right|}\]

Ans: Taking \[|\hat a - \hat b{|^2} = \hat a \cdot \hat a + \hat b \cdot \hat b - 2\hat a \cdot \hat b\] :

\[ \Rightarrow |\hat a - \hat b{|^2} = |\hat a{|^2} + |\hat b{|^2} - 2|\hat a||\hat b|\cos \theta \]

\[ \Rightarrow |\hat a - \hat b{|^2} = 1 + 1 - 2(1)(1)\cos \theta \] (Since they are unit vectors, their magnitude is equal to one)

\[ \Rightarrow |\hat a - \hat b{|^2} = 2(1 - \cos \theta )\]

\[ \Rightarrow \frac{{|\hat a - \hat b{|^2}}}{2} = 1 - \cos \theta \]

\[ \Rightarrow \frac{{|\hat a - \hat b{|^2}}}{2} = 2{\sin ^2}\frac{\theta }{2}\]

\[ \Rightarrow \frac{{|\hat a - \hat b{|^2}}}{4} = {\sin ^2}\frac{\theta }{2}\]

\[ \Rightarrow \frac{{|\hat a - \hat b|}}{2} = \sin \frac{\theta }{2}\] ......(1)

Hence proved.

ii. \[\mathbf{\tan \frac{\theta }{2} = \left| {\frac{{\hat a - \hat b}}{{\hat a + \hat b}}} \right|}\]

Ans: Taking \[|\hat a + \hat b{|^2} = \hat a \cdot \hat a + \hat b \cdot \hat b + 2\hat a \cdot \hat b\] :

\[ \Rightarrow |\hat a + \hat b{|^2} = |\hat a{|^2} + |\hat b{|^2} + 2|\hat a||\hat b|\cos \theta \]

\[ \Rightarrow |\hat a + \hat b{|^2} = 1 + 1 + 2(1)(1)\cos \theta \] (Since they are unit vectors, their magnitude is equal to one)

\[ \Rightarrow |\hat a + \hat b{|^2} = 2(1 + \cos \theta )\]

\[ \Rightarrow \frac{{|\hat a + \hat b{|^2}}}{2} = 1 + \cos \theta \]

\[ \Rightarrow \frac{{|\hat a + \hat b{|^2}}}{2} = 2{\cos ^2}\frac{\theta }{2}\]

\[ \Rightarrow \frac{{|\hat a + \hat b{|^2}}}{4} = {\cos ^2}\frac{\theta }{2}\]

\[ \Rightarrow \frac{{|\hat a + \hat b|}}{2} = \cos \frac{\theta }{2}\] ......(2)

We know that \[\tan \frac{\theta }{2} = \frac{{\sin \frac{\theta }{2}}}{{\cos \frac{\theta }{2}}}\]

From (1) and (2) :

\[\tan \frac{\theta }{2} = \frac{{\frac{{|\hat a - \hat b|}}{2}}}{{\frac{{|\hat a + \hat b|}}{2}}}\]

\[\tan \frac{\theta }{2} = \left| {\frac{{\hat a - \hat b}}{{\hat a + \hat b}}} \right|\]

Hence proved. 

40. For any two vectors, show that \[\mathbf{|\overrightarrow a  \times \overrightarrow b | = \sqrt {{a^2}{b^2} - {{(\overrightarrow a  \cdot \overrightarrow b )}^2}} }\] .

Ans: Taking \[|\overrightarrow a  \times \overrightarrow b {|^2}\] :

\[|\overrightarrow a  \times \overrightarrow b {|^2} = {\left( {|\overrightarrow a ||\overrightarrow b |\sin \theta } \right)^2}\]

\[ \Rightarrow |\overrightarrow a  \times \overrightarrow b {|^2} = |\overrightarrow a {|^2}|\overrightarrow b {|^2}{\sin ^2}\theta \]

\[ \Rightarrow |\overrightarrow a  \times \overrightarrow b {|^2} = |\overrightarrow a {|^2}|\overrightarrow b {|^2}(1 - {\cos ^2}\theta )\]

\[ \Rightarrow |\overrightarrow a  \times \overrightarrow b {|^2} = |\overrightarrow a {|^2}|\overrightarrow b {|^2} - |\overrightarrow a {|^2}|\overrightarrow b {|^2}{\cos ^2}\theta \]

\[ \Rightarrow |\overrightarrow a  \times \overrightarrow b {|^2} = |\overrightarrow a {|^2}|\overrightarrow b {|^2} - {(\overrightarrow a  \cdot \overrightarrow b )^2}\]

\[ \Rightarrow |\overrightarrow a  \times \overrightarrow b | = \sqrt {|\overrightarrow a {|^2}|\overrightarrow b {|^2} - {{(\overrightarrow a  \cdot \overrightarrow b )}^2}} \]

Hence proved.

41. \[\mathbf{\overrightarrow a  = \hat i + \hat j + \hat k}\] , \[\mathbf{\overrightarrow b  = \hat i - \hat j + 2\hat k}\] and \[\mathbf{\overrightarrow c  = x\hat i + (x - 2)\hat j - \hat k}\] . If \[\mathbf{\overrightarrow c }\] lies in the plane of \[\mathbf{\overrightarrow a }\] and \[\mathbf{\overrightarrow b }\] , then find the value of x .

Ans: We have \[\overrightarrow a  = \hat i + \hat j + \hat k\] , \[\overrightarrow b  = \hat i - \hat j + 2\hat k\] and \[\overrightarrow c  = x\hat i + (x - 2)\hat j - \hat k\] .

Since vectors \[\overrightarrow a ,\overrightarrow b ,\overrightarrow c \] are co-planar, that is, lying on the same plane, hence their scalar product will be equal to zero. 

\[ \Rightarrow [\overrightarrow a  \cdot \overrightarrow b  \cdot \overrightarrow c ] = 0\]

\[ \Rightarrow \left| {\begin{array}{*{20}{c}} 1&1&1\\ 1&{ - 1}&2\\ x&{x - 2}&{ - 1} \end{array}} \right| = 0\]

\[ \Rightarrow 1(1 - 2x + 4) - 1( - 1 - 2x) + 1(x - 2 + x) = 0\]

\[ \Rightarrow 5 - 2x + 1 + 2x - 2 + 2x = 0\]

\[ \Rightarrow 4 + 2x = 0\]

\[ \Rightarrow x =  - 2\]

42. Prove that the angle between any two diagonals of a cube is \[\mathbf{{\cos ^{ - 1}}\left( {\frac{1}{3}} \right)}\] .

Ans: Let us first graphically represent a cube to prove the required:

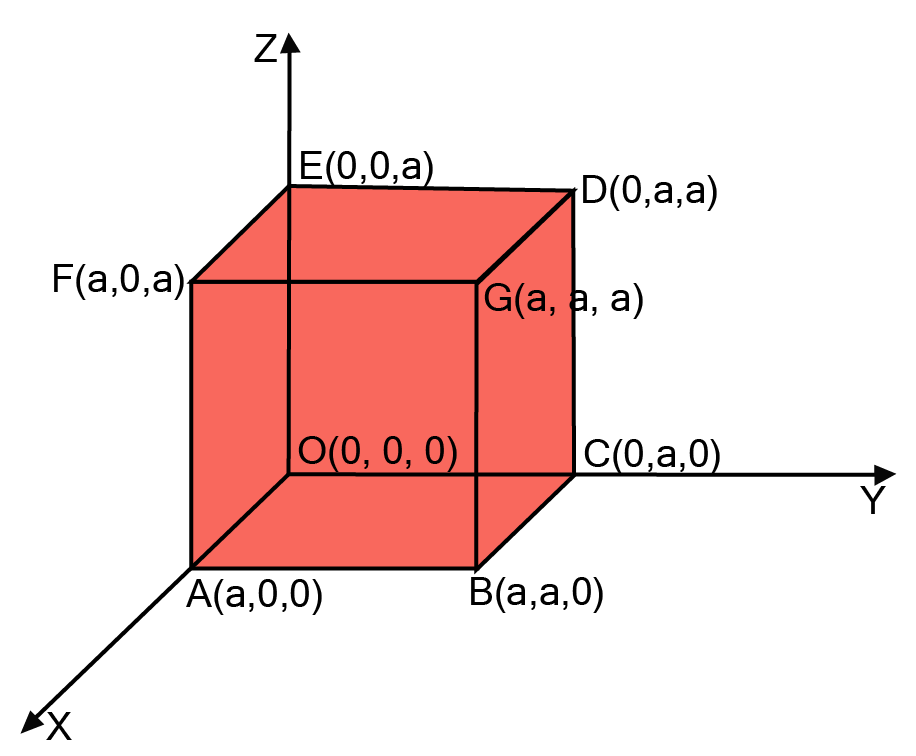
Let a be the edge of the cube with its centre \[O\] at the origin. The diagonals of this cube are AD, OG, BE and CF. 

Let us consider the diagonals AD and OG. 

\[\overrightarrow {OG}  = a\hat i + a\hat j + a\hat k\]

\[\overrightarrow {AD}  = \overrightarrow {OD}  - \overrightarrow {OA} \]

\[ \Rightarrow \overrightarrow {AD}  = (0 - a)\hat i + (a - 0)\hat j + (a - 0)\hat k\]

\[ \Rightarrow \overrightarrow {AD}  =  - a\hat i + a\hat j + a\hat k\]

Now, let the angle between them be \[\theta \] :

\[\cos \theta  = \frac{{\overrightarrow {AD}  \cdot \overrightarrow {OG} }}{{|\overrightarrow {AD} ||\overrightarrow {OG} |}}\]

\[ \Rightarrow \cos \theta  = \frac{{a( - a) + a(a) + a(a)}}{{\sqrt {{a^2} + {a^2} + {a^2}} \sqrt {{{( - a)}^2} + {a^2} + {a^2}} }}\]

\[ \Rightarrow \cos \theta  = \frac{{ - {a^2} + {a^2} + {a^2}}}{{\sqrt {3{a^2}} \sqrt {3{a^2}} }}\]

\[ \Rightarrow \cos \theta  = \frac{{{a^2}}}{{3{a^2}}}\]

\[ \Rightarrow \cos \theta  = \frac{1}{3}\]

\[ \Rightarrow \theta  = {\cos ^{ - 1}}\left( {\frac{1}{3}} \right)\]

Similarly, the angle between BE and CF will also be \[{\cos ^{ - 1}}\left( {\frac{1}{3}} \right)\] .

Hence proved.

43. Let \[\mathbf{\hat a,\hat b,\hat c}\] are unit vectors such that \[\mathbf{\hat a \cdot \hat b{\rm{ = }}\hat a \cdot \hat c = 0}\]and the angle between \[\mathbf{\hat b}\] and \[\mathbf{\hat c}\] is \[\mathbf{\frac{\pi }{6}}\] , then prove that \[\mathbf{\hat a =  \pm 2(\hat b \times \hat c)}\] .

Ans: Since \[\hat a \cdot \hat b{\rm{ = }}\hat a \cdot \hat c = 0\] , it means that \[\hat a\] is perpendicular to both \[\hat b\] and \[\hat c\] .

This further implies that \[\hat a\] is perpendicular to the plane in which \[\hat b\] and \[\hat c\] lie.

Also, \[\hat b \times \hat c = |\hat b||\hat c|\sin \theta \hat n\]  , where \[\theta \] is the angle between \[\hat b\] and \[\hat c\] , and \[\hat n\] is a unit vector perpendicular to the plane in which \[\hat b\] and \[\hat c\] lie.

\[ \Rightarrow \hat b \times \hat c = (1)(1)\sin \frac{\pi }{6}\hat a\]

(Since \[\hat b\] and \[\hat c\] are unit vectors, the angle between them is given to be \[\frac{\pi }{6}\] , and \[\hat a\] satisfies the conditions for \[\hat n\] )

\[ \Rightarrow \hat b \times \hat c = \sin \frac{\pi }{6}\hat a\]

\[ \Rightarrow \hat b \times \hat c = \frac{1}{2}\hat a\]

\[ \Rightarrow \hat a =  \pm 2(\hat b \times \hat c)\]

Hence proved.

44. Prove that the normal vector to the plane containing three points with

position vectors \[\overrightarrow a \] , \[\overrightarrow b \] and \[\overrightarrow c \] lies in the direction of vector \[\overrightarrow b  \times \overrightarrow c  + \overrightarrow c  \times \overrightarrow a  + \overrightarrow a  \times \overrightarrow b \] .

Ans: In a plane containing the vectors \[\overrightarrow a \] , \[\overrightarrow b \] and \[\overrightarrow c \] , let \[\overrightarrow n \] be its normal vector.

Therefore, \[\overrightarrow n  = \lambda (\overrightarrow {AB}  \times \overrightarrow {AC} )\] .

\[ \Rightarrow \overrightarrow n  = \lambda [(\overrightarrow b  - \overrightarrow a ) \times (\overrightarrow c  - \overrightarrow a )]\]

\[ \Rightarrow \overrightarrow n  = \lambda [(\overrightarrow b  - \overrightarrow a ) \times \overrightarrow c  - (\overrightarrow b  - \overrightarrow a ) \times \overrightarrow a ]\] (By distributive property)

\[ \Rightarrow \overrightarrow n  = \lambda (\overrightarrow b  \times \overrightarrow c  - \overrightarrow a  \times \overrightarrow c  - \overrightarrow b  \times \overrightarrow a  + \overrightarrow a  \times \overrightarrow a )\]

\[ \Rightarrow \overrightarrow n  = \lambda (\overrightarrow b  \times \overrightarrow c  + \overrightarrow c  \times \overrightarrow a  + \overrightarrow a  \times \overrightarrow b  + 0)\] (Since \[\overrightarrow a  \times \overrightarrow a  = 0\] , \[\overrightarrow a  \times \overrightarrow c  =  - \overrightarrow c  \times \overrightarrow a \] , \[\overrightarrow b  \times \overrightarrow a  =  - \overrightarrow a  \times \overrightarrow b \] )

\[ \Rightarrow \overrightarrow n  = \lambda (\overrightarrow b  \times \overrightarrow c  + \overrightarrow c  \times \overrightarrow a  + \overrightarrow a  \times \overrightarrow b )\]

Hence, we can say that \[\overrightarrow n \] lies in the direction of \[\overrightarrow b  \times \overrightarrow c  + \overrightarrow c  \times \overrightarrow a  + \overrightarrow a  \times \overrightarrow b \] .

45. If \[\mathbf{\overrightarrow a }\] , \[\mathbf{\overrightarrow b }\] and \[\mathbf{\overrightarrow c }\] are position vectors of the vertices A, B and C of a triangle ABC, then show that the area of ABC is \[\mathbf{\frac{1}{2}\left| {\overrightarrow a  \times \overrightarrow b  + \overrightarrow b  \times \overrightarrow c  + \overrightarrow c  \times \overrightarrow a } \right|}\] .

Ans: Let us consider a parallelogram ABCD:

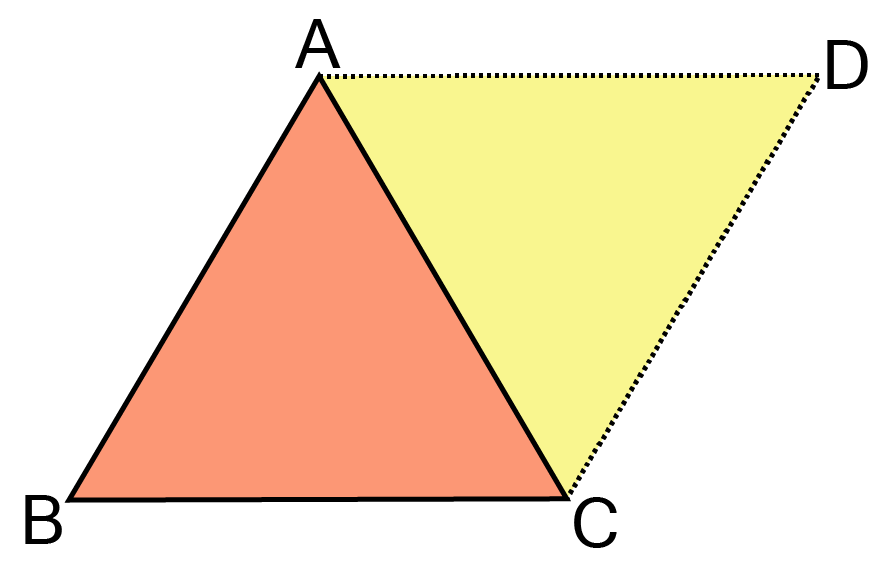
Area of ABCD will be \[\overrightarrow {AB}  \times \overrightarrow {AC} \] , that is, the product of two adjacent vectors.

Hence, area of \[ABC\] will be \[\frac{1}{2}\left( {\overrightarrow {AB}  \times \overrightarrow {AC} } \right)\] .

\[ \Rightarrow \frac{1}{2}\left( {(\overrightarrow b  - \overrightarrow a ) \times (\overrightarrow c  - \overrightarrow a )} \right)\]

\[ \Rightarrow \frac{1}{2}\left( {(\overrightarrow b  - \overrightarrow a ) \times \overrightarrow c  - (\overrightarrow b  - \overrightarrow a ) \times \overrightarrow a } \right)\]

\[ \Rightarrow \frac{1}{2}\left( {\overrightarrow b  \times \overrightarrow c  - \overrightarrow a  \times \overrightarrow c  - \overrightarrow b  \times \overrightarrow a  + \overrightarrow a  \times \overrightarrow a } \right)\]

\[ \Rightarrow \frac{1}{2}\left( {\overrightarrow b  \times \overrightarrow c  + \overrightarrow c  \times \overrightarrow a  + \overrightarrow a  \times \overrightarrow b  + 0} \right)\] (Since \[\overrightarrow a  \times \overrightarrow a  = 0\] , \[\overrightarrow a  \times \overrightarrow c  =  - \overrightarrow c  \times \overrightarrow a \] , \[\overrightarrow b  \times \overrightarrow a  =  - \overrightarrow a  \times \overrightarrow b \] )

\[ \Rightarrow \frac{1}{2}\left( {\overrightarrow b  \times \overrightarrow c  + \overrightarrow c  \times \overrightarrow a  + \overrightarrow a  \times \overrightarrow b } \right)\]

Hence proved.

46. If \[\mathbf{\overrightarrow a  \times \overrightarrow b  = \overrightarrow c  \times \overrightarrow d }\] and \[\mathbf{\overrightarrow a  \times \overrightarrow c  = \overrightarrow b  \times \overrightarrow d} \] , then prove that \[\mathbf{\overrightarrow a  - \overrightarrow d} \] is parallel to \[\mathbf{\overrightarrow b  - \overrightarrow c} \] provided \[\mathbf{\overrightarrow a  \ne \overrightarrow d }\] and \[\mathbf{\overrightarrow b  \ne \overrightarrow c }\] .

Ans: For vectors \[\overrightarrow a  - \overrightarrow d \] and \[\overrightarrow b  - \overrightarrow c \] to be parallel, their cross product must be equal to zero.

\[ \Rightarrow \left( {\overrightarrow a  - \overrightarrow d } \right) \times \left( {\overrightarrow b  - \overrightarrow c } \right) \]

\[ \Rightarrow (\overrightarrow a  - \overrightarrow d ) \times \overrightarrow b  - (\overrightarrow a  - \overrightarrow d ) \times \overrightarrow c \]

\[ \Rightarrow \overrightarrow a  \times \overrightarrow b  - \overrightarrow d  \times \overrightarrow b  - \overrightarrow a  \times \overrightarrow c  + \overrightarrow d  \times \overrightarrow c \]

\[ \Rightarrow \overrightarrow a  \times \overrightarrow b  + \overrightarrow b  \times \overrightarrow d  - \overrightarrow a  \times \overrightarrow c  - \overrightarrow c  \times \overrightarrow d \] (Since \[ - \overrightarrow d  \times \overrightarrow b  = \overrightarrow b  \times \overrightarrow d \] and \[\overrightarrow d  \times \overrightarrow c  =  - \overrightarrow c  \times \overrightarrow d \] )

\[ \Rightarrow 0\] (Since \[\overrightarrow a  \times \overrightarrow b  = \overrightarrow c  \times \overrightarrow d \] and \[\overrightarrow a  \times \overrightarrow c  = \overrightarrow b  \times \overrightarrow d \] )

Hence proved.

47. Dot product of a vector with vectors \[\mathbf{\hat i + \hat j - 3\hat k}\] , \[\mathbf{\hat i + 3\hat j - 2\hat k}\] and \[\mathbf{2\hat i + \hat j + 4\hat k}\] is 0 , 5 and 8 respectively. Find the vector.

Ans: Let the required vector be \[\overrightarrow h  = x\hat i + y\hat j + z\hat k\] . We have given \[\overrightarrow a  = \hat i + \hat j - 3\hat k\] , \[\overrightarrow b  = \hat i + 3\hat j - 2\hat k\] , \[\overrightarrow c  = 2\hat i + \hat j + 4\hat k\] and \[\overrightarrow a  \cdot \overrightarrow h  = 0\] , \[\overrightarrow b  \cdot \overrightarrow h  = 5\] , \[\overrightarrow c  \cdot \overrightarrow h  = 8\] .

Since \[\overrightarrow a  \cdot \overrightarrow h  = 0\] :

\[(\hat i + \hat j - 3\hat k) \cdot (x\hat i + y\hat j + z\hat k) = 0\]

\[ \Rightarrow x + y - 3z = 0\] ......(1)

Since \[\overrightarrow b  \cdot \overrightarrow h  = 5\] :

\[(\hat i + 3\hat j - 2\hat k) \cdot (x\hat i + y\hat j + z\hat k) = 5\]

\[ \Rightarrow x + 3y - 2z = 5\] ......(2)

Since \[\overrightarrow c  \cdot \overrightarrow h  = 8\] :

\[(2\hat i + \hat j + 4\hat k) \cdot (x\hat i + y\hat j + z\hat k) = 8\]

\[ \Rightarrow 2x + y + 4z = 8\] ......(3)

Subtract equation (1) from (2) :

\[\left( {x + 3y - 2z} \right) - \left( {x + y - 3z} \right) = 5\]

\[ \Rightarrow 2y + z = 5\]

\[ \Rightarrow y = \frac{{5 - z}}{2}\]

Subtract equation (1) from (3) :

\[\left( {2x + y + 4z} \right) - \left( {x + y - 3z} \right) = 8\]

\[ \Rightarrow x + 7z = 8\]

\[ \Rightarrow x = 8 - 7z\]

Substituting in (1) :

\[x + y - 3z = 0\]

\[ \Rightarrow 8 - 7z + \frac{{5 - z}}{2} - 3z = 0\]

\[ \Rightarrow 8 - 10z + \frac{{5 - z}}{2} = 0\]

\[ \Rightarrow \frac{{16 - 20z + 5 - z}}{2} = 0\]

\[ \Rightarrow \frac{{21 - 21z}}{2} = 0\]

\[ \Rightarrow 21 - 21z = 0\]

\[ \Rightarrow z = 1\]

Now, \[x = 8 - 7(1)\]

\[ \Rightarrow x = 1\]

Also, \[y = \frac{{5 - 1}}{2}\]

\[ \Rightarrow y = 2\]

Hence, we have \[\overrightarrow h  = \hat i + 2\hat j + \hat k\] .

48. If \[\mathbf{\overrightarrow a  = 5\hat i - \hat j + 7\hat k}\] , \[\mathbf{\hat b = \hat i - \hat j - \lambda \hat k}\] , find \[\mathbf{\lambda} \] such that \[\mathbf{\overrightarrow a  + \overrightarrow b} \] and \[\mathbf{\overrightarrow a  - \overrightarrow b }\] are orthogonal. 

Ans: If \[\overrightarrow a  + \overrightarrow b \] and \[\overrightarrow a  - \overrightarrow b \] are orthogonal, it implies that their dot product is zero.

We find \[\overrightarrow a  + \overrightarrow b \] :

\[\overrightarrow a  + \overrightarrow b  = (5\hat i - \hat j + 7\hat k) + (\hat i - \hat j - \lambda \hat k)\]

\[ \Rightarrow \overrightarrow a  + \overrightarrow b  = 6\hat i - 2\hat j + (7 - \lambda )\hat k\]

Similarly, we find \[\overrightarrow a  - \overrightarrow b \] :

\[\overrightarrow a  - \overrightarrow b  = (5\hat i - \hat j + 7\hat k) - (\hat i - \hat j - \lambda \hat k)\]

\[ \Rightarrow \overrightarrow a  - \overrightarrow b  = 4\hat i + (7 + \lambda )\hat k\]

Now, \[(\overrightarrow a  + \overrightarrow b ) \cdot (\overrightarrow a  - \overrightarrow b ) = 0\] :

\[ \Rightarrow [6\hat i - 2\hat j + (7 - \lambda )\hat k] \cdot [4\hat i + (7 + \lambda )\hat k] = 0\]

\[ \Rightarrow 24 + 0 + 49 - {\lambda ^2} = 0\]

\[ \Rightarrow {\lambda ^2} = 73\]

\[ \Rightarrow \lambda  = \sqrt {73} \]

49. Let \[\mathbf{\overrightarrow a }\] and \[\mathbf{\overrightarrow b }\] be vectors such that \[\mathbf{|\overrightarrow a | = |\overrightarrow b | = |\overrightarrow a  - \overrightarrow b | = 1}\] , then find \[\mathbf{|\overrightarrow a  + \overrightarrow b |}\] .

Ans: Let us take \[|\overrightarrow a  - \overrightarrow b | = 1\] and square both sides:

\[ \Rightarrow |\overrightarrow a  - \overrightarrow b {|^2} = {1^2}\]

\[ \Rightarrow |\overrightarrow a {|^2} + |\overrightarrow b {|^2} - 2\overrightarrow a  \cdot \overrightarrow b  = 1\]

\[ \Rightarrow 1 + 1 - 2(|\overrightarrow a ||\overrightarrow b |\cos \theta ) = 1\] (Since \[|\overrightarrow a | = |\overrightarrow b | = 1\] )

\[ \Rightarrow 2 - 2\cos \theta  = 1\]

\[ \Rightarrow 2\cos \theta  = 1\]

\[ \Rightarrow \cos \theta  = \frac{1}{2}\]

Now, let us take \[|\overrightarrow a  + \overrightarrow b |\]:

\[ \Rightarrow \sqrt {|\overrightarrow a {|^2} + |\overrightarrow b {|^2} + 2\overrightarrow a  \cdot \overrightarrow b } \]

\[ \Rightarrow \sqrt {1 + 1 + 2(|\overrightarrow a ||\overrightarrow b |\cos \theta )} \] (Since \[|\overrightarrow a | = |\overrightarrow b | = 1\] )

\[ \Rightarrow \sqrt {2 + 2(\frac{1}{2})} \]

\[ \Rightarrow \sqrt {2 + 1} \]

\[ \Rightarrow \sqrt 3 \]

50. If \[\mathbf{|\overrightarrow a | = 2}\] , \[\mathbf{|\overrightarrow b | = 5}\] and \[\mathbf{\overrightarrow a  \times \overrightarrow b  = 2\hat i + \hat j - 2\hat k}\] , find the value of \[\mathbf{\overrightarrow a  \cdot \overrightarrow b} \] .

Ans: Let us find \[|\overrightarrow a  \times \overrightarrow b |\] , given that \[\overrightarrow a  \times \overrightarrow b  = 2\hat i + \hat j - 2\hat k\] : 

\[ \Rightarrow |\overrightarrow a  \times \overrightarrow b | = \sqrt {{2^2} + {1^2} + {{( - 2)}^2}} \]

\[ \Rightarrow |\overrightarrow a  \times \overrightarrow b | = \sqrt 9 \]

\[ \Rightarrow |\overrightarrow a  \times \overrightarrow b | = 3\]

Now, \[|\overrightarrow a  \times \overrightarrow b | = |\overrightarrow a ||\overrightarrow b |\sin \theta \]

\[ \Rightarrow 3 = (2)(5)\sin \theta \]

\[ \Rightarrow \sin \theta  = \frac{3}{{10}}\]

Now, \[\overrightarrow a  \cdot \overrightarrow b  = |\overrightarrow a ||\overrightarrow b |\cos \theta \] :

\[ \Rightarrow \overrightarrow a  \cdot \overrightarrow b  = (2)(5)\cos ({\sin ^{ - 1}}\frac{3}{{10}})\]

\[ \Rightarrow \overrightarrow a  \cdot \overrightarrow b  = (2)(5)\cos ({\sin ^{ - 1}}\frac{3}{{10}})\]

\[ \Rightarrow \overrightarrow a  \cdot \overrightarrow b  = 10\cos ({\cos ^{ - 1}}\sqrt {1 - {{\left( {\frac{3}{{10}}} \right)}^2}} )\] (Since \[{\sin ^{ - 1}}x = {\cos ^{ - 1}}\sqrt {1 - {x^2}} \] )

\[ \Rightarrow \overrightarrow a  \cdot \overrightarrow b  = 10\sqrt {\frac{{91}}{{100}}} \]

\[ \Rightarrow \overrightarrow a  \cdot \overrightarrow b  = \sqrt {91} \]

51. \[\mathbf{\overrightarrow a ,\overrightarrow b ,\overrightarrow c }\] are three vectors such that \[\mathbf{\overrightarrow b  \times \overrightarrow c  = \overrightarrow a }\] and \[\mathbf{\overrightarrow a  \times \overrightarrow b  = \overrightarrow c} \] . Prove that \[\mathbf{\overrightarrow a ,\overrightarrow b ,\overrightarrow c }\] are mutually perpendicular to each other and \[\mathbf{|\overrightarrow b | = 1}\] , \[\mathbf{|\overrightarrow c | = |\overrightarrow a |}\] .

Ans: We know that \[\overrightarrow b  \times \overrightarrow c  = \overrightarrow a \] and \[\overrightarrow a  \times \overrightarrow b  = \overrightarrow c \] .

Since \[\overrightarrow b  \times \overrightarrow c  = \overrightarrow a \] , we can say that \[\overrightarrow b  \bot \overrightarrow a \] and \[\overrightarrow c  \bot \overrightarrow a \] .

Similarly, since \[\overrightarrow a  \times \overrightarrow b  = \overrightarrow c \] , we conclude that \[\overrightarrow a  \bot \overrightarrow c \] and \[\overrightarrow b  \bot \overrightarrow c \] .

From above statements, we can observe that \[\overrightarrow a  \bot \overrightarrow b \] , \[\overrightarrow b  \bot \overrightarrow c \] , \[\overrightarrow a  \bot \overrightarrow c \] , that is, all three vectors are mutually perpendicular.

Now, we have \[\overrightarrow a  \times \overrightarrow b  = \overrightarrow c \] .

\[ \Rightarrow |\overrightarrow a  \times \overrightarrow b | = |\overrightarrow c |\]

\[ \Rightarrow |\overrightarrow a ||\overrightarrow b |\sin \theta  = |\overrightarrow c |\]

\[ \Rightarrow |\overrightarrow a ||\overrightarrow b |\sin \frac{\pi }{2} = |\overrightarrow c |\] (Since vectors are mutually perpendicular, they are at a right angle with each other)

\[ \Rightarrow |\overrightarrow a ||\overrightarrow b | = |\overrightarrow c |\] (Since \[\sin \frac{\pi }{2} = 1\] ) ......(1)

Similarly, we have \[\overrightarrow b  \times \overrightarrow c  = \overrightarrow a \] .

\[ \Rightarrow |\overrightarrow b  \times \overrightarrow c | = |\overrightarrow a |\]

\[ \Rightarrow |\overrightarrow b ||\overrightarrow c |\sin \theta  = |\overrightarrow a |\]

\[ \Rightarrow |\overrightarrow b ||\overrightarrow c |\sin \frac{\pi }{2} = |\overrightarrow a |\] (Since vectors are mutually perpendicular, they are at a right angle with each other)

\[ \Rightarrow |\overrightarrow b ||\overrightarrow c | = |\overrightarrow a |\] (Since \[\sin \frac{\pi }{2} = 1\] ) ......(2)

Divide (2) by (1) :

\[ \Rightarrow \frac{{|\overrightarrow a ||\overrightarrow b |}}{{|\overrightarrow b ||\overrightarrow c |}} = \frac{{|\overrightarrow c |}}{{|\overrightarrow a |}}\]

\[ \Rightarrow \frac{{|\overrightarrow a |}}{{|\overrightarrow c |}} = \frac{{|\overrightarrow c |}}{{|\overrightarrow a |}}\]

\[ \Rightarrow |\overrightarrow a {|^2} = |\overrightarrow c {|^2}\]

\[ \Rightarrow |\overrightarrow a | = |\overrightarrow c |\] ......(3)

Substituting (3) in (2) :

\[|\overrightarrow b ||\overrightarrow a | = |\overrightarrow a |\]

\[ \Rightarrow |\overrightarrow b | = 1\]

Hence proved.

52. If \[\mathbf{\overrightarrow a  = 2\hat i - 3\hat j}\] , \[\mathbf{\overrightarrow b  = \hat i + \hat j - \hat k}\] and \[\mathbf{\overrightarrow c  = 3\hat i - \hat k}\] , find \[\mathbf{[\overrightarrow a \overrightarrow b \overrightarrow c ]}\] .

Ans: It is given that \[\overrightarrow a  = 2\hat i - 3\hat j\] , \[\overrightarrow b  = \hat i + \hat j - \hat k\] and \[\overrightarrow c  = 3\hat i - \hat k\] .

We know that \[[\overrightarrow a \overrightarrow b \overrightarrow c ] = \left( {\begin{array}{*{20}{c}} {{a_1}}&{{a_2}}&{{a_3}}\\ {{b_1}}&{{b_2}}&{{b_3}}\\ {{c_1}}&{{c_2}}&{{c_3}} \end{array}} \right)\]

\[ \Rightarrow [\overrightarrow a \overrightarrow b \overrightarrow c ] = \left( {\begin{array}{*{20}{c}} 2&{ - 3}&0\\ 1&1&{ - 1}\\ 3&0&{ - 1} \end{array}} \right)\]

\[ \Rightarrow [\overrightarrow a \overrightarrow b \overrightarrow c ] = 2( - 1) + 3( - 1 + 3) + 0\]

\[ \Rightarrow [\overrightarrow a \overrightarrow b \overrightarrow c ] =  - 2 + 6\]

\[ \Rightarrow [\overrightarrow a \overrightarrow b \overrightarrow c ] = 4\]

53. Find volume of parallelepiped whose coterminous edges are given by vectors \[\mathbf{\overrightarrow a  = 2\hat i + 3\hat j + 4\hat k}\] , \[\mathbf{\overrightarrow b  = \hat i + 2\hat j - \hat k}\] and \[\mathbf{\overrightarrow c  = 3\hat i - \hat j + 2\hat k}\] .

Ans: To find the volume of parallelepiped whose coterminous edges are given by vectors \[\overrightarrow a  = 2\hat i + 3\hat j + 4\hat k\] , \[\overrightarrow b  = \hat i + 2\hat j - \hat k\] and \[\overrightarrow c  = 3\hat i - \hat j + 2\hat k\] , we simply take the scalar triple product of them:

\[[\overrightarrow a \overrightarrow b \overrightarrow c ] = \left| {\begin{array}{*{20}{c}} {{a_1}}&{{a_2}}&{{a_3}}\\ {{b_1}}&{{b_2}}&{{b_3}}\\ {{c_1}}&{{c_2}}&{{c_3}} \end{array}} \right|\]

\[ \Rightarrow [\overrightarrow a \overrightarrow b \overrightarrow c ] = \left| {\begin{array}{*{20}{c}} 2&3&4\\ 1&2&{ - 1}\\ 3&{ - 1}&2 \end{array}} \right|\]

\[ \Rightarrow [\overrightarrow a \overrightarrow b \overrightarrow c ] = \left| {2(3) - 3(5) + 4( - 7)} \right|\]

\[ \Rightarrow [\overrightarrow a \overrightarrow b \overrightarrow c ] = \left| {6 - 15 - 28} \right|\]

\[ \Rightarrow [\overrightarrow a \overrightarrow b \overrightarrow c ] = \left| { - 37} \right|\]

Hence, the volume of parallelepiped is \[37\] cubic units.

54. Find the value of \[\lambda \] such that \[\mathbf{\overrightarrow a  = \hat i - \hat j + \hat k}\] , \[\mathbf{\overrightarrow b  = 2\hat i + \hat j - \hat k}\] and \[\mathbf{\overrightarrow c  = \lambda \hat i - \hat j + \lambda \hat k}\] are coplanar.

Ans: When three vectors are coplanar, their scalar triple product is zero.

We have \[\overrightarrow a  = \hat i - \hat j + \hat k\] , \[\overrightarrow b  = 2\hat i + \hat j - \hat k\] and \[\overrightarrow c  = \lambda \hat i - \hat j + \lambda \hat k\] .

\[[\overrightarrow a \overrightarrow b \overrightarrow c ] = \left| {\begin{array}{*{20}{c}} {{a_1}}&{{a_2}}&{{a_3}}\\ {{b_1}}&{{b_2}}&{{b_3}}\\ {{c_1}}&{{c_2}}&{{c_3}} \end{array}} \right|\]

\[ \Rightarrow \left| {\begin{array}{*{20}{c}} 1&{ - 1}&1\\ 2&1&{ - 1}\\ \lambda &{ - 1}&\lambda \end{array}} \right| = 0\]

\[ \Rightarrow \left| {(\lambda  - 1) + (2\lambda  + \lambda ) + ( - 2 - \lambda )} \right| = 0\]

\[ \Rightarrow \left| {(3\lambda  - 3)} \right| = 0\]

\[ \Rightarrow \lambda  = 1\]

55. Show that the four points \[\mathbf{\left( {--1,{\rm{ }}4,{\rm{ }}--3} \right)}\] , \[\mathbf{\left( {3,{\rm{ }}2,{\rm{ }}--5} \right)}\] , \[\mathbf{\left( {--3,{\rm{ }}8,{\rm{ }}--5} \right)}\] , \[\mathbf{\left( {--3,{\rm{ }}2,{\rm{ }}1} \right)}\] are coplanar.

Ans: Given the four points A \[\left( {--1,{\rm{ }}4,{\rm{ }}--3} \right)\] , B \[\left( {3,{\rm{ }}2,{\rm{ }}--5} \right)\] , C \[\left( {3,{\rm{ }}2,{\rm{ }}--5} \right)\] , D \[\left( {--3,{\rm{ }}2,{\rm{ }}1} \right)\] :

Now, \[\overrightarrow {AB}  = \overrightarrow b  - \overrightarrow a \]

\[ \Rightarrow \overrightarrow {AB}  = 4\hat i - 2\hat j - 2\hat k\]

\[\overrightarrow {AC}  = \overrightarrow c  - \overrightarrow a \]

\[ \Rightarrow \overrightarrow {AC}  =  - 2\hat i + 4\hat j - 2\hat k\]

\[\overrightarrow {AD}  = \overrightarrow d  - \overrightarrow a \]

\[ \Rightarrow \overrightarrow {AD}  =  - 2\hat i - 2\hat j + 4\hat k\]

For the points A, B, C and D to be coplanar, we need to show that vectors \[\overrightarrow {AB} ,\overrightarrow {AC} \overrightarrow {,AD} \] are coplanar, that is, their triple product should be equal to zero. 

\[[\overrightarrow {AB} \overrightarrow {AC} \overrightarrow {AD} ] = \left| {\begin{array}{*{20}{c}} {{a_1}}&{{a_2}}&{{a_3}}\\ {{b_1}}&{{b_2}}&{{b_3}}\\ {{c_1}}&{{c_2}}&{{c_3}} \end{array}} \right|\]

\[ \Rightarrow [\overrightarrow {AB} \overrightarrow {AC} \overrightarrow {AD} ] = \left| {\begin{array}{*{20}{c}} 4&{ - 2}&{ - 2}\\ { - 2}&4&{ - 2}\\ { - 2}&{ - 2}&4 \end{array}} \right|\]

\[ \Rightarrow [\overrightarrow {AB} \overrightarrow {AC} \overrightarrow {AD} ] = \left| {4(12) + 2( - 12) - 2(12)} \right|\]

\[ \Rightarrow [\overrightarrow {AB} \overrightarrow {AC} \overrightarrow {AD} ] = \left| {48 - 24 - 24} \right|\]

\[ \Rightarrow [\overrightarrow {AB} \overrightarrow {AC} \overrightarrow {AD} ] = 0\]

Hence proved.

56. For any three vectors \[\mathbf{\overrightarrow a ,\overrightarrow b ,\overrightarrow c} \] prove that \[\mathbf{[\overrightarrow a  + \overrightarrow b  \cdot \overrightarrow b  + \overrightarrow c  \cdot \overrightarrow c  + \overrightarrow a ] = 2[\overrightarrow a  \cdot \overrightarrow b  \cdot \overrightarrow c ]}\] .

Ans: Let us consider \[[\overrightarrow a  + \overrightarrow b  \cdot \overrightarrow b  + \overrightarrow c  \cdot \overrightarrow c  + \overrightarrow a ]\] :

\[ \Rightarrow (\overrightarrow a  + \overrightarrow b ) \cdot [(\overrightarrow b  + \overrightarrow c ) \times (\overrightarrow c  + \overrightarrow a )]\]

\[ \Rightarrow (\overrightarrow a  + \overrightarrow b ) \cdot (\overrightarrow b  \times \overrightarrow c  + \overrightarrow c  \times \overrightarrow c  + \overrightarrow b  \times \overrightarrow a  + \overrightarrow c  \times \overrightarrow a )\]

\[ \Rightarrow (\overrightarrow a  + \overrightarrow b ) \cdot (\overrightarrow b  \times \overrightarrow c  + \overrightarrow b  \times \overrightarrow a  + \overrightarrow c  \times \overrightarrow a )\] (Since \[\overrightarrow c  \times \overrightarrow c  = 0\] )

\[ \Rightarrow \overrightarrow a  \cdot (\overrightarrow b  \times \overrightarrow c ) + \overrightarrow b  \cdot (\overrightarrow b  \times \overrightarrow c ) + \overrightarrow a  \cdot (\overrightarrow b  \times \overrightarrow a ) + \overrightarrow b  \cdot (\overrightarrow b  \times \overrightarrow a ) + \overrightarrow a  \cdot (\overrightarrow c  \times \overrightarrow a ) + \overrightarrow b  \cdot (\overrightarrow c  \times \overrightarrow a )\]

\[ \Rightarrow \overrightarrow a  \cdot (\overrightarrow b  \times \overrightarrow c ) + \overrightarrow b  \cdot (\overrightarrow c  \times \overrightarrow a )\] (Since \[\overrightarrow b  \cdot (\overrightarrow b  \times \overrightarrow c ) = \overrightarrow a  \cdot (\overrightarrow b  \times \overrightarrow a ) = \overrightarrow b  \cdot (\overrightarrow b  \times \overrightarrow a ) = \overrightarrow a  \cdot (\overrightarrow c  \times \overrightarrow a ) = 0\] )

\[ \Rightarrow \overrightarrow a  \cdot (\overrightarrow b  \times \overrightarrow c ) + \overrightarrow a  \cdot (\overrightarrow b  \times \overrightarrow c )\] (Since \[\overrightarrow b  \cdot (\overrightarrow c  \times \overrightarrow a ) = \overrightarrow a  \cdot (\overrightarrow b  \times \overrightarrow c )\] )

\[ \Rightarrow 2[\overrightarrow a \overrightarrow b \overrightarrow c ]\]

Hence proved. 

57. For any three vectors \[\mathbf{\overrightarrow a ,\overrightarrow b ,\overrightarrow c }\] prove that \[\mathbf{\overrightarrow a  - \overrightarrow b ,\overrightarrow b  - \overrightarrow c ,\overrightarrow c  - \overrightarrow a }\] are coplanar.

Ans: For \[\overrightarrow a  - \overrightarrow b ,\overrightarrow b  - \overrightarrow c ,\overrightarrow c  - \overrightarrow a \] to be coplanar, their scalar product should be equal to zero.

\[ \Rightarrow [\overrightarrow a  - \overrightarrow b  \cdot \overrightarrow b  - \overrightarrow c  \cdot \overrightarrow c  - \overrightarrow a ]\]

\[ \Rightarrow (\overrightarrow a  - \overrightarrow b ) \cdot [(\overrightarrow b  - \overrightarrow c ) \times (\overrightarrow c  - \overrightarrow a )]\]

\[ \Rightarrow (\overrightarrow a  - \overrightarrow b ) \cdot (\overrightarrow b  \times \overrightarrow c  - \overrightarrow c  \times \overrightarrow c  - \overrightarrow b  \times \overrightarrow a  + \overrightarrow c  \times \overrightarrow a )\]

\[ \Rightarrow (\overrightarrow a  - \overrightarrow b ) \cdot (\overrightarrow b  \times \overrightarrow c  - \overrightarrow b  \times \overrightarrow a  + \overrightarrow c  \times \overrightarrow a )\] (Since \[\overrightarrow c  \times \overrightarrow c  = 0\] )

\[ \Rightarrow \overrightarrow a  \cdot (\overrightarrow b  \times \overrightarrow c ) - \overrightarrow b  \cdot (\overrightarrow b  \times \overrightarrow c ) - \overrightarrow a  \cdot (\overrightarrow b  \times \overrightarrow a ) + \overrightarrow b  \cdot (\overrightarrow b  \times \overrightarrow a ) + \overrightarrow a  \cdot (\overrightarrow c  \times \overrightarrow a ) - \overrightarrow b  \cdot (\overrightarrow c  \times \overrightarrow a )\]

\[ \Rightarrow \overrightarrow a  \cdot (\overrightarrow b  \times \overrightarrow c ) - \overrightarrow b  \cdot (\overrightarrow c  \times \overrightarrow a )\] (Since \[\overrightarrow b  \cdot (\overrightarrow b  \times \overrightarrow c ) = \overrightarrow a  \cdot (\overrightarrow b  \times \overrightarrow a ) = \overrightarrow b  \cdot (\overrightarrow b  \times \overrightarrow a ) = \overrightarrow a  \cdot (\overrightarrow c  \times \overrightarrow a ) = 0\] )

\[ \Rightarrow [\overrightarrow a \overrightarrow b \overrightarrow c ] - [\overrightarrow a \overrightarrow b \overrightarrow c ]\] (Since \[\overrightarrow b  \cdot (\overrightarrow c  \times \overrightarrow a ) = \overrightarrow a  \cdot (\overrightarrow b  \times \overrightarrow c )\] )

\[ \Rightarrow 0\]

Hence proved.

Related Study Materials for Class 12 Maths Chapter 10 Vector Algebra

CBSE Class 12 Maths Chapter-wise Important Questions

CBSE Class 12 Maths Chapter-wise Important Questions and Answers cover topics from all 13 chapters, helping students prepare thoroughly by focusing on key topics for easier revision.

Additional Study Materials for Class 12 Maths