
Maths Notes for Chapter 11 Three-Dimensional Geometry Class 12 - FREE PDF Download
In the Maths Chapter 11 Three-Dimensional Geometry Class 12 Notes, students will learn about the essentials of 3D geometry, including coordinate systems, distance formulas, and equations of planes and lines. Our notes provide clear explanations and important formulas to help you understand and excel in this topic.
Take advantage of the FREE PDF download to access these valuable resources anytime, anywhere. Visit our pages to get your Class 12 Maths Notes and check out the Class 12 Maths Syllabus to stay on track with your studies.



Access Revision Notes For Class 12 Maths Chapter 11 Three-Dimensional Geometry
1. Direction Cosines and Direction Ratios
(i) Consider a line OP passing through origin.

The angles the line OP makes with the $x,y$ and $z$ axes are $\alpha, \beta$ and $\gamma$. Then, $\cos \alpha, \cos \beta$ and $\cos \gamma$ are the direction cosines of the line OP. They are represented as:
$l=\cos \alpha, m = \cos \beta, n =\ cos \gamma$
(ii) For lines not passing through the origin, the direction cosines are found using the direction ratios.
Consider line AB. Now draw line parallel to line AB passing through origin, i.e., OP.
Two parallel lines have the same direction cosines.

So, $a,b,c$ will be proportional to the $l,m,n$ then $a,b,c$ are the Direction Ratios of the line, such that
$a=kl, b=km, c=kn$
(iii) If $a,b,c$ are the direction ratio of any line, then the vector parallel to this line will be \[a\hat{i}+b\hat{j}+c\hat{k}\].
(iv) If $l,m,n$ are direction cosines of any line, then the unit vector parallel to this line will be \[l\hat{i}+m\hat{j}+n\hat{k}\].
2. Relation between the direction cosines and direction ratios of a line
(i) If $l,m,n$ are direction cosines of a line, then
\[{{l}^{2}}+{{m}^{2}}+{{n}^{2}}=1\]
(ii) If $l,m,n$ are direction cosines and $a,b,c$ are direction ratios of a vector, then
$l=\pm \dfrac{a}{\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}},m=\pm \dfrac{b}{\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}},n=\pm \dfrac{c}{\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}}$
3. Direction cosines and Direction ratios of a line passing through two points
(i) Let two points be A and B such that their coordinates are $\left( {{x}_{1}},{{y}_{1}},{{z}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}},{{z}_{2}} \right)$ respectively. Then the direction cosines of a line passing through AB are:
\[l=\dfrac{{{x}_{2}}-{{x}_{1}}}{\left| AB \right|},m=\dfrac{{{y}_{2}}-{{y}_{1}}}{\left| AB \right|},n=\dfrac{{{z}_{2}}-{{z}_{1}}}{\left| AB \right|}\]
Where $AB=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}+{{\left( {{z}_{2}}-{{z}_{1}} \right)}^{2}}}$
And the direction ratios of the line AB are:
\[a={{x}_{2}}-{{x}_{1}},b={{y}_{2}}-{{y}_{1}},c={{z}_{2}}-{{z}_{1}}\]
4. Equation of a line in space
(i) Equation of line through a given point and parallel to a vector:
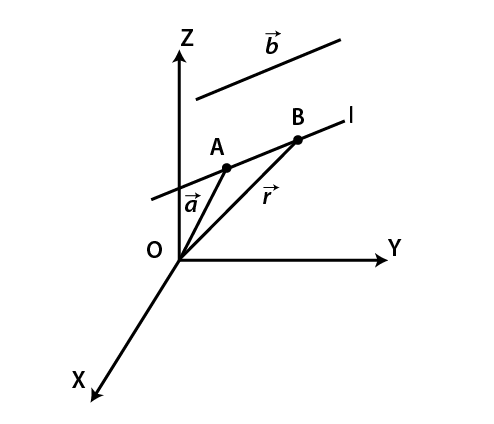
The vector equation of line passing through point A with position vector $\vec a$ and parallel to vector $\vec b$ is given by:
$\vec r=\vec a+\lambda\vec b$
The Cartesian equation of line passing through point A $(x_1,y_1,z_1)$ with direction ratios $a,b,c$ is given by:
\[\dfrac{x-{{x}_{1}}}{a},\dfrac{y-{{y}_{1}}}{b},\dfrac{z-{{z}_{1}}}{c}=r\]
The general point on this line will be given by: $\left( {{x}_{1}}+ar,{{y}_{1}}+br,{{z}_{1}}+cr \right)$
(ii) Equation of line through a two given points:
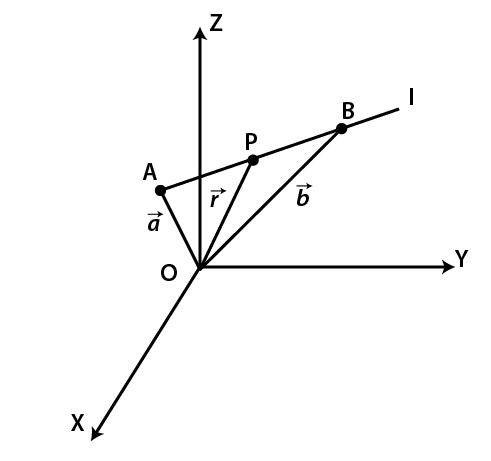
The vector equation of line passing through point A with position vector $\vec a$ and point B with position vector $\vec b$ is given by:
$\vec{r}=\vec{a}+\lambda \left( \vec{b}-\vec{a} \right)$
The Cartesian equation of line passing through point A $(x_1,y_1,z_1)$ and B $({{x}_{2}},{{y}_{2}},{{z}_{2}})$ is given by:
\[\dfrac{x-{{x}_{1}}}{{{x}_{2}}-{{x}_{1}}}=\dfrac{y-{{y}_{1}}}{{{y}_{2}}-{{y}_{1}}}=\dfrac{z-{{z}_{1}}}{{{z}_{2}}-{{z}_{1}}}\]
The general point on this line will be given by: $\left( {{x}_{1}}+ar,{{y}_{1}}+br,{{z}_{1}}+cr \right)$
5. Angle between two line segments
(i) The angle between two lines with direction ratios ${{a}_{1}},{{b}_{1}},{{c}_{1}}$ and ${{a}_{2}},{{b}_{2}},{{c}_{2}}$ is given by:
\[\cos \theta =\dfrac{{{a}_{1}}{{a}_{2}}+{{b}_{1}}{{b}_{2}}+{{c}_{1}}{{c}_{2}}}{\sqrt{a_{1}^{2}+b_{1}^{2}+c_{1}^{2}}\sqrt{a_{2}^{2}+b_{2}^{2}+c_{2}^{2}}}\]
Here \[{{a}_{1}}\hat{i}+{{b}_{1}}\hat{j}+{{c}_{1}}\hat{k}\] and \[{{a}_{2}}\hat{i}+{{b}_{2}}\hat{j}+{{c}_{2}}\hat{k}\] are two vector parallel to the given two lines respectively.
(ii) The two lines are perpendicular if \[{{a}_{1}}{{a}_{2}}+{{b}_{1}}{{b}_{2}}+{{c}_{1}}{{c}_{2}}=0\].
(iii) The two lines are parallel if \[\dfrac{{{a}_{1}}}{{{a}_{2}}}=\dfrac{{{b}_{1}}}{{{b}_{2}}}=\dfrac{{{c}_{1}}}{{{c}_{2}}}\].
6. Skew Lines
(i) The lines which are not parallel nor lying in the same plane, i.e., they are not intersecting are known as Skew Lines. The condition for skew lines is:
\[\Delta =\left| \begin{matrix} \alpha '-\alpha & \beta '-\beta & \gamma '-\gamma \\ l & m & n \\ l' & m' & n' \\ \end{matrix} \right|\ne 0\]
(ii) The vector condition for two lines to be skew are:
$\left( {{{\vec{b}}}_{1}}\times {{{\vec{b}}}_{2}} \right).\left( {{{\vec{a}}}_{1}}\times {{{\vec{a}}}_{2}} \right)\ne 0$
7. Shortest Distance between Two Lines
(i) Distance between two skew lines, $l_1$ and $l_2$ with equations $\vec r=\vec a_1+\lambda \vec b_1$ and $\vec r=\vec a_2+\mu \vec b_2$ is given by:
\[d=\left| \dfrac{\left( {{{\vec{b}}}_{1}}\times {{{\vec{b}}}_{2}} \right).\left( {{{\vec{a}}}_{2}}\times {{{\vec{a}}}_{1}} \right)}{\left( \left| {{{\vec{b}}}_{1}}\times {{{\vec{b}}}_{2}} \right| \right)} \right|\]
(ii) The Cartesian distance between two skew lines, $l_1$ and $l_2$ is given by:
\[d=\left | \frac{\begin{vmatrix}x_2-x_1 &y_2-y_1 & z_2-z_1\\ a_1 &b_1 & c_1\\ a_2 & b_2 & c_2 \end{vmatrix}}{\sqrt{(b_1c_2-b_2c_1)^2+(c_1a_2-c_2a_1)^2+(a_1b_2-a_2b_1)^2}} \right |\]
Where \[{{l}_{1}}=\dfrac{x-{{x}_{1}}}{{{a}_{1}}}=\dfrac{y-{{y}_{1}}}{{{b}_{1}}}=\dfrac{z-{{z}_{1}}}{{{c}_{1}}},{{l}_{2}}=\dfrac{x-{{x}_{2}}}{{{a}_{2}}}=\dfrac{y-{{y}_{2}}}{{{b}_{2}}}=\dfrac{z-{{z}_{2}}}{{{c}_{2}}}\] are the skew lines.
(iii) Distance between two parallel lines, $l_1$ and $l_2$ with equations $\vec r=\vec a_1+\lambda \vec b_1$ and $\vec r=\vec a_2+\mu \vec b_2$ is given by:
\[d=\left| \dfrac{\vec{b}\times \left( {{{\vec{a}}}_{2}}-{{{\vec{a}}}_{1}} \right)}{\left| {\vec{b}} \right|} \right|\]
8. Equation of a plane
(i) Vector form of equation of plane in normal form is given by:
$\vec{r}.\hat{n}=d$
Where $\vec r$ is the position vector of the point on the given plane, $\hat{n}$ is the normal unit vector to the plane from the origin and $d$ is the length of the normal unit vector from the origin to the plane.
(ii) Cartesian form of equation of plane in normal form is given by:
$lx+my+nz=d$
Where $P(x,y,z)$ is any point on the given plane, $\hat{n}$ is the normal unit vector to the plane from the origin and $l,m,n$ are the direction cosines of the normal unit vector.
(iii) If $\vec{r}.\left( a\hat{i}+b\hat{j}+c\hat{k} \right)=d$ is the vector equation of the plane, then the Cartesian equation of the plane will be $\left( ax+by+cz \right)=d$. Here $a,b,c$ are the direction ratios of the normal to the plane.
9. Equation of a plane perpendicular to a given vector and passing through a given point
(i) The vector form of the equation of the plane is:
$\left( \vec{r}-\vec{a} \right).\vec{N}=0$
Where $\vec r$ is the position vector of the any point on the given plane, $\vec{N}$ is the given vector to the plane from origin and $\vec{a}$ is the position vector of the given point on the given plane
(ii) Cartesian form of equation of plane is given by:
$A\left( x-{{x}_{1}} \right)+B\left( y-{{y}_{1}} \right)+C\left( z-{{z}_{1}} \right)=0$
Where $P(x,y,z)$ is the any point on the given plane, $({{x}_{1}},{{y}_{1}},{{z}_{1}})$ is the given point on the given plane and $A,B,C$ are the direction ratios of the given vector.
10. Equation of a plane passing through three non collinear points
(i) The vector form of the equation of the plane is:
$\left( \vec{r}-\vec{a} \right).\left[ \left( \vec{b}-\vec{a} \right)\times \left( \vec{c}-\vec{a} \right) \right]=0$
Where $\vec r$ is the position vector of the any point on the given plane, $\vec{a},\vec{b},\vec{c}$ are the position vectors of the three non collinear points on the plane.
(ii) Cartesian form of equation of plane is given by:
\[\left| \begin{matrix} x-{{x}_{1}} & y-{{y}_{1}} & z-{{z}_{1}} \\ {{x}_{2}}-{{x}_{1}} & {{y}_{2}}-{{y}_{1}} & {{z}_{2}}-{{z}_{1}} \\ {{x}_{3}}-{{x}_{1}} & {{y}_{3}}-{{y}_{1}} & {{z}_{3}}-{{z}_{1}} \\ \end{matrix} \right|=0\]
Where $P(x,y,z)$ is the any point on the given plane, $({{x}_{1}},{{y}_{1}},{{z}_{1}}),({{x}_{2}},{{y}_{2}},{{z}_{2}}),({{x}_{3}},{{y}_{3}},{{z}_{3}})$ are the three non collinear points on the plane.
11. Intercept form of the equation of a plane
(i) The equation is:
$\dfrac{x}{a}+\dfrac{y}{b}+\dfrac{z}{c}=1$
Where $a,b,c$ are the intercepts the plane makes with $x,y,z$ axes, respectively.
(ii) The plane intercepts the $x$ axis at $\left( a,0,0 \right)$. Similarly, the plane intercepts the $y$ axis at $\left( 0,b,0 \right)$ and the plane intersects the $z$ axis at $\left( 0,0,c \right)$.
12. Plane passing through the intersection of two given planes
(i) The vector form of equation of the plane passing through the intersection of the two given planes $\vec{r}.{{\hat{n}}_{1}}={{d}_{1}}$ and $\vec{r}.{{\hat{n}}_{2}}={{d}_{2}}$ is given by:
$\vec{r}.\left( {{{\vec{n}}}_{1}}+\lambda {{{\vec{n}}}_{2}} \right)={{d}_{1}}+\lambda {{d}_{2}}$
(ii) The Cartesian form of equation of the plane passing through the intersection of the two given planes ${{\vec{n}}_{1}}={{A}_{1}}\hat{i}+{{B}_{1}}\hat{j}+{{C}_{1}}\hat{k}$ and ${{\vec{n}}_{2}}={{A}_{2}}\hat{i}+{{B}_{2}}\hat{j}+{{C}_{2}}\hat{k}$ is given by:
$\left( {{A}_{1}}x+{{B}_{1}}y+{{C}_{1}}z-{{d}_{1}} \right)+\lambda \left( {{A}_{2}}x+{{B}_{2}}y+{{C}_{2}}z-{{d}_{2}} \right)=0$
13. Coplanar lines
(i) Two lines are coplanar if:
\[\left| \begin{matrix} \alpha -\alpha ' & \beta -\beta ' & \gamma -\gamma ' \\ l & m & n \\ l' & m' & n' \\ \end{matrix} \right|=0\]
Where \[\dfrac{x-\alpha }{l}=\dfrac{y-\beta }{m}=\dfrac{z-\gamma }{n}\] and \[\dfrac{x-\alpha '}{l'}=\dfrac{y-\beta '}{m'}=\dfrac{z-\gamma '}{n'}\] are the two lines.
(ii) The plane containing the coplanar lines is:
\[\left| \begin{matrix} x-\alpha & y-\beta & z-\gamma \\ l & m & n \\ l' & m' & n' \\ \end{matrix} \right|=0\]
(iii) The condition for coplanarity in vector form:
$\left( {{{\vec{a}}}_{2}}-{{{\vec{a}}}_{1}} \right).\left( {{{\vec{b}}}_{1}}\times {{{\vec{b}}}_{2}} \right)=0$
Where $\vec{r}={{\vec{a}}_{1}}+\lambda {{\vec{b}}_{1}}$ and $\vec{r}={{\vec{a}}_{2}}+\lambda {{\vec{b}}_{2}}$ are the given lines.
14. Angle between two planes
(i) Angle between the two normal to the two planes is known as the angle between the two planes.
(ii) The vector form of the angle between the two planes is given by:
$\cos \theta =\left| \dfrac{{{{\vec{n}}}_{1}}.{{{\vec{n}}}_{2}}}{\left| {{{\vec{n}}}_{1}} \right|\left| {{{\vec{n}}}_{2}} \right|} \right|$
Where ${{\vec{n}}_{1}},{{\vec{n}}_{2}}$ are the two normal to the two planes respectively.
(iii) The Cartesian form of the angle between the two planes is given by:
\[\cos \theta =\left| \dfrac{{{A}_{1}}{{A}_{2}}+{{B}_{1}}{{B}_{2}}+{{C}_{1}}{{C}_{2}}}{\sqrt{A_{1}^{2}+B_{1}^{2}+C_{1}^{2}}\sqrt{A_{2}^{2}+B_{2}^{2}+C_{2}^{2}}} \right|\]
Where ${{A}_{1}},{{B}_{1}},{{C}_{1}}$ and ${{A}_{2}},{{B}_{2}},{{C}_{2}}$ are the direction ratios of the normal to the given planes.
(iv) The planes are perpendicular to each other if ${{\vec{n}}_{1}}.{{\vec{n}}_{2}}=0$ or \[{{A}_{1}}{{A}_{2}}+{{B}_{1}}{{B}_{2}}+{{C}_{1}}{{C}_{2}}=0\].
(v) The planes are parallel to each other if ${{\vec{n}}_{1}}$ is parallel to ${{\vec{n}}_{2}}$ or $\dfrac{{{A}_{1}}}{{{A}_{2}}}=\dfrac{{{B}_{1}}}{{{B}_{2}}}=\dfrac{{{C}_{1}}}{{{C}_{2}}}$.
15. Distance of a Point from a Plane
(i) The vector form of the distance is:
$\left| d-\vec{a}.\hat{n} \right|$
Where $\vec{a}$ is the position vector of the given point and $\vec{r}.\hat{n}=d$ is the equation of the plane.
(ii) The Cartesian form of the distance is:
\[\left| \dfrac{A{{x}_{1}}+B{{y}_{1}}+C{{z}_{1}}-D}{\sqrt{{{A}^{2}}+{{B}^{2}}+{{C}^{2}}}} \right|\]
Where $P({{x}_{1}},{{y}_{1}},{{z}_{1}})$ is the given point and $Ax+By+Cz=D$ is the Cartesian equation of the plane.
(iii) When $\vec{r}.\vec{N}=d$ is the equation of the plane and $\vec{N}$ normal to the plane, then the perpendicular distance is given by:
$\dfrac{\left| \vec{a}.\vec{N}-d \right|}{\left| {\vec{N}} \right|}$
(iv) The perpendicular distance from origin to the plane $\vec{r}.\vec{N}=d$ is given by:
$\dfrac{\left| d \right|}{\left| {\vec{N}} \right|}$
16. Angle between a line and a plane
(i) The complement of the angle between the normal to the plane and the line is known as the angle between the line and the plane.
(ii) The vector form of the angle between the line and the plane is given by:
$\sin \left( 90-\theta \right)=\cos \theta =\left| \dfrac{\vec{b}.\vec{n}}{\left| {\vec{b}} \right|\left| {\vec{n}} \right|} \right|$
Where $\vec{r}=\vec{a}+\lambda \vec{b}$ is the equation of the line and $\vec{r}.\vec{n}=d$ is the equation the plane.
Three Dimensional Geometry Class 12 Notes Maths - Basic Subjective Questions
Section–A (1 Mark Questions)
1. Find the distance of the plane $\vec{r}.\left ( \frac{2}{7}\hat{i}+\frac{3}{7}\hat{j}-\frac{6}{7}\hat{k} \right )=1$ from the origin.
Ans. The general equation of a plane in vector from is given by $\vec{r}, \hat{n}=d$ where $d$ is the distance of the plane from the origin. Comparing
$\vec{r} \cdot \hat{n}=d$ and $\vec{r} \cdot\left(\frac{2}{7} \hat{i}+\frac{3}{7} \hat{j}-\frac{6}{7} \hat{k}\right)=1$, we get $d=1$.
2. If the plane 2x-3y+6z-11=0 makes an angle $sin^{-1}\alpha$ with x-axis, then find the value of $\alpha$ .
Ans. We are given that, $2 x-3 y+6 z-11=0$ makes an angle $\sin ^{-1} \alpha$ with $x$-axis The equation
of plane $2 x-3 y+6 z-11=0$ in vector form is given by $\vec{r} \cdot(2 \hat{i}-3 \hat{j}+6 \hat{k})=11$
$\therefore \vec{b}=(\hat{i}+0 \hat{j}+0 \hat{k})$ and $\vec{n}=2 \hat{i}-3 \hat{j}+6 \hat{k}$
We know that,
$\sin \theta=\frac{\left | \vec{b}\;\vec{n} \right |}{\left | \vec{b} \right |\left | \vec{n} \right |}$
$\sin \theta=\frac{|(\hat{i}) \cdot(2 \hat{i}-3 \hat{j}+6 \hat{k})|}{\sqrt{1}\sqrt{4+9+36}}=\frac{2}{7}$
3. If a plane passes through the points (2,0,0),(0,3,0) and (0,0,4) and then find the equation of plane.
Ans. The equation of the plane that cut the coordinate axes at $(a, 0,0)(0, b, 0)$ and $(0,0, c)$ is given by $\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1$.
Hence, the equation of plane passing through the points $(2,0,0),(0,3,0)$ and $(0,0,4)$ is $\frac{x}{2}+\frac{y}{3}+\frac{z}{4}=1$
$\Rightarrow 6 x+4 y+3 z=12$
4. Find the vector equation of the line through the points (3,4,-7) and (1,-1,6).
Ans. The vector equation of a line passing through two points is given by
$$\vec{r}=\vec{a}+\lambda(\vec{b}-\vec{a})$$
Here, $\vec{a}=3 \hat{i}+4 \hat{j}-7 \hat{k}$ and $\vec{b}=\hat{i}-\hat{j}+6 \hat{k}$
$$\therefore(\vec{b}-\vec{a})=-2 i-5 \hat{j}+13 \hat{k}$$
So, the required equation is
$$\vec{r}=3 \hat{i}+4 \hat{j}-7 \hat{k}+\lambda(-2 \hat{i}-5 \hat{j}+13 \hat{k})$$
5. Find the cartesian equation of the plane $\vec{r}.(\hat{i}+\hat{j}-\hat{k})=2$ .
Ans. We know that $\vec{r}=x \hat{i}+y \hat{j}+z \hat{k}$ Substituting
$\vec{r}=x \hat{i}+y \hat{j}+z \hat{k}$ in $\vec{r} \cdot(\hat{i}+\hat{j}-\hat{k})=2$,
we get $(x \hat{i}+y \hat{j}+z \hat{k}) \cdot(\hat{i}+\hat{j}-\hat{k})=2$
$\Rightarrow x+y-z=2$
Section–B (2 Marks Questions)
6. If the direction cosines of a line are k, k, and k, then find the value of k.
Ans. We know that, if $l, m, n$ are the direction cosines of a line, then $l^2+m^2+n^2=1$
Here, $l=k, m=k$ and $n=k$
Substituting $l=k, m=k$ and $n=k$ in
$$\begin{aligned}& l^2+m^2+n^2=1, \text { we get, } \\& \Rightarrow k^2+k^2+k^2=1 \\& \Rightarrow 3 k^2=1 \\& \Rightarrow k^2=\frac{1}{3} \\& \Rightarrow k= \pm \frac{1}{\sqrt{3}}\end{aligned}$$
7. Find the sine of the angle between the straight line $\frac{x-2}{3}=\frac{y-3}{4}=\frac{z-4}{5}$ and the plane 2x-2y+z=5.
Ans. We can write the equation of the line and plane in vector form as
$$\begin{aligned}& \dot{r}=2 \hat{i}+3 \hat{j}+4 \hat{k}+\lambda(3 \hat{i}+4 \hat{j}+5\hat{k}) \text { and } \\& \vec{r} \cdot(2 \hat{i}-2 \hat{j}+\hat{k})=5 \\& \therefore \vec{b}=3 \hat{i}+4 \hat{j}+5 \hat{k} \text { and } \vec{n}=2 \hat{i}-2\hat{j}+\hat{k}\end{aligned}$$
The angle between the line and the plane is
$$\sin \theta=\frac{|\vec{b} \vec{n}|}{|\vec{b}||\vec{n}|}$$
given bySubstituting
$\vec{b}=3 \hat{i}+4 \hat{j}+5 \hat{k}$ and $\vec{n}=2 \hat{i}-2 \hat{j}+\hat{k}$ in
$\sin \theta=\frac{|\vec{b} \cdot \vec{n}|}{|\vec{b}||\vec{n}|}$, we get
$$\begin{aligned}& \sin \theta=\frac{|(3 \hat{i}+4 \hat{j}+5 \hat{k}) \cdot(2 \hat{i}-2\hat{j}+\hat{k})|}{\sqrt{3^2+4^2+5^2} \cdot \sqrt{4+4+1}} \\ & =\frac{|6-8+5|}{\sqrt{50} \cdot 3} \\& =\frac{3}{15 \sqrt{2}} \\& =\frac{1}{5 \sqrt{2}}\end{aligned}$$
8. Find the unit vector normal to the plane x+2y+3z-6=0.
Ans. The unit vector normal to the plane $a x+b y+c z+d=0$ is given by
$\vec{n}=\frac{a \hat{i}}{\sqrt{a^2+b^2+c^2}}+\frac{b \hat{j}}{\sqrt{a^2+b^2+c^2}}+$
$\frac{c \hat{k}}{\sqrt{a^2+b^2+c^2}}$
Comparing $x+2 y+3 z-6=0$ with
$a x+b y+c z+d=0$, we get
$a=1, b=2$ and $c=3$
Substituting $a=1, b=2$ and $c=3$ in
$$\begin{aligned}& \bar{n}=\frac{a \hat{i}}{\sqrt{a^2+b^2+c^2}}+\frac{b \hat{j}}{\sqrt{a^2+b^2+c^2}} \\& +\frac{c \hat{k}}{\sqrt{a^2+b^2+c^2}},\end{aligned}$$
we get
$$\begin{aligned}& \vec{n}=\frac{\hat{i}}{\sqrt{1^2+2^2+3^2}}+\frac{2 \hat{j}}{\sqrt{1^2+2^2+3^2}} \\ & +\frac{3 \hat{k}}{\sqrt{1^2+2^2+3^2}} \\ & \Rightarrow \vec{n}=\frac{\hat{i}}{\sqrt{14}}+\frac{2 \hat{j}}{\sqrt{14}}+\frac{3 \hat{k}}{\sqrt{14}} \end{aligned} $$
9. Find the intercepts made by the plane 2x-3y-5z=0 on the coordinate axis.
Ans. We have, $2 x-3 y+5 z+4=0$
$$\begin{aligned}& \Rightarrow 2 x-3 y+5 z=-4 \\& \Rightarrow \frac{2 x}{-4}+\frac{3 y}{4}+\frac{5 z}{-4}=1\end{aligned}$$
$$\begin{aligned}&\Rightarrow\frac{x}{-\frac{4}{2}}+\frac{y}{\frac{4}{3}}+\frac{z}{-\frac{4}{5}}=1 \\& \Rightarrow \frac{x}{-2}+\frac{y}{\frac{4}{3}}+\frac{z}{\left(-\frac{4}{5}\right)}=1\end{aligned}$$
We know that, the intercepts made by the plane $\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1$ on the coordinate axis are $a, b$ and $c$.
Therefore, the intercepts made by the plane $2 x-3 y+5 z+4=0$ on the coordinate axis are $-2, \frac{4}{3}$ and $-\frac{4}{5}$.
10. Find the angle between the line $\vec{r}.(5\hat{i}-\hat{j}-4\hat{k})+\lambda (2\hat{i}-\hat{j}+\hat{k})$ and the plane $\vec{r}.(3\hat{i}-4\hat{j}-\hat{k})+ 5=0$.
Ans. We have,
$\vec{b}=2 \hat{i}-\hat{j}+\hat{k}$ and $r=3 \hat{i}-4 \hat{j}-\hat{k}$
Let $\theta$ be the angle between line and plane.
$$ \begin{aligned} & \therefore \sin \theta=\frac{|\vec{b}, \hat{n}|}{\left|\vec{b}^*\right||r|} \\ & \Rightarrow \sin \theta=\frac{|(2 \hat{i}-\hat{j}+\hat{k}) \cdot(3 \hat{i}-4 \hat{j}-\hat{k})|}{\sqrt{6} \cdot \sqrt{26}} \\ & \Rightarrow \sin \theta=\frac{|6+4-1|}{\sqrt{156}} \\ & \Rightarrow \sin \theta=\frac{9}{2 \sqrt{39}} \\ & \Rightarrow \theta=\sin ^{-1} \frac{9}{2 \sqrt{39}} \end{aligned} $$
11. Find the angle between the planes $\vec{r}.(2\hat{i}-3\hat{j}+\hat{k})=1$ and \vec{r}.(\hat{i}-\hat{j}) .
Ans. The angle between two planes
$\vec{r} \cdot \vec{n}_1=d_1$ and $\vec{r} \cdot \vec{n}_2=d_2$ is given by
$\cos \theta=\frac{\left|\vec{n}_1 \cdot \vec{n}_2\right|}{\left|\vec{n}_1\right|\left|\vec{n}_2\right|}$
Comparing
$$\vec{r} \cdot(2 \hat{i}-3 \hat{j}+\hat{k})=1 \text { and } \vec{r} \cdot(\hat{i}-\hat{j})=4 \text { with }$$
$\vec{r} \cdot \vec{n}_1=d_1$ and $\vec{r} \cdot \vec{n}_2=d_2$, we get
$$\vec{n}_1=(2 \hat{i}-3 \hat{j}+\hat{k}) \text { and } \vec{n}_2=(\hat{i}-\hat{j})$$
Substituting
$$ \begin{aligned} & \vec{n}_1=(2 \hat{i}-3 \hat{j}+\hat{k}) \text { and } \vec{n}_2=(\hat{i}-\hat{j})_{\text {in }} \\ & \cos \theta=\frac{\left|\vec{n}_1 \cdot \vec{n}_2\right|}{\left|\vec{n}_1\right|\left|\vec{n}_2\right| \text { we get }} \\ & \cos \theta=\frac{|(2 \hat{i}-3 \hat{j}+\hat{k}) \cdot(\hat{i}-\hat{j})|}{\sqrt{4+9+1} \sqrt{1+1}} \\ & \Rightarrow \cos \theta=\frac{|2+3|}{\sqrt{14} \cdot \sqrt{2}} \\ & \Rightarrow \cos \theta=\frac{5}{2 \sqrt{7}} \\ & \Rightarrow \theta=\cos ^{-1}\left(\frac{5}{2 \sqrt{7}}\right) \end{aligned} $$
12. Find the equation of a line, which is parallel to $(2\hat{i}+\hat{j}+3\hat{k})$ and which passes through the point (5,-2,4).
Ans. The equation of line parallel to $a \hat{i}+b \hat{j}+c \hat{k}$ and passing through the point $\left(x_1, y_1, z_1\right)$ is given by
$$\frac{x-x_1}{a}=\frac{y-y_1}{b}=\frac{z-z_1}{c}$$
Comparing $a \hat{i}+b \hat{j}+c \hat{k}$ and $2 \hat{i}+\hat{j}+3 \hat{k}$, we get
$a=2, b=1$ and $c=3$
We are also given the required line is passing through $(5,-2,4)$
$$\therefore x_1=5, y_1=-2, z_1=4$$
Thus, the required equation of line is
$$\frac{x-5}{2}=\frac{y+2}{1}=\frac{z-4}{3} \text {. }$$
13. If the foot of perpendicular drawn from the origin to a plane is (5,-3,-2), then find the equation of plane.
Ans. We are given that, the required plane passes through the point $P(5,-3,-2)$ and is perpendicular to $\overrightarrow{O P}$
$\therefore \vec{a}=5 \hat{i}-3 \hat{j}-2 \hat{k}$ and $\vec{n}=\overrightarrow{O P}=5 \hat{i}-3 \hat{j}-2 \hat{k}$
Now, the equation of the plane is
$$\begin{aligned}& (\vec{r}-\vec{a}) \cdot \vec{n}=0 \\& \Rightarrow \vec{r} \cdot\vec{n}=\vec{a} \cdot \vec{n}\end{aligned}$$
$\Rightarrow \vec{r}.(5\hat{i}-3\hat{j}-2\hat{k})= (5\hat{i}-3\hat{j}-2\hat{k}).\vec{r}.(5\hat{i}-3\hat{j}-2\hat{k})$
$\Rightarrow \vec{r}.(5\hat{i}-3\hat{j}-2\hat{k})=25+9+4$
$\Rightarrow \vec{r}.(5\hat{i}-3\hat{j}-2\hat{k})=38$
Important Formulas of Class 12 Maths Chapter 11 Three-Dimensional Geometry You Shouldn’t Miss!
1. Distance Formula Between Two Points:
For points \( A(x_1, y_1, z_1) \) and \( B(x_2, y_2, z_2) \):
\[AB = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2}\]
2. Midpoint Formula:
For points \( A(x_1, y_1, z_1) \) and \( B(x_2, y_2, z_2) \):
\[M = \left( \frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}, \frac{z_1 + z_2}{2} \right)\]
3. Equation of a Plane:
For a plane with normal vector \(\mathbf{n} = (a, b, c)\) passing through a point \((x_1, y_1, z_1)\):
\[a(x - x_1) + b(y - y_1) + c(z - z_1) = 0\]
Or in the general form:
\[ax + by + cz + d = 0\]
4. Distance of a Point from a Plane:
For a point \(P(x_1, y_1, z_1)\) and a plane \(ax + by + cz + d = 0\):
\[\text{Distance} = \frac{|ax_1 + by_1 + cz_1 + d|}{\sqrt{a^2 + b^2 + c^2}}\]
5. Direction Ratios of a Line:
For a line passing through points \( (x_1, y_1, z_1) \) and \( (x_2, y_2, z_2) \):
\[\text{Direction Ratios} = (x_2 - x_1, y_2 - y_1, z_2 - z_1)\]
6. Vector Equation of a Line:
For a line passing through point \( \mathbf{r}_0 \) with direction vector \( \mathbf{d} \):
\[\mathbf{r} = \mathbf{r}_0 + \lambda \mathbf{d}\]
7. Cartesian Equation of a Line:
For a line passing through \( (x_1, y_1, z_1) \) with direction ratios \( (a, b, c) \):
\[\frac{x - x_1}{a} = \frac{y - y_1}{b} = \frac{z - z_1}{c}\]
8. Angle Between Two Lines:
For lines with direction vectors \( \mathbf{a} \) and \( \mathbf{b} \):
\[\cos \theta = \frac{\mathbf{a} \cdot \mathbf{b}}{|\mathbf{a}| |\mathbf{b}|}\]
9. Angle Between Two Planes:
For planes with normal vectors \( \mathbf{n}_1 = (a_1, b_1, c_1) \) and \( \mathbf{n}_2 = (a_2, b_2, c_2) \):
\[\cos \theta = \frac{\mathbf{n}_1 \cdot \mathbf{n}_2}{|\mathbf{n}_1| |\mathbf{n}_2|}\]
10. Intersection of Two Planes:
For planes \( a_1x + b_1y + c_1z + d_1 = 0 \) and \( a_2x + b_2y + c_2z + d_2 = 0 \):
The line of intersection can be found by solving these equations simultaneously.
11. Shortest Distance Between Two Skew Lines:
For skew lines with direction vectors \( \mathbf{d}_1 \) and \( \mathbf{d}_2 \), and a vector \( \mathbf{d} \) connecting points on the two lines:
\[\text{Distance} = \frac{|\mathbf{d} \cdot (\mathbf{d}_1 \times \mathbf{d}_2)|}{|\mathbf{d}_1 \times \mathbf{d}_2|}\]
12. Equation of a Sphere:
For a sphere with center \( (h, k, l) \) and radius \( r \):
\[(x - h)^2 + (y - k)^2 + (z - l)^2 = r^2\]
Importance of Revision Notes
Foundational Knowledge: Class 12 Maths Chapter 11 Three-Dimensional Geometry Notes PDF introduces essential concepts like types of Three-Dimensional Geometry, and graphs of some particular functions which are fundamental for further study in mathematics.
Convenient Learning: The Three-Dimensional Geometry Class 12 Maths Notes PDF download offers easy access to comprehensive notes, allowing for flexible and on-the-go study.
Effective Revision: With clear explanations and examples, the notes support efficient revision and a deeper understanding of key concepts.
Enhanced Exam Preparation: The notes help consolidate knowledge, improving readiness for exams and boosting overall academic performance.
Accessible Resource: The Class 12 Maths Chapter 11 Three-Dimensional Geometry Notes PDF ensures that all students can benefit from quality study material without any cost.
Tips for Learning the Class 12 Maths Chapter 11 Three-Dimensional Geometry
Here are some effective tips for learning Class 12 Maths Chapter 11: Three-Dimensional
Geometry:
Understand Basic Concepts:
Begin with a clear understanding of the basic concepts such as coordinates in 3D space, distance between points, and equations of planes and lines.
Visualise in 3D:
Use diagrams and sketches to visualise points, lines, and planes in three-dimensional space. This helps in better understanding and solving geometric problems.
Master Key Formulas:
Memorise and practice using key formulas like distance between two points, midpoint formula, and equations of planes. Regular practice will help in retaining these formulas.
Practice with Examples:
Work through a variety of problems and examples to apply the concepts and formulas. This will help you understand how to approach different types of questions.
Understand Planes and Lines:
Focus on understanding the equations of planes and lines, and how to find their intersections and distances. These concepts are crucial for solving many problems in 3D geometry.
Solve Previous Year Papers:
Practice solving previous year's exam papers and sample questions. This will help you become familiar with the types of questions that may appear in exams.
Use Online Resources:
Utilise online resources such as educational videos, tutorials, and interactive tools to reinforce your understanding of three-dimensional geometry.
Conclusion
Mastering Class 12 Maths Chapter 11: Three-Dimensional Geometry is essential for understanding spatial relationships and solving complex geometric problems. By focusing on key concepts, practising essential formulas, and applying the methods to various problems, you can strengthen your grasp of 3D geometry. Regular review and practical application will enhance your problem-solving skills and prepare you effectively for exams. Utilise the provided notes and practice materials to excel in this chapter and build a solid foundation for advanced mathematics topics.
Related Study Materials for Class 12 Maths Chapter 11 Three-Dimensional Geometry
S.No | Three Dimensional Geometry Related Study Materials |
1. | CBSE Class 12 Maths Three Dimensional Geometry NCERT Solutions |
2. | CBSE Class 12 Maths Three Dimensional Geometry Important Questions |
3. | |
4. | CBSE Class 12 Maths Three Dimensional Geometry NCERT Exemplar |
Chapter-wise Revision Notes Links for Class 12 Maths
S.No | Revision Notes Links for Class 12 Maths |
1. | |
2. | |
3. | |
4. | |
5. | |
6. | |
7. | |
8. | |
9. | |
10. | |
11. | |
12. |
Important Study Materials for Class 12 Maths
S.No | Study Material for Class 12 Maths |
1. | |
2. | |
3. | |
4. | |
5. | |
6. | |
7. | |
8. | |
9. |






































