
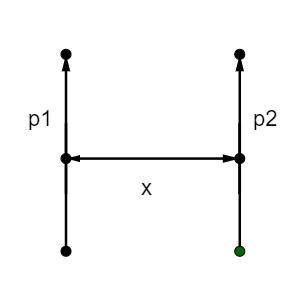
The force of interaction of two dipoles, if the two dipoles are parallel to each other and placed at distance x apart.
1. \[\dfrac{{3{p_1}{p_2}}}{{4\pi {\varepsilon _ \circ }{x^4}}}\]
2. \[\dfrac{{{p_1}{p_2}}}{{4\pi {\varepsilon _ \circ }{x^4}}}\]
3. \[\dfrac{{{p_1}{p_2}}}{{4\pi {\varepsilon _ \circ }{x^4}}}\]
4. \[\dfrac{{{p_1}{p_2}}}{{3\pi {\varepsilon _ \circ }{x^4}}}\]
Answer
172.2k+ views
Hint: First, we will need to find the electrostatic field of dipole \[{p_2}\] at \[{p_1}\] . Then we will find the potential energy of two dipoles. In the final step we will differentiate the potential energy to get the Force of interaction between two dipoles.
Complete step-by-step Solution
A dipole is separation of two opposite charges and it is quantified by electric dipole moment and is denoted by p.
As we know electric field of dipole along perpendicular bisector of the axis,
\[\overrightarrow E = - \dfrac{{\overrightarrow p }}{{4\pi {\varepsilon _ \circ }{r^3}}}\] , where r= distance
\[{\varepsilon _ \circ }\] = permittivity of free space
\[{E_{21}}\] is the field due to dipole \[{p_1}\] at dipole \[{p_2}\]
\[{E_{21}} = \dfrac{{{p_1}}}{{4\pi {\varepsilon _ \circ }{x^3}}}\]
Potential energy of dipole system
\[U = - \overrightarrow {{p_2}} .\overrightarrow {{E_{21}}} \]
\[U = - {p_2}\dfrac{{{p_1}}}{{4\pi {\varepsilon _ \circ }{x^3}}}\cos (\pi )\]
Angle between the dipole and electric field is 180 degrees.
\[U = \dfrac{{{p_1}{p_2}}}{{4\pi {\varepsilon _ \circ }{x^3}}}\]
Now, to find the force
\[F = - \dfrac{{dU}}{{dx}} = \dfrac{3}{{4\pi {\varepsilon _ \circ }}}\dfrac{{{p_1}{p_2}}}{{{x^4}}}\]
F is positive, so it is a repulsive force.
Option (1) \[\dfrac{{3{p_1}{p_2}}}{{4\pi {\varepsilon _ \circ }{x^4}}}\]
Additional Information
Electric field due to dipole at a general point
\[E = \dfrac{1}{{4\pi {\varepsilon _ \circ }}}\dfrac{p}{{{r^3}}}\sqrt {3{{\cos }^2}\theta + 1} \] , \[\theta \] =angle between the distance vector and dipole.
Potential due to dipole at a general point
\[V = \dfrac{{p\cos \theta }}{{4\pi {\varepsilon _ \circ }{r^2}}}\]
Note
1. You need to keep in mind the direction of the electric field and dipole.
2. While using the formula of potential energy of dipole, you need to find the angle between field and dipole otherwise you will get the wrong force direction.
3. While finding electric fields, Approximation is made that the length of the dipole is negligible as compared to the distance of the point from the dipole.
Complete step-by-step Solution
A dipole is separation of two opposite charges and it is quantified by electric dipole moment and is denoted by p.
As we know electric field of dipole along perpendicular bisector of the axis,
\[\overrightarrow E = - \dfrac{{\overrightarrow p }}{{4\pi {\varepsilon _ \circ }{r^3}}}\] , where r= distance
\[{\varepsilon _ \circ }\] = permittivity of free space
\[{E_{21}}\] is the field due to dipole \[{p_1}\] at dipole \[{p_2}\]
\[{E_{21}} = \dfrac{{{p_1}}}{{4\pi {\varepsilon _ \circ }{x^3}}}\]
Potential energy of dipole system
\[U = - \overrightarrow {{p_2}} .\overrightarrow {{E_{21}}} \]
\[U = - {p_2}\dfrac{{{p_1}}}{{4\pi {\varepsilon _ \circ }{x^3}}}\cos (\pi )\]
Angle between the dipole and electric field is 180 degrees.
\[U = \dfrac{{{p_1}{p_2}}}{{4\pi {\varepsilon _ \circ }{x^3}}}\]
Now, to find the force
\[F = - \dfrac{{dU}}{{dx}} = \dfrac{3}{{4\pi {\varepsilon _ \circ }}}\dfrac{{{p_1}{p_2}}}{{{x^4}}}\]
F is positive, so it is a repulsive force.
Option (1) \[\dfrac{{3{p_1}{p_2}}}{{4\pi {\varepsilon _ \circ }{x^4}}}\]
Additional Information
Electric field due to dipole at a general point
\[E = \dfrac{1}{{4\pi {\varepsilon _ \circ }}}\dfrac{p}{{{r^3}}}\sqrt {3{{\cos }^2}\theta + 1} \] , \[\theta \] =angle between the distance vector and dipole.
Potential due to dipole at a general point
\[V = \dfrac{{p\cos \theta }}{{4\pi {\varepsilon _ \circ }{r^2}}}\]
Note
1. You need to keep in mind the direction of the electric field and dipole.
2. While using the formula of potential energy of dipole, you need to find the angle between field and dipole otherwise you will get the wrong force direction.
3. While finding electric fields, Approximation is made that the length of the dipole is negligible as compared to the distance of the point from the dipole.
Recently Updated Pages
Sets, Relations, and Functions Mock Test 2025-26

Molarity vs Molality: Definitions, Formulas & Key Differences

Preparation of Hydrogen Gas: Methods & Uses Explained

Polymers in Chemistry: Definition, Types, Examples & Uses

P Block Elements: Definition, Groups, Trends & Properties for JEE/NEET

Order of Reaction in Chemistry: Definition, Formula & Examples

Trending doubts
JEE Main 2025 Session 2: Application Form (Out), Exam Dates (Released), Eligibility, & More

Displacement-Time Graph and Velocity-Time Graph for JEE

Uniform Acceleration

Electric field due to uniformly charged sphere class 12 physics JEE_Main

JEE Main 2025: Derivation of Equation of Trajectory in Physics

Atomic Structure - Electrons, Protons, Neutrons and Atomic Models

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Learn About Angle Of Deviation In Prism: JEE Main Physics 2025

Enthalpy of Combustion with Examples for JEE

Instantaneous Velocity - Formula based Examples for JEE

JEE Advanced Weightage 2025 Chapter-Wise for Physics, Maths and Chemistry

Important Derivations for CBSE Class 12 Physics (Stepwise Solutions & PDF)




