Instantaneous Velocity vs Average Velocity: Key Differences and Graphs
Instantaneous velocity is a foundational concept in JEE Main Physics that describes the rate and direction at which an object changes its position at a particular instant. Unlike average velocity, which considers total displacement over an interval, instantaneous velocity captures the motion at a precise moment—imagine checking a car's speedometer at a single point in time. This concept often appears in JEE questions involving motion analysis, calculus-based derivations, and velocity-time graph problems.
Definition and Meaning of Instantaneous Velocity
In physics, instantaneous velocity is defined as the velocity of an object at a specific instant or point along its path. It is a vector quantity, meaning it has both magnitude (speed at that instant) and direction. This measure captures the real-time motion, making it essential for analyzing non-uniform motion and understanding kinematics in-depth.
A classic real-life example: When you glance at your speedometer while driving, the value you see is the instantaneous velocity (with direction considered). If the needle reads 20 m/s north at that instant, that's your instantaneous velocity.
Instantaneous Velocity Formula and Derivation
The formal definition of instantaneous velocity uses calculus. If s(t) represents displacement as a function of time, then:
- Instantaneous velocity (v) = ds/dt, where ds is an infinitesimal change in displacement and dt is an infinitesimal time interval.
- In limit form: v = limΔt→0 (Δs/Δt)
- Unit: m/s (SI)
Derivation steps for JEE:
- Consider displacement function: s = f(t)
- Average velocity in interval Δt: vavg = (s2 − s1)/(t2 − t1)
- To get instantaneous velocity at time t, shrink Δt to 0: v = limΔt→0 (Δs/Δt) = ds/dt
Here, ds/dt denotes the derivative of displacement with respect to time—a powerful way to analyze motion with calculus, as required in many JEE Main numericals.
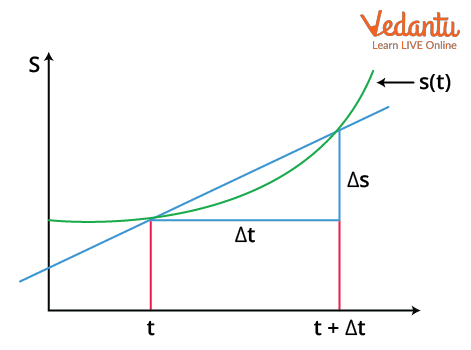
Instantaneous Velocity vs Average Velocity
Students often confuse instantaneous velocity with average velocity. The difference is crucial in JEE, as correct identification determines which formula and approach to use. Here’s a clear comparison:
| Aspect | Instantaneous Velocity | Average Velocity |
|---|---|---|
| Definition | Velocity at a single moment | Total displacement over interval |
| Formula | v = ds/dt | vavg = Δs/Δt |
| Graphical meaning | Slope of tangent at a point | Slope of chord between two points |
| Application | Non-uniform motion, instant analysis | Uniform or net motion, overall result |
For in-depth explanation and visual aids, explore the average velocity formula and difference between speed and velocity.
Graphical Representation and Calculation
On a displacement-time graph, instantaneous velocity at a particular time is the slope of the tangent drawn to the curve at that point. On a velocity-time graph, it is simply the value of velocity at a given instant.
- Identify the specific point of interest (e.g., t = 2 s).
- Draw a tangent to the s–t curve at that point.
- Calculate its slope: (vertical change)/(horizontal change).
- This gives instantaneous velocity at t.
Learn more graph tricks at displacement-velocity-time graphs and get hands-on by practicing at kinematics.
JEE-Style Example: Applying Instantaneous Velocity Formula
Let’s solve a typical JEE Main problem:
- An object moves with displacement s(t) = 3t2 + 2t − 5 (s in m, t in s).
- Find the instantaneous velocity at t = 2 s.
- v = ds/dt = d/dt (3t2 + 2t − 5) = 6t + 2
- At t = 2 s: v = 6×2 + 2 = 14 m/s
The key is differentiating correctly; such calculus applications are frequently tested in JEE.
Common Mistakes and Practical Applications
JEE aspirants should avoid these instant traps with instantaneous velocity:
- Mistaking average for instantaneous velocity—always check if the question asks 'at t = ...'.
- Confusing magnitude with direction; velocity is a vector.
- Wrong slope type on graphs—tangents for instantaneous, chords for average.
- Ignoring sign convention; negative velocity means motion in the opposite direction.
Applications are everywhere: analyzing motion in physics experiments, modelling vehicles' speed changes, and solving critical projectile motion questions for JEE Main. Practicing with differentiation in kinematics sharpens skills in solving advanced problems.
Practice Problems on Instantaneous Velocity
- If s(t) = 4t3 − 2t, find the instantaneous velocity at t = 1 s.
- An object’s velocity-time graph shows a straight line. What does constant instantaneous velocity indicate?
- Calculate the instantaneous velocity at t = 0 for s(t) = 5 − t2.
- A car changes its direction but maintains the same speed. What happens to its instantaneous velocity vector?
- If the instantaneous velocity is zero at some point, what can you say about motion at that instant?
For detailed solutions and more practice, check out kinematics mock test and kinematics practice papers.
Need a deeper dive? Explore motion in one dimension, revisit Laws of Motion, and strengthen your calculus base at differentiation in kinematics. Vedantu, trusted by lakhs of JEE aspirants, offers concepts, mock tests, and revision robustly mapped to JEE Physics requirements.
FAQs on Instantaneous Velocity in Physics: Meaning, Formula, and Applications
1. What is instantaneous velocity?
Instantaneous velocity is the velocity of an object measured at a specific instant or point in time. It describes both the speed and direction of motion at that moment.
Key points include:
- It is a vector quantity (has direction and magnitude).
- Defined as the rate of change of displacement at a given instant.
- Mathematically, it is the derivative of displacement with respect to time (v = ds/dt).
- Reflects the speedometer reading at a specific time.
2. What is the formula for instantaneous velocity?
The instantaneous velocity formula gives the velocity at a particular moment:
v = ds/dt
- Where v = instantaneous velocity
- ds = small change in displacement
- dt = small change in time
3. How is instantaneous velocity different from average velocity?
While both measure how fast an object moves, the difference lies in the time considered:
- Average velocity: Total displacement divided by total time taken (covers the entire journey).
- Instantaneous velocity: Velocity at a specific instant or point in time.
4. How do you determine instantaneous velocity from a graph?
You can find instantaneous velocity from a graph in these ways:
- On a displacement-time graph: It equals the slope of the tangent at a given point.
- On a velocity-time graph: The value of the graph directly gives the instantaneous velocity at that time.
5. What is the symbol and SI unit for instantaneous velocity?
The standard symbol for instantaneous velocity is v, and its SI unit is metres per second (m/s). This is the same as for average velocity because both measure the rate of motion, but at different time scales.
6. Can instantaneous velocity ever be negative? If so, what does it mean?
Yes, instantaneous velocity can be negative. A negative value indicates the object is moving in the direction opposite to the chosen positive direction.
- If the reference direction is right, a negative velocity means motion to the left.
- Only the direction changes — the speed (magnitude) is always positive.
7. What is the formula for instantaneous velocity using calculus?
Using calculus, instantaneous velocity is defined as the derivative of displacement (s) with respect to time (t):
v = ds/dt
This formula finds how fast and in what direction displacement changes at any instant.
8. Does an object at rest have any instantaneous velocity?
When an object is at rest, its instantaneous velocity is zero.
- No change in position means zero velocity at every instant during rest.
9. Why is average velocity sometimes inappropriate to use in numericals?
Average velocity only considers total displacement over total time, which can miss critical details in motion that involves changes in speed or direction.
- It does not reflect variations at specific moments.
- For problems involving acceleration or non-uniform motion, instantaneous velocity is needed for accurate solutions.
10. How do you apply the formula for instantaneous velocity in numerical problems?
To apply the instantaneous velocity formula:
- Write the displacement equation as a function of time, s(t).
- Differentiate s(t) with respect to t (find ds/dt).
- Substitute the required time value into the derivative to get v.
