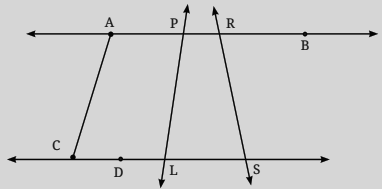
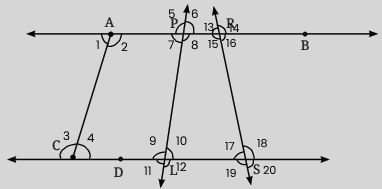
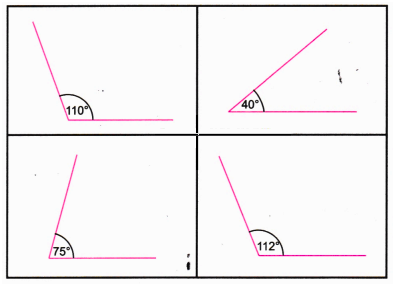
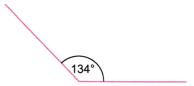
Class 6 Maths Chapter 2 Questions and Answers - Free PDF Download
In Ncert Solutions Class 6 Maths Chapter 2 Exercise 2 10, you’ll learn how to draw and measure angles using a protractor and compass. This part of geometry can feel tricky at first, but once you get the hang of it, you’ll find drawing angles much easier and even fun!
Table of Content
These NCERT Solutions make every step super simple, so you never have to feel confused if your angle doesn’t look right. With clear instructions and helpful tips from Vedantu, you can practice as much as you want by downloading the free PDF. If you want to see the full syllabus for your class, check out the official Class 6 Maths syllabus to see how this topic fits in.
Practising these questions from the NCERT Solutions will build your confidence and help you score better in geometry questions during your exams.
Exercise 2.10
1. In Fig, list all the angles possible. Did you find them all? Now, guess the measures of all the angles. Then, measure the angles with a protractor. Record all your numbers in a table. See how close your guesses are to the actual measures.
Ans: In the figure, we can list the 20 angles based on the intersections of the lines. Here's how to proceed:
Based on a guess, we estimate that ∠1 = ∠4 = 60° and ∠2 = ∠3 = 120°.
However, after measuring, the actual values turn out to be ∠1 = ∠4 = 70° and ∠2 = ∠3 = 110°.
This shows that while our initial guesses were close, the precise measurements gave a slightly different result, emphasising the importance of using a protractor for accuracy.
2. Use a protractor to draw angles having the following degree measures:
a. 110°
b. 40°
c. 75°
d. 112°
e. 134°
Ans:
3. Draw an angle whose degree measure is the same as the angle given below:
Also, write down the steps you followed to draw the angle.
Ans:
Step 1: Begin by measuring the given angle ∠IHJ, which is 120°, using a protractor. Ensure the protractor is aligned properly with the ray HJ for accuracy.
Step 2: Using the protractor, draw a new angle, ∠ABC, that also measures 120°. Align the protractor with point B and mark the angle accurately to match the original one.
Benefits of NCERT Solutions for Class 6 Chapter 2 Lines and Angles Exercise 2.10
The solutions provide step-by-step instructions for drawing angles, making it easy for students to follow along and understand the process.
The inclusion of diagrams and visuals helps students see the steps involved in measuring and constructing angles accurately.
Various practice problems allow students to apply what they have learned, reinforcing their skills in drawing different types of angles.
The solutions include real-life examples that show the importance of angles, helping students relate their learning to everyday situations.
By practising drawing angles, students gain confidence in using tools like a compass and a protractor, which are essential for geometry.
Understanding how to draw angles lays a strong foundation for more advanced geometry topics, preparing students for future lessons.
Class 6 Maths Chapter 2: Exercises Breakdown
Important Study Material Links for Class 6 Maths Chapter 2 - Lines and Angles
Conclusion
NCERT Solutions for Class 6 Maths Chapter 2, Exercise 2.10, "Lines and Angles," helps students learn how to accurately draw angles in geometry. The clear explanations in the solutions make it easier for students to use a protractor and compass for creating different angles. Practising these exercises improves student’s understanding of angles, which is important for learning more advanced geometric concepts. With the solutions available as a FREE PDF download, students can study and review at their own pace, making learning both convenient and effective.
Chapter-wise NCERT Solutions Class 6 Maths
The chapter-wise NCERT Solutions for Class 6 Maths are given below. Go through these chapter-wise solutions to be thoroughly familiar with the concepts.
Related Important Links for Class 6 Maths
Along with this, students can also download additional study materials provided by Vedantu for Maths Class 6.
FAQs on NCERT Solutions For Class 6 Maths Chapter 2 Lines And Angles Exercise 2.10 - 2025-26
1. How do the NCERT Solutions for Class 6 Maths Chapter 2 explain finding the successor and predecessor of a whole number?
The NCERT Solutions provide a clear, step-by-step method. To find the successor of a whole number, you simply add 1 to it (e.g., the successor of 99 is 99 + 1 = 100). To find the predecessor, you subtract 1 from the number (e.g., the predecessor of 100 is 100 - 1 = 99). The solutions emphasise that the whole number 0 does not have a whole number predecessor.
2. What is the step-by-step method to show the addition of whole numbers on a number line as per the NCERT solutions for Chapter 2?
The NCERT Solutions for Class 6 Maths explain this visual method as follows:
First, draw a straight line and mark points at equal intervals, labelling them 0, 1, 2, 3, and so on. This is your number line.
To add two numbers, say 3 and 4, start at the first number (3) on the number line.
Move a number of steps equal to the second number (4) to the right. From 3, moving 4 steps right will land you on 7.
Therefore, the solution is 3 + 4 = 7. This method helps in visualising the concept of addition.
3. Why is zero considered the additive identity for whole numbers in the NCERT syllabus?
Zero is called the additive identity because when it is added to any whole number, the value of that number does not change. The NCERT solutions demonstrate this with examples like 5 + 0 = 5 and 0 + 17 = 17. This unique property of zero makes it a special element in the set of whole numbers, serving as a neutral element for the addition operation.
4. How do the NCERT Solutions demonstrate that whole numbers are not closed under subtraction and division?
The solutions prove this using counter-examples. For subtraction, if you subtract a larger number from a smaller one (e.g., 5 - 8), the result is -3, which is an integer but not a whole number. For division, dividing 5 by 2 gives 2.5, which is not a whole number. Since the result of these operations is not always a whole number, the solutions conclude that whole numbers are not closed under subtraction and division.
5. What is the correct way to solve problems using the distributive property as detailed in Class 6 Maths Chapter 2 solutions?
The NCERT solutions explain the distributive property of multiplication over addition to simplify calculations. For an expression like 12 × 105, instead of direct multiplication, you can break 105 into (100 + 5). The problem becomes (12 × 100) + (12 × 5), which simplifies to 1200 + 60 = 1260. This method, clearly shown in the solutions, makes mental maths easier and is crucial for solving complex problems efficiently.
6. How does applying the associative property, as shown in the NCERT solutions, make calculations with large whole numbers simpler?
The associative property allows you to regroup numbers in an addition or multiplication problem to make calculations easier. For example, to solve 25 + 68 + 75, the NCERT solutions suggest regrouping it as (25 + 75) + 68. This simplifies to 100 + 68 = 168, which is much easier to calculate than adding in the original order. This shows how understanding properties is not just theoretical but a practical tool for problem-solving.
7. According to the NCERT solutions, what is the significance of '1' in the multiplication of whole numbers?
In the NCERT framework, the number '1' is known as the multiplicative identity for whole numbers. This is because any whole number multiplied by 1 results in the number itself (e.g., 25 × 1 = 25). The solutions highlight this property to establish the foundational rules of multiplication and its relationship with other operations like division.
8. What is the key difference between a 'whole number' and a 'natural number' as defined in Chapter 2 of the NCERT textbook?
The NCERT solutions clarify a fundamental difference: Natural numbers are the counting numbers starting from 1 (1, 2, 3, ...). Whole numbers include all the natural numbers plus the number zero (0, 1, 2, 3, ...). Therefore, the only whole number that is not a natural number is 0. All natural numbers are also whole numbers.
