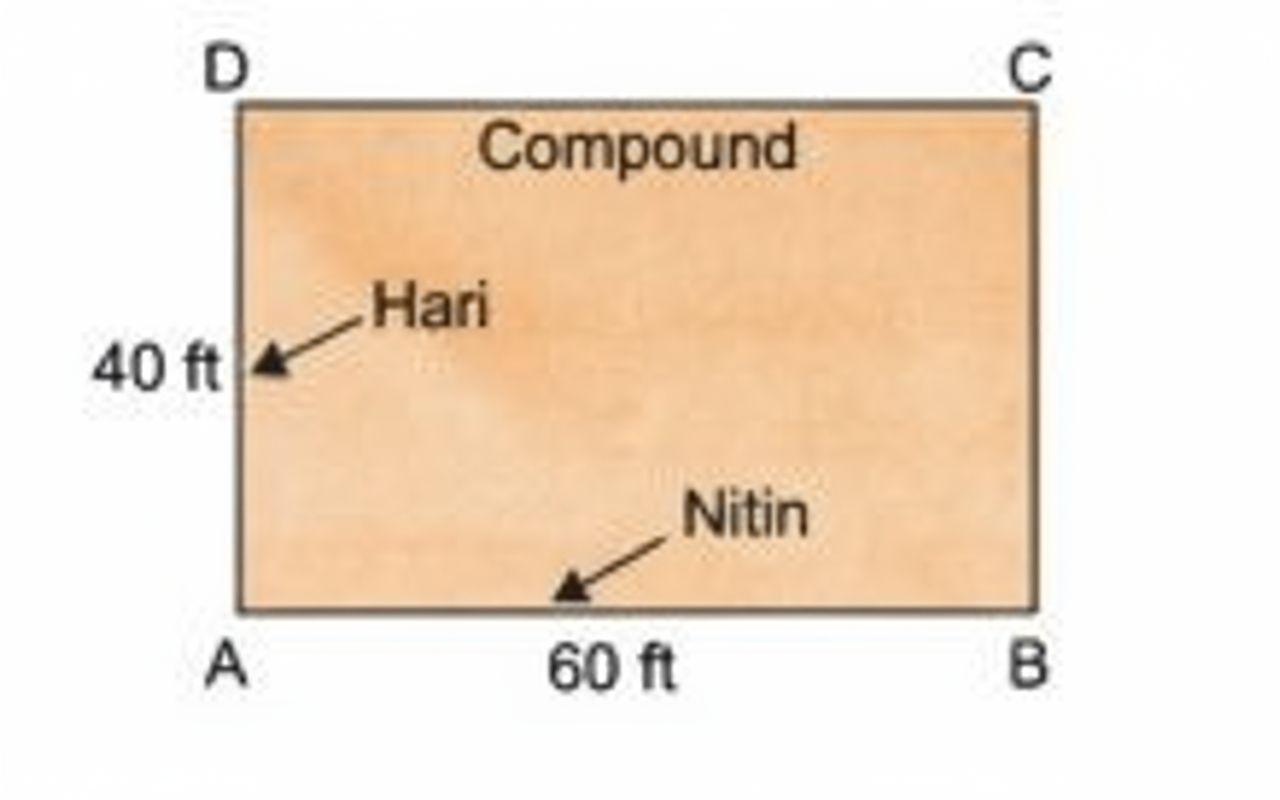
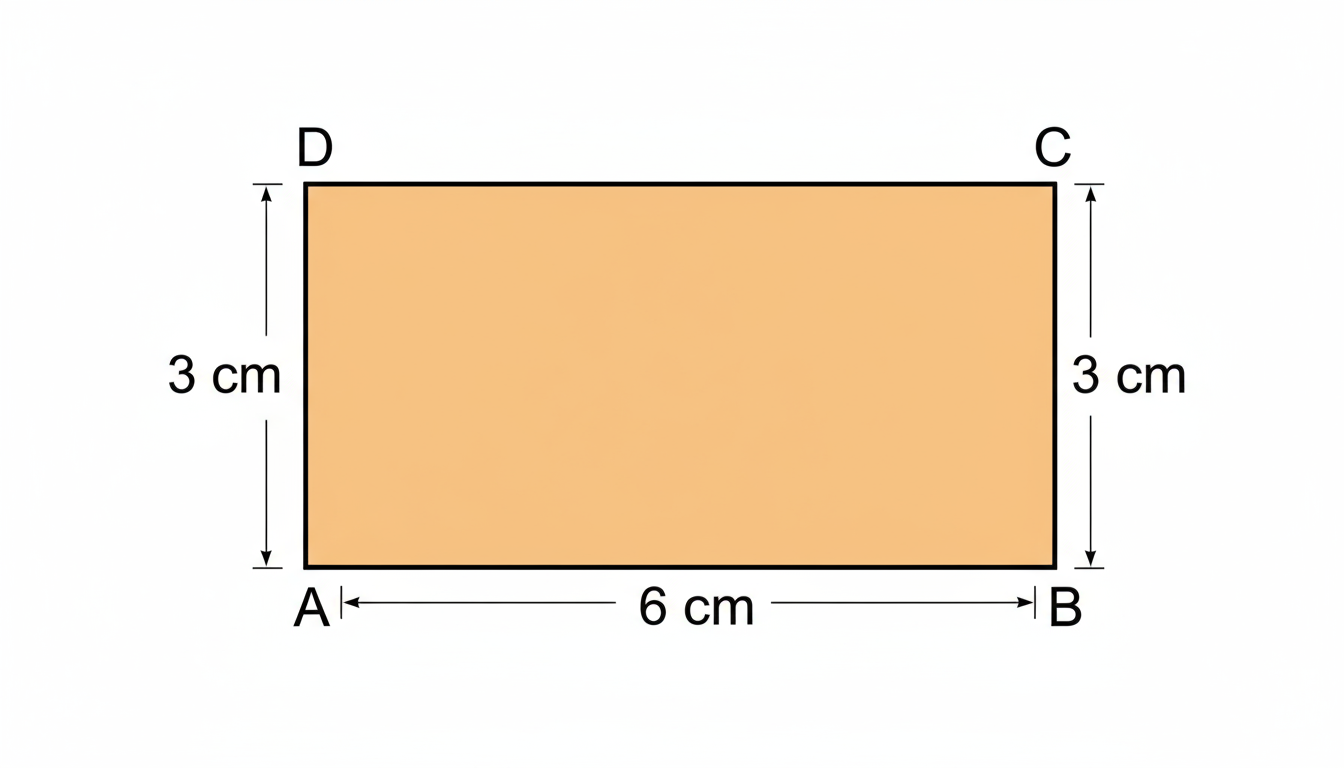
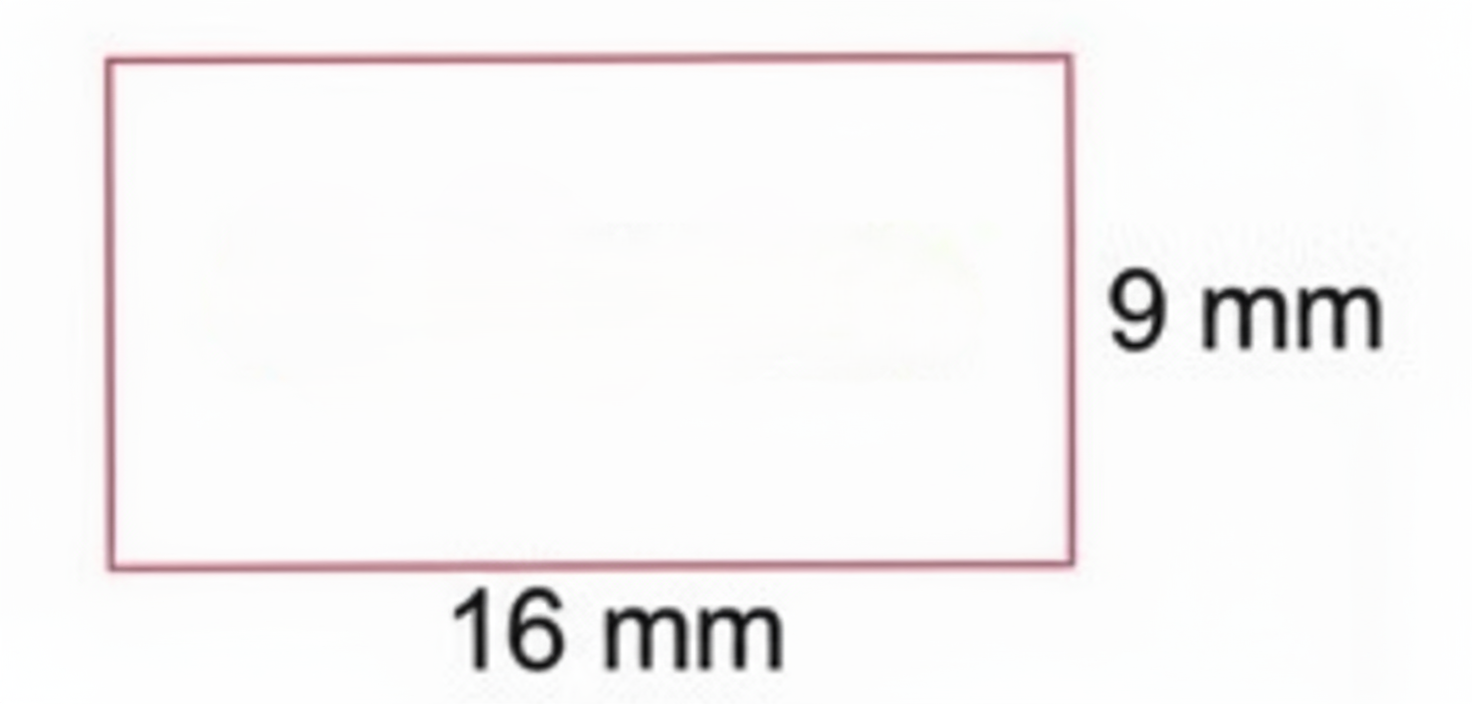
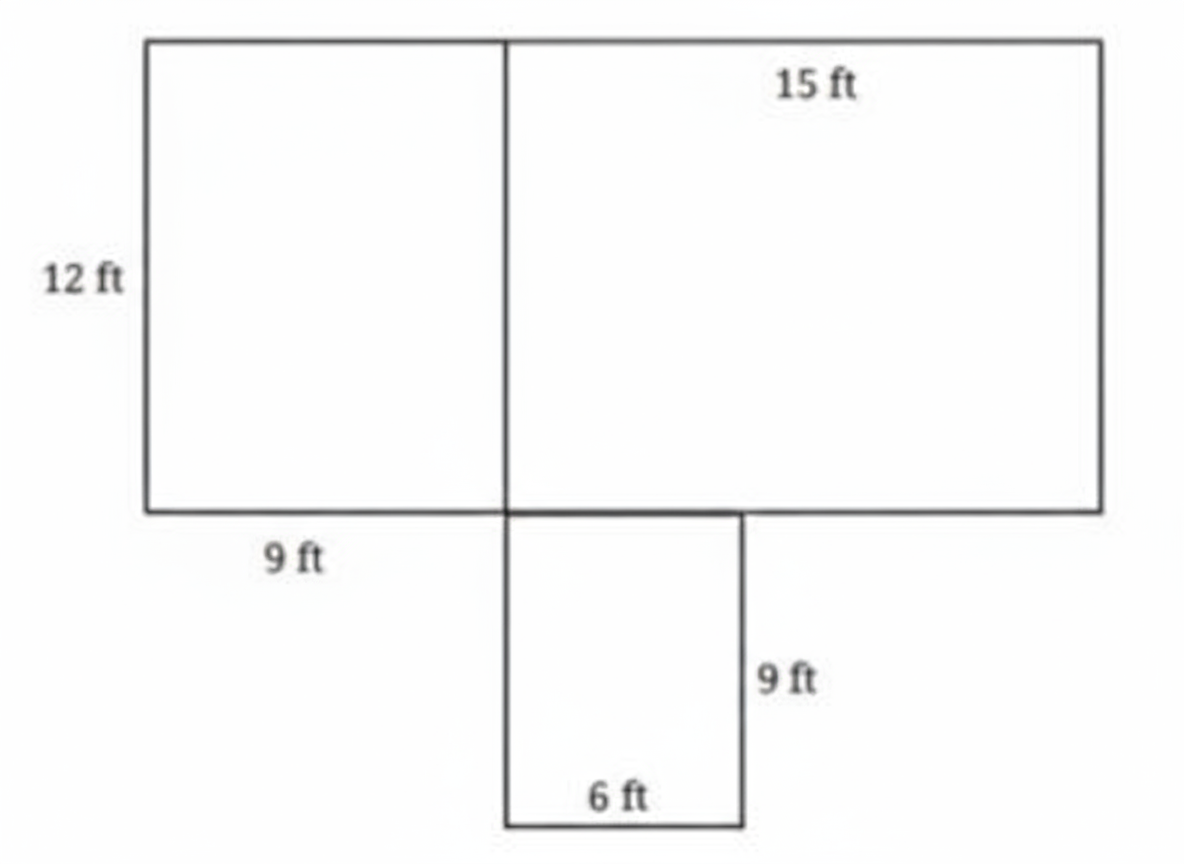
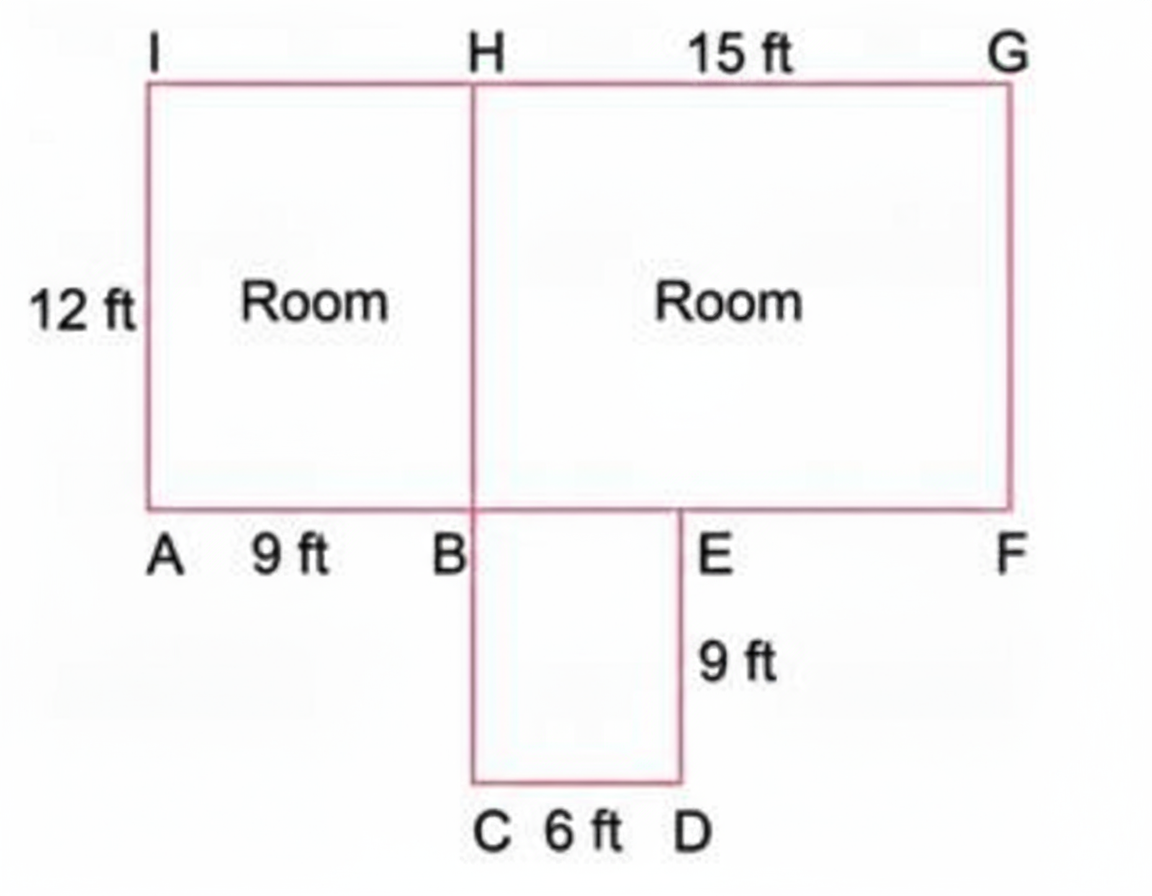
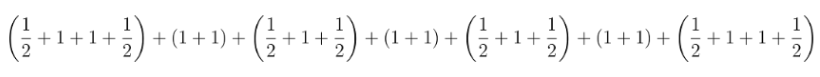How to Write Stepwise Solutions for Proportional Reasoning in Class 8 Maths
FAQs on NCERT Solutions For Class 8 Maths Chapter 7 Proportional Resoning - I (2025-26)
1. What are NCERT Solutions for Class 8 Maths Chapter 7 Proportional Reasoning - I, and why are they important for CBSE exams?
NCERT Solutions for Class 8 Maths Chapter 7 Proportional Reasoning - I provide detailed, stepwise answers to all textbook exercises, fully aligned with the CBSE 2025–26 pattern. Using these Vedantu solutions is crucial, as they help you understand proportional reasoning concepts, reinforce exam-style answering, and ensure scoring full marks by following the exact marking scheme recommended by CBSE.
2. How can I use Vedantu's NCERT Solutions for Class 8 Maths Chapter 7 to master stepwise answers and score full marks?
To score full marks in CBSE exams, practicing stepwise answers from Vedantu's NCERT Solutions for Class 8 Maths Chapter 7 Proportional Reasoning - I is highly effective.
- Read the question and understand all requirements before starting.
- Write each calculation and step in sequence, explaining logic when necessary.
- Highlight key formulae and final answers.
- Ensure neat presentation, as per CBSE patterns.
- Cross-check your answers with Vedantu's model solutions for accuracy.
3. Where can I download the exercise-wise PDF of NCERT Solutions for Class 8 Maths Chapter 7 Proportional Reasoning - I for free?
You can freely access and download the exercise-wise PDF of NCERT Solutions for Class 8 Maths Chapter 7 Proportional Reasoning - I directly from Vedantu. These downloadable PDFs are updated for the latest CBSE syllabus so you can prepare effectively offline whenever needed.
4. Are diagrams or definitions mandatory in NCERT Solutions for Class 8 Maths Chapter 7 Proportional Reasoning - I?
Including clear definitions and neat diagrams in your NCERT Solutions for Class 8 Maths Chapter 7 Proportional Reasoning - I often adds value and helps secure additional marks. For questions requiring explanations, precise definitions ensure accuracy, while properly labelled diagrams demonstrate understanding, following CBSE guidelines.
5. What are the most important topics and definitions in NCERT Solutions for Class 8 Maths Chapter 7 Proportional Reasoning - I?
Understanding the important topics in NCERT Solutions for Class 8 Maths Chapter 7 Proportional Reasoning - I is essential for board exams. Key areas include:
- Definition and identification of proportions.
- Solving direct and inverse proportion problems.
- Application of ratios in real-life scenarios.
- Stepwise solutions for word problems.
6. How should I structure long answers for NCERT Solutions for Class 8 Maths Chapter 7 to align with the CBSE marking scheme?
To align long answers with the CBSE marking scheme using NCERT Solutions for Class 8 Maths Chapter 7 Proportional Reasoning - I, follow these steps:
- Write a brief introduction or definition relevant to the topic.
- Break the answer into logical steps, clearly explaining each calculation or reasoning.
- Support your solution with diagrams or examples when asked.
- Conclude with the final answer, highlighting it as per CBSE practice.
7. Do examiners award partial marks for correct steps in NCERT Solutions for Class 8 Maths Chapter 7, even if the final answer is incorrect?
CBSE examiners generally award partial marks if your steps and approach in NCERT Solutions for Class 8 Maths Chapter 7 Proportional Reasoning - I are correct, even if the final answer is wrong. Demonstrating the right procedure and logical progression can help maximize your score according to the CBSE step-marking policy.
8. How can I revise NCERT Solutions for Class 8 Maths Chapter 7 Proportional Reasoning - I quickly before exams?
Efficient revision of NCERT Solutions for Class 8 Maths Chapter 7 Proportional Reasoning - I is possible with a structured plan:
- Review Vedantu's quick notes and summary sheets daily.
- Practice important exercise questions and formulas.
- Attempt sample and previous years' questions for exam-style experience.
- Use flashcards or a 1-day to 7-day planner for timed revisions before tests.
9. What are common mistakes to avoid in NCERT Solutions for Class 8 Maths Chapter 7 Proportional Reasoning - I?
Avoiding common errors in NCERT Solutions for Class 8 Maths Chapter 7 Proportional Reasoning - I helps you score better:
- Do: Read each question twice, show all steps, and check ratios and units.
- Don't: Skip definitions, ignore diagram labels, or leave calculation steps unexplained.
10. Are NCERT Solutions for Class 8 Maths Chapter 7 Proportional Reasoning - I on Vedantu sufficient for exam preparation?
For most CBSE school exams, Vedantu's NCERT Solutions for Class 8 Maths Chapter 7 Proportional Reasoning - I are comprehensive and strictly follow the syllabus. However, for complete mastery, combine them with regular practice, Vedantu's revision sets, and exemplar problems to handle advanced or application-based questions by the board.
11. How do I label diagrams and present maps in NCERT Solutions for Class 8 Maths Chapter 7 Proportional Reasoning - I to secure easy marks?
Neately labelled diagrams and maps in NCERT Solutions for Class 8 Maths Chapter 7 Proportional Reasoning - I are rewarded by CBSE evaluators. Use pencils for diagrams, write labels outside figures, keep lines straight, and use correct conventions as shown in Vedantu's solutions to maximize your score for presentation.
12. Are references to textbook page numbers helpful when revising Vedantu NCERT Solutions for Class 8 Maths Chapter 7?
Including textbook page numbers while revising Vedantu NCERT Solutions for Class 8 Maths Chapter 7 Proportional Reasoning - I helps you quickly locate explanations, cross-reference concepts, and ensure you don't miss important intext or back exercise problems during exam prep.