Maths Class 12 Chapter 12 Questions and Answers - Free PDF Download
In NCERT Solutions Class 12 Maths Chapter 12 Exercise 12 1, you’ll explore how to solve real-world problems using the basics of Linear Programming. This chapter teaches you how to make simple graphs and use them to find the best answers for problems with limits or restrictions. If you ever felt confused about objective functions, constraints, or feasible regions, this exercise will make these ideas easy to understand step by step.
Table of Content
With Vedantu’s clear solutions and easy-to-download PDF, you’ll get detailed explanations for every question, so you can prepare better for your CBSE board exams. If you want to brush up on the full curriculum, check out the Class 12 Maths Syllabus too.
These NCERT Solutions will help you practise important exam questions and boost your confidence with each attempt. There’s even a quick link to all Class 12 Maths NCERT Solutions for easy access whenever you need a hand.
Exercise 12.1
1: Maximise $Z=3x+4y$
Subject to the constraints: $x+y\ge 4$, $x\ge 0$, $y\ge 0$
Ans: The constraints: $x+y\ge 4$, $x\ge 0$, and $y\ge 0$, determine the feasible region as shown below:
The values of $Z$at the corner points $O(0,0),A(4,0),B(0,4)$ of the feasible region are:
Hence, the maximum value of $Z$ is $16$ at the point $B(0,4)$.
2: Minimise $Z=3x+4y$.
Subject to constraints $x+2y\le 8$, $3x+3y\le 12$,$x\ge 0$ and $y\ge 0$.
Ans: The constraints $x+2y\le 8$, $3x+3y\le 12$,$x\ge 0$ and $y\ge 0$ determine the feasible region as shown below:
The values of $Z$at the corner points $O(0,0),A(4,0),B(2,3)$ and $C(0,4)$ of the feasible region are:
Hence, the minimum value of $Z$ is $-12$ at the point $A(4,0)$.
3: Maximise $Z=5x+3y$
Subject to the constraints: $3x+5y\le 15$, $5x+2y\le 10$, $x\ge 0$, $y\ge 0$
Ans: The constraints: $3x+5y\le 15$, $5x+2y\le 10$,$x\ge 0$, and $y\ge 0$ determine the feasible region as shown below:
The values of $Z$at the corner points $O(0,0),A(2,0),B(0,3)$ and $C(\frac{20}{19},\frac{45}{19})$ of the feasible region are:
Hence, the maximum value of $Z$ is $\frac{235}{19}$ at the point$C(\frac{20}{19},\frac{45}{19})$.
4: Minimise $Z=3x+5y$
Subject to the constraints: $x+3y\ge 3$, $x+y\ge 2$, $x\ge 0$, $y\ge 0$
Ans: The constraints $x+3y\ge 3$, $x+y\ge 2$,$x\ge 0$, and $y\ge 0$ determine the feasible region as shown below:
Therefore, the feasible region is unbounded.
The values of $Z$at the corner points $A(3,0),B(\frac{3}{2},\frac{1}{2})$ and $C(0,2)$ of the feasible region are:
Since, the feasible region is unbounded, $7$ may or may not be the minimum value of $Z$.
So, we draw the graph of the inequality, $3x+5y<7$, and check if the resulting half-plane has common points with the feasible region.
As the feasible region has no common point with $3x+5y<7$, the minimum value of $Z$ is $7$ at the point $B(\frac{3}{2},\frac{1}{2})$.
5: Maximise $Z=3x+2y$
Subject to the constraints: $x+2y\le 10$, $3x+5y\le 15$, $x\ge 0$, $y\ge 0$
Ans: The constraints, $x+2y\le 10$, $3x+5y\le 15$,$x\ge 0$, and $y\ge 0$ determine the feasible region as shown below:
The values of $Z$at the corner points $A(5,0),B(4,3)$ and $C(0,5)$ of the feasible region are:
Hence, the maximum value of $Z$ is $18$ at the point $B(4,3)$.
6: Minimise $Z=x+2y$
Subject to the constraints: $2x+y\ge 8$, $x+2y\ge 6$, $x\ge 0$, $y\ge 0$
Ans: The constraints $2x+y\ge 8$, $x+2y\ge 6$,$x\ge 0$, and $y\ge 0$ determine the feasible region as shown below:
The values of $Z$at the corner points $A(6,0)$ and $B(0,3)$ of the feasible region are:
As the value of $Z$ at points $A(6,0)$ and $B(0,3)$ is same, we need to take any other point, for example, $(2,2)$ on line $x+2y=6$
Now, $Z=6$ .
Thus, the minimum value of $Z$ occurs at more than $2$ points. Hence, we can say that the value of $Z$ is minimum at every point on the line $x+2y=6$.
7: Minimise and Maximise $Z=5x+10y$
Subject to the constraints: $x+2y\le 120$, $x+y\ge 60$, $x-2y\ge 60$,$x\ge 0$, $y\ge 0$
Ans: The constraints $x+2y\le 120$, $x+y\ge 60$,$x-2y\ge 60$, $x\ge 0$, and $y\ge 0$ determine the feasible region as shown below:
The values of $Z$at the corner points $A(60,0),B(120,0),C(60,30)$ and $D(40,20)$ of the feasible region are:
Hence, the minimum value of $Z$ is $300$ at the point $A(60,0)$and the maximum value of $Z$ is $600$ at all the points lying on the line segment joining the points $B(120,0)$ and $C(60,30)$.
8: Minimise and Maximise $Z=x+2y$
Subject to the constraints: $x+2y\ge 100$, $2x-y\le 0$, $2x+y\le 200$,$x\ge 0$, $y\ge 0$
Ans: The constraints $x+2y\ge 100$, $2x-y\le 0$,$2x+y\le 200$, $x\ge 0$, and $y\ge 0$ determine the feasible region as shown below:
The values of $Z$at the corner points $A(0,50),B(20,40),C(50,100)$ and $D(0,200)$ of the feasible region are:
Hence, the maximum value of $Z$ is $400$ at the point $D(0,200)$and the minimum value of $Z$is $100$ at all the points lying on the line segment joining the points $A(0,50)$ and $B(20,40)$.
9: Maximise $Z=-x+2y$
Subject to the constraints: $x\ge 3$, $x+y\ge 5$, $x+2y\ge 6$ , $y\ge 0$
Ans: The constraints $x\ge 3$, $x+y\ge 5$,$x+2y\ge 6$, and $y\ge 0$ determine the feasible region as shown below:
It is visible that the feasible region is unbounded.
The values of $Z$ at corner points $A(6,0),B(4,1)$ and $C(3,2)$are given as:
Since, the feasible region is unbounded, $Z=1$ may or may not be the maximum value.
So, we will draw the graph of the inequality, $-x+2y>1$, and check if the resulting half-plane has common points with the feasible region.
As the resulting feasible region has common points with the feasible region. Therefore, $Z=1$ is not the maximum value. Also, $Z$ has no maximum value.
10: Maximise $Z=x+y$
Subject to the constraints: $x-y\le -1$, $-x+y\le 0$, $x\ge 0$ , and $y\ge 0$
Ans: The constraints, $x-y\le -1$, $-x+y\le 0$,$x\ge 0$, and $y\ge 0$ determine the feasible region as shown below:
It can be seen that there is no feasible region. Thus, $Z$ does not have any maximum value.
Conclusion
Exercise 12.1 of Chapter 12 in Class 12 Maths is essential for mastering linear programming. This exercise focuses on formulating linear programming problems, using the graphical method to solve them, and identifying feasible and optimal solutions. Understanding objective functions, constraints, and the feasible region is crucial. Vedantu's NCERT Solutions offer clear, step-by-step guidance, helping students grasp these concepts effectively. Practicing these solutions will enhance problem-solving skills and exam readiness. Concentrate on the graphical method and evaluating objective functions at corner points for optimal solutions.
CBSE Class 12 Maths Chapter 12 Other Study Materials
NCERT Solutions for Class 12 Maths | Chapter-wise List
Given below are the chapter-wise NCERT 12 Maths solutions PDF. Using these chapter-wise class 12th maths ncert solutions, you can get clear understanding of the concepts from all chapters.
Related Links for NCERT Class 12 Maths in Hindi
Explore these essential links for NCERT Class 12 Maths in Hindi, providing detailed solutions, explanations, and study resources to help students excel in their mathematics exams.
Important Related Links for NCERT Class 12 Maths
FAQs on NCERT Solutions For Class 12 Maths Chapter 12 Linear Programming Exercise 12.1 - 2025-26
1. What are the key steps to solve a Linear Programming Problem (LPP) from NCERT Class 12 Maths Chapter 12 for the 2025-26 session?
To solve an LPP using the NCERT method, you must follow these sequential steps:
- First, identify the decision variables (e.g., x and y) and define the objective function (e.g., Z = ax + by) which needs to be maximised or minimised.
- Formulate all the given limitations as linear inequalities, which are known as constraints.
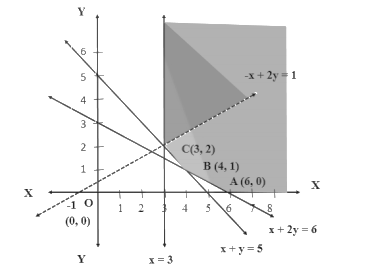
- Graph each linear inequality, treating it as an equation to draw the boundary line. Shade the solution region for each constraint.
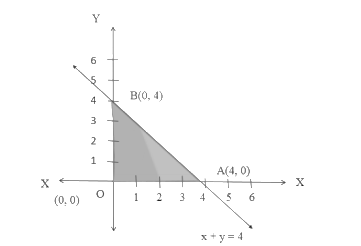
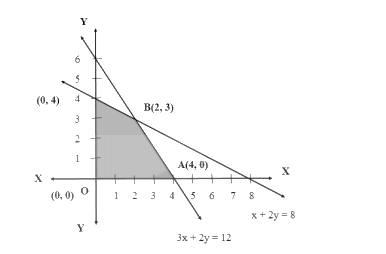
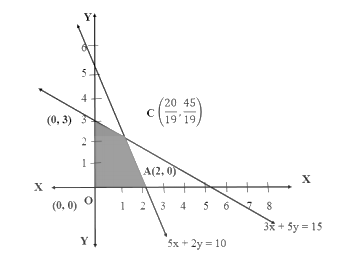
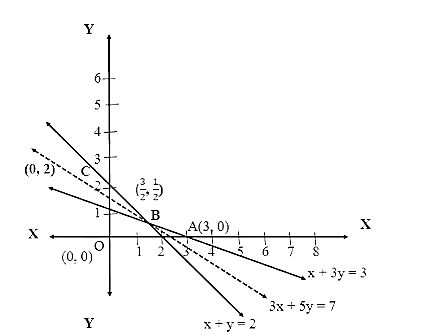
- Identify the feasible region, which is the common area that satisfies all constraints simultaneously.
- Determine the coordinates of all corner points (vertices) of the feasible region.
- Substitute the coordinates of each corner point into the objective function to find its value at each point.
- The largest or smallest value of Z is the optimal solution, depending on whether the goal is maximisation or minimisation.
2. How do you correctly identify the feasible region when solving an LPP graphically?
The feasible region is the area on the graph that represents all possible solutions to the problem. To identify it correctly:
- Plot the line for each constraint. Use a solid line for inequalities with ≤ or ≥ and a dashed line for < or >.
- For each constraint line, pick a test point (usually the origin, (0,0), if it's not on the line) to determine which side of the line satisfies the inequality.
- Shade the half-plane that contains the valid solutions for that constraint.
- The feasible region is the overlapping or common shaded area that satisfies all the constraints at the same time. This region can be either bounded (a closed polygon) or unbounded.
3. What is the role of an objective function and constraints in solving NCERT questions on Linear Programming?
In Linear Programming, these two components are fundamental:
- The Objective Function (e.g., Z = 3x + 4y) is a linear expression that represents the quantity you want to optimise—either maximise (like profit) or minimise (like cost). The entire problem is solved to find the optimal value of Z.
- Constraints (e.g., x + y ≤ 4) are the set of linear inequalities that represent the limitations or restrictions in the problem, such as limits on resources, time, or materials. They define the boundaries of the feasible region.
4. How does the NCERT method for finding the optimal solution differ between a bounded and an unbounded feasible region?
The approach changes significantly based on the type of feasible region:
- For a bounded feasible region, the optimal solution (both maximum and minimum) is guaranteed to exist and will always be found at one of its corner points (vertices). You simply test all corner points in the objective function to find the optimal value.
- For an unbounded feasible region, an optimal solution may or may not exist. After finding the maximum or minimum value at the corner points, you must perform an additional verification step. For example, to verify a minimum value 'm', you must graph the inequality ax + by < m and check if it has any common points with the feasible region. If there are no common points, 'm' is the minimum value; otherwise, no minimum value exists.
5. In some NCERT problems, the optimal solution occurs at more than one point. How do you identify and describe the solution in such cases?
This happens when the objective function's slope is the same as the slope of one of the boundary lines of the feasible region. If you calculate the value of Z at all corner points and find that two adjacent corner points yield the same optimal value (e.g., the same maximum profit), it means there are multiple solutions. The correct way to state the answer is that the optimal value occurs at every point on the line segment connecting these two corner points.
6. Why is it crucial to test all corner points of the feasible region when solving an LPP? What common errors does this prevent?
It is crucial because the Corner Point Theorem, a fundamental principle of Linear Programming, states that if an optimal solution exists, it must occur at a vertex (or corner point) of the feasible region. Testing all corner points guarantees that you find the absolute maximum or minimum value as required by the problem. This systematic approach prevents the common error of prematurely stopping after finding one value that seems high or low, or incorrectly guessing the optimal point just by looking at the graph, which can lead to an incorrect answer.
7. What is the correct interpretation if the constraints in a Linear Programming Problem do not form a feasible region?
If the shaded regions for all the linear inequalities (constraints) do not have any area in common, it means there is no feasible region. This indicates that there are no possible solutions that can satisfy all the given conditions of the problem simultaneously. Therefore, the LPP has no solution, and you cannot find a maximum or minimum value for the objective function Z.
8. What is the main difference between an objective function and a constraint in the context of Class 12 Maths Chapter 12?
The main difference lies in their purpose. The objective function is what you aim to optimise (maximise or minimise), representing the goal of the problem (e.g., Z = Profit). A constraint is a rule or limitation that you must obey, which restricts the possible values of your variables (e.g., resource availability). In short, the objective function sets the goal, while the constraints define the rules of the game.
