Class 10 Maths Chapter 3 Exercise 3.1 Pair Of Linear Equations In Two Variables Question Answers Explained
NCERT Solutions For Class 10 Maths Chapter 3 Pair Of Linear Equations In Two Variables Exercise 3.1 (2025-26)
FAQs on NCERT Solutions For Class 10 Maths Chapter 3 Pair Of Linear Equations In Two Variables Exercise 3.1 (2025-26)
1. What is the method followed in NCERT Solutions for Class 10 Maths Chapter 3 Exercise 3.1 to solve a pair of linear equations graphically?
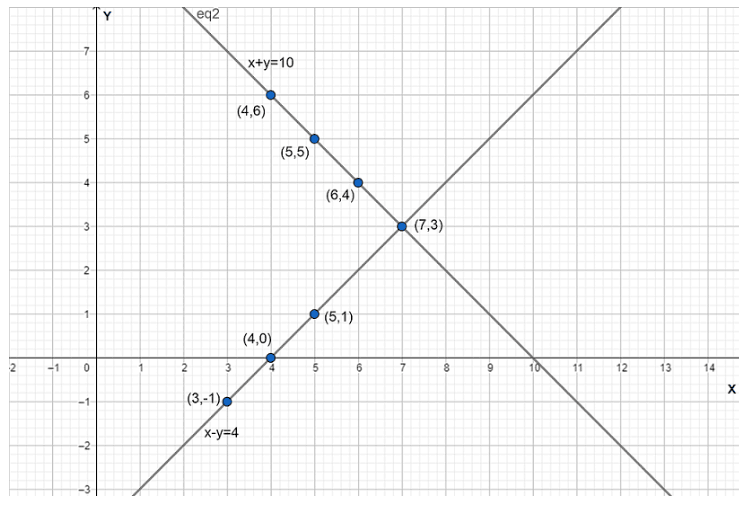
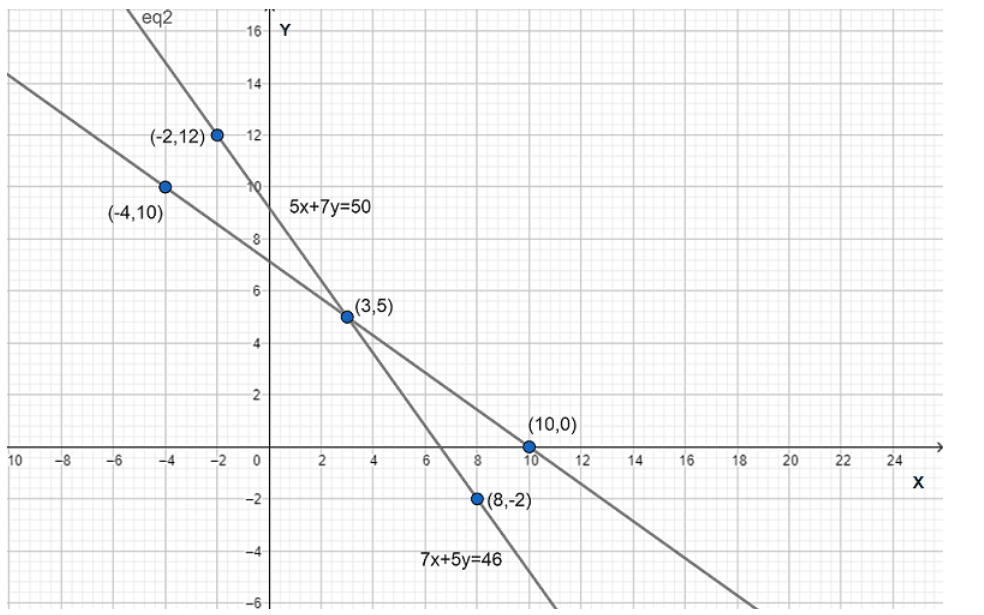
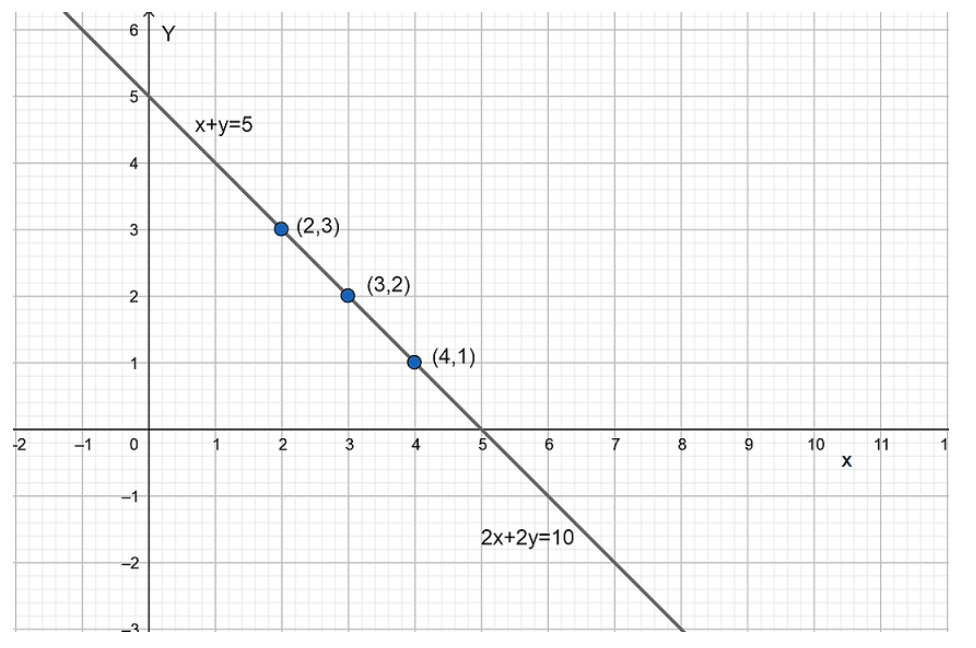
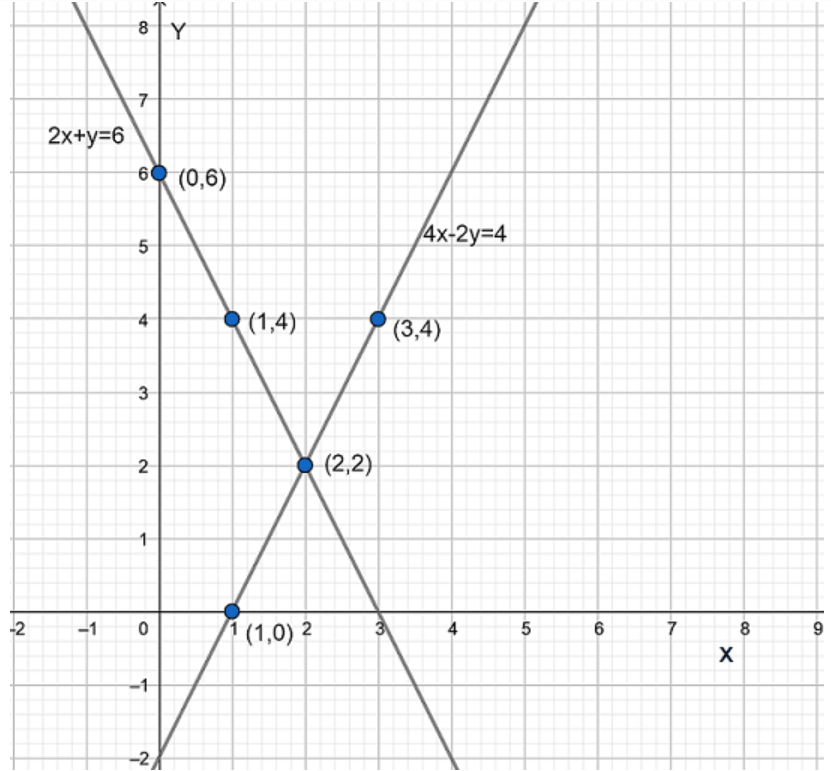
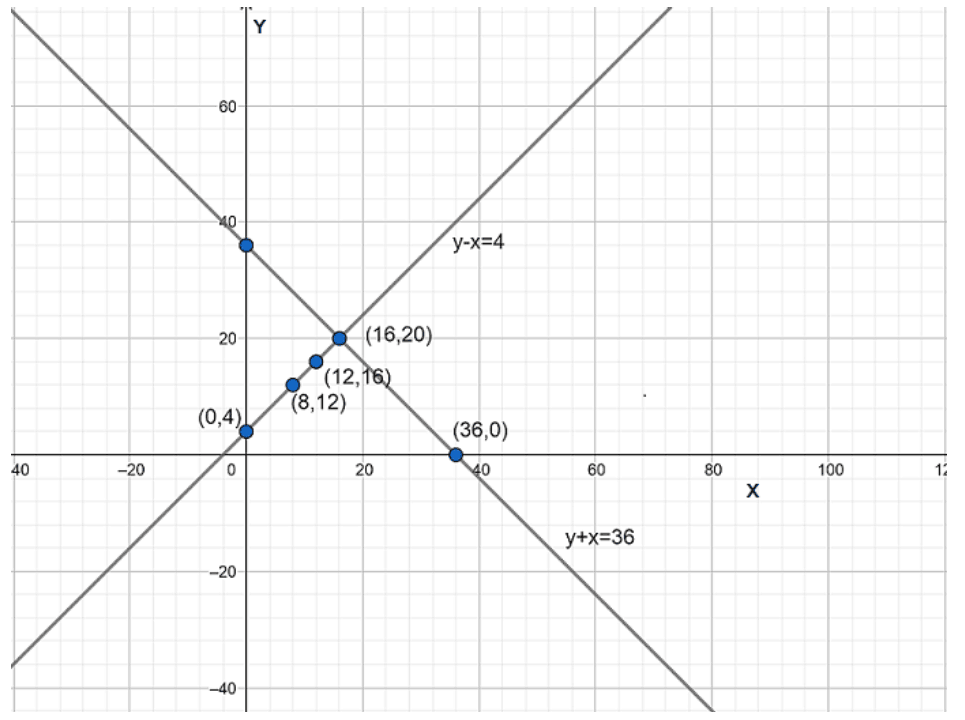
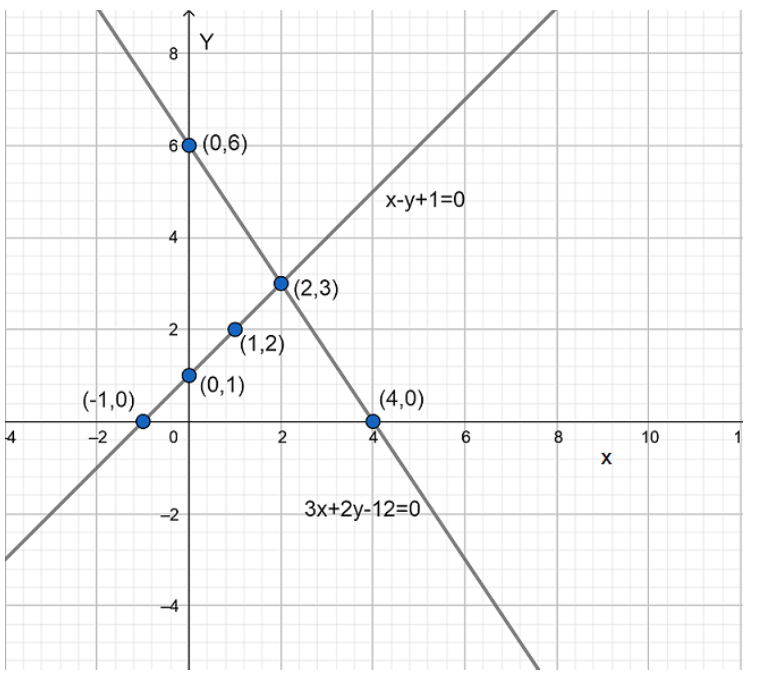
NCERT Solutions for Class 10 Maths Chapter 3 Exercise 3.1 uses the graphical method to solve a pair of linear equations. This method involves plotting both equations as straight lines on a coordinate plane and finding their point of intersection, which represents the unique solution, if it exists. If the lines are parallel, there is no solution, and if they coincide, there are infinitely many solutions.
2. How can you determine if a given pair of linear equations is consistent, inconsistent, or dependent in Class 10 Chapter 3 NCERT Solutions?
To check the nature of a pair of linear equations in two variables, compare the ratios of coefficients:
- If \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\), the lines intersect and the system is consistent with a unique solution.
- If \(\frac{a_1}{a_2} = \frac{b_1}{b_2} \neq \frac{c_1}{c_2}\), the lines are parallel and the system is inconsistent (no solution).
- If \(\frac{a_1}{a_2} = \frac{b_1}{b_2} = \frac{c_1}{c_2}\), the lines coincide and the system is dependent with infinitely many solutions.
3. What are the main steps to plot a pair of linear equations graphically as shown in NCERT Solutions for Class 10 Maths Chapter 3?
The main steps are:
- Express each equation in the form y = mx + c if possible.
- Choose at least two values for x, calculate corresponding y values to get coordinate points for each line.
- Plot these points on graph paper and draw the lines.
- The point where both lines meet is the solution.
4. Why does Class 10 Maths Chapter 3 Exercise 3.1 focus on the graphical method before algebraic methods?
The chapter introduces the graphical method first because it visually demonstrates how linear equations behave, helping students understand the concepts of intersection (unique solution), parallelism (no solution), and coincidence (infinite solutions). This foundational understanding supports success with later algebraic methods.
5. How do you identify the number of solutions for a pair of linear equations using NCERT Class 10 Maths Chapter 3 methodology?
Use these rules:
- Unique solution: The lines intersect at one point.
- Infinite solutions: The lines coincide (overlap completely).
- No solution: The lines are parallel and never meet.
6. What is considered a common mistake when plotting linear equations graphically in Class 10 linear equations chapters?
A frequent mistake is inaccurately calculating or plotting the points, which can lead to incorrect intersection points. It is critical to check calculations and use accurate graph scales to ensure the lines represent the equations exactly as per NCERT Solutions for Class 10 Maths Chapter 3 standards.
7. Can two different-looking linear equations represent the same line? Explain with context to Chapter 3, Exercise 3.1 NCERT Solutions.
Yes. Two equations can look different but represent the same line if one is a scalar multiple of the other. In such cases, their respective ratios of coefficients will be equal, indicating coincident lines and infinite solutions as explained in NCERT Solutions for Class 10 Maths Chapter 3.
8. What is the real-life application focus of the problems covered in NCERT Solutions for Class 10 Maths Chapter 3 Exercise 3.1?
Exercise 3.1 includes real-life scenarios requiring formation and solution of linear equations, such as calculating quantities, costs, and dimensions using two variables. The focus is on interpreting situations mathematically, translating them into equations, and finding practical solutions as per the CBSE syllabus.
9. According to NCERT Solutions Class 10 Maths Chapter 3, what is the significance of the coefficients in the equations?
The coefficients determine the slopes and intercepts of the lines when graphed. Comparing these allows students to predict intersection, parallelism, or coincidence of lines, which directly relates to the number of solutions for the pair of equations.
10. How should students verify their graphical solutions for Exercise 3.1 in Class 10 Maths NCERT Solutions?
After obtaining the intersection point from the graph, substitute the values of x and y back into both original equations. If both equations are satisfied, the graphical solution is verified as per NCERT Class 10 guidelines.
11. What are quick tips for solving problems in Class 10 Maths Chapter 3 Exercise 3.1 effectively, as recommended in NCERT Solutions?
- Plot points carefully and draw straight lines accurately.
- Use proper scaling on graph paper.
- Double-check calculations for points before plotting.
- Always verify intersection points by substitution.
- Understand coefficient ratios to quickly anticipate outcomes (unique/no/infinite solutions).
12. Why is understanding coincident and parallel lines crucial in Class 10 Maths Chapter 3?
Identifying coincident and parallel lines helps students instantly know whether equations have infinitely many solutions or none, reducing unnecessary calculations. Mastery of this concept is essential for higher-level problem-solving as required by CBSE 2025–26.
13. What if the point of intersection appears off-scale or in decimals when plotting Class 10 Maths Chapter 3 Exercise 3.1?
If the solution point is off-scale or involves decimals, extend the axes or use more precise point values for accurate graph plotting. Confirm the result by substituting values into the original equations for verification.
14. How does the graphical method in NCERT Solutions for Class 10 Maths Chapter 3 support error checking in algebraic solutions?
Plotting both equations allows students to visually confirm the solution obtained algebraically. If the graphical point does not satisfy both equations, an error in calculation or setup is likely. This reinforces accuracy, a key learning objective for Class 10 Maths NCERT Solutions.




















 Watch Video
Watch Video