




Introduction to Set Properties
A set contains elements or members that can be mathematical objects of any kind, including numbers, symbols, points in space, lines, other geometric shapes, variables, or even other sets. Set properties make it simple to execute many operations on sets. A set is a mathematical model for a collection of various things. Numerous properties, including commutative and associative qualities, are comparable to those of real numbers.
With the help of examples and frequently asked questions, let's learn more about the properties of the union of sets, the intersection of sets, and the complement of sets.
Properties of Sets
The traits of real numbers apply to sets as well. The three most important properties of sets are the associative property, the commutative property, and the other important property. The following are the formulas for the three sets of qualities, A, B, and C.
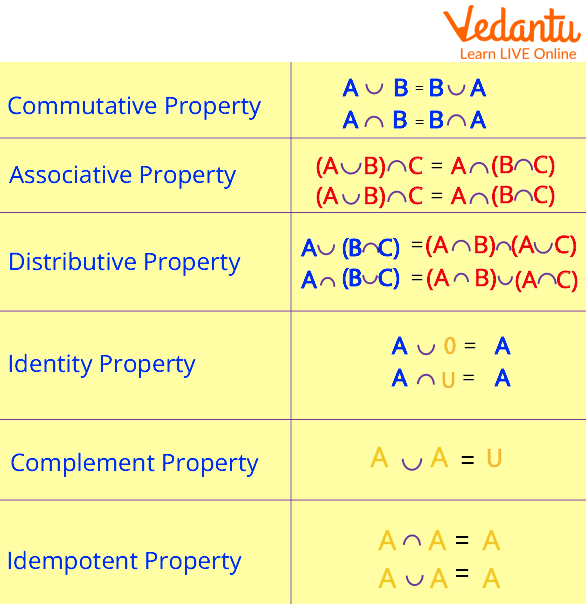
Properties of Sets
Using the above-mentioned set attributes, it is simple to conduct the various operations of the union of sets, the intersection of sets, and the complement of sets for the supplied sets.
Properties of Set Operations
A collection of well-defined items is referred to as a set in mathematics. A set's elements remain unchanged if the order in which they are written is changed. A set remains the same if one or more of its components are repeated. We shall discover the crucial characteristics of set operations in this essay.
1. Closure Property
2. Associative Property
3. Commutative Property
5. Identity Property
Conclusion
Sets have the same qualities as real numbers. Sets have the same associative property, commutative property, and other properties as numbers. The six essential properties of sets are commutative property, associative property, distributive property, identity property, complement property, and idempotent property.
Properties of Sets Problems
Example 1: Discover the complement of a set A and demonstrate that it complies with the double complement characteristic of sets. Given \[A = 1,2,4,5\] and \[\mu = 1,2,3,4,5,6,7,8,9,10\].
Solution: \[A = 1,2,4,5\]and \[\mu = 1,2,3,4,5,6,7,8,9,10\] are the given sets.
The objective is to demonstrate the double complement of sets \[\left( {A'} \right]' = A\] attribute.
\[\begin{array}{l}A = \left\{ {1,2,4,5,7} \right\}\\A' = \mu - A = \left\{ {3,6,8,9,10} \right\}\\\left( {A'} \right)' = \mu - A' = \left\{ {1,2,4,5,7} \right\}\end{array}\]
Since the set \[\left( {A'} \right)'\] above is identical to the supplied set A, we can conclude that\[\left( {A'} \right)' = A\].
As a result, the set in question adheres to the double complement feature of sets.
Example 2: Find the union of sets A and B, then demonstrate that it complies with the union of sets' commutative property. \[A = 1,2,3,4,5,6{\rm{ and }}B = 2,3,5,7,8,9\] are given.
Solution: The given sets are\[A = 1,2,3,4,5,6{\rm{ and }}B = 2,3,5,7,8,9\].
\[A \cup B = B \cup A\] is the commutative property of a union of sets.
\[A \cup B = \left\{ {1,2,3,4,5,6,7,8,9} \right\}\]
\[B \cup A = \left\{ {1,2,3,4,5,6,7,8,9} \right\}\] . We can see from the two sets above that\[A \cup B = B \cup A\].
As a result, the commutative property of the union of sets is observed in the two specified sets.
FAQs on Properties of Sets
1. What are the main properties of sets that students must understand for board exams?
The main properties of sets to focus on for the exams are the commutative, associative, distributive, identity, complement, and idempotent properties. Each property shows how sets behave under union, intersection, and complement operations, which are important for solving CBSE-based questions in the 2025–26 Maths syllabus.
2. Why is the commutative property important when working with sets in exam questions?
The commutative property helps in simplifying set operations by confirming that A ∪ B = B ∪ A and A ∩ B = B ∩ A. This means the order of sets does not affect the final result, which can make problem solving in exams more efficient and reduce calculation errors.
3. How does the associative property affect the grouping of sets during union and intersection?
The associative property allows you to group sets in any order during union or intersection operations: (A ∪ B) ∪ C = A ∪ (B ∪ C) and (A ∩ B) ∩ C = A ∩ (B ∩ C). This is useful in board exams when dealing with more than two sets, as it provides flexibility in calculation and logical steps.
4. How can one use the distributive property to simplify complex set expressions in board questions?
The distributive property enables you to expand or factor set expressions, for instance, A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C). Using this property helps break down complex expressions into simpler parts, which is a valuable technique for structured answers in CBSE Maths exams.
5. What is the significance of the identity property for sets in the CBSE syllabus?
The identity property states that a set combined with the empty set (∅) or the universal set (μ) doesn’t change its original composition:
- A ∪ ∅ = A
- A ∩ μ = A
6. Can you explain the double complement law with an example relevant to board exams?
The double complement law states that the complement of the complement of set A returns the original set: (A′)′ = A. For example, if A = {1,2,4,5} and the universal set μ = {1,2,3,4,5,6,7,8,9,10}, then:
- A' = μ – A = {3,6,7,8,9,10}
- (A′)′ = μ – A' = {1,2,4,5}
7. How do properties like idempotent and complement simplify solving set proof questions in exams?
The idempotent property (A ∪ A = A and A ∩ A = A) and the complement property (A ∪ A′ = μ, A ∩ A′ = ∅) reduce and clarify set expressions, which streamlines solutions for proofs and MCQs in competitive board examinations.
8. What type of set-based problems might appear as 5-mark questions in the 2025–26 board papers?
Typical 5-mark questions on sets often involve proving properties using precise reasoning, solving for unknowns in Venn diagrams, and demonstrating set laws like distributive or De Morgan's laws with examples as per the CBSE 2025–26 exam scheme.
9. What common mistakes should students avoid when applying set properties in exam solutions?
Some frequent errors include
- Confusing union (∪) and intersection (∩)
- Incorrectly finding complements without referencing the universal set
- Not applying associative/commutative properties when rearranging sets
- Overlooking the importance of brackets in set operations
10. How do board examiners check understanding of real-life applications of set properties?
Examiners may frame questions linking sets to real contexts, such as classroom groupings, survey data, or events, and ask students to use union, intersection, and other properties for logical conclusions. Applying set laws to solve these practical scenarios shows in-depth understanding and application skills expected in the CBSE Maths syllabus.











