
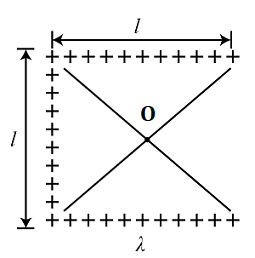
Three sides of a square of side \[l\] are occupied by positive charges of density $\lambda {\text{C}}/m$. The net electric field at the centre $O$ is:
(A) \[\dfrac{{\sqrt 2 {\text{k}}\lambda }}{l}\]
(B) $\dfrac{{2\sqrt 2 {\text{k}}\lambda }}{l}$
(C) $\dfrac{{2{\text{k}}\lambda }}{l}$
(D) $\dfrac{{{\text{k}}\lambda }}{l}$
Answer
148.5k+ views
Hint: Electric Field is the region produced around it by an electric charge whose influence is observed when in that region where the field exists, another charge is brought.
Formula Used: We will use the following formula to find out the solution of this problem:
\[E = \dfrac{{2\lambda }}{{x\sqrt {{l^2} + 4{x^2}} }}\]
Where
${\text{E}}$ is the net electric field
$\lambda $ is the electric charge density
$l$ is the length of the side of square
\[x\] is the distance from line charge
Complete Step-by-Step Solution:
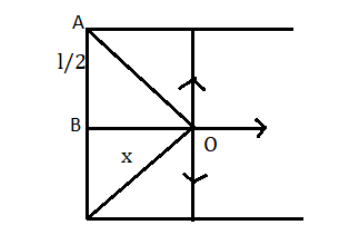
We have been given that the sides of the square are occupied by positive charges of density ${Q_{density}} = \lambda {\text{C}}/m$
The electric fields here are equal and opposite to each other due to the line charge of the top and bottom of the square. They cancel each other, and because of the line on the left side of the square, the net electric field at \[O\] is only the field.
In simpler words, we have
\[{E_{top}} = {E_{bottom}}\]
The charges on top and bottom are equal magnitude and opposite in polarity.
According to the question and the figure drawn above, we can observe that
\[x = \dfrac{l}{2}\]
Now we will put the values of \[x\] in the above formula, we get
\[E = \dfrac{{2\lambda }}{{k\dfrac{l}{2}\sqrt {{l^2} + \dfrac{{4{l^2}}}{4}} }}\]
We can rewrite this equation as
\[E = k\dfrac{{4\lambda }}{{\sqrt 2 l}}\]
Upon further simplifying, we get
\[E = \dfrac{{2\sqrt 2 k\lambda }}{l}\]
Therefore, the correct option is (B.)
Note: An electric field surrounds an electric charge and also exerts force at the same time on other charges in the field. It either attracts them or repels them. The electric field is defined mathematically as a vector field that connects the force per unit of charge exerted on an infinitesimal positive test charge to each point in space at that particular point. The volt per meter is the SI unit of electric field strength. Electric field strength is also denoted by Newtons per coulomb. Electric fields are generated by electrical charges, or by magnetic fields that vary in time.
Formula Used: We will use the following formula to find out the solution of this problem:
\[E = \dfrac{{2\lambda }}{{x\sqrt {{l^2} + 4{x^2}} }}\]
Where
${\text{E}}$ is the net electric field
$\lambda $ is the electric charge density
$l$ is the length of the side of square
\[x\] is the distance from line charge
Complete Step-by-Step Solution:

We have been given that the sides of the square are occupied by positive charges of density ${Q_{density}} = \lambda {\text{C}}/m$
The electric fields here are equal and opposite to each other due to the line charge of the top and bottom of the square. They cancel each other, and because of the line on the left side of the square, the net electric field at \[O\] is only the field.
In simpler words, we have
\[{E_{top}} = {E_{bottom}}\]
The charges on top and bottom are equal magnitude and opposite in polarity.
According to the question and the figure drawn above, we can observe that
\[x = \dfrac{l}{2}\]
Now we will put the values of \[x\] in the above formula, we get
\[E = \dfrac{{2\lambda }}{{k\dfrac{l}{2}\sqrt {{l^2} + \dfrac{{4{l^2}}}{4}} }}\]
We can rewrite this equation as
\[E = k\dfrac{{4\lambda }}{{\sqrt 2 l}}\]
Upon further simplifying, we get
\[E = \dfrac{{2\sqrt 2 k\lambda }}{l}\]
Therefore, the correct option is (B.)
Note: An electric field surrounds an electric charge and also exerts force at the same time on other charges in the field. It either attracts them or repels them. The electric field is defined mathematically as a vector field that connects the force per unit of charge exerted on an infinitesimal positive test charge to each point in space at that particular point. The volt per meter is the SI unit of electric field strength. Electric field strength is also denoted by Newtons per coulomb. Electric fields are generated by electrical charges, or by magnetic fields that vary in time.
Recently Updated Pages
Uniform Acceleration - Definition, Equation, Examples, and FAQs

Difference Between Mass and Weight

Young's Double Slit Experiment Step by Step Derivation

Wheatstone Bridge - Working Principle, Formula, Derivation, Application

JEE Main 2023 (January 29th Shift 1) Physics Question Paper with Answer Key

JEE Main 2021 July 20 Shift 2 Question Paper with Answer Key

Trending doubts
JEE Main 2025 Session 2: Application Form (Out), Exam Dates (Released), Eligibility, & More

JEE Main 2025: Derivation of Equation of Trajectory in Physics

Electric Field Due to Uniformly Charged Ring for JEE Main 2025 - Formula and Derivation

Degree of Dissociation and Its Formula With Solved Example for JEE

Electric field due to uniformly charged sphere class 12 physics JEE_Main

Electrical Field of Charged Spherical Shell - JEE

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

JEE Advanced 2025: Dates, Registration, Syllabus, Eligibility Criteria and More

JEE Advanced Weightage 2025 Chapter-Wise for Physics, Maths and Chemistry

A proton accelerated by a potential difference of 500 class 12 physics JEE_Main

Dual Nature of Radiation and Matter Class 12 Notes: CBSE Physics Chapter 11

Formula for number of images formed by two plane mirrors class 12 physics JEE_Main




