
A proton accelerated by a potential difference of 500 kV moves through a transverse magnetic field of \[0.51{\text{ }}T\] as shown in the figure. Then the angle $\theta $ through which the proton deviates from the initial direction of its motion is(approximately)

(A) $15^\circ $
(B) $30^\circ $
(C) $45^\circ $
(D) $60^\circ $
Answer
147.3k+ views
Hint: When the charged particle enters the charged region of the magnetic field, it will be deflected by the magnetic field and try to execute a circular motion. The radius of the circular motion depends on the velocity of the charged particle.
Formula used: In this solution, we will use the following formula:
-Radius of the circular motion of a charged particle in a magnetic field $r = \dfrac{{mv}}{{qB}}$ where $m$ is the mass of the charged particle, $v$ is its velocity, $q$ is the charge, and $B$ is the strength of the magnetic field.
Complete step by step answer:
When a charged particle moves in a magnetic field, it is deflected by the magnetic field. The particle is deflected such that the force of deflection will act perpendicular to its direction of velocity. The direction of the force can be determined by the left-hand rule. The charged particle will execute a circular motion, whose radius will be determined by
$r = \dfrac{{mv}}{{qB}}$
To calculate the radius of the particle, we need the velocity of the object.
We know that the charged particle, a proton accelerated by a potential difference of 500 kV. Hence the change in potential energy of the particle will be converted to kinetic energy as
$q\Delta V = \dfrac{1}{2}m{v^2}$
Substituting the value of $q = 1.6 \times {10^{19}}$, $\Delta V = 5 \times {10^5}\,V$, $m = 9.1 \times {10^{ - 31}}\,kg$ and $B = 0.51T$, we can get the velocity as
$v = 9.78 \times {10^6}\,m/s$
Then the radius of the particle will be determined from $r = \dfrac{{mv}}{{qB}}$ . Looking at the geometry of the charged particle as shown below,
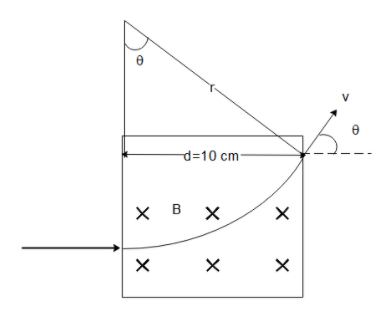
we can write $d = r\sin \theta $
Hence substituting the value of $r = \dfrac{{mv}}{{qB}}$, we get
$\sin \theta = \dfrac{{dqB}}{{mv}}$ which can be calculated as
$\sin \theta = 0.5$
Hence the angle formed by the charged particle will be
$\theta = 30^\circ $ which is an option (B).
Note: The force on the charged particle will be upwards as determined by the movement of the charged particle in a magnetic field facing inside the page. Hence the centre of the circular path will be in the vertically upward direction with the centre of the circle lying on the line containing the beginning of the magnetic field region.
Formula used: In this solution, we will use the following formula:
-Radius of the circular motion of a charged particle in a magnetic field $r = \dfrac{{mv}}{{qB}}$ where $m$ is the mass of the charged particle, $v$ is its velocity, $q$ is the charge, and $B$ is the strength of the magnetic field.
Complete step by step answer:
When a charged particle moves in a magnetic field, it is deflected by the magnetic field. The particle is deflected such that the force of deflection will act perpendicular to its direction of velocity. The direction of the force can be determined by the left-hand rule. The charged particle will execute a circular motion, whose radius will be determined by
$r = \dfrac{{mv}}{{qB}}$
To calculate the radius of the particle, we need the velocity of the object.
We know that the charged particle, a proton accelerated by a potential difference of 500 kV. Hence the change in potential energy of the particle will be converted to kinetic energy as
$q\Delta V = \dfrac{1}{2}m{v^2}$
Substituting the value of $q = 1.6 \times {10^{19}}$, $\Delta V = 5 \times {10^5}\,V$, $m = 9.1 \times {10^{ - 31}}\,kg$ and $B = 0.51T$, we can get the velocity as
$v = 9.78 \times {10^6}\,m/s$
Then the radius of the particle will be determined from $r = \dfrac{{mv}}{{qB}}$ . Looking at the geometry of the charged particle as shown below,

we can write $d = r\sin \theta $
Hence substituting the value of $r = \dfrac{{mv}}{{qB}}$, we get
$\sin \theta = \dfrac{{dqB}}{{mv}}$ which can be calculated as
$\sin \theta = 0.5$
Hence the angle formed by the charged particle will be
$\theta = 30^\circ $ which is an option (B).
Note: The force on the charged particle will be upwards as determined by the movement of the charged particle in a magnetic field facing inside the page. Hence the centre of the circular path will be in the vertically upward direction with the centre of the circle lying on the line containing the beginning of the magnetic field region.
Recently Updated Pages
JEE Main 2023 (January 29th Shift 1) Physics Question Paper with Answer Key

JEE Main 2021 July 20 Shift 2 Question Paper with Answer Key

JEE Main 2023 January 30 Shift 2 Question Paper with Answer Key

JEE Main 2022 (June 24th Shift 1) Physics Question Paper with Answer Key

Equivalent Capacitance - Important Concepts and Tips for JEE

JEE Main 2023 (April 6th Shift 1) Physics Question Paper with Answer Key

Trending doubts
JEE Main 2025 Session 2: Application Form (Out), Exam Dates (Released), Eligibility, & More

JEE Main Exam Marking Scheme: Detailed Breakdown of Marks and Negative Marking

JEE Main 2025: Derivation of Equation of Trajectory in Physics

Electric Field Due to Uniformly Charged Ring for JEE Main 2025 - Formula and Derivation

JEE Main Participating Colleges 2024 - A Complete List of Top Colleges

Degree of Dissociation and Its Formula With Solved Example for JEE

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

JEE Advanced 2025: Dates, Registration, Syllabus, Eligibility Criteria and More

JEE Advanced Weightage 2025 Chapter-Wise for Physics, Maths and Chemistry

Electric field due to uniformly charged sphere class 12 physics JEE_Main

Learn About Angle Of Deviation In Prism: JEE Main Physics 2025

Electrical Field of Charged Spherical Shell - JEE




