Learn How Fluid Velocity Affects Pressure: Class 12 Physics Experiment

Introduction

The relation between the pressure energy, kinetic energy, and potential energy of a fluid can be described using Bernoulli's theorem. It can be explained using the apparatus using a venturi meter. It is a tool used to determine the flow of a fluid. Here, a converging pipe section is employed to increase flow velocity and a corresponding pressure drop, from which Bernoulli's equation is used to determine the fluid's flow rate.

A fluid accelerates in the convergent section of a venturi meter before decelerating in the divergent region. A manometer measures the pressure difference between the neck and an upstream portion. Therefore, the volumetric flow rate can be calculated using that differential pressure, Bernoulli's, and continuity equation.

Table of Contents

1. Aim

2. Apparatus Required

3. Theory 

4. Procedure

5. Observations 

6. Result

7. Precautions

8. Lab Manual Questions 

9. Viva Questions 

10. Practical Based Questions 

11. Conclusion

12. FAQs

Aim

To observe the decrease in pressure with an increase in the velocity of a fluid.

Apparatus Required

1. Venturimeter

2. Two Narrow Tubes

3. Vernier Calliper

4. Scale

5. Water

Theory

Based on the principle of conservation of energy, Bernoulli's theorem states that “the total amount of energy present in a fluid during a steady flow is constant at all sites when viscous forces are absent.” This means that the total of all forms of energy- mechanical, internal, etc., remains constant. Therefore, for a fluid flowing horizontally (without change in its height from the ground), we have

$P \ + \ \dfrac{1}{2} \rho v^2 \ = \ constant$

Here, $P \ = \ pressure \ of \ fluid$

$\rho \ = \ density \ of \ fluid$

$v \ = \ velocity \ of \ fluid$

Also, $Av \ = \ constant$

Where $A \ = \ area \ of \ cross-section \ of \ pipe$

And, $P \ = \ \rho gh$

$g \ = \ acceleration \ due \ to \ gravity$

$h \ = \ height$

Therefore when the pressure decreases the velocity increases. The same is valid for the reverse. In a narrow tube, the flow is at a higher velocity than in a broad tube.

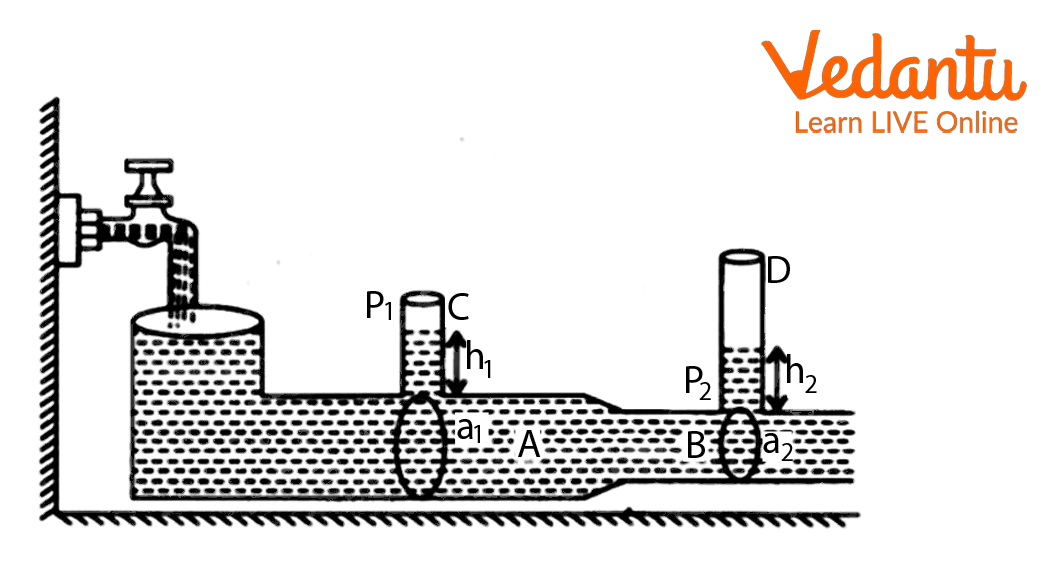
Apparatus for the experiment

Procedure

1. Measure the two diameters of the venturi meter.

2. Connect pipes $C$ and $D$ to the apertures given in the venturimeter so that they remain vertical and parallel.

3. Fill the venturimeter with water from a tap gradually, so the flow remains steady at all points and at all times.

4. Using a meter scale, measure the heights $h_1$ and $h_2$ in the pipes $C$ and $D$ respectively. 

5. Using the heights thus measured, calculate the pressure in the two pipes.

6. Increase the rate of flow of water for four more readings of the heights measured in step 5.

Observation

Observation Table

1. Least count of meter scale:

2. Mean diameter of broad pipe:

Area $a_1$ of broad pipe: $\pi r^2_1 \ = \ \pi \dfrac{d^2_1}{4}$
Mean diameter of narrow pipe:
Area $a_2$ of narrow pipe: $\pi r^2_2 \ = \ \pi \dfrac{d^2_2}{4}$

3. Velocity of broad pipe $= \ v_1$
   Velocity of narrow pipe $= \ v_2$
   From equation of continuity,
   $a_1v_1 \ = \ a_2v_2$

Or, $\dfrac{a_1}{a_2} \ = \ \dfrac{v_2}{v_1}$

4. Density of water: $1 \ g/cm^3$

5. Acceleration due to gravity $(g): \ 980 \ cm/s^2$

Result

Ratio of velocities of water in venturimeter pipes using $\dfrac{v_1}{v_2} \ = \ \dfrac{\pi \dfrac{d^2_2}{4}}{\pi \dfrac{d^2_2}{4}}$ :

Pressure of water in pipes $C$ and $D$ using $P \ = \ \rho gh$ :

Precautions

1. Steady flow should be maintained throughout.

2. There should be no leakage between connections.

3. The venturimeter apparatus should be horizontal.

4. The pipes $C$ and $D$ attached must be vertical and parallel.

Lab Manual Questions

1. Define briefly each of the terms used in Bernoulli’s theorem.

Ans: Bernoulli's theorem states, "A drop in fluid pressure is linked to an increase in fluid velocity if the fluid is flowing horizontally and there is no change in gravitational potential energy.” Mathematically, for a point, it is expressed as $P \ + \dfrac{1}{2} \rho v^2 \ + \ \rho gh \ = \ constant$

Here, $P$ represents pressure of fluid at a point, $\rho$ represents liquid density, $v$ represents fluid velocity, $g$ represents acceleration due to gravity and $h$ represents height from reference point.

2. What is the difference between steady and turbulent flow?

Ans: A fluid motion is said to be steady if its velocity at a given position is independent of time, although the fluid's velocity may vary at various points in space. Turbulent flow is defined as a flow in which the liquid particle behaviour is unpredictable or lacks any discernible pattern.

3. If water flows through a tube of non-uniform cross-section area, what is the effect on the speed and pressure of water once it reaches the narrowest portion?

Ans: We know that $cross-section \ area \times velocity \ = \ constant$

Therefore, cross-section area and speed are inversely proportional. As the cross-sectional area decreases, the speed increases.

Now, using Bernoulli’s equation, $P \ + \dfrac{1}{2} \rho v^2 \ + \ \rho gh \ = \ constant$ (assuming h constant, and thus neglecting $\rho gh$)

where $P$ represents the pressure of the fluid at a point, $\rho$ represents liquid density, $v$ represents fluid velocity, $g$ represents acceleration due to gravity and $h$ represents height from a reference point.

As speed increases, pressure must decrease.

4. Explain on which law Bernoulli's theorem is based.

Ans: The energy conservation law serves as the foundation for Bernoulli's principle. It compares the total energy of a liquid at various sites flowing under constant pressure differences (including pressure energy, potential energy, and kinetic energy).

Viva Questions

1. State Bernoulli's theorem and its equation.

Ans: Bernoulli's theorem states, "A drop in fluid pressure is linked to an increase in fluid velocity if the fluid flows horizontally and there is no change in gravitational potential energy.” It compares the total energy of a liquid at various sites flowing under constant pressure differences (including pressure energy, potential energy, and kinetic energy). Mathematically, for a point, it is expressed as $P \ + \dfrac{1}{2} \rho v^2 \ + \ \rho gh \ = \ constant$

Here, $P$ represents the pressure of the fluid at a point, $\rho$ represents liquid density, $v$ represents fluid velocity, $g$ represents acceleration due to gravity, and $h$ represents height from a reference point.

2. Is Bernoulli’s theorem only valid for liquids? Why or why not?

Ans: Bernoulli’s theorem is valid for all fluids- liquids and gases. This is because it compares the total energy of a flowing liquid at various sites flowing under constant pressure differences (including pressure energy, potential energy, and kinetic energy). These are all exhibited by fluids.

3. What is Reynolds number, and what does it state?

Ans: Reynolds number, a dimensionless quantity, is used to categorise the flow pattern through a laminar or turbulent pipe.

Laminar flow is defined as having a Reynolds number of less than 2000, and turbulent flow as having a Reynolds number of more than 4000.

4. Why is Bernoulli’s theorem valid only for non-viscous fluids?

Ans: Bernoulli's theorem is based on the law of conservation of energy. The equation only applies to non-viscous fluids since viscous energy losses, which occur in fluids with high viscosity and are not conserved, would require an additional energy source to prevent deceleration, such as increased pressure.

5. State the equation of continuity. Which law is it based on?

Ans: The continuity equation demonstrates the law of mass conservation in fluid dynamics. The density will remain constant for steady flow only if the fluid is incompressible. It relates density $\rho$, cross-section area $A$ and speed $v$ of fluid as $\rho Av \ = \ constant$

6. Mention the possible sources of error in the experiment.

Ans: Some sources of error are as follows:

1. The flow might not be steady.

2. Fluid used might not be ideal.

3. Apparatus might not be perfectly horizontal.

7. Define viscosity.

Ans: A fluid's resistance to deformation at a specific rate is measured by its viscosity. It is equivalent to the colloquial term for "thickness" in liquids.

8. Is Bernoulli’s theorem valid for compressible liquids? Why or why not?

Ans: Bernoulli’s theorem is valid only for non-viscous incompressible fluids. This is because, for incompressible fluids, the density is variable. However, Bernoulli’s theorem involves the use of the continuity equation wherein the density change will have to be accounted for.

9. Why is the Magnus effect observed?

Ans: The Magnus effect occurs on rotating spherical or cylindrical objects. We can see the result of this impact when the moving, spinning object deviates from its intended path. Due to momentum conservation, the object's rotation changes the airflow around the body, which results in the Magnus effect.

10. Which factors affect the velocity of efflux from the hole located at the bottom of a tank filled with a liquid?

Ans: The velocity of efflux depends on the density of fluid, the acceleration due to gravity and height of water in the container. It is independent of the size of the aperture. 

Practical Based Questions

1. Bernoulli’s theorem can be expressed by which among the following equations?

1. $ P \ + \ \dfrac{1}{2} \rho v \ + \ \rho gh \ = \ constant$

2. $ P \rho \ + \ \dfrac{1}{2} \rho v^2 \ + \ \rho gh \ = \ constant$

3. $ P \ + \ \dfrac{1}{2} \rho v^2 \ + \ \rho gh \ = \ constant$

4. $ \dfrac{P}{\rho} \ + \ \dfrac{1}{2} \rho v^2 \ + \ \rho gh \ = \ constant$

Answer: (c)

2. Which phenomenon explains the blowing off of a roof during a storm?

1. Pascal’s principle

2. Bernoulli’s theorem

3. Stokes law

4. Archimedes principle

Answer: (b)

3. The correct statement(s) among the following is/are:

1. Bernoulli’s theorem holds true when the flow is steady

2. Equation of continuity is $A_1 v_1 \ = \ A_2 v_2$

3. Poise is the CGS unit of viscosity

4. All of the above

Answer: (d)

4. Which among the following is based on the law of conservation of energy?

1. Bernoulli’s theorem

2. Equation of continuity

3. Stroke’s law

4. None of these

Answer: (a)

5. A plane in level flight with a wingspan of $20 \ m^2$. It is moving with a constant speed. Determine the plane of the mass if the speed of air over the lower and upper wing are $198 \ km/hr$ and $270 \ km/hr$ respectively.

1. $5306.1 \ kg$

2. $26000 \ kg$

3. $52000 \ kg$

4. $6432.1 \ kg$

Answer: (a)

6. A spinning ball is thrown in the blowing air. The path of the ball becomes curved because:

1. Compton effect

2. Seebeck effect

3. Magnus effect

4. Doppler effect

Answer: (c)

7. If water flows through the broader portion of pipe of non-uniform cross section area at the speed of $50 \ cm/s$ and the pressure difference is maintained at $1.6 \ cm$ of mercury, find the speed of water in the narrow portion.

1. $ \sqrt{4.09}$

2. $\sqrt{2.88}$

3. $ \sqrt{2.38}$

4. $ \sqrt{4.51}$

Answer: (d)

8. The damage to eardrum in deeper areas of the sea is caused due to:

1. Lack of oxygen

2. High water pressure

3. High atmospheric pressure

4. All of the above

Answer: b

9. What happens when the pipe is constricted for fluid flowing through a horizontal pipe?

1. Velocity increases and pressure decreases

2. Velocity decreases and pressure increases

3. Both velocity and pressure decrease

4. Both velocity and pressure increase

Answer: (a)

10. The restriction on application of Bernoulli’s theorem on fluids is

1. Should have high viscosity

2. Be of unit density

3. Be at high atmospheric pressure

4. Must be incompressible

Answer: (d)

Summary

Bernoulli’s theorem is used to explain the decrease in pressure with an increase in velocity, or vice-versa. It is based on the principle of energy conservation, which states that total energy remains constant although it changes forms. The theorem includes all forms of energy in its equation- $ P \ + \ \dfrac{1}{2} \rho v^2 \ + \ \rho gh \ = \ constant$, using $P$ for pressure, $\rho$ for density of the fluid, $v$ for velocity, $g$ for acceleration due to gravity and $h$ for height. The change in height can be calculated by changing the fluid flow through a venturimeter. Adding the known quantities, pressure can be calculated, and it can be proved that pressure and velocity are inversely related.