Determinants Class 12 Notes: CBSE Maths Chapter 4

Recollecting Concepts

When a system of algebraic equations is given to us as:

${{a}_{1}}x+{{b}_{1}}y={{c}_{1}}$

${{a}_{2}}x+{{b}_{2}}y={{c}_{2}}$

Then we can express them in the form of matrices as:

$\left[ \begin{matrix} {{a}_{1}} & {{b}_{1}}  \\ {{a}_{2}} & {{b}_{2}}  \\ \end{matrix} \right]\left[ \begin{matrix} x  \\ y  \\ \end{matrix} \right]=\left[ \begin{matrix} {{c}_{1}}  \\ {{c}_{2}}  \\ \end{matrix} \right]$

To get the solution of a system of linear equations, we find all the values of the variables satisfying all the linear equations in the system.

Definition of Determinants

• We can define the determinant of a matrix as a scalar value that can be calculated from the elements of a square matrix.

• The scalar value for a square matrix  $\left[ \begin{matrix} {{a}_{1}} & {{b}_{1}}  \\ {{a}_{2}} & {{b}_{2}}  \\ \end{matrix} \right]$ is given by ${{a}_{1}}{{b}_{2}}-{{a}_{2}}{{b}_{1}}$.

• It is represented as $\left| A \right|$ or det $\left( A \right)$ or $\Delta $.

• For a matrix  $\left[ \begin{matrix} {{a}_{1}} & {{b}_{1}}  \\ {{a}_{2}} & {{b}_{2}}  \\ \end{matrix} \right]$, the determinant is written as $\left| \begin{matrix} {{a}_{1}} & {{b}_{1}}  \\ {{a}_{2}} & {{b}_{2}}  \\ \end{matrix} \right|$.

• Square matrices are those matrices that have the same number of rows and columns. Only such matrices have determinants.

Types of Determinants

1. First Order Determinant – It is the determinant of a matrix of order one. The element of the matrix will be the determinant value. 

For example,

$\left[ 2 \right]\Rightarrow \left| 2 \right|\Rightarrow 2$ 

2. Second Order Determinant - It is the determinant of a matrix of order two.

If $\left[ \begin{matrix} {{a}_{1}} & {{b}_{1}}  \\ {{a}_{2}} & {{b}_{2}}  \\ \end{matrix} \right]$, then $\left| \begin{matrix} {{a}_{1}} & {{b}_{1}}  \\ {{a}_{2}} & {{b}_{2}}  \\ \end{matrix} \right|={{a}_{1}}{{b}_{2}}-{{a}_{2}}{{b}_{1}}$.

For example,

$\left[ \begin{matrix} 1 & 3  \\ 5 & 3  \\ \end{matrix} \right]\Rightarrow \left| \begin{matrix} 1 & 3  \\ 5 & 3  \\ \end{matrix} \right|$ 

$\Rightarrow \left( 1\times 3 \right)-\left( 3\times 5 \right)\Rightarrow 3-15\Rightarrow -12$

3. Third Order Determinant - It is the determinant of a matrix of order three.

Let us consider $\left[ \begin{matrix} {{a}_{1}} & {{b}_{1}} & {{c}_{1}}  \\ {{a}_{2}} & {{b}_{2}} & {{c}_{2}}  \\ {{a}_{3}} & {{b}_{3}} & {{c}_{3}}  \\ \end{matrix} \right]$. 

We have six ways to write the determinant, i.e. three ways to expand along rows and three ways to expand along columns.

Let us consider the expansion along the first row, which is the most common method.

So, first we consider the first element, ${{a}_{11}}$ and delete the row \[1\] and column $1$. We end up with a second order matrix and so we apply the determinant for this and multiply with ${{a}_{11}}$ and also \[{{\left( -1 \right)}^{sum\text{ }of\text{ }coefficients\text{ }of\text{ }{{a}_{11}}}}\Rightarrow {{\left( -1 \right)}^{1+1}}\], here sum of coefficients indicates the sum $i+j$ for element ${{a}_{ij}}$.

${{\left( -1 \right)}^{2}}.{{a}_{1}}.\left( {{b}_{2}}{{c}_{3}}-{{b}_{3}}{{c}_{2}} \right)$ 

Then we move onto element ${{a}_{12}}$ and delete the row \[1\] and column $2$. Again, We end up with a second order matrix and so we apply the determinant for this and multiply with \[{{a}_{12}}\] and also \[{{\left( -1 \right)}^{sum\text{ }of\text{ }coefficients\text{ }of\text{ }{{a}_{12}}}}\Rightarrow {{\left( -1 \right)}^{1+2}}\].

${{\left( -1 \right)}^{3}}.{{b}_{1}}.\left( {{a}_{2}}{{c}_{3}}-{{a}_{3}}{{c}_{2}} \right)$

At last, we move onto element ${{a}_{13}}$ and delete the row \[1\] and column $3$.

Again, We end up with a second order matrix and so we apply the determinant for this and multiply with ${{a}_{13}}$ and also \[{{\left( -1 \right)}^{sum\text{ }of\text{ }coefficients\text{ }of\text{ }{{a}_{13}}}}\Rightarrow {{\left( -1 \right)}^{1+3}}\].

${{\left( -1 \right)}^{4}}.{{c}_{1}}.\left( {{a}_{2}}{{b}_{3}}-{{a}_{3}}{{b}_{2}} \right)$

Now, we add them up to get the determinant of matrix 

$\left[ \begin{matrix} {{a}_{1}} & {{b}_{1}} & {{c}_{1}}  \\ {{a}_{2}} & {{b}_{2}} & {{c}_{2}}  \\ {{a}_{3}} & {{b}_{3}} & {{c}_{3}}  \\ \end{matrix} \right]$ as 

${{a}_{1}}\left( {{b}_{2}}{{c}_{3}}-{{b}_{3}}{{c}_{2}} \right)-{{b}_{1}}\left({{a}_{2}}{{c}_{3}}-{{a}_{3}}{{c}_{2}} \right)+{{c}_{1}}\left({{a}_{2}}{{b}_{3}}-{{a}_{3}}{{b}_{2}} \right)$.

In the same manner, we can expand along other rows and columns. We will get the same value of determinant irrespective of the kind of expansion we opt for.

A tip to keep in mind while choosing the expansion method would be to go for the row or column containing the maximum number of zeroes. If zeroes are not present, then one. This will make calculations easier.

Another interesting point to keep in mind is that if we have two square matrices $A$ and $B$ of order $n$ and $A=kB$, then $\left| A \right|={{k}^{n}}\left| B \right|$, where $n=1,2,3,....$.

Area of a Triangle

• Consider a triangle with vertices as $\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right)$ and $\left( {{x}_{3}},{{y}_{3}} \right)$. We know that the area of the triangle can be found as $A=\dfrac{1}{2}\left[ {{x}_{1}}\left( {{y}_{2}}-{{y}_{3}} \right)+{{x}_{2}}\left( {{y}_{3}}-{{y}_{1}} \right)+{{x}_{3}}\left( {{y}_{1}}-{{y}_{2}} \right) \right]$.

• We can represent the same using determinants as $\Delta$ =$\dfrac{1}{2}\left| \begin{matrix} {{x}_{1}} & {{y}_{1}} & 1  \\ {{x}_{2}} & {{y}_{2}} & 1  \\ {{x}_{3}} & {{y}_{3}} & 1  \\ \end{matrix} \right|$.

• We always take the absolute value of the determinant while computing the area as it is a positive quantity.

• We use both positive and negative values of the determinant in case the area is given.

• We know that three collinear points cannot form a triangle and hence we can say that the area of the triangle formed by three collinear points is zero.

Minors

• If we delete the ${{i}^{th}}$ row and \[{{j}^{th}}\] column of a determinant in which the element ${{a}_{ij}}$ lies, then we get the minor of that element.

• Minor is represented as \[{{M}_{ij}}\].

• Minor of an element of a determinant of order \[n\left( n\ge 2 \right)\] is a determinant of order \[n1\].

• If we have to find \[{{M}_{21}}\] of determinant \[\left| \begin{matrix} 1 & -4 & 0  \\ 2 & 5 & 3  \\ -1 & 2 & 1  \\ \end{matrix} \right|\], then we get it as \[{{M}_{21}}=\left| \begin{matrix} -4 & 0  \\ 2 & 1  \\ \end{matrix} \right|\Rightarrow {{M}_{21}}=-4\].

Cofactors

• We denote the cofactor of an element \[{{a}_{ij}}\] as ${{A}_{ij}}$.

• Multiplying the minor of an element with a factor \[{{\left( 1 \right)}^{i+j}}\] gives the cofactor.

• It can be defined as \[{{A}_{ij}}=\text{ }{{\left( 1 \right)}^{i+j}}{{M}_{ij}}\], where \[{{M}_{ij}}\] is minor of \[{{a}_{ij}}\].

• When the elements of a row/column are multiplied with the cofactors of any other row/column, then their sum is zero.

• If we have to find \[{{A}_{11}}\] of determinant \[\left| \begin{matrix} 1 & -4 & 0  \\ 2 & 5 & 3  \\ -1 & 2 & 1  \\ \end{matrix} \right|\], then we get it as \[{{A}_{11}}={{\left( -1 \right)}^{1+1}}\left| \begin{matrix} 5 & 3  \\ 2 & 1  \\ \end{matrix} \right|\Rightarrow {{A}_{11}}=1.\left( 5-6 \right)\Rightarrow {{A}_{11}}=-1\].

Adjoint of a Matrix

• The matrix obtained after taking the transpose of the matrix of cofactors of the given matrix is called the adjoint of that matrix.

• For example, if we have the cofactor matrix as \[\left[\begin{matrix} a & b & c  \\ d & e & f  \\ g & h & i  \\ \end{matrix} \right]\], then the adjoint would be $\left[ \begin{matrix} a & d & g  \\ b & e & h  \\ c & f & i  \\ \end{matrix} \right]$.

• For a square matrix of order two, we can use the following shortcut:

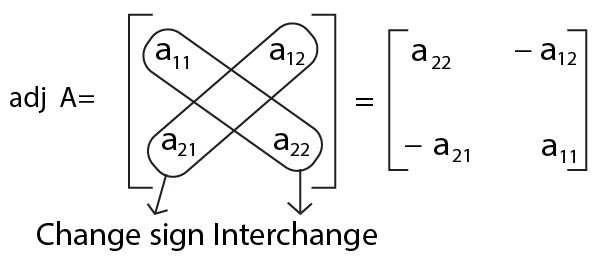
• Theorem 1 - If $A$ be any given square matrix of order $n$, then \[A\left( adj\text{ }A \right)=\left( adj\text{ }A \right)A=\left| A \right|I\], where $I$ is the identity matrix of order $n$.

If we have a matrix $\left[ \begin{matrix} a & b  \\ c & d  \\ \end{matrix} \right]$ and its adjoint as $\left[ \begin{matrix} e & f  \\ g & h  \\ \end{matrix} \right]$, then we can say that the sum of product of elements of a row/column with corresponding cofactors is equal to \[\left| A \right|\] and otherwise zero. So, we can write

$A\left( adj\text{ }A \right)=\left[ \begin{matrix} \left| A \right| & 0  \\ 0 & \left| A \right|  \\ \end{matrix} \right]=\left| A \right|I$

• Singular Matrices – If the determinant of a square matrix is zero, then it is said to be a singular matrix.

• Non-Singular Matrices – If the determinant of a square matrix is a non-zero value, then it is said to be a non-singular matrix.

• Theorem 2 - If $A$ and $B$ are nonsingular matrices of the same order, then $AB$ and $BA$ are also non-singular matrices of the same order.

• Theorem 3 - The determinant of the product of matrices is equal to the product of their respective determinants. It can be written as \[AB=\left| A \right|\left| B \right|\], where $A$ and $B$ are square matrices of the same order.

This can be verified as shown below:

From Theorem 1, we have $A\left( adj\text{ }A \right)=\left[ \begin{matrix} \left| A \right| & 0  \\ 0 & \left| A \right|  \\ \end{matrix} \right]$. 

Now taking the determinant value of matrices on both sides,

$\left| A\left( adj\text{ }A \right) \right|=\left| \begin{matrix} \left| A \right| & 0  \\ 0 & \left| A \right|  \\ \end{matrix} \right|$

$\left| A \right|\left| \left( adj\text{ }A \right) \right|={{\left| A \right|}^{2}}\left| \begin{matrix} 1 & 0  \\ 0 & 1  \\ \end{matrix} \right|$

$\left| A \right|\left| \left( adj\text{ }A \right) \right|={{\left| A \right|}^{2}}I$

$\left| \left( adj\text{ }A \right) \right|={{\left| A \right|}^{1}}$

Hence verified. This leads us to the general conclusion that if $A$ is a square matrix of order $n$, then $\left| \left( adj\text{ }A \right) \right|={{\left| A \right|}^{n-1}}$.

• Theorem 4 - A square matrix is invertible if and only if it is a non-singular matrix.

So, for a non-singular matrix $A$, we can write the inverse of the matrix as ${{A}^{-1}}=\dfrac{1}{\left| A \right|}\left( adj\text{ }A \right)$.

Looking into the proof,

Let $A$ be an invertible matrix of order $n$. Let $I$ be the identity matrix of order $n$. Then, there exists a square matrix $B$ of order $n$ such that \[AB=BA=I\].

So, we have \[AB=I\]. We can write \[\left| AB \right|=I\]. Since \[\left| I \right|=1,\left| AB \right|=\left| A \right|\left| B \right|\], it can be written as \[\left| A \right|\left| B \right|=1\].

This gives \[\left| A \right|\ne 0\] and hence $A$ is non-singular.

Conversely, if we let $A$ as a non-singular matrix, then \[\left| A \right|\ne 0\].

From Theorem 1, \[A\left( adj\text{ }A \right)=\left( adj\text{ }A \right)A=\left| A \right|I\]. Rearranging terms,

\[A\left[ \dfrac{1}{\left| A \right|}\left( adj\text{ }A \right) \right]=\left[ \left( adj\text{ }A \right)\dfrac{1}{\left| A \right|} \right]A=I\]

It is the same as $AB=BA=I$.

So, here $B=\dfrac{1}{\left| A \right|}\left( adj\text{ }A \right)$, which is the inverse of matrix $A$.

Applications of Determinants and Matrices

• They can be used for solving systems of linear equations in two or three variables. They can also be used for checking the consistency of a system of linear equations.

• Consistent system is a system of equations whose solution (one or more) exists.

• Inconsistent system is a system of equations whose solution does not exist.

• We can say that the determinant is a number that determines the uniqueness of the solution of a system of linear equations.

Solution of a System of Linear Equations Using Inverse of Matrix

Let us consider system of equations with three variables as

${{a}_{1}}x+{{b}_{1}}y+{{c}_{1}}z={{d}_{1}}$

${{a}_{2}}x+{{b}_{2}}y+{{c}_{2}}z={{d}_{2}}$

${{a}_{3}}x+{{b}_{3}}y+{{c}_{3}}z={{d}_{3}}$

Writing it in matrix form, we have

$\left[ \begin{matrix} {{a}_{1}} & {{b}_{1}} & {{c}_{1}}  \\ {{a}_{2}} & {{b}_{2}} & {{c}_{2}}  \\ {{a}_{3}} & {{b}_{3}} & {{c}_{3}}  \\ \end{matrix} \right]\left[ \begin{matrix} x  \\ y  \\ z  \\ \end{matrix} \right]=\left[ \begin{matrix} {{d}_{1}}  \\ {{d}_{2}}  \\ {{d}_{3}}  \\ \end{matrix} \right]$

This can be expressed as $AX=B$.

• Now, we look at two cases:

Case 1: If $A$ is a non-singular matrix, then its inverse exists.

From $AX=B$, we premultiply by ${{A}^{-1}}$,

${{A}^{-1}}\left( AX \right)={{A}^{-1}}B$

Using associative property,

$\left( {{A}^{-1}}A \right)X={{A}^{-1}}B$

$IX={{A}^{-1}}B$

$X={{A}^{-1}}B$

The above matrix equation provides a unique solution for the system of equations as we know that the inverse of a matrix is unique. We call this method as Matrix Method.

Case 2: If $A$ is a singular matrix, then \[\left| A \right|=0\].

For this case, first we calculate \[\left( adj\text{ }A \right)B\].

If \[\left( adj\text{ }A \right)B\] is a non-zero matrix, then the solution does not exist and the system of equations is called inconsistent.

If \[\left( adj\text{ }A \right)B\] is a zero matrix, then the system of equations may be either consistent (with infinitely many solutions) or inconsistent (with no solution).

Important Formulas of Class 12 Chapter 4 You Shouldn’t Miss!

\[\text{If } A = \begin{pmatrix} a & b \\ c & d \end{pmatrix}, \text{ then } \text{det}(A) = ad - bc\]

Determinant of a 3x3 Matrix

\[\text{If } A = \begin{pmatrix} a & b & c \\ d & e & f \\ g & h & i \end{pmatrix}, \text{det}(A) = a(ei - fh) - b(di - fg) + c(dh - eg)\]

$\text{Determinant of a Transpose:} \quad \det\left( A^T \right) = \det\left( A \right)$

Cofactor and Minor

Minor of an Element: The minor Mij of an element aij is the determinant of the submatrix formed by deleting the ith row and jth column of the original matrix. 

Cofactor of an Element:The cofactor Cij is given by  Cij = -1i+j Mij

Adjoint of a Matrix

Adj(A) = Transpose of the cofactor matrix of A

Inverse of a Matrix Using Determinants

\[A^{-1} = \frac{1}{\text{det}(A)} \times \text{Adj}(A), \text{ provided } \text{det}(A) \neq 0\]

Determinant of a Triangular Matrix

For a triangular matrix (upper or lower), the determinant is the product of the diagonal elements.

Area of a Triangle Using Determinants

\[\text{Area} = \frac{1}{2} \times \left| \begin{pmatrix} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1 \end{pmatrix} \right|\]

Where (x1, y1), (x2, y2), and (x3, y3) are the coordinates of the vertices of the triangle.

Importance of Determinants Class 12 Notes

The importance of Class 12 Determinants notes lies in their role as a comprehensive and accessible resource for mastering a key mathematical concept that is essential for both academic success and future studies. Here’s why these notes are crucial:

1. Simplified Learning: Determinants can be a complex topic, but well-structured notes break down the concepts into manageable sections, making it easier for students to understand and remember.

2. Exam Preparation: The notes highlight important formulas, properties, and problem-solving techniques that are frequently tested in board exams, ensuring students are well-prepared and confident.

3. Foundation for Higher Studies: Determinants form the basis for many advanced topics in mathematics, physics, and engineering. Mastery of this chapter is essential for success in competitive exams like JEE and for future coursework in these fields.

4. Quick Revision: The notes provide a concise summary of key concepts, making them an ideal tool for quick revision before exams. This helps in reinforcing learning and recalling important points during the exam.

5. Problem-Solving Skills: By working through examples and exercises included in the notes, students can enhance their analytical and problem-solving skills, which are crucial for tackling complex questions in exams.

Tips for Learning the Class 12 Maths Chapter 4 Determinants

Here are some helpful tips for learning Class 12 Maths Chapter 4 Determinants:

1. Understand the Basics: Start by revisiting the basic concepts of matrices, as understanding these is crucial before diving into determinants. Ensure you are comfortable with operations like addition, multiplication, and finding the inverse of matrices.

2. Memorise Key Formulas: Make sure to memorise the key formulas related to determinants, such as those for 2x2 and 3x3 matrices, properties of determinants, and the calculation of minors and cofactors. These are foundational for solving problems.

3. Practice Cofactors and Minors: Spend extra time practising how to find the minor and cofactor of elements within a matrix. This skill is essential when calculating the determinant of larger matrices and finding the inverse of a matrix.

4. Work Through Examples: Go through solved examples in your textbook or notes to see how the formulas and properties of determinants are applied in different types of problems. This will help you understand the step-by-step process required to solve similar questions.

5. Use Visual Aids: Visualize the concepts by drawing matrices and marking the rows and columns you are working with when calculating minors, cofactors, and determinants. This can help in keeping track of the elements and operations.

6. Understand Properties: Focus on understanding the properties of determinants, such as the effect of row and column operations, the determinant of a product, and the relationship between the determinant of a matrix and its transpose. These properties are useful shortcuts in solving problems.

Conclusion

Mastering the topic of determinants is essential for success in Class 12 Mathematics and beyond. The comprehensive notes on determinants provide clear explanations, key formulas, and step-by-step problem-solving techniques that simplify this complex subject. By using these notes for study and revision, students can build a strong understanding of determinants, enhance their problem-solving skills, and approach exams with confidence. These notes not only prepare students for board exams but also lay a solid foundation for higher studies in mathematics, engineering, and related fields.

Related Study Materials for Class 12 Maths Chapter 4 Determinants

Students can also download additional study materials provided by Vedantu for Class 12 Maths Chapter 4 Determinants:

Chapter-wise Revision Notes Links for Class 12 Maths

Important Study Materials for Class 12 Maths