Download Free PDF of Application of Integrals Miscellaneous Exercise for Class 12 Maths
If you’re preparing for CBSE Board exams and want complete confidence in calculus, these NCERT Solutions for Class 12 Maths Chapter 8 Miscellaneous Exercise are designed for you. This section brings together critical application questions on integration, focusing especially on areas under curves and methods to find the area between two functions. With attentive explanations, each step matches the latest board marking scheme for 2025.
Table of Content
Questions in this miscellaneous exercise challenge you with calculation-rich scenarios and real-life contexts. Students often ask how to solve area between curves problems for CBSE Board or search for application of integrals class 12 miscellaneous solutions that simplify visualising bounded regions. Here, you’ll find answers that break down these advanced applications clearly.
Scoring is strategic too—Application of Integrals carries a reliable weightage of 6 marks each year and is a must-practice for full marks. Vedantu’s expert-reviewed stepwise solutions and exam-ready tricks help you master definite integrals and avoid common mistakes, making your revision targeted and efficient. For complete coverage, always refer to the Class 12 Maths syllabus as per the latest CBSE guidelines.
Miscellaneous Exercise
1. Find the area under the given curves and given lines:
(i) \[\text{y=}{{\text{x}}^{\text{2}}}\text{,x=1,x=2}\] and \[\text{x-axis}\]
Ans:
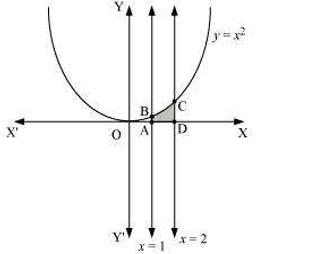
\[\text{AreaADCBA=}\int_{\text{1}}^{\text{2}}{\text{y}}\text{dx}\]
substitute $y={{x}^{2}}$
\[\text{=}\int_{\text{1}}^{\text{2}}{{{\text{x}}^{\text{2}}}}\text{dx}\]
Substituting the limits,
\[\text{=}\frac{\text{8}}{\text{3}}\text{-}\frac{\text{1}}{\text{3}}\]
\[\text{=}\frac{\text{7}}{\text{3}}\text{units}\]
(ii) \[\text{y=}{{\text{x}}^{4}}\text{,x=1,x=5}\] and \[\text{x-axis}\]
Ans:
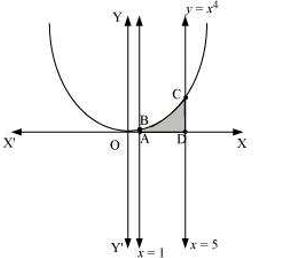
\[\text{AreaofADCBA=}\int_{\text{1}}^{\text{5}}{{{\text{x}}^{\text{4}}}}\text{dx}\]
Integrating using the power rule,
\[\text{=}\left[ \frac{{{\text{x}}^{\text{5}}}}{\text{5}} \right]_{\text{1}}^{\text{5}}\]
Substituting the limits,
\[\text{=}\frac{{{\text{(5)}}^{\text{5}}}}{\text{5}}\text{-}\frac{\text{1}}{\text{5}}\]
Simplifying,
\[\text{=(5}{{\text{)}}^{\text{4}}}\text{-}\frac{\text{1}}{\text{5}}\]
\[\text{=625-}\frac{\text{1}}{\text{5}}\]
\[\text{=624}\text{.8 units}\]
2. Sketch the graph of \[\text{y=}\left| \text{x+3} \right|\] and evaluate \[\int_{-6}^{0}{\left| \text{x+3} \right|}\text{dx}\].
Ans:
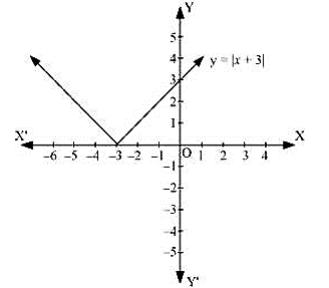
\[\left( \text{x+3} \right)\le 0\] for \[\text{-6}\le \text{x}\le \text{-3}\]
\[\left( \text{x+3} \right)\ge \text{0}\] for \[\text{-3}\le \text{x}\le 0\]
Therefore,
\[\int_{\text{-6}}^{\text{0}}{\text{ }\!\!|\!\!\text{ }}\text{(x+3) }\!\!|\!\!\text{ dx=-}\int_{\text{-6}}^{\text{-3}}{\text{(x+3)}}\text{dx+}\int_{\text{-3}}^{\text{0}}{\text{(x+3)}}\text{dx}\]
Integrating using the power rule
\[\text{= -}\left[ \frac{{{\text{x}}^{\text{2}}}}{\text{2}}\text{+3x} \right]_{\text{-6}}^{\text{-3}}\text{+}\left[ \frac{{{\text{x}}^{\text{2}}}}{\text{2}}\text{+3x} \right]_{\text{-3}}^{\text{0}}\]
Substituting the limits,
\[\text{=-}\left[ \left( \frac{{{\text{(-3)}}^{\text{2}}}}{\text{2}}\text{+3(-3)} \right)\text{-}\left( \frac{{{\text{(-6)}}^{\text{2}}}}{\text{2}}\text{+3(-6)} \right) \right]\text{+}\left[ \text{0-}\left( \frac{{{\text{(-3)}}^{\text{2}}}}{\text{2}}\text{+3(-3)} \right) \right]\]
Simplifying,
\[\text{= -}\left[ \text{-}\frac{\text{9}}{\text{2}} \right]\text{-}\left[ \text{-}\frac{\text{9}}{\text{2}} \right]\]
\[\text{=9}\]
3. Find the area bounded by the curve \[\text{y=sinx}\] between \[\text{x=0}\] and \[\text{x=2 }\!\!\pi\!\!\text{ }\].
Ans:
Therefore, \[\text{area = Area OABO+ Area BCDB}\]
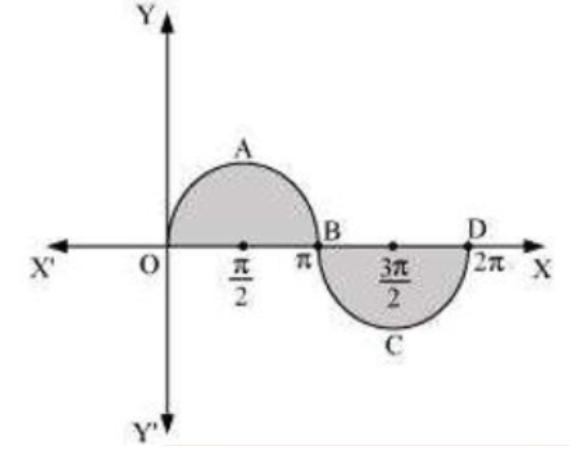
Area Bounded by Curve y=sinx
\[\text{=}\int_{\text{0}}^{\text{ }\!\!\pi\!\!\text{ }}{\text{sin}}\text{xdx+}\left| \int_{\text{ }\!\!\pi\!\!\text{ }}^{\text{2 }\!\!\pi\!\!\text{ }}{\text{sin}}\text{xdx} \right|\]
\[\text{= }\!\![\!\!\text{ -cosx }\!\!]\!\!\text{ }_{\text{0}}^{\text{ }\!\!\pi\!\!\text{ }}\text{+}\left| \text{ }\!\![\!\!\text{ -cosx }\!\!]\!\!\text{ }_{\text{ }\!\!\pi\!\!\text{ }}^{\text{2 }\!\!\pi\!\!\text{ }} \right|\]
Substituting the limits,
\[\text{= }\!\![\!\!\text{ -cos }\!\!\pi\!\!\text{ +cos0 }\!\!]\!\!\text{ + }\!\!|\!\!\text{ -cos2 }\!\!\pi\!\!\text{ +cos }\!\!\pi\!\!\text{ }\!\!|\!\!\text{ }\]
Simplifying,
\[\text{=1+1+ }\!\!|\!\!\text{ (-1-1) }\!\!|\!\!\text{ }\]
\[\text{=2+ }\!\!|\!\!\text{ -2 }\!\!|\!\!\text{ }\]
\[\text{=2+2}\]
\[\text{=4 units}\]
4. Area bounded by the curve \[\text{y=}{{\text{x}}^{3}}\], the \[\text{x-axis}\] and the ordinates \[\text{x = -2}\] and \[\text{x = 1}\] is
A. \[\text{-9}\]
B. \[\text{-}\frac{\text{15}}{\text{4}}\]
C. \[\frac{\text{15}}{\text{4}}\]
D. \[\frac{\text{17}}{\text{4}}\]
Ans:
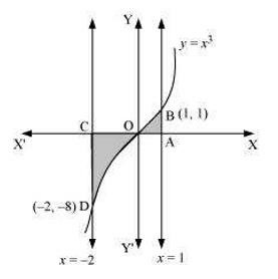
As shown in the diagram, the required area is:
\[\text{Required area =}\int_{\text{-2}}^{\text{1}}{\text{y}}\text{dx}\]
\[\text{=}\int_{\text{-2}}^{\text{1}}{{{\text{x}}^{\text{3}}}}\text{dx}\]
Integrating using the power rule
\[\text{=}\left[ \frac{{{\text{x}}^{\text{4}}}}{\text{4}} \right]_{\text{-2}}^{\text{1}}\]
Substituting the limits,
\[\text{=}\left[ \frac{\text{1}}{\text{4}}\text{-}\frac{{{\text{(-2)}}^{\text{4}}}}{\text{4}} \right]\]
Simplifying,
\[\text{=}\left( \frac{\text{1}}{\text{4}}\text{-4} \right)\]
\[\text{= -}\frac{\text{15}}{\text{4}}\text{ units}\]
So, the correct answer is \[\text{ -}\frac{\text{15}}{\text{4}}\text{ units}\] option B.
5. The area bounded by the curve \[\text{y=x}\left| \text{x} \right|\text{,x-axis}\] and the ordinate \[\text{x = 1}\] and \[\text{x = -1}\] is given by (Hint \[\text{y = }{{\text{x}}^{2}}\] if \[x>0\] and \[\text{y = -}{{\text{x}}^{2}}\] if \[x<0\])
A. \[0\]
B. \[\frac{\text{1}}{\text{3}}\]
C. \[\frac{2}{\text{3}}\]
D. \[\frac{4}{\text{3}}\]
Ans:
\[\text{Required area=}\int_{\text{-1}}^{\text{1}}{\text{y}}\text{dx}\]
\[\text{=}\int_{\text{-1}}^{\text{1}}{\text{x}}\text{ }\!\!|\!\!\text{ x }\!\!|\!\!\text{ dx}\]
\[\text{= -}\int_{\text{-1}}^{\text{0}}{{{\text{x}}^{\text{2}}}}\text{dx+}\int_{\text{0}}^{\text{1}}{{{\text{x}}^{\text{2}}}}\text{dx}\]
Integrating using the power rule
\[\text{= -}\left[ \frac{{{\text{x}}^{\text{3}}}}{\text{3}} \right]_{\text{-1}}^{\text{0}}\text{+}\left[ \frac{{{\text{x}}^{\text{3}}}}{\text{3}} \right]_{\text{0}}^{\text{1}}\]
Substituting the limits,
\[\text{= -}\left( \text{-}\frac{\text{1}}{\text{3}} \right)\text{+}\frac{\text{1}}{\text{3}}\]
\[\text{=}\frac{\text{2}}{\text{3}}\text{units}\]
So, the correct answer is \[\frac{\text{2}}{\text{3}}\text{units}\] option C.
Conclusion
The Class 12 Maths Chapter 8 Miscellaneous Exercise Solutions is important for understanding various concepts thoroughly. Application of Integrals Class 12 Miscellaneous includes a variety of issues that call for the use of several formulas and methods. It's crucial to concentrate on comprehending the fundamental ideas behind every question, as opposed to merely learning the answers by heart. To successfully complete this task, keep in mind that you must comprehend the theory underlying each idea, practise frequently, and consult solved examples.
Class 12 Maths Chapter 8: Exercises Breakdown
CBSE Class 12 Maths Chapter 8 Other Study Materials
Chapter-Specific NCERT Solutions for Class 12 Maths
Given below are the chapter-wise NCERT Solutions for Class 12 Maths. Go through these chapter-wise solutions to be thoroughly familiar with the concepts.
FAQs on CBSE Class 12 Mathematics Chapter 8 Application of Integrals – NCERT Solutions 2025-26
1. What are the important topics covered in Class 12 Maths Chapter 8 miscellaneous exercise?
Class 12 Maths Chapter 8 miscellaneous exercise focuses on application-based questions in integrals as per the CBSE 2025 syllabus. Key topics include:
- Area under curves using definite integrals
- Area between two curves and lines
- Setting limits of integration in real-life contexts
- Interpreting and sketching regions for calculation
- Application of integrals in Board exams and competitive entrance questions
2. How do I download the NCERT Solutions PDF for application of integrals?
To download the NCERT Solutions PDF for Class 12 Maths Chapter 8 (Application of Integrals):
- Visit trusted platforms like Vedantu's solution page for Miscellaneous Exercise
- Look for the “Download Free NCERT Solutions PDF” button or link
- Click the button to save the solution PDF for Board and competitive exam preparation
- Ensure the solutions use the latest CBSE 2025 syllabus
3. What is the easiest way to solve area between curves problems for CBSE Board?
The simplest way to solve area between curves problems in CBSE Board exams is to use the definite integral method:
- Identify the two curves and sketch the bounded region
- Find the intersection points to determine limits of integration
- Set up the definite integral: ∫ab [Upper function – Lower function] dx
- Evaluate the definite integral step-by-step
- Express the answer with correct units and mention the region
This approach follows the CBSE marking scheme and mirrors patterns in the NCERT Solutions for Class 12 Maths Chapter 8 Miscellaneous Exercise.
4. Why should I use Vedantu's solutions over other guides?
Vedantu's NCERT Solutions for Class 12 Maths are trusted because:
- Created by experienced educators using the latest CBSE 2025 syllabus
- Provide stepwise, exam-aligned solutions with clear formulas and boxed answers
- Include downloadable PDFs for easy revision and last-minute preparation
- Offer concept clarity through well-explained diagrams and highlighted methods
- Regularly fact-checked for accuracy by syllabus experts
5. Is the miscellaneous exercise in Chapter 8 important for competitive exams like JEE or NEET?
Yes, the miscellaneous exercise of Application of Integrals is highly important for JEE, NEET, and other entrance exams because:
- It covers complex, application-oriented integration problems similar to those asked in entrance tests
- Practicing these solutions enhances problem-solving skills needed for MCQs and descriptive Qs
- Questions on area under curves and between curves regularly appear in JEE Main and NEET calculus sections
6. How can I score full marks in application of integrals questions in the 2025 Board exam?
To score full marks in Class 12 Maths Application of Integrals questions:
- Follow CBSE-approved, step-by-step solving methods from the NCERT Miscellaneous Exercise
- Clearly box final answers and state units
- Draw neat sketches of regions/curves when required
- Avoid common mistakes in setting integration limits and calculating area
- Revise important formulas and practice previous year Board questions
7. How do I solve area under curve problems using application of integrals?
Solve area under curve problems by applying definite integration as follows:
- Identify the curve and the interval [a, b] for the required area
- Set up the integral ∫ab f(x) dx
- Evaluate the definite integral stepwise
- State the area with proper units and mention the region
This method forms the foundation of Chapter 8 Miscellaneous Exercise solutions and appears in both Board and competitive exam patterns.
8. What is chapter 8 of maths class 12?
Chapter 8 of Class 12 Maths is titled "Application of Integrals". It focuses on:
- Finding the area under curves and between curves using definite integrals
- Real-life application-based word problems
- Visualization and calculation of bounded regions
- CBSE Board and JEE/NEET exam questions
9. What is the formula for area between two curves in application of integrals?
The standard formula for area between two curves y = f(x) and y = g(x) from x = a to x = b is:
- Area = ∫ab [f(x) – g(x)] dx, where f(x) ≥ g(x) throughout [a, b]
- Correct limits and identification of curves are crucial as per CBSE 2025 syllabus
- Frequently used in NCERT Solutions for Class 12 Maths Chapter 8 Miscellaneous Exercise
10. Which is the hardest chapter in class 12 maths?
In the Class 12 Maths syllabus, students often find chapters like Integration, Application of Integrals, and Probability challenging due to their abstract concepts and application-based problems:
- Application of Integrals requires clarity in setting up definite integrals and interpreting diagrams
- Mastery comes through practice of NCERT Miscellaneous Exercises and solving previous year Board questions
