NCERT Solutions for Class 12 Chemistry In Hindi Chapter 2 Solutions Hindi Medium

1. विलयन को परिभाषित कीजिए। कितने प्रकार के विभिन्न विलयन सम्भव हैं? प्रत्येक प्रकार के विलयन के सम्बन्ध में एक उदाहरण देकर संक्षेप में लिखिए।

उत्तर:

विलयन- विलयन दो या दो से अधिक अवयवों का समांगी मिश्रण होता है जिसका संघटन निश्चित परिसीमाओं के अन्तर्गत ही परिवर्तित हो सकता है। यहाँ समांगी मिश्रण से तात्पर्य यह है कि मिश्रण में सभी स्थानों पर इसका संघटन व गुण समान होते हैं। विलयन को बनाने वाले पदार्थ विलयन के अवयव कहलाते हैं। किसी विलयन में उपस्थित अवयवों की कुल संख्या के आधार पर इन्हें द्विअंगी विलयन (दो अवयव), त्रिअंगी विलयन (तीन अवयव), चतुरंगी विलयन (चार अवयव) आदि कहा जाता है। द्विअंगी विलयन के अवयवों को सामान्यतः विलेय तथा विलायक कहा जाता है। सामान्यतः जो अवयव अधिक मात्रा में उपस्थित होता है, वह विलायक कहलाता है, जबकि कम मात्रा में उपस्थित अन्य अवयव विलेय कहलाता है। विलायक विलयन की भौतिक अवस्था निर्धारित करता है जिसमें विलयन विद्यमान होता है। दूसरे शब्दों में विलेय वह पदार्थ होता है जो घुलता है तथा विलायक वह पदार्थ है जिसमें यह विलेय घुलता है।

उदाहरणार्थ- यदि चीनी के कुछ क्रिस्टलों को जल से भरे बीकर में डाल दिया जाए तो ये जल में घुलकर विलयन बना जायेंगे। इस स्थिति में चीनी विलेय तथा जल विलायक कहलाएगा। विलयन में कणों का आण्विक आकार लगभग $1000pm$ होता है तथा इसके विभिन्न अवयवों को किसी भी भौतिक विधि जैसे फिल्टरीकरण, निथारन, अभिकेन्द्रीकरण आदि के द्वारा पृथक्कृत नहीं किया जा सकता है।

विलयन के प्रकार है (Types of solution) - विलेय तथा विलायक की भौतिक अवस्था के आधार पर विलयनों को निम्नलिखित प्रकारों में वर्गीकृत किया जा सकता है –

उपयुक्त नौ प्रकार के विलयनों में से तीन विलयन- द्रव में ठोस, द्रव में गैस तथा द्रव में द्रव अतिसामान्य विलयन हैं। इन तीनों प्रकार के विलयनों में द्रव विलायक के रूप में होता है। वे विलयन जिसमे जल घुलने के रूप में होता है, जलीय विलयन (aqueous solution) कहलाते हैं, जबकि जिन विलयनों में जल घुलने के रूप में नहीं होता अजलीय विलयन (non-aqueous solution) कहलाते हैं। सामान्य

अजलीय विलायकों के उदाहरण हैं- ईथर, बेन्जीन, कार्बन टेट्राक्लोराइड आदि। विलयन के प्रकारों की व्याख्या निम्नलिखित है –

1) गैसीय विलयन (Gaseous solutions) - सभी गैसें तथा वाष्प समांगी मिश्रण बनाती हैं तथा इसीलिए इन्हें विलयन कहा जाता है। ये विलयन स्वतः और तीव्रता से बनते हैं। वायु गैसीय विलयन का एक अच्छा उदाहरण है।

(2) द्रव विलयन (Liquid solutions)- ये विलयन ठोसों और गैसों को द्रवों में मिश्रित करने पर अथवा दो द्रवों को मिश्रित करने पर बनते हैं। कुछ ठोस पदार्थ भी मिश्रित करने पर द्रव विलयन बनाते हैं। उदाहरणार्थ- साधारण ताप पर सोडियम तथा पोटैशियम धातुओं की सममोलर मात्राएँ मिश्रित करने पर द्रव विलयन प्राप्त होता है। जल में पर्याप्त मात्रा में विलेय ऑक्सीजन तालाबों, नदियों एवम समुद्र में जल मै रेह्ने वाले जीवों की प्राण-रक्षा करती है। इन विलयनों में द्रव में द्रव विलयन बहुत महत्त्वपूर्ण हैं। गैसों के समान द्रव मिश्रित किए जाने पर समांगी मिश्रण नहीं बनाते हैं। इनकी विलेयताओं के आधार पर इन मिश्रणों को तीन प्रकारों में बाँटा गया है:

1. जब दोनों अवयव पूर्णतया मिश्रणीय हों 

(When both components are completely miscible) - इस स्थिति में दोनों द्रव समान प्रवृत्ति के होते हैं अर्थात् या तो ये दोनों ध्रुवी (जैसे-एथिल ऐल्कोहॉल तथा जल) होते हैं या अध्रुवी (जैसे—बेन्जीन तथा हेक्सेन) होते हैं।

2. जब दोनों अवयव लगभग मिश्रणीय हों (When both components are almost miscible)- यहाँ एक द्रव ध्रुवी तथा दूसरा अध्रुवी प्रकृति का होता है; जैसे-बेन्जीन तथा जल, तेल तथा जल आदि।

3. जब दोनों अवयव आंशिक मिश्रणीय हों (When both components are partially miscible) - यदि द्रव $A$ में अन्तरअणुक आकर्षण $A - A$, द्रव $B$ में अन्तरअणुक आकर्षण $B - B$ से भिन्न हो, परन्तु $A - B$ आकर्षण माध्यमिक कोटि का हो, तब दोनों द्रव परस्पर सीमित मिश्रणीय होते हैं। उदाहरणार्थ-ईथर तथा जल आंशिक रूप से मिश्रित होते हैं।

(3) ठोस विलयन (Solid solutions)- ठोसों के मिश्रणों की स्थिति में ये विलयन अत्यन्त सामान्य होते हैं। उदाहरणार्थ- गोल्ड तथा कॉपर ठोस विलयन बनाते हैं; क्योंकि गोल्ड परमाणु कॉपर क्रिस्टल में कॉपर परमाणुओं को प्रतिस्थापित कर देते हैं और इसी प्रकार कॉपर परमाणु गोल्ड क्रिस्टलों में गोल्ड परमाणुओं को बदल सकते हैं। दो अथवा दो से अधिक धातुओं की मिश्रधातुएँ ठोस विलयन होती हैं। ठोस विलयनों को दो वर्गों में बाँटा जा सकता है –

1. प्रतिस्थापनीय ठोस विलयन (Substitutional solid solutions)- इन विलयनों में एक पदार्थ के परमाणु, अणु अथवा आयन क्रिस्टल जालक में अन्य पदार्थ के कणों का स्थान ले लेते हैं। प्रतिस्थापनीय ठोस विलयनों का समान्य उदाहरण इस प्रकार है पीतल, कॉपर तथा जिंक।

2. अन्तराकाशी ठोस विलयन (Interstitial solid solutions) - इन विलयनों में एक प्रकार के परमाणु अन्य पदार्थ के परमाणुओं के जालक में विद्यमान रिक्तिकाओं अथवा अन्तराकाशों के स्थान को ग्रहण कर लेते हैं। अन्तराकाशी ठोस विलयन का एक सामान्य उदाहरण टंगस्टन-कार्बाइड (WC) है।

2. एक ऐसे ठोस विलयन का उदाहरण दीजिए जिसमें विलेय कोई गैस हो।

उत्तर: जैसे कहा जाता है कि एक पदार्थ के कण दूसरे पदार्थ के कणों की तुलना में बहुत छोटे होते हैं, अतः छोटे कण बड़े कणों के अन्तराकाशी स्थलों में व्यवस्थित हो जायेंगे। अतः ठोस विलयन अन्तराकाशी ठोस विलयन (interstitial solid solution) प्रकार का होगा।

3. निम्न पदों को परिभाषित कीजिए -

1. मोल-अंश 

उत्तर: मोल-अंश (Mole-Fraction) - विलयन में उपस्थित किसी एक घटक या अवयव के मोलों की संख्या और विलेय एवं विलायक के कुल मोलों की संख्या के अनुपात को उस अवयव का मोल-अंश कहा जाता हैं। इसे $x$ से व्यक्त करते हैं। माना एक विलयन में विलेय के ${n_B}$ मोल तथा विलायक के ${n_A}$ मोल उपस्थित हैं, तब

विलेय के मोल अंश $\left( {{x_A}} \right)$$ = \dfrac{{{n_A}}}{{{n_A} + {n_B}}}$
विलायक के मोल-अंश $\left( {{x_B}} \right) = \dfrac{{{n_B}}}{{{n_A} + {n_B}}}$
विलयन में समस्त अवयवों के मोल-अंशों का योग सदैव 1 होता है, अर्थात्

${x_A} + {x_B} = \dfrac{{{n_A}}}{{{n_A} + {n_B}}} + \dfrac{{{n_B}}}{{{n_A} + {n_B}}} = 1$

अतः यदि किसी द्विअंगी विलयन के एक अवयव के मोल-अंश मालूम हों तो दूसरे अवयव के मोल-अंश मालूम किया जा सकता हैं। उदाहरणार्थ-द्विअंगी विलयन के लिए मोल-अंश ${X_{A,}}{X_B}$ से निम्नलिखित प्रकार सम्बन्धित है

${X_A} = 1 - {X_B}$  या ${X_B} = 1 - {X_A}$

मोल- अंश विलयन के ताप पर निर्भर नहीं करते हैं।मोललता $(m) = x1000$

2. मोललता

उत्तर: मोललता (Molality) – किसी विलयन के $1kg$ विलायक में उपस्थित विलेय के मोलों की संख्या विलयन की मोललता कहलाती है। इसे $m$ से व्यक्त किया जाता है। गणितीय रूप में, विलेय के मोल विलेय के मोल विलायक का $kg$ में भार विलायक का $g$ में भार अत: मोललता की इकाई मोल प्रति किग्रा $({\mathbf{mol}}{\text{ }}{\mathbf{k}}{{\mathbf{g}}^{ - {\mathbf{1}}}})$होती है।

यदि विलेय के ${n_B}$  मोल विलायक के $W$ ग्राम में घुले हों, तब मोललता $ = {n_{\dfrac{B}{W}}} \times 1000$

3. मोलरता

उत्तर: मोलरता (Molarity) - एक लीटर ($1$ क्यूबिक डेसीमीटर) विलयन में घुले हुए विलेय के मोलों की संख्या को उस विलयन की मोलरता $(M)$ कहते हैं।

अतः वह विलयन जिसमें विलेय के एक ग्राम- मोल विलयन के एक लीटर में उपस्थित हों, $1M$ विलयन कहलाता है। उदाहरणार्थ- $1M - N{a_2}C{o_3}$ (मोलर द्रव्यमान $ = 106$) विलयन के प्रति लीटर में $106g$ विलेय उपस्थित होता है।

 मोलरता = विलेय के मोल / विलयन का आयतन (लीटर में ) 

आयतन को सामान्यतया $c{m^3}$ या mL में व्यक्त किया जाता है। अतः

 मोलरता = विलेय के मोल / विलयन का आयतन ($mL$ या $c{m^3}$ में) $ \times 1000$

अतः मोलरता की इकाई मोल प्रति लीटर ($mol$ ${L^{ - 1}}$) या मोल प्रति घन डेसीमीटर ($mol$ $d{m^{ - 3}}$) होती हैं। प्रतीक $M$ को $mol$ ${L^{ - 1}}$ अथवा $mol$ $d{m^{ - 3}}$ के लिए प्रयोग किया जाता है तथा यह मोलरता व्यक्त करता है।

यदि विलेय के ${n_B}$ मोल विलयन के $V$ $mL$ आयतन में उपस्थित हों, तब 

मोलरता $(M) = x1000$

विलेय के मोल निम्नलिखित प्रकार ज्ञात किए जा सकते हैं –

विलेय के मोल = विलेय का द्रव्यमान / विलेय का मोलर द्रव्यमान 

मोलरता सान्द्रता व्यक्त करने की एक साधारण माप है जिसे प्रयोगशाला में सामान्यतया प्रयोग किया जाता है। यद्यपि इसमें एक कमी है, यह ताप के साथ परिवर्तित हो जाती है क्योंकि ताप के साथ द्रव का प्रसार अथवा संकुचन हो जाता है।

4. द्रव्यमान प्रतिशत

उत्तर: द्रव्यमान प्रतिशत (Mass Percentage) – किसी विलयन में किसी अवयव का द्रव्यमान प्रतिशत विलयन के प्रति $100g$ में उस अवयव का द्रव्यमान होता है। उदाहरणार्थ– यदि विलयन में अवयव $A$ का द्रव्यमान ${W_A}$ तथा अवयव $B$ को द्रव्यमान ${W_B}$  हो तो

$A$ का द्रव्यमान प्रतिशत $ = \dfrac{{{W_A}}}{{{W_A} + {W_B}}} \times 100$

इसे $\dfrac{w}{w}$ से प्रस्तुत किया जाता है। उदाहरणार्थ- $ - 10\% \left( {\dfrac{w}{w}} \right)$  सोडियम क्लोराइड विलयन का अर्थ है। कि $10g$ सोडियम क्लोराइड $90g$ जल में उपस्थित है तथा विलयन का कुल द्रव्यमान $100g$ है अथवा $10g$ सोडियम क्लोराइड $100g$ विलयन में उपस्थित है।

4. प्रयोगशाला कार्य के लिए प्रयोग में लाया जाने वाला सान्द्र नाइट्रिक अम्ल द्रव्यमान की दृष्टि से नाइट्रिक अम्ल का $68\% $ जलीय विलयन है। यदि इस विलयन का घनत्व $1.504$ $g$ $m{L^{ - 1}}$ हो तो अम्ल के इस नमूने की मोलरता क्या होगी?

उत्तर: द्रव्यमानानुसार $68\% $ $HN{O_3}$ का तात्पर्य है कि $100g$ विलयन में $68g$ $HN{O_3}$उपस्थित होगा

$68g$ $HN{O_3}$$ = \dfrac{{68}}{{63}}$ $mol$

$ = 1.079$ $mol$

विलयन का आयतन   = विलयन का भार / घनत्व 

$ = \dfrac{{100}}{{1.504}}$

$ = 66.49$ $mL$

मोलरता $(M)\; = HN{O_3}\;$के मोल  विलयन का आयतन लीटर में    

$ = 1.079 \times \dfrac{{100}}{{066.49}}$

$ = 16.23M$

5. ग्लूकोस का एक जलीय विलयन $10\% \left( {\dfrac{w}{w}} \right)$ है। विलयन की मोललता तथा विलयन में प्रत्येक घटक का मोल-अंश क्या है? यदि विलयन का घनत्व ${\mathbf{1}}.{\mathbf{2}}{\text{ }}{\mathbf{g}}{\text{ }}{\mathbf{m}}{{\mathbf{L}}^{ - {\mathbf{1}}}}$ हो तो विलयन की मोलरता क्या होगी?

उत्तर:

$10\% \left( {\dfrac{w}{w}} \right)$ ग्लूकोस विलयन का तात्पर्य है कि $100g$ ग्लूकोस विलयन में $10$ ग्लूकोस उपस्थित होगा।

जल का द्रव्यमान 

$ = 100 - 10$

$ = 90g$

$ = {\text{ }}0.090{\text{ }}kg$

$10g$ ग्लूकोस 

$ = \dfrac{{10}}{{180}}{\text{ }}mol$

$ = {\text{ }}0.0555{\text{ }}mol$

${\mathbf{90}}{\text{ }}{\mathbf{g}}{\text{ }}{{\mathbf{H}}_{\mathbf{2}}}{\mathbf{O}}$

$ = \;\dfrac{{90}}{{18}}$

$ = {\text{ }}5{\text{ }}mol$

मोललता $\left( {\mathbf{m}} \right) = \dfrac{{0.0555}}{{0.090}}$

$ = {\text{ }}0.617{\text{ }}m$

ग्लूकोस का मोल प्रभाज $ = \dfrac{{\dfrac{{10}}{{180}}}}{{\dfrac{{10}}{{180}} + \dfrac{{90}}{{18}}}}$

$ = 0.011$

जल का मोल प्रभाज $ = \dfrac{{\dfrac{{90}}{{18}}}}{{\dfrac{{10}}{{180}} + \dfrac{{90}}{{18}}}}$

$ = 0.989\;$ $100{\text{ }}g\;$

विलयन $ = \dfrac{{100}}{{1.2}}{\text{ }}mL$

$ = 83.33{\text{ }}mL$

$ = 0.08333{\text{ }}L\;$

मोलरता $ = \dfrac{{0.0555{\text{ }}mol}}{{0.08333{\text{ }}L}}$

$ = 0.67M$

6. यदि ${\mathbf{1}}{\text{ }}{\mathbf{g}}$ मिश्रण में ${\mathbf{N}}{{\mathbf{a}}_{\mathbf{2}}}{\mathbf{C}}{{\mathbf{O}}_{\mathbf{3}}}$ एवं ${\mathbf{NaHC}}{{\mathbf{O}}_{\mathbf{3}}}$ के मोलों की संख्या समान हो तो इस मिश्रण से पूर्णतः क्रिया करने के लिए ${\mathbf{0}}.{\mathbf{1}}{\text{ }}{\mathbf{M}}{\text{ }}{\mathbf{HCl}}\;$के कितने ${\mathbf{mL}}$ की आवश्यकता होगी?

उत्तर:

$N{a_2}C{O_3}$  तथा $NaHC{O_3}$ के मिश्रण का भार $ = 1g$

माना की मिश्रण में $N{a_2}C{O_3}$ के $xg$ उपस्थित हैं।
अत: $NaHC{O_3}$ की मात्रा $ = \left( {1 - x} \right)g$
∴$N{a_2}C{O_3}$ के मोल $ = \dfrac{x}{{106}}$($N{a_2}C{O_3}$ का अणुभार $ = 106$)
∴ $NaHC{O_3}$ के मोल $ = \dfrac{{1 - x}}{{84}}$
(∵$NaHC{O_3}$ का अणुभार $ = 84$)
चूँकि मिश्रण सममोलर है,
अत:
$\dfrac{x}{{106}} = \dfrac{{1 - x}}{{84}}$
या
$x = \dfrac{{106}}{{190}}g$
$N{a_2}C{O_3}$ का मिश्रण में द्रव्यमान $ = \dfrac{{106}}{{190}}$
$NaHC{O_3}$ का मिश्रण में द्रव्यमान $ = 1 - \dfrac{{106}}{{190}}$

$ = \dfrac{{84}}{{190}}$

$N{a_2}C{O_3} + 2HCl \to 2NaCl + C{O_2} + {H_2}O$  $1$ मोल  $2$ मोल   

$NaHC{O_3} + HCl \to NaCl + C{O_2} + {H_2}O\;$ $1$ मोल  $1$ मोल 
$106gN{a_2}C{O_3}$ के पूर्ण उदासीनीकरण के लिए आवश्यक $HCl = 2\;mol$
$\therefore {\text{ }}\dfrac{{106}}{{190}}gN{a_2}C{O_3}$ के पूर्ण उदासीनीकरण के लिए आवश्यक HCl

$ = \dfrac{2}{{106}} \times \dfrac{{106}}{{190}}$

$ = \dfrac{2}{{190}}mol$

$84g NaHC{O_3}$ के पूर्ण उदासीनीकरण के लिए आवश्यक $HCl = 1mol$

$\therefore \dfrac{{84}}{{190}}gNaHC{O_3}$ के पूर्ण उदासीनीकरण के लिए आवश्यक $HCl = \dfrac{1}{{84}} \times \dfrac{{84}}{{190}}$

$ = \dfrac{1}{{190}}mol$

अत:$\;HCl$ के कुल आवश्यक मोल $ = \dfrac{2}{{190}} + \dfrac{1}{{190}} = \dfrac{3}{{190}}mol$ आवश्यक $0.1MHCl$का आयतन $ = 1000 \times \dfrac{3}{{190}} \times 10$

$ = 157.8{\text{ }}mL$

7. द्रव्यमान की दृष्टि से ${\mathbf{25}}\% $ विलयन के ${\mathbf{300}}{\text{ }}{\mathbf{g}}$ एवं ${\mathbf{40}}\% $ के ${\mathbf{400}}{\text{ }}{\mathbf{g}}$ को आपस में मिलाने पर प्राप्त मिश्रण का द्रव्यमान प्रतिशत सान्द्रण निकालिए।
उत्तर:

$25\% $ विलयन का तात्पर्य है कि $25{\text{ }}g$ विलेय $100{\text{ }}g$ विलयन में उपस्थित है तथा $40\% $ विलयन का तात्पर्य है कि $40{\text{ }}g$ विलेय $100{\text{ }}g$ विलयन में उपस्थित है।
$300{\text{ }}g$ विलयन में विलेय 

$ = \dfrac{{{\mathbf{25}} \times {\mathbf{300}}}}{{{\mathbf{100}}}}$

$ = \;{\text{ }}75{\text{ }}g$

$400{\text{ }}g$ विलयन में विलेय 

$ = \dfrac{{40 \times 400}}{{100}}$

$\; = {\text{ }}160{\text{ }}g$
∴ विलेय का कुल द्रव्यमान 

$ = 75 + 160$

$ = {\text{ }}235{\text{ }}g$
∴ मिश्रण में विलेय का द्रव्यमान प्रतिशत 

$ = \dfrac{{235 \times 100}}{{700}}$  

$ = 33.57\% $

8. ${\mathbf{222}}.{\mathbf{6}}{\text{ }}{\mathbf{g}}$, एथिलीन ग्लाइकॉल, ${{\mathbf{C}}_{\mathbf{2}}}{{\mathbf{H}}_{\mathbf{4}}}{\left( {{\mathbf{OH}}} \right)_{\mathbf{2}}}$तथा ${\mathbf{200}}{\text{ }}{\mathbf{g}}$जल को मिलाकर प्रतिहिम मिश्रण बनाया गया। विलयन की मोललता की गणना कीजिए। यदि विलयन का घनत्व ${\mathbf{1}}.{\mathbf{072}}{\text{ }}{\mathbf{g}}{\text{ }}{\mathbf{m}}{{\mathbf{L}}^{ - {\mathbf{1}}}}$हो तो विलयन की मोलरता निकालिए।

उत्तर: एथिलीन ग्लाइकॉल की मोललता 

$ = \dfrac{{222.6}}{{62 \times \dfrac{{200}}{{1000}}}}$

$ = 17.95{\text{ }}m$
विलयन का भार = ग्लाइकॉल का भार + जल का भार

$ = 222.6 + 200$

$ = 422.6{\text{ }}g$

विलयन का आयतन $ = \dfrac{{422.6}}{{1.072}}{\text{ }}mL$

एथिलीन ग्लाइकॉल की मोलरता 

$ = \dfrac{{222.6}}{{42 \times \dfrac{{422.6}}{{1.072 \times 1000}}}}$

$ = 9.11M$

9. एक पेय जल का नमूना क्लोरोफॉर्म $\left( {{\mathbf{CHC}}{{\mathbf{l}}_{\mathbf{3}}}} \right)$से कैंसरजन्य समझे जाने की सीमा तक बहुत अधिक संदूषित है। इसमें संदूषण की सीमा ${\mathbf{15}}{\text{ }}{\mathbf{ppm}}$(द्रव्यमान में) है –

(i) इसे द्रव्यमान प्रतिशत में व्यक्त कीजिए।

उत्तर: 

$15ppmCHC{l_3}$ का तात्पर्य है कि ${10^6}{\text{ }}g{H_2}O$में $15{\text{ }}gCHC{l_3}$ उपस्थित है।
(i) ∴ द्रव्यमान प्रतिशत 

$ = \dfrac{{15}}{{{{10}^6}}} \times 100$

$ = 1.5 \times {10^{ - 4}}$

(ii) जल के नमूने में क्लोरोफॉर्म की मोललता ज्ञात कीजिए।

उत्तर: मोललता $(m) = \dfrac{{15/119.5}}{{{{10}^6}}} \times 1000$

$ = 1.25 \times {10^{ - 4}}{\text{ }}m$

10. ऐल्कोहॉल एवं जल के एक विलयन में आण्विक अन्योन्यक्रिया की क्या भूमिका है?
उत्तर: ऐल्कोहॉल एवं जल के विलयन में ऐल्कोहॉल तथा जल के अणु अन्तराआण्विकH- बन्ध बनाते हैं। लेकिन यह ${H_2}O - {H_2}O$तथा ऐल्कोहॉल-ऐल्कोहॉल $H$-बन्ध से दुर्बल होते हैं। इससे अणुओं की वाष्प अवस्था में जाने की प्रवृत्ति बढ़ जाती है। अत: यह विलयन राउल्ट के नियम से धनात्मक विचलन प्रदर्शित करता है।

11. ताप बढ़ाने पर गैसों की द्रवों में विलेयता में हमेशा कमी आने की प्रवृत्ति क्यों होती है?

उत्तर: गैस + विलायक विलयन + ऊष्मा

गैस का द्रव में घुलना एक ऊष्माक्षेपी प्रक्रम है। ताप बढ़ाने पर साम्य बायीं ओर विस्थापित होता जाता है और विलयन से गैस मुक्त हो जाता है।

12. हेनरी का नियम तथा इसके कुछ महत्त्वपूर्ण अनुप्रयोग लिखिए।

उत्तर: हेनरी का नियम (Henry's Law) - सर्वप्रथम गैस की विलायक में विलेयता तथा दाब के मध्य मात्रात्मक सम्बन्ध हेनरी ने दिया। इसे हेनरी का नियम इसलिए कहते हैं। इसके अनुसार, "स्थिर ताप पर विलायक के प्रति एकांक आयतन में घुला गैस का द्रव्यमान विलयन के साथ साम्यावस्था में गैस के दाब के समानुपाती होता है। डाल्टन, जो हेनरी के समकालीन थे, उन्होंने भी स्वतन्त्र रूप से निष्कर्ष निकाला कि किसी द्रवीय विलयन में गैस की विलेयता गैस के आंशिक दाब पर निर्भर करती है। यदि हम विलयन में गैस के मोल-अंश को उसकी विलेयता का माप मानें तो यह कहा जा सकता है कि किसी विलयन में गैस का मोल-अंश उस विलयन के ऊपर उपस्थित गैस के आंशिक दाब के समानुपाती होता है।

अत: विकल्पतः हेनरी नियम को इस प्रकार व्यक्त किया जा सकता है -

"किसी गैस का वाष्प-अवस्था में आंशिक दाब $\left( p \right)$, उस विलयन में गैस के मोल-अंश (x) के समानुपाती होता है।"

$p{\text{ }}\alpha {\text{ }}x$

$p = {\text{ }}{K_H}.{\text{ }}x$

यहाँ ${K_H}$ हेनरी स्थिर है। जब एक से ज्यादा गैसों के मिश्रण को विलायक के सम्पर्क में लाया जाता है, तब प्रत्येक गैसीय अवयव अपने आंशिक दाब के समानुपात में घुलता है। इसीलिए हेनरी नियम अन्य गैसों की उपस्थिति से स्वतन्त्र होकर प्रत्येक गैस पर लागू किया जाता है।

हेनरी नियम के अनुप्रयोग (Applications of Henry's Law) - हेनरी नियम के उद्योगों में अनेक अनुप्रयोग हैं एवं यह कुछ जैविक घटनाओं को समझने में सहायक होता है। इसके कुछ महत्त्वपूर्ण अनुप्रयोग निम्नलिखित हैं -

1. सोडा-जल एवं शीतल पेयों में $C{O_2}$ की विलेयता बढ़ाने के लिए बोतल को अधिक दाब पर बन्द किया जाता है।

2. गहरे समुद्र में श्वास लेते हुए गोताखोरों को अधिक दाब पर गैसों को अधिक घुलनशीलता का सामना करना पड़ सकता है। अधिक बाहरी दाब के कारण श्वास के साथ ली गई वायुमण्डलीय गैसों की विलेयता रुधिर में अधिक हो जाती है। जब गोताखोर सतह की ओर आते हैं, बाहरी दाब धीरे-धीरे कम होने लगता है। इसके कारण घुली हुई गैसें बाहर निकलती हैं, इससे रुधिर में नाइट्रोजन के बुलबुले बन जाते हैं। यह केशिकाओं में अवरोध उत्पन्न कर देता है और एक चिकित्सीय अवस्था उत्पन्न कर देता है। जिसे बेंड्स (Bends) कहते हैं, यह बहुत पीड़ादायक एवं जानलेवा होता है। बेंड्स से तथा नाइट्रोजन की रुधिर में अधिक मात्रा के जहरीले प्रभाव से बचने के लिए, गोताखोरों द्वारा श्वास लेने के लिए उपयोग किए जाने वाले टैंकों में हीलियम मिलाकर तनु की गई वायु को भरा जाता है (इस वायु को संघटन इस प्रकार होता है$ - 11.7\% $ हीलियम, $56.2\% $ नाइट्रोजन तथा $32.1\% $ऑक्सीजन)।

3. अधिक ऊँचाई वाली जगहों पर ऑक्सीजन का आंशिक दाब सतही स्थानों से कम होता है, अत: इन जगहों पर रहने वाले लोगों एवं आरोहकों के रुधिर और ऊतकों में ऑक्सीजन की सान्द्रता निम्न हो जाती है। इसके कारण आरोहक कमजोर हो जाते हैं और स्पष्टतया सोच नहीं पाते। इन लक्षणों को एनॉक्सिया कहते हैं।
   
   

13. ${\mathbf{6}}.{\mathbf{56}}{\text{ }}{\mathbf{x}}{\text{ }}{\mathbf{1}}{{\mathbf{0}}^{ - {\mathbf{3}}}}{\mathbf{g}}$ एथेन युक्त एक संतृप्त विलयन में एथेन का आंशिक दाब ${\mathbf{1}}$ bar है। यदि विलयन में ${\mathbf{5}}.{\mathbf{00}}{\text{ }}{\mathbf{x}}{\text{ }}{\mathbf{1}}{{\mathbf{0}}^{ - {\mathbf{2}}}}{\mathbf{g}}$एथेन हो तो गैस का आंशिक दाब क्या होगा?

उत्तर: 

 $m{\text{ }} = {\text{ }}{K_H}x{\text{ }}p$
प्रथम मामले में, $6.56{\text{ }}x{\text{ }}{10^{ - 2}}g{\text{ }} = {\text{ }}{K_H}x{\text{ }}1{\text{ }}bar$
$KH{\text{ }} = {\text{ }}6.56{\text{ }}x{\text{ }}{10^{ - 2}}g{\text{ }}ba{r^{ - 2}}$
द्वितीय मामले में, $5.00{\text{ }}x{\text{ }}{10^{ - 2}}g{\text{ }} = {\text{ }}(6.56{\text{ }}x{\text{ }}{10^{ - 2}}g{\text{ }}ba{r^{ - 2}}){\text{ }}x{\text{ }}p$

या

$p = \dfrac{{5.00 \times {{10}^{ - 2}}g}}{{6.56 \times {{10}^{ - 2}}gba{r^{ - 1}}}}$

$ = 0.762bar$

14. राउल्ट के नियम से धनात्मक एवं ऋणात्मक विचलन का क्या अर्थ है तथा मिश्रण ${\mathbf{H}}$ का चिह्न इन विचलनों से कैसे सम्बन्धित है?

उत्तर: जब कोई विलयन सभी सान्द्रताओं पर राउल्ट के नियम का पालन नहीं करता तो वह अनादर्श विलयन (non-ideal solution) कहलाता है। इस प्रकार के विलयनों का वाष्प दाब राउल्ट के नियम द्वारा निर्धारित किए गए वाष्प दाब से या तो ज्यादा होता है या कम। यदि यह ज्यादा होता है तो यह विलयन राउल्ट के नियम से धनात्मक विचलन (positive deviation) प्रदर्शित करता है और यदि यह कम होता है तो यह ऋणात्मक विचलन (negative deviation) प्रदर्शित करता है।

(j) राउल्ट नियम से धनात्मक विचलन प्रदर्शित करने वाले अनादर्श विलयन (Non-ideal solutions showing positive deviation from Raoult's law) – दो अवयवो| $A$ तथा $B$ वाले एक द्विअंगी विलयन पर विचार करते हैं। यदि विलयन में $A - B$ अन्योन्यक्रियाएँ $A - A$ तथा $B - B$अन्योन्यक्रियाओं की तुलना में दुर्बल होती हैं अर्थात् विलेय विलायक अणुओं के मध्य अन्तराआण्विक आकर्षण बल विलेय-विलेय और विलायक-विलायक अणुओं की तुलना में दुर्बल होते हैं, तब इस प्रकार के विलयनों में से $A$ अथवा $B$ के अणु शुद्ध अवयव की तुलना में सरलता से पलायन कर सकते हैं। इसके परिणामस्वरूप विलयन के प्रत्येक अवयव का वाष्प दाब राउल्ट नियम के आधार पर अपेक्षित वाष्प दाब से अधिक होता है। इस प्रकार से कुल वाष्प दाब भी अधिक होता है। विलयन का यह व्यवहार राउल्ट नियम से धनात्मक विचलन के रूप में जाना जाता है। गणितीय रूप से इसे इस प्रकार व्यक्त कर सकते हैं।

${P_H} > {\text{ }}P{^\circ _A}{^X_A}$ तथा ${P_B} > {\text{ }}P{^\circ _B}{^X_B}$ इसी प्रकार कुल वाष्प दाब, $p{\text{ }} = {\text{ }}{p_A} + {\text{ }}{p_B}$ सदैव $(p{^\circ _A}{^X_A} + {\text{ }}p{^\circ _B}{^X_B})$ से अधिक होता है।

इस प्रकार के विलयनों में, मिश्रण $H$ शून्य नहीं होता, अपितु धनात्मक होता है क्योकि $A - A$अथवा $B - B$आकर्षण बलों के विरुद्ध ऊष्मा की आवश्यकता होती है। अत: घुलनशीलता ऊष्माशोषी प्रक्रिया होती है।

(ii) राउल्ट नियम से ऋणात्मक विचलन प्रदर्शित करने वाले अनादर्श विलयन (Non-ideal solutions showing negative deviation from Raoult's law) - इस प्रकार के विलयनों में $A - A$ व $B - B$ के बीच अन्तराआण्विक आकर्षण बल $A - B$ की तुलना में दुर्बल होता है, अत: इस प्रकार के विलयनों में $A$ तथा $B$ अणुओं की पलायन प्रवृत्ति शुद्ध अवयव की तुलना में कम होती है, परिणामस्वरूप विलयन के हर एक अवयव का वाष्प दाब राउल्ट नियम के आधार पर अपेक्षित वाष्प दाब से कम होता है। इसी प्रकार कुल वाष्प दाब भी कम होता है। गणितीय रूप में,

${P_A} < P{x_A}\;$ तथा  ${P_B} < {P^0}_B{x_B}\left( {{P_A} + {P_B}} \right) < \left( {{P^0}_A{x_A} + {P^0}_B{x_B}} \right)$

इस प्रकार के विलयनों में मिश्रण $H$ शून्य नहीं होता, अपितु ऋणात्मक होता है क्योंकि आकर्षण बलों में वृद्धि से ऊर्जा उत्सर्जित होती है। अत: घुलनशीलता ऊष्माक्षेपी प्रक्रिया उत्पन्न होती है।

15. विलायक के सामान्य क्वथनांक पर एक अवाष्पशील विलेय के ${\mathbf{2}}\% $ जलीय विलयन का ${\mathbf{1}}.{\mathbf{004}}{\text{ }}{\mathbf{bar}}$ वाष्प दाब है। विलेय का मोलर द्रव्यमान क्या है?
उत्तर: क्वथनांक पर शुद्ध जल का वाष्प दाब $\left( {p^\circ } \right){\text{ }} = {\text{ }}1{\text{ }}atm{\text{ }} = {\text{ }}1.013{\text{ }}bar$

विलयन का वाष्प दाब $({p_S}){\text{ }} = {\text{ }}1.004{\text{ }}bar$

लेय का द्रव्यमान $({w_2}){\text{ }} = {\text{ }}2{\text{ }}g$
विलयन का द्रव्यमान $ = {\text{ }}100{\text{ }}g$

विलयन का द्रव्यमान $ = {\text{ }}98{\text{ }}g$
तनु विलयनों के लिए राउल्ट के नियमानुसार,

$\dfrac{{{p^o} - {p_s}}}{p}p\;{\text{ }} = \dfrac{{{n_2}}}{{n1 + n2}} = {n_2}{n_1}$

$ = \dfrac{{\dfrac{{{n_2}}}{{{n_2}}}}}{{\dfrac{{{n_1}}}{{{n_1}}}}} = \dfrac{n}{{{n_2}}} \times \dfrac{{{n_1}}}{n}\dfrac{{\left( {1.013 - 1.004} \right)}}{{1.013bar}}\;$

$ = \dfrac{{2{\text{ }}g}}{{{M_2}}} \times \dfrac{{18{\text{ }}g{\text{ }}mo{l^{ - 1}}}}{{98{\text{ }}g}}M2\;$

$ = \dfrac{{2 \times 18}}{{98}} \times \dfrac{{1.013}}{{0.009}}{\text{ }}g{\text{ }}mo{l^{ - 1}}$

$ = 41.35{\text{ }}g{\text{ }}mo{l^{ - 1}}$

16. हेप्टेन एवं ऑक्टेन एक आदर्श विलयन बनाते हैं। ${\mathbf{373}}{\text{ }}{\mathbf{K}}$ पर दोनों द्रव घटकों के वाष्प दाब क्रमशः ${\mathbf{105}}.{\mathbf{2}}{\text{ }}{\mathbf{k}}{\text{ }}{\mathbf{Pa}}$ तथा ${\mathbf{46}}.{\mathbf{8}}{\text{ }}{\mathbf{k}}{\text{ }}{\mathbf{Pa}}$ हैं। ${\mathbf{26}}.{\mathbf{0}}{\text{ }}{\mathbf{g}}$ हेप्टेन एवं ${\mathbf{35}}.{\mathbf{0}}{\text{ }}{\mathbf{g}}$ ऑक्टेन के मिश्रण का वाष्प दाब क्या होगा?

उत्तर:

$P = {P^o}$ हेंटेनेन$ + P$ऑक्टेन$ = P$हेप्टेन $\dfrac{n}{{n + N}} + {P^o}$ऑक्टेन$\dfrac{n}{{n + N}}$

 $ = 105.2 \times \dfrac{{\dfrac{{26}}{{100}}}}{{\dfrac{{26}}{{100}} + \dfrac{{35}}{{114}}}} + 46.8 \times \dfrac{{\dfrac{{35}}{{114}}}}{{\dfrac{{26}}{{100}} + \dfrac{{35}}{{114}}}}$

$ = 73.08kPa$

17. ${\mathbf{300}}{\text{ }}{\mathbf{K}}$ पर जल का वाष्प दाब ${\mathbf{12}}.{\mathbf{3}}{\text{ }}{\mathbf{k}}{\text{ }}{\mathbf{Pa}}$है। इसमें बने अवाष्पशील विलेय के एक मोलल विलयन का वाष्प दाब ज्ञात कीजिए।

उत्तर: एक मोलल विलयन का तात्पर्य है कि $1{\text{ }}kg$ विलायक (जल) में विलेय का $1{\text{ }}mol$उपस्थित है।

विलेय का मोल प्रभाज 

$ = \dfrac{1}{{1 + 55.5}}$

$ = 0.0177$

अत:

$\dfrac{{{p^o} - {p_s}}}{p}\; = {x_2}\;$अर्थात् $\dfrac{{12.3 - {p_s}}}{{12.3}}$

$ = 0.0177{p_s}\;$

$ = 12.08kPa\;\;$

18. $114{\text{ }}g$ ऑक्टेन में किसी अवाष्पशील विलेय (मोलर द्रव्यमान $40{\text{ }}gmo{l^{ - 1}}$) की कितनी मात्रा घोली जाए कि ऑक्टेन का वाष्प दाब घट कर मूल वाष्प दाब का $80\% $ रह जाए?

उत्तर: 

प्रश्नानुसार,${M_2} = 40$,${w_1} = 114{\text{ }}g$

∵  $\dfrac{{{p^o} - s}}{{{p^o}}} = \dfrac{{{w_2}{M_1}}}{{{w_1}{M_2}}}$ या $\dfrac{{100 - 80}}{{100}}$

$ = \dfrac{{{w_2} \times 114}}{{114 \times 40}}$  या ${w_2} = 8g$

19. एक विलयन जिसे एक अवाष्पशील ठोस के ${\mathbf{30}}{\text{ }}{\mathbf{g}}$ को ${\mathbf{90}}{\text{ }}{\mathbf{g}}$ जल में विलीन करके बनाया गया है। उसका ${\mathbf{298}}{\text{ }}{\mathbf{K}}$ पर वाष्प दाब ${\mathbf{2}}.{\mathbf{8}}{\text{ }}{\mathbf{k}}{\text{ }}{\mathbf{Pa}}$ है। विलयन में ${\mathbf{18}}{\text{ }}{\mathbf{g}}$ जल और मिलाया जाता है जिससे नया वाष्प दाब ${\mathbf{298}}{\text{ }}{\mathbf{K}}$ पर ${\mathbf{2}}.{\mathbf{9}}{\text{ }}{\mathbf{k}}{\text{ }}{\mathbf{Pa}}$ हो जाता है। निम्नलिखित की गणना कीजिए-

(i) विलेय का मोलर द्रव्यमान

(ii) ${\mathbf{298}}{\text{ }}{\mathbf{K}}$ पर जल का वाष्प दाब।

उत्तर:

$\dfrac{{{p^o} - s}}{{{p^o}}} = \dfrac{{{w_2}{M_1}}}{{{w_1}{M_2}}}$

I मामले में,
$\dfrac{{{p^o} - 2.8}}{{2.8}} = \dfrac{{30 \times 18}}{{90 \times 90}}$

$ = \dfrac{6}{{{M_2}}}\dfrac{{p - 2.9}}{{2.9}} = \dfrac{{30 \times 18}}{{108 \times {M_2}}} = \dfrac{5}{{{M_2}}}$ ...(i)
समीकरण (i) तथा (ii) से, ${p^o} = 3.5kPa$,${M_2} = 23gmo{l^{ - 1}}$

20. शक्कर के ${\mathbf{5}}\% $(द्रव्यमान) जलीय विलयन का हिमांक ${\mathbf{271}}{\text{ }}{\mathbf{K}}$ है। यदि शुद्ध जल को हिमांक ${\mathbf{273}}.{\mathbf{15}}{\text{ }}{\mathbf{K}}$ है तो ग्लूकोस के ${\mathbf{5}}\% $ जलीय विलयन के हिमांक की गणना कीजिए।

उत्तर:

$\vartriangle {T_f} = \dfrac{{1000 \times {K_f} \times {w_2}}}{{{m_2} \times m}}$
अतः

${w_2} = 5{\text{ }}g$,$w = 100 - 5 = 95{\text{ }}g$,

$\Delta {T_f} = 273.15 - 271$
$ = 2.15$,

${M_2} = 342$ (शर्करा)
$\therefore 2.15 = \dfrac{{1000 \times {K_f} \times 5}}{{342 \times 95}}$
ग्लूकोस के लिए, $\vartriangle {T_f} = \dfrac{{1000 \times {K_f} \times 5}}{{180 \times 95}}$
समीकरण (i) तथा (ii) से, ${T_f} = 4.085{\text{ }}K$हिमांक 

$ = 273.15 - 4.09$

$ = 269.06$

21. दो तत्व ${\mathbf{A}}$ एवं ${\mathbf{B}}$ मिलकर ${\mathbf{AB2}}$ एवं ${\mathbf{AB4}}$ सूत्र वाले दो यौगिक बनाते हैं। ${\mathbf{20}}{\text{ }}{\mathbf{g}}$बेन्जीन में घोलने पर ${\mathbf{1g}}{\text{ }}{\mathbf{AB2}}$हिमांक को ${\mathbf{2}}.{\mathbf{3}}{\text{ }}{\mathbf{K}}$अवनमित करता है, जबकि ${\mathbf{1}}.{\mathbf{0}}{\text{ }}{\mathbf{g}}$ ${\mathbf{AB4}}$ से ${\mathbf{1}}.{\mathbf{3}}{\text{ }}{\mathbf{K}}$का अवनमन होता है। बेन्जीन के लिए मोलर अवनमन स्थिरांक ${\mathbf{5}}.{\mathbf{1}}{\text{ }}{\mathbf{K}}{\text{ }}{\mathbf{kg}}{\text{ }}{\mathbf{mo}}{{\mathbf{l}}^{ - {\mathbf{1}}}}$ है। ${\mathbf{A}}$  एवं ${\mathbf{B}}$ के परमाण्वीय द्रव्यमान की गणना कीजिए।
उत्तर:

$AB$ के लिए : अणु द्रव्यमान $ = a + 2b$( $a$ तथा $b$ तत्त्व $A$ और $B$ के परमाणु भार हैं) $AB4$ के लिए : अणु द्रव्यमान $ = a + 4b$
सूत्र

$\vartriangle {T_f} = \dfrac{{1000 \times {K_f} \times w}}{{{m_2} \times w}}$

$AB2$ के लिए,

$2.3 = \dfrac{{1000 \times 5.1 \times 1}}{{(a + 2b) \times 20}}$

$a + 2b\; = 110.871.3\; = \dfrac{{1000 \times 5.1 \times 1}}{{(a + 4b) \times 20}}$

समीकरण (i) तथा (ii) को हल करने पर

$a = 25.59u,b = 42.64u$

22. ${\mathbf{300}}{\text{ }}{\mathbf{K}}$ पर ${\mathbf{36}}{\text{ }}{\mathbf{g}}$ प्रति लीटर सान्द्रता वाले ग्लूकोस के विलयन का परासरण दाब ${\mathbf{4}}.{\mathbf{98}}{\text{ }}{\mathbf{bar}}$ है। यदि इसी ताप पर विलयन का परासरण दाब ${\mathbf{1}}.{\mathbf{52}}{\text{ }}{\mathbf{bar}}$हो तो उसकी सान्द्रता क्या होगी?
उत्तर:
प्रश्नानुसार, परासरण दाब $ = {\text{ }}4.98{\text{ }}bar$, $w{\text{ }} = {\text{ }}36{\text{ }}g$, $V{\text{ }} = {\text{ }}1{\text{ }}L$(I मामले में)
परासरण दाब $ = {\text{ }}1.52{\text{ }}bar$ (II मामले में)
I के लिए, $\pi V{\text{ }} = {\text{ }}\dfrac{w}{{MRT}}$
$4.98{\text{ }} \times {\text{ }}1{\text{ }} = {\text{ }}\dfrac{{36}}{{180{\text{ }} \times {\text{ }}R{\text{ }} \times {\text{ }}T}}$
II के लिए, $1.52{\text{ }} = {\text{ }}c{\text{ }}x{\text{ }}R{\text{ }}x{\text{ }}T(c{\text{ }}\; = \dfrac{w}{{M \times V}})$                

समीकरण (i) तथा (ii) को हल करने पर, $c = {\text{ }}0.061{\text{ }}mol{\text{ }}{L^{ - 1}}$

23. निम्नलिखित युग्मों में उपस्थित सबसे महत्त्वपूर्ण अन्तरआण्विक आकर्षण बलों का सुझाव दीजिए –

1. ${\mathbf{n}} - $हेक्सेन व ${\mathbf{n}} - $ऑक्टेन

उत्तर: लण्डन परिक्षेपण बल

2. ${{\mathbf{I}}_{\mathbf{2}}}$ तथा ${\mathbf{CC}}{{\mathbf{l}}_{\mathbf{4}}}$

उत्तर: लण्डन परिक्षेपण बल

3. ${\mathbf{NaCl}}{{\mathbf{O}}_{\mathbf{4}}}$ तथा ${{\mathbf{H}}_{\mathbf{2}}}{\mathbf{O}}$

उत्तर: आयन-द्विध्रुव अन्योन्यक्रियाएँ

4.मेथेनॉल तथा ऐसीटोन

उत्तर: द्विध्रुव-द्विध्रुव अन्योन्यक्रियाएँ

5.ऐसीटोनाइट्राइल $\left( {{\mathbf{C}}{{\mathbf{H}}_{\mathbf{3}}}{\mathbf{CN}}} \right)$ तथा ऐसीटोन $({{\mathbf{C}}_{\mathbf{3}}}{{\mathbf{H}}_{_{\mathbf{6}}}}{\mathbf{O}})$।

उत्तर: द्विध्रुव–द्विध्रुव अन्योन्यक्रियाएँ

24. विलेय-विलायक आकर्षण के आधार पर निम्नलिखित को n-ऑक्टेन में विलेयता के बढ़ते क्रम में व्यवस्थित कीजिए $--{\mathbf{KCl}},{\text{ }}{\mathbf{C}}{{\mathbf{H}}_{\mathbf{3}}}{\mathbf{OH}},{\text{ }}{\mathbf{C}}{{\mathbf{H}}_{\mathbf{3}}}{\mathbf{CN}}$, साइक्लोहेक्सेन।
उत्तर:
$KCl{\text{ }} < {\text{ }}C{H_3}OH{\text{ }} < {\text{ }}C{H_3}CN{\text{ }} < $ साइक्लोहेक्सेन
$KCl$ आयनिक यौगिक,है। अत: यह अध्रुवीय विलायक में घुलता नही है , अत: यह 2-ऑक्टेन में सबसे कम विलेय है। साइक्लोहेक्सेन अध्रुवीय होने के कारण n-ऑक्टेन में आसानी से विलेय होती है। $C{H_3}CN,{\text{ }}C{H_3}OH$ की तुलना में कम ध्रुवीय है, अत: इसकी विलेयता $C{H_3}OH$ से अधिक होती है।

25. पहचानिए कि निम्नलिखित यौगिकों में से कौन-से जल में अत्यधिक विलेय, आंशिक रूप से विलेय तथा अविलेय हैं –

1. फीनॉल

उत्तर: आंशिक विलेय

2. टॉलूईन

उत्तर: अविलेय

3. फॉर्मिक अम्ल

उत्तर: अत्यधिक विलेय

4. एथिलीन ग्लाइकॉल

उत्तर: अत्यधिक विलेय

5. क्लोरोफॉर्म

उत्तर: अविलेय

6. पेन्टेनॉल।

उत्तर: आंशिक विलेय

26. यदि किसी झील के जल का घनत्व ${\mathbf{1}}.{\mathbf{25}}{\text{ }}{\mathbf{g}}{\text{ }}{\mathbf{m}}{{\mathbf{L}}^{ - {\mathbf{1}}}}$ है तथा उसमें ${\mathbf{92}}{\text{ }}{\mathbf{g}}{\text{ }}{\mathbf{Na}} + $आयन प्रति किलो जल में उपस्थित हैं तो झील में ${\mathbf{Na}} + $आयन की मोललता ज्ञात कीजिए।
उत्तर:
विलेय का भार $ = {\text{ }}92{\text{ }}g$, 

विलायक का भार $ = {\text{ }}1000{\text{ }}g$

$m\; = \;$ विलेय का भार / अणुभार $ \times 1000$ विलायक का भार    

$ = \dfrac{{92}}{{23}} \times \dfrac{{1000}}{{1000}}$

$ = 4{\text{ }}m\;$

27. अगर ${\mathbf{CuS}}$ का विलेयता गुणनफल ${\mathbf{6}}{\text{ }}{\mathbf{x}}{\text{ }}{\mathbf{1}}{{\mathbf{0}}^{ - {\mathbf{16}}}}$ है तो जलीय विलयन में उसकी अधिकतम मोलरता ज्ञात कीजिए।

उत्तर:

जलीय विलयन में $CuS$ की अधिकतम मोलरता $ = {\text{ }}mol{\text{ }}{L^{ - 1}}$ में CuS की विलेयता यदि $ = {\text{ }}mol{\text{ }}{L^{ - 1}}$ में $CuS$ की विलेयता s है 

$CuS \rightleftharpoons C{u^{2 + }} + {S^{2 - }}{K_{sp}} = \left[ {C{u^{2 + }}} \right]\left[ {{S^{2 - 5}}} \right] = s \times s = {s^2}$

${s^2} = 6 \times {10^{ - 16}}{\text{ }}$या  

$s = \sqrt {6 \times {{10}^{ - 16}}} \;\;$

$ = 2.45 \times {10^{ - 8}}{\text{ }}mol{\text{ }}{L^{ - 1}}$ तो

28. जब ${\mathbf{6}}.{\mathbf{5}}{\text{ }}{\mathbf{g}}$ ऐस्पिरीन $({{\mathbf{C}}_{\mathbf{9}}}{{\mathbf{H}}_{\mathbf{8}}}{{\mathbf{O}}_{\mathbf{4}}})$ को ${\mathbf{450}}{\text{ }}{\mathbf{g}}$ ऐसीटोनाइट्राइल $({\mathbf{C}}{{\mathbf{H}}_{\mathbf{3}}}{\mathbf{CN}})$ में घोला जाए तो ऐस्पिरीन का ऐसीटोनाइट्राइल में भार प्रतिशत ज्ञात कीजिए।

उत्तर: 

ऐस्पिरीन का द्रव्यमान प्रतिशत

= ऐस्पिरीन का द्रव्यमान    ऐस्पिरीन का द्रव्यमान + ऐसीटोनाइट्राइल का द्रव्यमान $ \times 100$

$ = \dfrac{{6.5}}{{6.5 + 450}} \times 100$

$ = 1.424\% $

29. नैलॉन $({{\mathbf{C}}_{{\mathbf{19}}}}{{\mathbf{H}}_{{\mathbf{21}}}}{\mathbf{N}}{{\mathbf{O}}_{\mathbf{3}}})$जो कि मॉर्फीन जैसी होती है, का उपयोग स्वापक उपभोक्ताओं द्वारा स्वापक छोड़ने से उत्पन्न लक्षणों को दूर करने में किया जाता है। सामान्यतया नैलॉन की ${\mathbf{1}}.{\mathbf{5}}{\text{ }}{\mathbf{mg}}$ खुराक दी जाती है। उपर्युक्त खुराक के लिए ${\mathbf{1}}.{\mathbf{5}}{\text{ }}{\mathbf{x}}{\text{ }}{\mathbf{1}}{{\mathbf{0}}^{ - {\mathbf{3}}}}{\text{ }}{\mathbf{m}}$ जलीय विलयन का कितना द्रव्यमान आवश्यक होगा?

उत्तर:

विलेय का भार $ = {\text{ }}1.5{\text{ }}mg$

$ = {\text{ }}0.0015{\text{ }}g,$

विलेय का अणुभार $ = {\text{ }}311,$

विलायक को भार $ = {\text{ }}w$

m  = विलेय का भार / विलेय का अणुभार $ \times \dfrac{{1000}}{w}1.5 \times {10^{ - 3}}$

 $ = \dfrac{{0.0015}}{{311}} \times \dfrac{{1000}}{w}$

$w\; = \dfrac{{0.0015}}{{311}} \times \dfrac{{1000}}{{1.5 \times {{10}^{ - 3}}}}$

$ = 3.2154$

विलायक का भार $ = {\text{ }}3.2154{\text{ }}g$,

विलयन का भार 

$ = {\text{ }}3.2154{\text{ }} + {\text{ }}0.0015$

$ = {\text{ }}3.2159{\text{ }}g$

30. बेन्जोइक अम्ल का मेथेनॉल में ${\mathbf{0}}.{\mathbf{15}}{\text{ }}{\mathbf{m}}$ विलयन बनाने के लिए आवश्यक मात्रा की गणना कीजिए।

उत्तर:

$V = 250{\text{ }}ml$, $m{\text{ }} = {\text{ }}0.15{\text{ }}m$, विलेय का अणुभार $ = {\text{ }}122$, विलेय की मात्रा $ = {\text{ }}?$

$m\; = \;$विलेय का भार / विलेय का अणुभार $ \times 1000$ / विलयन का आयतन mL में  

$0.15 = \dfrac{w}{{122}} \times \dfrac{{1000}}{{250}}$

$w\; = \dfrac{{0.15 \times 122 \times 250}}{{1000}}$

$ = 4.575g\;$

31. ऐसीटिक अम्ल, ट्राइक्लोरोऐसीटिक अम्ल एवं ट्राइफ्लुओरो ऐसीटिक अम्ल की समान मात्रा से जल के हिमांक में अवनमन इनके उपर्युक्त दिए गए क्रम में बढ़ता है। संक्षेप में समझाइए।

उत्तर: 

हिमांक में अवनमन निम्न क्रम इस प्रकार होता है –

ऐसीटिक अम्ल $ < $ ट्राइक्लोरोऐसीटिक अम्ल $ < $ ट्राइफ्लुओरोऐसीटिक अम्लफ्लोरीन अधिक ऋणविद्युती होने के कारण उच्चतम इलेक्ट्रॉन निष्कासन प्रेरणिक पर प्रभाव डालता है। अतः ट्राइफ्लुओरोऐसीटिक अम्ल प्रबल अम्ल है जबकि ऐसीटिक अम्ल दुर्बलतम अम्ल है।। अतः ट्राइफ्लुओरोऐसीटिक अम्ल अत्यधिक आयनित होकर अधिक आयन उत्पन्न करता है जबकि ऐसीटिक अम्ल सबसे कम आयन उत्पन्न करता है। अधिक आर्यन उत्पन्न करने के कारण ट्राइफ्लुओरोऐसीटिक अम्ल हिमांक में अधिक अवनमन करता है एवं ऐसीटिक अम्ल सबसे कम।

32. ${\mathbf{C}}{{\mathbf{H}}_{\mathbf{3}}}--{\text{ }}{\mathbf{C}}{{\mathbf{H}}_{\mathbf{2}}}--{\text{ }}{\mathbf{CHCl}}{\text{ }}--{\text{ }}{\mathbf{COOH}}$ के ${\mathbf{10}}{\text{ }}{\mathbf{g}}$ को ${\mathbf{250}}{\text{ }}{\mathbf{g}}$ जल में मिलाने से होने वाले हिमांक का अवनमन परिकलित कीजिए। $({{\mathbf{K}}_{\mathbf{a}}} = {\text{ }}{\mathbf{1}}.{\mathbf{4}}{\text{ }} \times {\text{ }}{\mathbf{1}}{{\mathbf{0}}^{ - {\mathbf{3}}}},{\text{ }}{{\mathbf{K}}_{\mathbf{f}}} = {\text{ }}{\mathbf{186}}{\text{ }}{\mathbf{K}}{\text{ }}{\mathbf{kg}}{\text{ }}{\mathbf{mo}}{{\mathbf{l}}^{ - {\mathbf{1}}}})$

उत्तर:

$C{H_3}C{H_2}CHClCOOH$ का मोलर द्रव्यमान $ = 122.5gmo{l^{ - 1}}$

$10gC{H_3}C{H_{_2}}CHClCOOH = \dfrac{{10}}{{122.5}}mol$

$ = 8.16 \times {10^{ - 2}}mol$

विलयन की मोललता $m = \dfrac{{8.16 \times {{10}^{ - 2}}}}{{250}} \times 1000$

$ = 0.3264$ यदि $C{H_3}C{H_2}CHClCOOH$ की वियोजन की मात्रा $a$  हो तब

वांट-हॉफ गुणांक की गणना

$C{H_3}C{H_2}CHClCOOH \to C{H_3}C{H_2}CHClCO{O^ - } + {H^ + }$प्रारम्भिक मोल   साम्य पर मोल $1$  कुल $ = 1 + a\;i = \dfrac{{1 + a}}{1} = 1 + a = 1 + 0.065 = 1.065\;$

${T_f} = iKfm = 1.065 \times 1.86 \times 0.3264\;$

$ = 0.649 \approx 0.65\;$

33. ${\mathbf{C}}{{\mathbf{H}}_{\mathbf{2}}}{\mathbf{FCOOH}}$के ${\mathbf{19}}.{\mathbf{5}}{\text{ }}{\mathbf{g}}$ को ${\mathbf{500}}{\text{ }}{\mathbf{g}}{\text{ }}{\mathbf{H2O}}$में घोलने पर जल के हिमांक में ${\mathbf{10}}^\circ {\mathbf{C}}$का अवनमन देखा गया। फ्लुओरोऐसीटिक अम्ल का वान्ट हॉफ गुणक तथा वियोजन स्थिरांक परिकलित कीजिए।

उत्तर: 

प्रश्नानुसार,${w_2} = 19.5g$,${w_1} = 500g$, ${K_f} = 1.86Kkgmo{l^{ - 1}}$,$\left( {\vartriangle {T_f}} \right)$  प्रेक्षित $ = {1.0^o}$

${M_2}$( प्रेक्षित) 

$ = \dfrac{{1000 \times {K_f} \times {w_2}}}{{{w_1} \times \Delta {T_f}}}$

$ = \dfrac{{1000 \times 1.86 \times 19.5}}{{500 \times 1.0}}$

$ = 72.54gmo{l^{ - 1}}$
$C{H_2}FCOOH$ के लिए $M_2$ (परिकलित) 

$ = 14 + 19 + 45$

$ = 78gmo{l^{ - 1}}$

वांट-हॉफ गुणांक 

(i)v

$ = \dfrac{{78}}{{72.54}}$

$ = 10753$
माना वियोजन की मात्रा  है तो
प्रारम्भ में,

$C{H_2}FCOOH\; \to C{H_2}FCO{O^ - } + {H^ + }C\;mol\;{L^{ - 1}}$ $00C\left( {1 - a} \right)CaCa$

$\therefore {\text{ }}i = \dfrac{{C\left( {1 + a} \right)}}{C} = 1 + \;\alpha $ या 

$\alpha  = i - 1 = 1.0753 - 1 = 0.0753\;\;$

${K_a} = \dfrac{{\left[ {C{H_2}FCO{O^ - }} \right]\left[ {{H^ + }} \right]}}{{\left[ {C{H_2}FCOOH} \right]}}$

$ = \dfrac{{Ca.Ca}}{{C\left( {1 - a} \right)}}$$ = \dfrac{{C{a^2}}}{{1 - a}}\;$लेकिन  

$C = \dfrac{{19.5}}{{78}} \times \dfrac{1}{{500}} \times 1000$

$ = 0.5M$

$\therefore {\text{ }}Ka = \dfrac{{C{a^2}}}{{1 - a}}$

$ = \dfrac{{\left( {0.5} \right){{\left( {0.0753} \right)}^2}}}{{1 - 0.0753}}$

$ = 3.07 \times {10^{ - 3}}$

34. 293 K पर जल का वाष्प दाब 17.535 mm Hg है। यदि 25 g ग्लूकोस को 450 g जल में घोलें तो 293 K पर जल का वाष्प दाब परिकलित कीजिए।

उत्तर: जल के मोलों की संख्या $\left( {{n_1}} \right) = \dfrac{{450}}{{18}} = 25$
ग्लूकोस के मोलों की संख्या $\left( {{n_2}} \right) = \dfrac{{25}}{{180}} = 0.138$

वाष्प दाब्ध में अवनमन $ = \dfrac{{{p^o} - {p_s}}}{{{p^o}}} = \dfrac{{{n_2}}}{{n + n}}$
या  $17.535 - {p_s}^o = \dfrac{{0.138 \times 17.535}}{{25 + 0.138}}\;$

या   ${p_s} = 17.44mmHg$

35. ${\mathbf{298}}{\text{ }}{\mathbf{K}}$ पर मेथेन की बेन्जीन में मोललता का हेनरी स्थिरांक ${\mathbf{4}}.{\mathbf{27}}{\text{ }}{\mathbf{x}}{\text{ }}{\mathbf{105}}{\text{ }}{\mathbf{mm}}{\text{ }}{\mathbf{Hg}}$ है। ${\mathbf{298}}{\text{ }}{\mathbf{K}}$  तथा ${\mathbf{760}}{\text{ }}{\mathbf{mm}}{\text{ }}{\mathbf{Hg}}$ दाब पर मेथेन की बेन्जीन में विलेयता परिकलित कीजिए।

उत्तर: 

हेनरी के नियमानुसार,

${p_A} = {K_H}{x_A}\;$ या  ${x_A} = \dfrac{{{p_A}}}{{{K_H}}}{p_A}$

$ = 760mmHg$,

${K_H} = 4.27 \times {10^5}mmHg$

${p_A} = \dfrac{{760}}{{4.27 \times {{10}^5}}}$

$ = 1.78 \times {10^{ - 3}}$

36. ${\mathbf{100}}{\text{ }}{\mathbf{g}}$ द्रव ${\mathbf{A}}$ (मोलर द्रव्यमान ${\mathbf{140}}{\text{ }}{\mathbf{g}}{\text{ }}{\mathbf{mo}}{{\mathbf{l}}^{ - {\mathbf{1}}}}$) को ${\mathbf{1000}}{\text{ }}{\mathbf{g}}$ द्रव ${\mathbf{B}}$ (मोलर द्रव्यमान ${\mathbf{180}}{\text{ }}{\mathbf{g}}{\text{ }}{\mathbf{mo}}{{\mathbf{l}}^{ - {\mathbf{1}}}}$) में घोला गया। शुद्ध द्रव ${\mathbf{B}}$ का वाष्प दाब ${\mathbf{500}}{\text{ }}{\mathbf{Torr}}$ पाया गया। शुद्ध द्रव ${\mathbf{A}}$ का वाष्प दाब तथा विलयन में उसका वाष्प दाब परिकलित कीजिए यदि विलयन का कुल वाष्प दाब ${\mathbf{475}}{\text{ }}{\mathbf{Torr}}$ हो।
उत्तर: ${\mathbf{300}}{\text{ }}{\mathbf{K}}$
${p_B} = {x_B}{p^o}_B$

$ = 500 \times 0.8860$

$ = 443$

विलयन का वाष्प दाब $475$ है। अतः विलयन में,
$A$ का वाष्प   दाब 

$ = 475 - 443$ 

$ = 32\;torr\;\;$

$\therefore \;{p_A} = {p^o}_A \times {x_A}$  या   

$32 = {p^o}_A \times 0.1139$ या  

${p^o}_A = \dfrac{{32}}{{0.1139}}$

$ = 280.94\;torr\;$

37. ${\mathbf{328}}{\text{ }}{\mathbf{K}}$ पर शुद्ध ऐसीटोन एवं क्लोरोफॉर्म के वाष्प दाब क्रमशः ${\mathbf{741}}.{\mathbf{8}}{\text{ }}{\mathbf{mm}}{\text{ }}{\mathbf{Hg}}$ तथा ${\mathbf{632}}.{\mathbf{8}}{\text{ }}{\mathbf{mm}}{\text{ }}{\mathbf{Hg}}$ हैं। यह मानते हुए कि संघटन के सम्पूर्ण परास में ये आदर्श विलयन बनाते हैं, ${\mathbf{P}}$ कल , ${\mathbf{P}}$ क्लोरोफॉर्म तथा Pएसीटोन  को $x$एसीटोन  के फलन के रूप में आलेखित कीजिए। मिश्रण के विभिन्न संघटनों के प्रेक्षित प्रायोगिक आँकड़े अग्रलिखित हैं –

उपर्युक्त आँकड़ों को भी उसी ग्राफ में आलेखित कीजिए और इंगित कीजिए कि क्या इसमें आदर्श विलयन से धनात्मक अथवा ऋणात्मक विचलन है?

उत्तर:
वायु के जल के साथ साम्य पर कुल दाब $ = 10atm.$

∵ वायु में $20\% $ ऑक्सीजन तथा $79\% $  नाइट्रोजन आयतनानुसार उपस्थित हैं।

उपर्युक्त आँकड़ों के आधार पर ग्राफ की प्रकृति निम्नलिखित निचे दी गयी है –

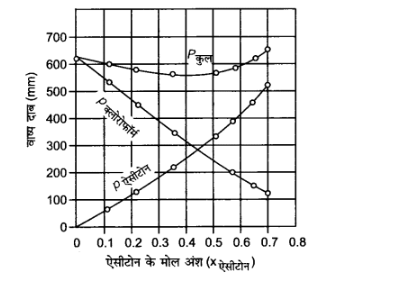
चूंकि $p$ कल का ग्राफ नीचे की ओर झुका है, अत: विलयन राउल्ट के नियम से ऋणात्मक विचलन प्रदर्शित कर रहा है।

38.संघटनों के सम्पूर्ण परास में बेन्जीन तथा टॉलूईन आदर्श विलयन बनाते हैं। ${\mathbf{300}}{\text{ }}{\mathbf{K}}$ पर शुद्ध बेन्जीन तथा टॉलूईन का वाष्प दाब क्रमशः ${\mathbf{50}}.{\mathbf{71}}{\text{ }}{\mathbf{mm}}{\text{ }}{\mathbf{Hg}}$ तथा ${\mathbf{32}}.{\mathbf{06}}{\text{ }}{\mathbf{mm}}{\text{ }}{\mathbf{Hg}}$है। यदि ${\mathbf{80}}{\text{ }}{\mathbf{g}}$ बेन्जीन को ${\mathbf{100}}{\text{ }}{\mathbf{g}}$ टॉलूईन में मिलाया जाए तो वाष्प अवस्था में उपस्थित बेन्जीन के मोल-अंश परिकलित कीजिए।
उत्तर:
द्रव अवस्था में ${n_B} = {\text{ }}\dfrac{{80}}{{78}}$

$= {\text{ }}1.026$,

${n_T} = {\text{ }}\dfrac{{100}}{{92}}$

$= {\text{ }}1.087$

${X_B} = {\text{ }}0.486,{\text{ }}{X_T} = {\text{ }}0.514$
${P_B} = {\text{ }}50.71 \times 0.486$

$ = {\text{ }}24.65$
${p_T} = {\text{ }}32.06 \times 0.514$

$ = {\text{ }}16.48$
बेंजीन का वाष्प अवस्था में मोल प्रभाज 

$= \dfrac{{24.65}}{{24.65 + 16.48}}$

$= 0.60$

39. वायु अनेक गैसों का मिश्रण है। ${\mathbf{298}}{\text{ }}{\mathbf{K}}$ पर आयतन में मुख्य घटक ऑक्सीजन और नाइट्रोजन लगभग ${\mathbf{20}}\% $ एवं ${\mathbf{79}}\% $ के अनुपात में हैं। ${\mathbf{10}}$वायुमण्डल दाब पर जल वायु के साथ साम्य में है। ${\mathbf{298}}{\text{ }}{\mathbf{K}}$ पर यदि ऑक्सीजन तथा नाइट्रोजन के हेनरी स्थिरांक क्रमशः ${\mathbf{3}}.{\mathbf{30}}{\text{ }}{\mathbf{x}}{\text{ }}{\mathbf{107}}{\text{ }}{\mathbf{mm}}$ तथा ${\mathbf{6}}.{\mathbf{51}}{\text{ }}{\mathbf{x}}{\text{ }}{\mathbf{107}}{\text{ }}{\mathbf{mm}}$हैं तो जल में इन गैसों का संघटन ज्ञात कीजिए।$$

उत्तर:

वायु के जल के साथ साम्य पर कुल दाब $ = 10atm.$
∵ वायु में $20\% $ ऑक्सीजन तथा $79\% $ नाइट्रोजन आयतनानुसार उपस्थित हैं।
∴  ऑक्सीजन का आंशिक दाब 

${p_O}_{_2} = \dfrac{{20}}{{100}} \times 10atm$.

$ = 2atm.$

$ = 2 \times 760mm$

$ = 1520mm$

नाइट्रोजन का आंशिक दाब

${p_{{N_{_2}}}} = \dfrac{{79}}{{100}} \times 10atm$

$ = 7.9atm$

$ = 6004mm\;$

${K_H}\left( {{O_2}} \right) = 3.30 \times {10^7}mm$,

${K_H}\left( {{N_2}} \right) = 6.51 \times 107mm$ 

हेनरी के नियमानुसार, 

${p_{{O_2}}} = {K_H} \times {O_2}$

${x_{{O_2}}} = \dfrac{{P{O_2}}}{{{K_H}}}$

$ = \dfrac{{1520}}{{3.30 \times {{10}^7}}}$

$ = 4.61 \times {10^{ - 5}}$

${p_{{N_2}}} = {K_H} \times x{N_2}x{N_2}$

$ = \dfrac{{{p_{{N_2}}}}}{{{K_H}}}$

$ = \dfrac{{6004mm}}{{6.51 \times {{10}^7}mm}}$

$ = 9.22 \times {10^{ - 5}}\;$

40. यदि जल का परासरण दाब ${\mathbf{27}}^\circ {\mathbf{C}}$ पर ${\mathbf{0}}.{\mathbf{75}}$ वायुमण्डल हो तो ${\mathbf{2}}.{\mathbf{5}}$ लीटर जल में घुले ${\mathbf{CaC}}{{\mathbf{l}}_{\mathbf{2}}}{\text{ }}\left( {{\mathbf{i}}{\text{ }} = {\text{ }}{\mathbf{2}}.{\mathbf{47}}} \right)$ की मात्रा परिकलित कीजिए।

उत्तर:

$\pi  = iCRT = i\dfrac{n}{V}RT\;\;$ या 

$n\; = \dfrac{{\pi  \times V}}{{i \times R \times T}}\;\;$

$ = \dfrac{{0.75{\text{ }}atm \times 25{\text{ }}L}}{{2.47 \times 0.0821{\text{ }}L{\text{ }}atm{\text{ }}{K^{ - 1}}{\text{ }}mo{l^{ - 1}} \times 300{\text{ }}K\;\;}}$

$ = \dfrac{{1.875}}{{60.836}}$

$ = 0.0308{\text{ }}mol$

$CaC{l_2}$  का मोलर द्राव्य्मान       

$_\; = {\text{ }}{\mathbf{40}}{\text{ }} + {\text{ }}{\mathbf{2}}{\text{ }} \times {\text{ }}{\mathbf{35}}.{\mathbf{5}}$

$= {\text{ }}{\mathbf{111}}{\text{ }}{\mathbf{g}}{\text{ }}{\mathbf{mo}}{{\mathbf{l}}^{ - {\mathbf{1}}}}$

 धुली मत्रा           

$ = {\text{ }}{\mathbf{0}}.{\mathbf{03080}} \times {\mathbf{111g}}$

$ = {\text{ }}{\mathbf{3}}.{\mathbf{42}}{\text{ }}{\mathbf{g}}\;$

41. ${\mathbf{2}}$  लीटर जल में ${\mathbf{25}}^\circ {\mathbf{C}}$ पर ${{\mathbf{K}}_{\mathbf{2}}}{\mathbf{S}}{{\mathbf{O}}_{\mathbf{4}}}$ के ${\mathbf{25}}{\text{ }}{\mathbf{mg}}$ को घोलने पर बनने वाले विलयन का परासरण दाब, यह मानते हुए ज्ञात कीजिए कि ${{\mathbf{K}}_{\mathbf{2}}}{\mathbf{S}}{{\mathbf{O}}_{\mathbf{4}}}$ पूर्णतः वियोजित हो गया है।

उत्तर:

$n = \dfrac{{0.025}}{{174}}$

$ = 0.0001436V$

$ = 2\;litre$,

$T = 25C + 273$

$= 298K$

${K_2}S{O_4}$ वियोजित होकर दो ${K^ + }$ तथा एक $S{O_4}^{2 - }$ आयन देता है। अतः यह $3$ आयन देता है।$\therefore i = 3$

$\pi  = i\dfrac{n}{V}RT$

$= \dfrac{{3 \times 0.0001436 \times 0.0821 \times 298}}{2}$

$= 5.2 \times {10^{ - 3\;}}atm\;$

NCERT Solutions for Class 12 Chemistry Chapter 2 Solutions in Hindi

Chapter-wise NCERT Solutions are provided everywhere on the internet with an aim to help the students to gain a comprehensive understanding. Class 12 Chemistry Chapter 2 solution Hindi medium is created by our in-house experts keeping the understanding ability of all types of candidates in mind. NCERT textbooks and solutions are built to give a strong foundation to every concept. These NCERT Solutions for Class 12 Chemistry Chapter 2 in Hindi ensure a smooth understanding of all the concepts including the advanced concepts covered in the textbook.

NCERT Solutions for Class 12 Chemistry Chapter 2 in Hindi medium PDF download are easily available on our official website (vedantu.com). Upon visiting the website, you have to register on the website with your phone number and email address. Then you will be able to download all the study materials of your preference in a click. You can also download the Class 12 Chemistry Solutions solution Hindi medium from Vedantu app as well by following the similar procedures, but you have to download the app from Google play store before doing that. 

NCERT Solutions in Hindi medium have been created keeping those students in mind who are studying in a Hindi medium school. These NCERT Solutions for Class 12 Chemistry Solutions in Hindi medium pdf download have innumerable benefits as these are created in simple and easy-to-understand language. The best feature of these solutions is a free download option. Students of Class 12 can download these solutions at any time as per their convenience for self-study purpose. 

These solutions are nothing but a compilation of all the answers to the questions of the textbook exercises. The answers/solutions are given in a stepwise format and very well researched by the subject matter experts who have relevant experience in this field. Relevant diagrams, graphs, illustrations are provided along with the answers wherever required. In nutshell, NCERT Solutions for Class 12 Chemistry in Hindi come really handy in exam preparation and quick revision as well prior to the final examinations.