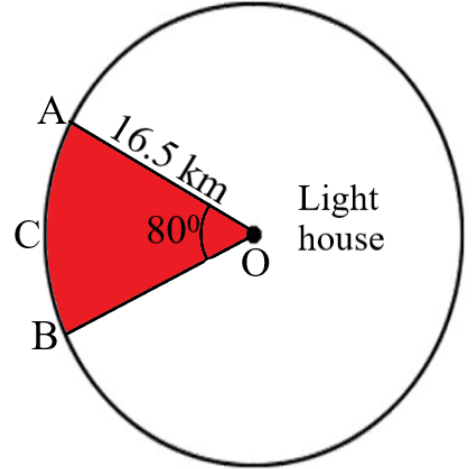
NCERT Solutions For Class 10 Maths Chapter 11 Areas Related To Circles Exercise 11.1 (2025-26): FREE PDF
Class 10 Maths Chapter 11 Exercise 11.1 Areas Related to Circles NCERT Solutions
FAQs on Class 10 Maths Chapter 11 Exercise 11.1 Areas Related to Circles NCERT Solutions
1. What are the key formulas covered in Class 10 Maths Chapter 11 Areas Related to Circles?
The main formulas include area of circle = πr², circumference = 2πr, area of sector = (θ/360°) × πr², and area of segment = area of sector - area of triangle. These formulas are essential for solving problems involving circular regions, sectors, and segments in geometry.
These formulas form the foundation for calculating areas and perimeters of circular shapes and their parts, which appear frequently in board exams and real-world applications like calculating land areas or material requirements.
2. How do NCERT Solutions for Areas Related to Circles help students understand Exercise 11.1?
NCERT Solutions provide detailed step-by-step explanations for each problem in Exercise 11.1, making complex circle area calculations easier to understand. Students benefit from clear reasoning behind each formula application and common problem-solving approaches.
Exercise 11.1 introduces fundamental concepts that build toward more complex problems in subsequent exercises, so mastering these basics is crucial for chapter success.
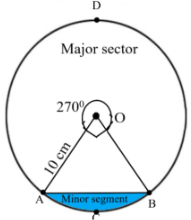
3. What is the difference between area of sector and area of segment in circles?
A sector is the region between two radii and an arc, while a segment is the region between a chord and the arc it subtends. The sector includes the triangular portion from the center, but the segment excludes it.
This distinction is crucial for solving problems correctly, as confusing these concepts leads to wrong formula application and incorrect answers in geometry problems.
4. Where can students access Class 10 Maths Chapter 11 Exercise 11.1 solutions for free?
Students can access comprehensive solutions through Vedantu's Free PDF downloads and online platform, which provide detailed explanations for all Exercise 11.1 problems. These resources include step-by-step solutions with diagrams and formula applications.
5. How to calculate the area of a circular ring or annulus?
The area of a circular ring equals the difference between the areas of outer and inner circles: Area = π(R² - r²), where R is the outer radius and r is the inner radius. This concept frequently appears in Class 10 areas related to circles problems.
Circular rings represent real-world scenarios like pathways around gardens, pipe cross-sections, or ring-shaped objects, making this calculation practically relevant.
6. What common mistakes do students make in Areas Related to Circles Exercise 11.1?
Students commonly confuse radius with diameter, use wrong units, forget to subtract areas in ring problems, and mix up sector and segment formulas. These errors significantly impact final answers and exam scores.
Understanding these pitfalls helps students avoid careless mistakes and improves accuracy in geometry problem-solving, especially during time-pressured exam situations.
7. How does understanding perimeter and area of circles help in real-life applications?
Circle area and perimeter calculations help solve practical problems like finding material needed for circular objects, calculating land areas, determining paint requirements, or designing circular structures. These concepts bridge classroom learning with everyday problem-solving.
Real-world applications make mathematical concepts more meaningful and help students see the practical value of their studies beyond exam preparation.
8. What study strategy works best for mastering Class 10 Maths Chapter 11 concepts?
Start with understanding basic formulas, practice solved examples, work through Exercise 11.1 systematically, and use visual aids like diagrams to grasp sector and segment concepts. Regular practice with varied problems builds strong conceptual understanding.
Areas related to circles requires both formula memorization and conceptual clarity, so a structured approach ensures comprehensive preparation for board exams.




















 Watch Video
Watch Video