




How to Find Factors of 7429: Methods and Examples
Factors of a number are integers that when divided by the given number leave remainder as 0. The integers that can divide 7429 evenly i.e., without any remainder are known as the factors of 7429. Finding the factors for bigger numbers like 7429, however, is challenging since it might be hard to determine the numbers that divide it exactly. We can use both the division and factor tree methods to identify the factors.
How to Find the Factors of 7429?
To understand how to find the factors of 7429, follow the steps provided below.
Step 1: Find the two integers that when multiplied together result in 7429, for example, $17\; \times \;437\; = \;7429$.
Step 2: We are aware that the number 17 is a prime number. Therefore, we are unable to factor it further.
Step 3: Let's now try with various multiplications of integers that result in the number 7429, such as
$19\; \times \;391\; = \;7429$
$23\; \times \;323\; = \;7429$
Therefore, 1, 17, 19, 23, 323, 391, 437, and 7429 are the factors of 7429.
Prime Factors of 7429
In order to find the prime factors of 7429, one can also use the factor tree method. A factor tree involves creating branches of prime numbers that are factors of the given number. The end numbers in the factor tree denote the prime factors of the given number.
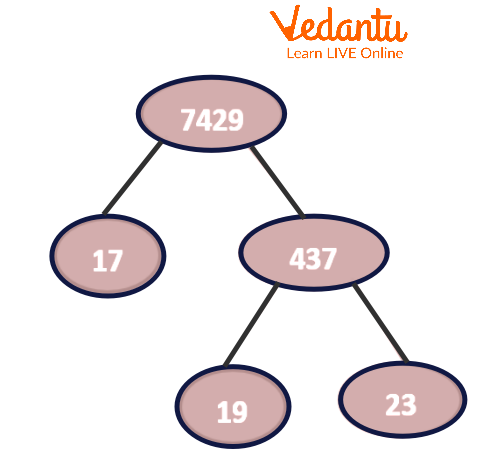
Factor Tree of 7429
Due to its composite nature, the number 7429 will have prime factors. The factor tree of 7429 as represented in the above image shows that 7429 has 3 prime factors namely 17, 19, and 23.
Prime Factorisation of 7429
Prime factorisation is the process of factorising a number into its prime numbers. This can be done by finding different prime numbers which divide the given number exactly, i.e., leaving the remainder as 0.
Let's figure out how to divide 7429 into its prime factors now.
Step 1: Divide the number 7429 by the lowest prime number, which is 2.
7429 ÷ 2 = 3714.5
Given that none of the factors may be a fraction, 2 is not the prime factor for the number 7429.
So go on to the following prime numbers, which are 3, 5, 7, and so on.
7429 ÷ 3 = 2476.33
7429 ÷ 5 = 1485.8
7429 ÷ 7 = 1061.2857
7429 ÷ 11 = 675.3636
7429 ÷ 13 = 571.4615
7429 ÷ 17 = 437.
Therefore 17 is a prime factor of 7429.
Step 2: We now divide 437 by 2.
437 ÷ 2 = 218.5
Since the factors must not be fractions, 2 is not the prime factor for 437.
Moving on to the prime numbers 3, 5, 7, and so on we get,
437÷ 3 = 145.66,
437÷ 5 = 87.5,
437÷ 7 = 62.4285,
437 ÷11 = 39.7272,
437÷ 13 = 33.6154,
437÷ 17 = 25.7058,
and 437÷ 19 = 23.
The division method cannot be used further since 19 and 23 are prime integers.
As a result, the prime factorisation of 7429 may be written as $17 \times 19 \times 23$ where 17, 19, and 23 are prime.
The following image represents the prime factorisation of 7429.

Prime Factorisation of 7429
Hence, $7429\; =17 \times 19 \times 23$
This can also be written in exponential notation as ${17^1} \times {19^1} \times {23^1}$.
Factor Pairs of 7429
The pairs of integers that, when multiplied, result in the number 7429 are known as the pair factors of 7429. The factors of 7429 in pairs are:
NOTE: If (a, b) is a pair factor, then (b, a) is also a pair factor.
Interesting Facts
A factor of a number is always less than or equal to the given number.
Every number except 0 and 1 has at least two factors, 1 and itself.
The LCM or HCF of two or more numbers can be determined using the prime factorisation of the corresponding number.
Solved Examples
1. What are the positive pair factors of 7429?
Solution: The positive pair factors of 7429 are (1, 7429), (17, 437), (19, 391), and (23,323).
2. Find the common factors of 7429 and 7433.
Solution: The factors of 7429 are 1, 17, 19, 23, 323, 391, 437, and 7429.The factors of 7433 are 1 and 7433. As 7433 is a prime number, the common factor of 7429 and 7433 is 1.
3. What is the sum of all the factors of the number 7429?
Solution: We know that factors of 7429 are:
1, 17, 19, 23, 323, 391, 437, and 7429.
Sum of all the factors = 1 +17 +19 +23 +323 +391 +437 +7429
Sum = 8640
Conclusion
The article summarises the process of finding the prime factors of 7429. Since 7429 is a composite number, it has 3 prime factors which are 17, 19, and 23. Except for the prime factors, there are other factors of 7429 namely 1, 323, 391, 437, and 7429 itself. The prime factorisation of $7429\;=\;17\; \times \;19\; \times \;23$. There are both positive and negative factor pairs of 7429.
Practice Questions
1. Using the factors of 7429, the HCF of 7429 and 1232 is:
1
11
23
19
Ans: a) 1
2. Two wires are 7429 cm and 5491 cm long. The wires are to be cut into pieces of equal length. The maximum length of each piece is:
5491
100
323
451
Ans: c) 323
3. The product of all prime factors of 7429 is:
439
23
323
7429
Ans: d) 7429
FAQs on What Are the Factors of 7429?
1. What are all the factors of 7429?
The factors of 7429 are all the whole numbers that divide it exactly without leaving a remainder. The complete list of factors for 7429 is 1, 17, 19, 23, 323, 391, 437, and 7429. Each of these numbers can be multiplied by another factor to equal 7429.
2. How do you find the prime factors of 7429 using the prime factorization method?
To find the prime factors of 7429, we start by dividing it by the smallest prime numbers. Since 7429 is not divisible by 2, 3, 5, 7, 11, or 13, we test the next prime, 17. The steps are:
1. Divide 7429 by 17: 7429 ÷ 17 = 437.
2. Now, find a prime factor for 437. We test primes and find it is divisible by 19: 437 ÷ 19 = 23.
3. The result, 23, is itself a prime number.
Thus, the prime factorization of 7429 is expressed as the product of its prime factors: 17 × 19 × 23.
3. Why is 7429 considered a composite number and not a prime number?
A prime number is a natural number greater than 1 that has only two factors: 1 and itself. A composite number has more than two factors. Since 7429 has factors other than 1 and 7429 (namely 17, 19, 23, 323, 391, and 437), it has more than two factors. Therefore, 7429 is classified as a composite number.
4. What is the difference between the 'factors' and 'prime factors' of 7429?
The term 'factors' refers to the complete set of numbers that divide 7429 without a remainder. In contrast, 'prime factors' are the specific factors from that list which are also prime numbers. For 7429:
- Factors: {1, 17, 19, 23, 323, 391, 437, 7429}
- Prime Factors: {17, 19, 23}
5. How can a factor tree be used to show the prime factorization of 7429?
A factor tree visually breaks down a number into its prime factors. For 7429, you would start with the number at the top. Draw two branches down to a pair of factors, for instance, 17 and 437. Since 17 is a prime number, that branch ends. You then break down 437 into its factors, 19 and 23. As both 19 and 23 are prime, these branches also end. The endpoints of the tree (17, 19, and 23) represent the prime factors.
6. What is the importance of expressing 7429 as a product of its primes (17 × 19 × 23) in mathematics?
Expressing 7429 as 17 × 19 × 23 is a direct application of the Fundamental Theorem of Arithmetic from the Class 10 syllabus. This theorem states that every composite number can be written as a unique product of prime numbers. This unique prime factorization is essential for advanced concepts like finding the Highest Common Factor (HCF) and Lowest Common Multiple (LCM) of numbers, which is a key skill in solving various mathematical problems.
7. How can the prime factors of 7429 help find its HCF with another number, like 391?
To find the Highest Common Factor (HCF) of 7429 and 391, we use their prime factorizations:
- Prime factorization of 7429 = 17 × 19 × 23
- Prime factorization of 391 = 17 × 23




























