




How to Find All Factors and Prime Factors of 180
In this article, we will explore the factors of 180, pair factors, and the prime factorisation of 180, as well as solve examples for better understanding.
To get the pair factor of 180, multiply the two numbers in a pair to obtain the original number, which is 180. A factor of 180 will divide it equally. Those factors cannot be of a fractional or decimal value. 180 has a total of 12 factors. The factors are 1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 30, 36, 45, 60, 90 and 180. The sum of all factors of 180 is 546.
What are the Factors of 180?
Factors of 180 are the numbers that divide 180 exactly with no remainder. Since the number 180 is even composite, it has many factors other than 1 and 180. As a result, the factors of 180 are 1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 30, 36, 45, 60, 90 and 180.
How to Find the Factors of 180?
The factors of 180 are the numbers that divide 180 exactly without the remainder. Therefore, the method for identifying and listing all of the factors of 180 is to count every integer from 1 to 180 and determine which values have an even quotient (which means no decimal place).
Here are all the factors for 180:
\[180\text{ }\div \text{ }1\text{ }=\text{ }180\]
1 is a factor of 180.
\[180\div 2=90\]
2 is a factor of 180.
\[180\text{ }\div \text{ }3\text{ }=\text{ }60\]
3 is a factor of 180.
\[180\text{ }\div \text{ }4\text{ }=\text{ }45\]
4 is a factor of 180.
\[180\text{ }\div \text{ }5\text{ }=\text{ }36\]
5 is a factor of 180.
\[180\text{ }\div \text{ }6\text{ }=\text{ }30\]
6 is a factor of 180.
\[180\text{ }\div \text{ }9\text{ }=\text{ }20\]
9 is a factor of 180.
\[180\text{ }\div \text{ }10\text{ }=\text{ }18\]
10 is a factor of 180.
\[180\text{ }\div \text{ }12\text{ }=\text{ }15\]
12 is a factor of 180.
\[180\text{ }\div \text{ }15\text{ }=\text{ }12\]
15 is a factor of 180.
\[180\text{ }\div \text{ }18\text{ }=\text{ }10\]
18 is a factor of 180.
\[180\text{ }\div \text{ }20\text{ }=\text{ }9\]
20 is a factor of 180.
\[180\text{ }\div \text{ }30\text{ }=\text{ }6\]
30 is a factor of 180.
\[180\text{ }\div \text{ }36\text{ }=\text{ }5\]
36 is a factor of 180.
\[180\text{ }\div \text{ }45\text{ }=\text{ }4\]
45 is a factor of 180.
\[180\text{ }\div \text{ }60\text{ }=\text{ }3\]
60 is a factor of 180.
\[180\text{ }\div \text{ }90\text{ }=\text{ }2\]
90 is a factor of 180.
\[180\text{ }\div \text{ }180\text{ }=\text{ }1\]
180 is a factor of 180.
Thus, all the factors of 180 are 1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 30, 36, 45, 60, 90 and 180.
What is the Prime Factorization of 180?
180 is a composite number that should have prime factors. Prime factorisation of 180 refers to determining the prime factors of 180. Divide 180 by the smallest prime number possible to get the prime factor of 180. Then, take the result and divide it by the lowest prime number. Continue this process until you get 1.
Step 1: Divide 180 by the lowest prime number, i.e., 2
\[180\text{ }\div \text{ }2\text{ }=\text{ }90\]
Step 2: Again divide 90 by 2;
\[90\text{ }\div \text{ }2\text{ }=\text{ }45\]
So 2 can’t be a factor of 45, so go to the next prime number, i.e., 3.
Step 3: Divide 45 by 3;
\[45\div 3=15\]
Step 4: Divide 15 by 3;
\[15\text{ }\div \text{ }3\text{ }=\text{ }5\]
Step 5: Divide 5 by 5;
\[5\text{ }\div \text{ }5\text{ }=\text{ }1\]
Thus, we get 1 at the end of this division method, and we can’t go on with the division approach. Hence, the prime factorisation of 180 is \[2\text{ }\times \text{ }2\text{ }\times \text{ }3\text{ }\times \text{ }3\text{ }\times \text{ }5\] or \[{{2}^{2}}\times \text{ }{{3}^{2}}\times \text{ }5\] where 2, 3, and 5 are prime numbers.
Factor Tree of 180
Factor trees represent the factors of a number, especially its prime factorisation. Each tree branch is divided into factors. The end of the branch in the factor tree must be a prime number because the only two factors are itself and one, so the branch stops.
We should also remember that 1 is not a prime number; thus, it will not appear in any factor tree.
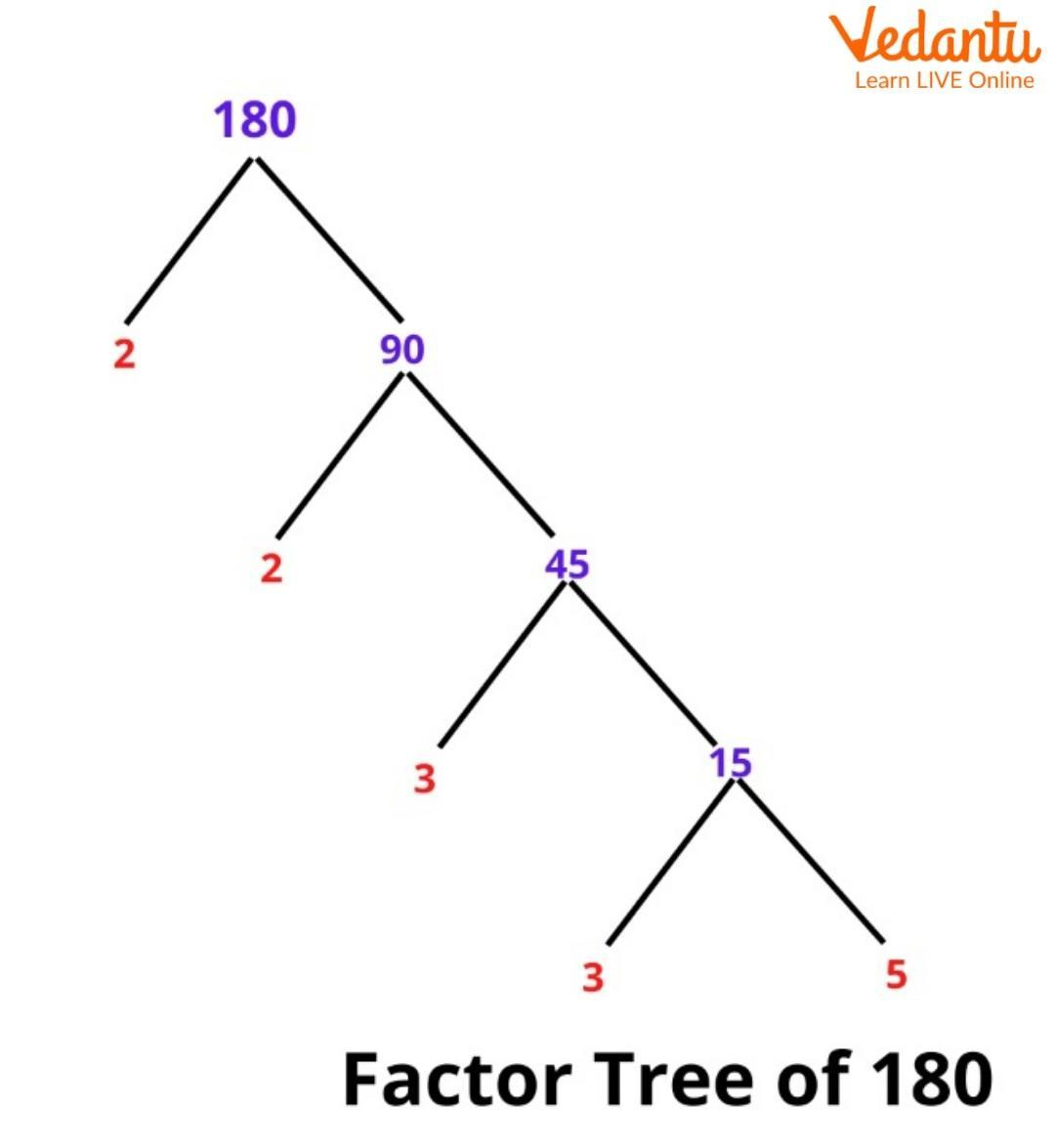
Factor Tree of 180
Negative Factors of a Number
A number's factors include all of the numbers that can be multiplied by one another to get that number. A negative number always contains one negative element. As a result, when we multiply two negative numbers then eventually we end up getting a positive number as a product. Here the negative factors of 180 are -1, -2, -3, -4, -5, -6, -9, -10, -12, -15, -18, -20, -30, -36, -45, -60, -90 and \[-180\].
Sum of Factors of 180
To get the sum of factors of a number, we have to add all the factors of that number. Here, all factors of 180 are 1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 30, 36, 45, 60, 90 and 180. So, the sum of factors of 180 is 1 + 2 + 3 + 4 + 5 + 6 + 9 + 10 + 12 + 15 + 18 + 20 + 30 + 36 + 45 + 60 + 90 + 180 = 546.
Pair Factors of 180
When multiplied in pairs, the numbers that provide the original number, i.e. 180 are known as 180's pair factors. The pair factors of 180 might have both positive and negative values.
Thus, the positive pair factors are \[\left( 1,\text{ }180 \right),\text{ }\left( 2,\text{ }90 \right),\text{ }\left( 3,\text{ }60 \right),\text{ }\left( 4,\text{ }45 \right),\text{ }\left( 5,\text{ }36 \right),\text{ }\left( 6,\text{ }30 \right),\text{ }\left( 9,\text{ }20 \right),\text{ }\left( 10,\text{ }18 \right)\] and \[\left( 12,\text{ }15 \right)\].
Thus, the negative pair factors are \[\left( -1,\text{ }-180 \right),\text{ }\left( -2,\text{ }-90 \right),\text{ }\left( -3,\text{ }-60 \right),\text{ }\left( -4,\text{ }-45 \right),\text{ }\left( -5,\text{ }-36 \right),\text{ }\left( -6,\text{ }-30 \right),\text{ }\left( -9,\text{ }-20 \right),\text{ }\left( -10,\text{ }-18 \right)\] and \[\left( -12,\text{ }-15 \right)\].
Interesting Facts
The pair factors of 180 might have both positive and negative values. For example, The pair factors of 180 might be \[(1,180)\] or \[(-1,-180)\]. When two negative numbers are multiplied, such as when \[-1\] and \[-180\] are multiplied, the answer is 180.
1 is the factor for each number, as 1 times a number is the number itself. Again, anything divided by 1 is the number itself.
Solved Examples
1. Write common factors of 150 and 180.
Ans: An integer that divides the original number into equal parts without a remainder is called a factor. Thus, we know that the factors of 150 and 180 are 1, 2, 3, 5, 6, 10, 15, 25, 30, 50, 75, 150 and 1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 30, 36, 45, 60, 90, 180, respectively.
Thus, the common factors of 150 and 180 are 1, 2, 3, 5, 6, 10, 15 and 30.
2. Write all the factors of 13 and the prime factorization of 13.
Ans: The numbers that exactly divides 13 without leaving a remainder are known as the factors of 13. We know that the number 13 is divisible by 1 and 13. As a result, all of these integers are called the factors of 13.
13 is a prime number, which means it has only 2 factors. We know that the factors of 13 are 1 and 13. Thus, the prime factorization of 13 is \[1\times 13\].
3. Write negative pair factors of 180.
Ans: The pair factors of 180 might have both positive and negative values. For example, The pair factors of 180, might be \[(1,180)\] or \[(-1,-180)\]. Thus, the negative pair factors of 180 are (-1, -180), (-2, -90), (-3, -60), (-4, -45), (-5, -36), (-6, -30), (-9, -20), (-10, -18) and (-12, -15).
Practice Questions
1. How many positive pair factors does 180 have?
7
8
9
10
2. What is the sum of the factors of 180?
540
546
246
446
Answers:
C
B
Conclusion
Hence, the number 180 is even composite, it has many factors other than 1 and 180. The factors of 180 are the numbers that divide 180 exactly without the remainder. Thus, the factors are 1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 30, 36, 45, 60, 90 and 180. Thus, the prime factor of 180 is \[2\times 2\times 3\times 3\times 5\] or \[{{2}^{2}}\times {{3}^{2}}\times 5\] where 2, 3, and 5 are prime numbers.
FAQs on Factors of 180: Step-by-Step Prime Factorization
1. What are all the factors of 180?
The factors of 180 are all the whole numbers that divide 180 without leaving a remainder. The factors are 1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 30, 36, 45, 60, 90, and 180.
2. How do you find the prime factorization of 180 using the division method?
To find the prime factorization of 180 by the division method, you repeatedly divide the number by the smallest prime numbers until the quotient is 1. The steps are as follows:
- Start with 180 and divide by the smallest prime factor, 2: 180 ÷ 2 = 90.
- Divide 90 by 2 again: 90 ÷ 2 = 45.
- Since 45 is not divisible by 2, use the next prime factor, 3: 45 ÷ 3 = 15.
- Divide 15 by 3 again: 15 ÷ 3 = 5.
- Finally, divide 5 by the next prime factor, 5: 5 ÷ 5 = 1.
The prime factors are the divisors used: 2, 2, 3, 3, and 5.
3. How can the factor tree method be used to find the prime factors of 180?
The factor tree method breaks down a number into its factors until only prime numbers remain. For 180, the process is:
- Start with 180 at the top.
- Branch it into a pair of factors, for example, 10 and 18.
- Break down 10 into its prime factors: 2 and 5. Circle these as they are prime.
- Break down 18 into its factors, like 2 and 9. Circle the 2.
- Finally, break down 9 into its prime factors: 3 and 3. Circle both 3s.
The prime factors of 180 are the numbers at the end of the branches: 2 × 2 × 3 × 3 × 5.
4. How is the prime factorization of 180 expressed in exponential form?
First, find the prime factors of 180, which are 2, 2, 3, 3, and 5. To express this in exponential form, group the identical prime factors and write them as a power. There are two 2s (2²), two 3s (3²), and one 5 (5¹). Therefore, the prime factorization of 180 in exponential form is 2² × 3² × 5¹.
5. What is the difference between 'factors' and 'prime factors' of 180?
The terms 'factors' and 'prime factors' are related but distinct concepts:
- Factors of 180 are all the integers that divide 180 evenly. This includes both prime and composite numbers, such as 1, 4, 6, 9, 10, 12, etc.
- Prime factors of 180 are the specific factors of 180 that are also prime numbers. For 180, the only prime factors are 2, 3, and 5. These are the fundamental building blocks of the number.
6. Why is prime factorization a more powerful tool than just listing all factors?
Prime factorization is more powerful because it provides a unique 'fingerprint' for any composite number. Unlike a simple list of factors, the prime factorization (e.g., 2² × 3² × 5¹ for 180) is unique and helps to:
- Easily calculate the Highest Common Factor (HCF) and Lowest Common Multiple (LCM) with other numbers.
- Determine if a number is a perfect square or a perfect cube by checking if the exponents of its prime factors are all even or multiples of three, respectively.
- Simplify complex fractions and algebraic expressions.
7. How does knowing the prime factors of 180 help find its HCF with another number, like 72?
Using prime factors makes finding the Highest Common Factor (HCF) straightforward. First, find the prime factorization of both numbers:
- Prime factorization of 180 = 2² × 3² × 5¹
- Prime factorization of 72 = 2³ × 3²
To find the HCF, you take the lowest power of each common prime factor. The common prime factors are 2 and 3. The lowest power of 2 is 2² and the lowest power of 3 is 3². Therefore, the HCF is 2² × 3² = 4 × 9 = 36.
8. Is 180 a perfect square? How can its prime factorization prove this?
No, 180 is not a perfect square. The prime factorization of a number can instantly tell you if it's a perfect square. A number is a perfect square only if all the exponents in its prime factorization are even numbers.
The prime factorization of 180 is 2² × 3² × 5¹. While the exponents for 2 and 3 are even (2), the exponent for 5 is 1, which is an odd number. Because of this, 180 cannot be a perfect square.








































