Answer
Verified98.1k+ views
Hint: First draw a picture of the given scenario then send multiple rays from the object to the mirror and they are reflected by the mirror planes. Now, draw a circle whose centre is the intersection point of two mirror planes. After that, find the number of points on the circle which intersect with the extended line of one reflected ray and one incident and that is the number of images formed.
Complete step by step solution:
The light is thrown back by a body or surface without absorbing it is called reflection of light. Plane mirror is a smooth surface. For the smooth surfaces, the incident angle of light is exactly the same as the reflected angle. The incident angle and the reflected angles are measured with respect to the normal to the mirror.
Let’s try to solve the questions together. See here is a mirror with two planes inclined at ${72^0}$ with each other. First let’s take a picture and try to find the number of images formed by two planes inclined at an angle ${72^0}$.
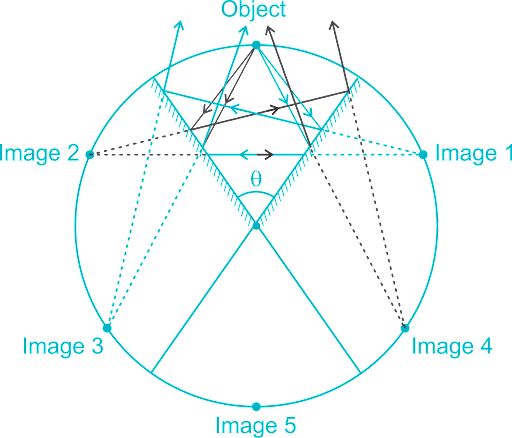
Here we observe the image and we can easily say that there are $4$ images in total. Now explain how we can draw that picture. Actually, we send multiple rays from the object to the mirror and they are reflected by the mirror planes.
Now we draw a circle whose centre is the intersection point of two mirror planes. then we find the number of points on the circle which are intersecting with the extended line of one reflected ray and one incident. We show our incident with sky blue colour and reflected rays are shown by darker shades of blue. Like that we get 4 points. So, there is a point between them. Let's now do a trick for this kind of question. so, 4 is our final answer.
Hence option C is the correct answer.
Note: The trick is to find out the number of images of mirrors inclined at an angle. Let's talk about that. Consider two mirror planes inclined to each other at an angle $\theta $ with each other and $n$is the number of images formed. Then, if $\dfrac{{{{360}^0}}}{\theta }$ is an integer then \[\dfrac{{{{360}^0}}}{\theta } - 1\] is the number of images. But if the $\dfrac{{{{360}^0}}}{\theta }$ is odd and object is not placed not in the angular bisector of the inclined mirror planes then number of images will $\dfrac{{{{360}^0}}}{\theta }$ . Here we consider that image is placed at the angular bisector of the planes. Another case where $\dfrac{{{{360}^0}}}{\theta }$ is not an integer. For that you have to check the number of images by the above mentioned method.
Complete step by step solution:
The light is thrown back by a body or surface without absorbing it is called reflection of light. Plane mirror is a smooth surface. For the smooth surfaces, the incident angle of light is exactly the same as the reflected angle. The incident angle and the reflected angles are measured with respect to the normal to the mirror.
Let’s try to solve the questions together. See here is a mirror with two planes inclined at ${72^0}$ with each other. First let’s take a picture and try to find the number of images formed by two planes inclined at an angle ${72^0}$.
Here we observe the image and we can easily say that there are $4$ images in total. Now explain how we can draw that picture. Actually, we send multiple rays from the object to the mirror and they are reflected by the mirror planes.
Now we draw a circle whose centre is the intersection point of two mirror planes. then we find the number of points on the circle which are intersecting with the extended line of one reflected ray and one incident. We show our incident with sky blue colour and reflected rays are shown by darker shades of blue. Like that we get 4 points. So, there is a point between them. Let's now do a trick for this kind of question. so, 4 is our final answer.
Hence option C is the correct answer.
Note: The trick is to find out the number of images of mirrors inclined at an angle. Let's talk about that. Consider two mirror planes inclined to each other at an angle $\theta $ with each other and $n$is the number of images formed. Then, if $\dfrac{{{{360}^0}}}{\theta }$ is an integer then \[\dfrac{{{{360}^0}}}{\theta } - 1\] is the number of images. But if the $\dfrac{{{{360}^0}}}{\theta }$ is odd and object is not placed not in the angular bisector of the inclined mirror planes then number of images will $\dfrac{{{{360}^0}}}{\theta }$ . Here we consider that image is placed at the angular bisector of the planes. Another case where $\dfrac{{{{360}^0}}}{\theta }$ is not an integer. For that you have to check the number of images by the above mentioned method.
Recently Updated Pages
Write a composition in approximately 450 500 words class 10 english JEE_Main
Arrange the sentences P Q R between S1 and S5 such class 10 english JEE_Main
Write an article on the need and importance of sports class 10 english JEE_Main
Name the scale on which the destructive energy of an class 11 physics JEE_Main
Choose the exact meaning of the given idiomphrase The class 9 english JEE_Main
Choose the one which best expresses the meaning of class 9 english JEE_Main