
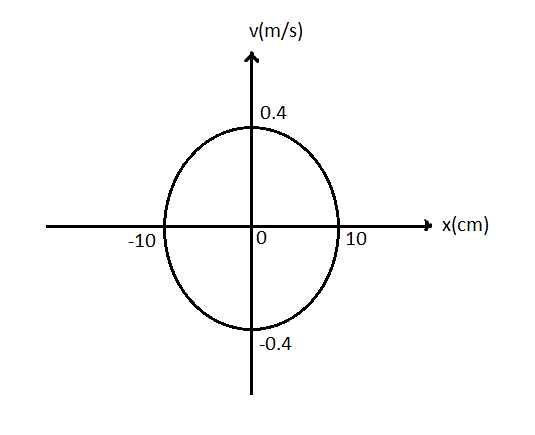
The plot velocity (v) versus displacement (x) of a particle executing simple harmonic motion in the figure. The time period of oscillation of particle is:
A) $\dfrac{\pi }{2}s$
B) $\pi s$
C) $2\pi s$
D) $3\pi s$
Answer
144.6k+ views
Hint:
A simple harmonic motion is an example of periodic motion. In simple harmonic motion, a particle is accelerated towards a fixed point (in this case, O) and the acceleration of the particle will be proportional to the magnitude of the displacement of the particle. We have to use the velocity and amplitude of the particle, which is given in the diagram to find the angular velocity. The time period can be calculated from that.
Formula used:
${v_{\max }} = A\omega $ (Where ${v_{\max }}$stands for the maximum velocity of the particle, $A$is the amplitude of the particle, $\omega $is the angular velocity of the particle)
$T = \dfrac{{2\pi }}{\omega }$ (Where $T$is the time period of oscillation, $2\pi $is a constant)
Complete step by step solution:
In the velocity-displacement graph given in the question, the $x$axis gives the value of displacement and the \[y\]axis gives the value of velocity.
For a simple harmonic oscillator, the maximum velocity is given by
${v_{\max }} = A\omega $
From this equation, the angular velocity can be deduced as
$\omega = \dfrac{{{v_{\max }}}}{A}$………………………..($1$)
From the graph,
The maximum displacement of the particle i.e. the amplitude,$A = 10cm$$ = 10 \times {10^{ - 2}}m$ $(\because 1cm = {10^{ - 2}}m)$
The maximum velocity of the particle, ${v_{\max }} = 0.4m/s$
Substituting the values $A$ and $\omega $ in equation ($1$)
$\omega = \dfrac{{0.4}}{{10 \times {{10}^{ - 2}}}} = 4{s^{ - 1}}$
The time period of a simple harmonic oscillator is given by,
$T = \dfrac{{2\pi }}{\omega }$
Substituting the value of $\omega $in the equation,
$T$ = $\dfrac{{2\pi }}{4} = \dfrac{\pi }{2}s$
The answer is Option (A), $\dfrac{\pi }{2}s.$
Note: The typical example of simple harmonic motion is the oscillation of a mass suspended at the end of a spring. The fixed point from which the particle starts moving is called the equilibrium position. The restoring force directed towards the equilibrium position will obey Hooke’s law. All simple harmonic motions are periodic but all periodic motions are not simple harmonic.
A simple harmonic motion is an example of periodic motion. In simple harmonic motion, a particle is accelerated towards a fixed point (in this case, O) and the acceleration of the particle will be proportional to the magnitude of the displacement of the particle. We have to use the velocity and amplitude of the particle, which is given in the diagram to find the angular velocity. The time period can be calculated from that.
Formula used:
${v_{\max }} = A\omega $ (Where ${v_{\max }}$stands for the maximum velocity of the particle, $A$is the amplitude of the particle, $\omega $is the angular velocity of the particle)
$T = \dfrac{{2\pi }}{\omega }$ (Where $T$is the time period of oscillation, $2\pi $is a constant)
Complete step by step solution:
In the velocity-displacement graph given in the question, the $x$axis gives the value of displacement and the \[y\]axis gives the value of velocity.
For a simple harmonic oscillator, the maximum velocity is given by
${v_{\max }} = A\omega $
From this equation, the angular velocity can be deduced as
$\omega = \dfrac{{{v_{\max }}}}{A}$………………………..($1$)
From the graph,
The maximum displacement of the particle i.e. the amplitude,$A = 10cm$$ = 10 \times {10^{ - 2}}m$ $(\because 1cm = {10^{ - 2}}m)$
The maximum velocity of the particle, ${v_{\max }} = 0.4m/s$
Substituting the values $A$ and $\omega $ in equation ($1$)
$\omega = \dfrac{{0.4}}{{10 \times {{10}^{ - 2}}}} = 4{s^{ - 1}}$
The time period of a simple harmonic oscillator is given by,
$T = \dfrac{{2\pi }}{\omega }$
Substituting the value of $\omega $in the equation,
$T$ = $\dfrac{{2\pi }}{4} = \dfrac{\pi }{2}s$
The answer is Option (A), $\dfrac{\pi }{2}s.$
Note: The typical example of simple harmonic motion is the oscillation of a mass suspended at the end of a spring. The fixed point from which the particle starts moving is called the equilibrium position. The restoring force directed towards the equilibrium position will obey Hooke’s law. All simple harmonic motions are periodic but all periodic motions are not simple harmonic.
Recently Updated Pages
Difference Between Vapor and Gas: JEE Main 2024

Area of an Octagon Formula - Explanation, and FAQs

Charle's Law Formula - Definition, Derivation and Solved Examples

Central Angle of a Circle Formula - Definition, Theorem and FAQs

Average Force Formula - Magnitude, Solved Examples and FAQs

Boyles Law Formula - Boyles Law Equation | Examples & Definitions

Trending doubts
JEE Main 2025 Session 2: Application Form (Out), Exam Dates (Released), Eligibility, & More

JEE Main 2025: Derivation of Equation of Trajectory in Physics

JEE Main Exam Marking Scheme: Detailed Breakdown of Marks and Negative Marking

Electric Field Due to Uniformly Charged Ring for JEE Main 2025 - Formula and Derivation

Learn About Angle Of Deviation In Prism: JEE Main Physics 2025

Degree of Dissociation and Its Formula With Solved Example for JEE

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Units and Measurements Class 11 Notes: CBSE Physics Chapter 1

NCERT Solutions for Class 11 Physics Chapter 1 Units and Measurements

Motion in a Straight Line Class 11 Notes: CBSE Physics Chapter 2

JEE Advanced 2025: Dates, Registration, Syllabus, Eligibility Criteria and More

JEE Advanced Weightage 2025 Chapter-Wise for Physics, Maths and Chemistry




