
The average P.E. of a body executing S.H.M. is :
\[
\left( 1 \right)\dfrac{1}{2}k{A^2} \\
\left( 2 \right)\dfrac{1}{4}k{A^2} \\
\left( 3 \right)3k{A^2} \\
\left( 4 \right)zero \\
\]
Answer
146.7k+ views
Hint:Law of conservation of energy states that the total of all forms of energies possessed by a moving object is always constant.
During any process energy can neither be created nor be destroyed it can be only converted from one form to another
In SHM the potential energy of the system is continuously converting from potential energy to kinetic energy and the again to potential energy
Complete step by step solution:
Simple harmonic motion:
repetitive movement back and forth through an equilibrium, or central, position, so that the maximum displacement on one side of this position is equal to the maximum displacement on the other side.
In SHM the potential energy of any object is maximum at the two far ends and the kinetic energy is maximum at the midpoint
Refer figure:
Now as we know that the motion of the block on a spring in SHM is defined by the position \[x\left( t \right) = A\cos \left( {\omega t + \phi } \right)\]_______________$\left( 1 \right)$
We know that derivating position to time we get velocity,
So \[v(t) = - A\omega {\text{sin}}(\omega t + \phi )\]___________________________$\left( 2 \right)$
As per the law of conservation of energy
Total energy = Kinetic energy $ + $Potential energy
$ \Rightarrow {E_{total}} = \dfrac{1}{2}m{v^2} + \dfrac{1}{2}k{x^2}$
Where
$m$: the mass of the block
k: spring constant
v: velocity of the object
x: displacement
\[{E_{total}} = \dfrac{1}{2}m{A^2}{\omega ^2}{\sin ^2}\left( {\omega t + \phi } \right) + \dfrac{1}{2}k{A^2}{\cos ^2}\left( {\omega t + \phi } \right)\]
As \[\omega = \sqrt {\dfrac{k}{m}} \]
\[
\therefore {E_{total}} = \dfrac{1}{2}m{A^2}\left( {\dfrac{k}{m}} \right){\sin ^2}\left( {\omega t + \phi } \right) + \dfrac{1}{2}k{A^2}{\cos ^2}\left( {\omega t + \phi } \right) \\
\Rightarrow {E_{total}} = \dfrac{1}{2}k{A^2}{\sin ^2}\left( {\omega t + \phi } \right) + \dfrac{1}{2}k{A^2}{\cos ^2}\left( {\omega t + \phi } \right) \\
\Rightarrow {E_{total}} = \dfrac{1}{2}k{A^2}\left[ {{{\sin }^2}\left( {\omega t + \phi } \right) + {{\cos }^2}\left( {\omega t + \phi } \right)} \right] \\
\\
\]
Again as ${\sin ^2}\theta + {\cos ^2}\theta = 1$
We get \[{E_{total}} = \dfrac{1}{2}k{A^2}\]______________________________(3)
Now to find average potential energy we know that in SHM as K.E increases P.E decreases and vice versa but total energy at all the points remains the same as the sum of K.E and P.E. from here we can conclude that average potential energy will be half of the total energy.
Refer figure:
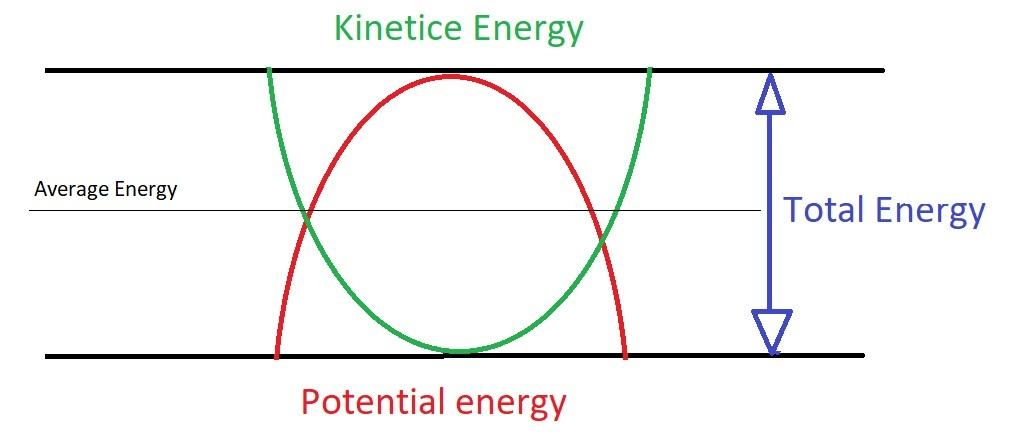
So,
\[
{\left( {P.E} \right)_{avg}} = \dfrac{{{E_{total}}}}{2} \\
\therefore {\left( {P.E} \right)_{avg}} = \dfrac{{\dfrac{1}{2}k{A^2}}}{2} \\
\Rightarrow {\left( {P.E} \right)_{avg}} = \dfrac{{k{A^2}}}{4} \\
\]
(2) The average potential energy of an object in SHM will be \[{\left( {P.E} \right)_{avg}} = \dfrac{{k{A^2}}}{4}\]
Note:
1) Energy is always conserved i.e.; the sum of all energies remains constant
2) As the object moves from an extreme position to the centre it's kinetic energy will increase from zero to maximum and then as it again moves from centre to another end it will decrease from a maximum at the centre to zero at ends.
3) The potential energy of the object is maximum at the end to zero at the centre
4) At every point in SHM, the total of kinetic energy and potential energy remains constant throughout.
During any process energy can neither be created nor be destroyed it can be only converted from one form to another
In SHM the potential energy of the system is continuously converting from potential energy to kinetic energy and the again to potential energy
Complete step by step solution:
Simple harmonic motion:
repetitive movement back and forth through an equilibrium, or central, position, so that the maximum displacement on one side of this position is equal to the maximum displacement on the other side.
In SHM the potential energy of any object is maximum at the two far ends and the kinetic energy is maximum at the midpoint
Refer figure:

Now as we know that the motion of the block on a spring in SHM is defined by the position \[x\left( t \right) = A\cos \left( {\omega t + \phi } \right)\]_______________$\left( 1 \right)$
We know that derivating position to time we get velocity,
So \[v(t) = - A\omega {\text{sin}}(\omega t + \phi )\]___________________________$\left( 2 \right)$
As per the law of conservation of energy
Total energy = Kinetic energy $ + $Potential energy
$ \Rightarrow {E_{total}} = \dfrac{1}{2}m{v^2} + \dfrac{1}{2}k{x^2}$
Where
$m$: the mass of the block
k: spring constant
v: velocity of the object
x: displacement
\[{E_{total}} = \dfrac{1}{2}m{A^2}{\omega ^2}{\sin ^2}\left( {\omega t + \phi } \right) + \dfrac{1}{2}k{A^2}{\cos ^2}\left( {\omega t + \phi } \right)\]
As \[\omega = \sqrt {\dfrac{k}{m}} \]
\[
\therefore {E_{total}} = \dfrac{1}{2}m{A^2}\left( {\dfrac{k}{m}} \right){\sin ^2}\left( {\omega t + \phi } \right) + \dfrac{1}{2}k{A^2}{\cos ^2}\left( {\omega t + \phi } \right) \\
\Rightarrow {E_{total}} = \dfrac{1}{2}k{A^2}{\sin ^2}\left( {\omega t + \phi } \right) + \dfrac{1}{2}k{A^2}{\cos ^2}\left( {\omega t + \phi } \right) \\
\Rightarrow {E_{total}} = \dfrac{1}{2}k{A^2}\left[ {{{\sin }^2}\left( {\omega t + \phi } \right) + {{\cos }^2}\left( {\omega t + \phi } \right)} \right] \\
\\
\]
Again as ${\sin ^2}\theta + {\cos ^2}\theta = 1$
We get \[{E_{total}} = \dfrac{1}{2}k{A^2}\]______________________________(3)
Now to find average potential energy we know that in SHM as K.E increases P.E decreases and vice versa but total energy at all the points remains the same as the sum of K.E and P.E. from here we can conclude that average potential energy will be half of the total energy.
Refer figure:

So,
\[
{\left( {P.E} \right)_{avg}} = \dfrac{{{E_{total}}}}{2} \\
\therefore {\left( {P.E} \right)_{avg}} = \dfrac{{\dfrac{1}{2}k{A^2}}}{2} \\
\Rightarrow {\left( {P.E} \right)_{avg}} = \dfrac{{k{A^2}}}{4} \\
\]
(2) The average potential energy of an object in SHM will be \[{\left( {P.E} \right)_{avg}} = \dfrac{{k{A^2}}}{4}\]
Note:
1) Energy is always conserved i.e.; the sum of all energies remains constant
2) As the object moves from an extreme position to the centre it's kinetic energy will increase from zero to maximum and then as it again moves from centre to another end it will decrease from a maximum at the centre to zero at ends.
3) The potential energy of the object is maximum at the end to zero at the centre
4) At every point in SHM, the total of kinetic energy and potential energy remains constant throughout.
Recently Updated Pages
How to find Oxidation Number - Important Concepts for JEE

How Electromagnetic Waves are Formed - Important Concepts for JEE

Electrical Resistance - Important Concepts and Tips for JEE

Average Atomic Mass - Important Concepts and Tips for JEE

Chemical Equation - Important Concepts and Tips for JEE

Concept of CP and CV of Gas - Important Concepts and Tips for JEE

Trending doubts
JEE Main 2025 Session 2: Application Form (Out), Exam Dates (Released), Eligibility, & More

JEE Main Exam Marking Scheme: Detailed Breakdown of Marks and Negative Marking

JEE Main 2025: Derivation of Equation of Trajectory in Physics

Electric Field Due to Uniformly Charged Ring for JEE Main 2025 - Formula and Derivation

JEE Main Participating Colleges 2024 - A Complete List of Top Colleges

Degree of Dissociation and Its Formula With Solved Example for JEE

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

JEE Advanced 2025: Dates, Registration, Syllabus, Eligibility Criteria and More

Units and Measurements Class 11 Notes: CBSE Physics Chapter 1

NCERT Solutions for Class 11 Physics Chapter 1 Units and Measurements

Motion in a Straight Line Class 11 Notes: CBSE Physics Chapter 2

JEE Advanced Weightage 2025 Chapter-Wise for Physics, Maths and Chemistry




