




How to Calculate Equivalent Capacitance in Series and Parallel Combinations
The Combination Of Capacitors is a crucial topic in JEE Main Physics, helping students understand how to configure capacitors to achieve the desired electrical properties in circuits. By connecting capacitors in series or parallel, circuits can store, manage, and distribute charge effectively—vital in practical electronics, power supplies, and signal regulation.
Suppose you need either more or less capacitance in a circuit than a single capacitor provides. By arranging multiple capacitors either end-to-end (series) or side-by-side (parallel), you can fine-tune both the total charge storage and withstand the required voltages. Understanding the logic, formulas, and pitfalls in solving such problems is essential for top performance in JEE Physics exams.
What is a Combination Of Capacitors?
A combination of capacitors means joining two or more capacitors together in a specific manner—either in series or parallel—to adjust net capacitance for circuit requirements. This is widely used to optimize circuit performance, distribute voltage, or handle more charge than a single unit allows.
Types of Capacitor Combinations: Series vs. Parallel
The two primary modes of combining capacitors are series and parallel arrangements. Each changes the overall (equivalent) capacitance differently, and is chosen based on the need for voltage rating or charge storage.
| Arrangement | Visual Representation | Equivalent Capacitance Formula | Key Features |
|---|---|---|---|
| Series | [C1]—[C2]—[C3] | 1/Ceq = 1/C1 + 1/C2 + ... | Same charge, voltage divides, Ceq decreases |
| Parallel | [C1] [C2] [C3] |
Ceq = C1 + C2 + ... | Same voltage, charge divides, Ceq increases |
Parallel combination of capacitors can be identified by their common connection to the same two nodes, whereas in series, they are chained one after another between source and load.
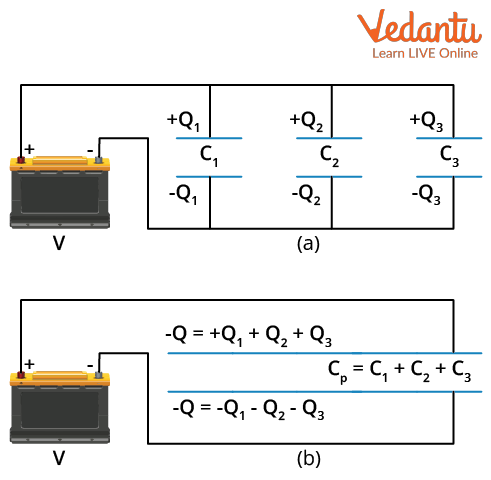
Formulas, Derivations, and How to Find Equivalent Capacitance
Knowing the right formula is vital for quickly determining the net capacitance in JEE problems. Below are the must-remember equations and a quick derivation for each arrangement.
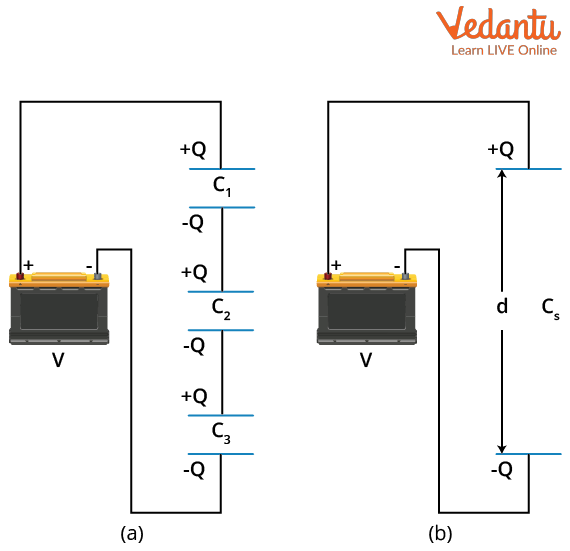
- Series Combination: 1/Ceq = 1/C1 + 1/C2 + ... + 1/Cn
- Parallel Combination: Ceq = C1 + C2 + ... + Cn
Derivation (Series): In series, charge Q is same across all capacitors, but voltage divides. By applying Kirchhoff’s law:
V = V1 + V2 + … ⇒ V = Q/C1 + Q/C2 + …
Hence, Q/Ceq = Q/C1 + Q/C2 + ... ⇒ 1/Ceq = 1/C1 + 1/C2 + ...
In parallel, voltage V is same, but charge divides. Q = Q1 + Q2 + ... = C1V + C2V + ... ⇒ Q = (C1 + C2 + ...)V. Therefore, Ceq = C1 + C2 + ...
Problem-Solving Steps and Common Pitfalls in Combination Of Capacitors
To crack capacitor networks in JEE, always identify which components are in true series or parallel (avoid mislabelling mixed groupings). Rearrange complex diagrams using node labelling and redraw if needed. Calculation mistakes often come from inverting or summing values in the wrong combination.
- Combine obvious series or parallel groups first, then reduce step-by-step.
- In series, smallest C dominates; in parallel, largest C dominates.
- Always use SI units (Farads); convert µF, nF to F early.
- Check for disconnected (open) branches—such capacitors carry zero charge.
- Don’t confuse with resistor rules—series and parallel formulas for caps are inverted compared to resistors.
- Always use consistent sign conventions and double-check units.
For a deeper analogy, compare with resistor combinations. Practice regularly with mixed-circuit sketches and reduction techniques to build speed.
Solved Examples – Combination Of Capacitors Numericals
Let’s apply the above strategies to real exam-level problems. Always draw a neat circuit diagram, then break the network into simpler groups for calculations.
Example: Three capacitors rated 2 µF, 3 µF and 6 µF are connected in series. What is the equivalent capacitance?
- Given: C1 = 2 µF, C2 = 3 µF, C3 = 6 µF.
- Since in series: 1/Cs = 1/2 + 1/3 + 1/6 = (3 + 2 + 1) / 6 = 1
- So, Ceq = 1 µF (series combo gives lowest net value)
Practice more such problems on Vedantu or try JEE pattern sheets for rapid improvement. For tackling networks, reference the section on equivalent capacitance in mixed arrangements.
Applications, Tricks, and Related Physics Connections
Understanding Combination Of Capacitors is not only crucial for JEE but is also foundational in modern electronics, from smartphones and TVs to advanced communication equipment. This topic also links concepts from Electrostatics, electric fields, and potential difference. Energy storage and distribution—vital in circuits—is directly governed by how capacitors are grouped.
Common exam traps include swapping resistor and capacitor formulas, mislabeling complex junctions, or skipping unit conversions. Always annotate diagrams and cross-check reduction steps to avoid costly errors in competitive exams.
For deeper revision, see differences between capacitor arrangements, explore stepwise breakdowns of mixed networks and attempt practice questions from the Vedantu JEE modules.
- Review properties of common capacitor types.
- Connect concepts to charging and discharging behaviour in RC circuits.
- Explore mixed grouping analogies in spring combinations for analogous reasoning.
- For theoretical and numerical practice, check Vedantu’s solved question bank dedicated to JEE Main Physics.
Mastering the Combination Of Capacitors will boost your confidence and speed for both conceptual and numerical sections in JEE, while also giving you insight into key electric circuit principles useful in higher studies and technology careers.
FAQs on Combination of Capacitors Explained with Formulas and Examples
1. What is the combination of capacitors?
A combination of capacitors refers to connecting two or more capacitors together in a circuit, either in series or in parallel, to obtain a specific equivalent capacitance. The way capacitors are combined affects the total capacitance and how voltage is distributed across each component.
2. What happens when capacitors are combined in series and in parallel?
When capacitors are combined in series, the total or equivalent capacitance decreases and is always less than the smallest individual capacitance. In parallel combinations, the total capacitance increases and is the sum of all individual capacitances. This impacts how much charge and voltage each capacitor can hold in a circuit:
- Series: Lower total capacitance; same charge on each capacitor
- Parallel: Higher total capacitance; same voltage across each capacitor
3. How do you calculate equivalent capacitance for different combinations?
To find the equivalent capacitance, use different formulas based on the arrangement:
- For series: 1/Ceq = 1/C1 + 1/C2 + 1/C3 + ...
- For parallel: Ceq = C1 + C2 + C3 + ...
4. Can you combine capacitors of different ratings?
Yes, capacitors of different capacitance values and voltage ratings can be combined in series or parallel. When doing so:
- The resulting equivalent capacitance is affected by both the arrangement and individual values.
- Always ensure no individual capacitor exceeds its rated voltage, especially in series circuits.
5. What are common combination questions asked in JEE Main?
Common JEE Main questions on this topic involve:
- Finding the equivalent capacitance of mixed series and parallel networks
- Calculating charge or voltage on specific capacitors in a circuit
- Deriving formulas for complicated arrangements
- Identifying energy stored in combined capacitors
- Spotting and reducing complex capacitor circuits accurately
6. What is the difference between series and parallel connection of capacitors?
The main difference lies in how capacitors share voltage and charge:
- Series combination: Same charge on each capacitor; voltages add up; equivalent capacitance is less than all individual values.
- Parallel combination: Same voltage across each; charges add up; equivalent capacitance is the sum of all capacitances.
7. How do I approach solving numerical problems on combination of capacitors?
To solve numerical problems on capacitor combinations:
- Redraw the circuit and identify series and parallel groups.
- Apply appropriate formulas stepwise to reduce the network.
- Use the logic: Series for decreasing capacitance, parallel for increasing.
- Check units and final answers, and be careful with voltage ratings.
8. Why can’t we directly add capacitances in series like resistors?
Unlike resistors, capacitances in series do not simply add because the charge across each capacitor is the same, but the potential difference divides among them. This leads to the reciprocal addition formula:
1/Ceq = 1/C1 + 1/C2 + ...
9. How does energy storage differ for series and parallel combinations?
Energy storage differs because total capacitance changes:
- Parallel: More energy stored (larger equivalent capacitance)
- Series: Less energy stored for same applied voltage
10. What are the practical applications of capacitor combinations in circuits?
Capacitor combinations are widely used to tailor circuit performance, such as filtering signals, tuning radios, energy storage in flash units, voltage smoothing in power supplies, and more. Series and parallel arrangements allow for designing circuits with specific time constants and voltage ratings.
11. What errors do students often make in circuit reduction for capacitors?
Common mistakes in circuit reduction with capacitors include:
- Confusing series and parallel arrangements
- Missing hidden series/parallel groups in complex diagrams
- Neglecting capacitor voltage ratings
- Inaccurate calculation of reciprocals for series combinations
12. Is polarity important when combining capacitors?
Polarity is important if you are dealing with electrolytic capacitors. Always connect such capacitors observing the indicated positive and negative terminals, especially in series, to prevent damage or failure. For non-polarized capacitors, orientation doesn't matter.


































