
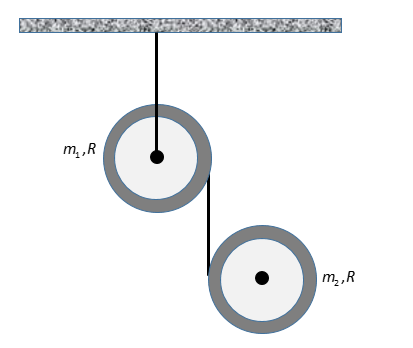
Linear acceleration of mass \[{m_2}\]is \[{a_2}\], then angular acceleration of \[{\alpha _1}\]is (given that there is no slipping).
A. \[\dfrac{{{a_2}}}{R}\]
B. \[\dfrac{{\left( {{a_2} + g} \right)}}{R}\]
C. \[\dfrac{{2\left( {{a_2} + g} \right)}}{R}\]
D. None of these
Answer
180k+ views
Hint: For no slipping condition or pure rotation condition the surface in contact is at instantaneous rest, i.e. the net force acting at that point is zero and hence there is no relative acceleration of the point.
Complete step by step solution:
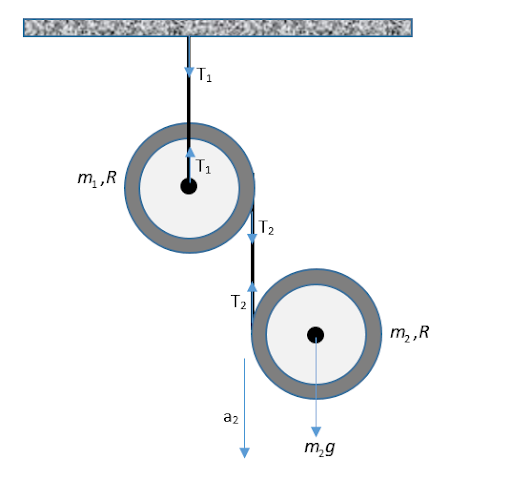
Image: Two rings joined by common string
Let the tension in the string connected with mass \[{m_1}\] is \[{T_1}\] and the tension in the string connecting both the masses is \[{T_2}\]. \[{\alpha _1}\] is the acceleration of the mass \[{m_1}\], \[{a_2}\] is the linear acceleration of the mass \[{m_2}\] and \[{\alpha _2}\] is the angular acceleration of the mass \[{m_2}\].
For mass \[{m_2}\] writing the Newton’s 2nd law of motion,
\[\begin{array}{c}{F_{net}} = ma\\ \Rightarrow {m_2}g - {T_2} = {m_2}{a_2} \ldots \ldots \left( i \right)\end{array}\]
The moment of inertia of the circular ring about its centre of mass is given as,
\[I = M{R^2}\]
Here, \[M\] is the mass and \[R\] is the radius of the ring.
So,
\[\begin{array}{c}{I_1} = {m_1}{R^2}\\{I_2} = {m_2}{R^2}\end{array}\]
Net torque acting about the centre of mass \[{m_2}\] is \[{T_2}R\] and the direction is clockwise. For no slipping condition,
\[{a_2} = {\alpha _2}R\]
So, the angular acceleration will be,
\[{\alpha _2} = \dfrac{{{a_2}}}{R}\]
For mass\[{m_1}\],
Using no slipping condition,
\[{c}{\alpha _1} = {\alpha _2}\]
\[\therefore {\alpha _1}= \dfrac{{{a_2}}}{R}\]
Therefore, the correct option is A.
Note: We need to assume that the string connecting both the rings are massless and inextensible. If the string is not massless and inextensible then the tension at the point of contact will be different for both the rings. If the motion is not purely rolling/slipping then we can’t use the used relation between the angular acceleration and the linear acceleration for both the rings. The linear acceleration of mass \[{m_1}\] should be zero as its centre is attached to an inextensible and immovable string.
Complete step by step solution:

Image: Two rings joined by common string
Let the tension in the string connected with mass \[{m_1}\] is \[{T_1}\] and the tension in the string connecting both the masses is \[{T_2}\]. \[{\alpha _1}\] is the acceleration of the mass \[{m_1}\], \[{a_2}\] is the linear acceleration of the mass \[{m_2}\] and \[{\alpha _2}\] is the angular acceleration of the mass \[{m_2}\].
For mass \[{m_2}\] writing the Newton’s 2nd law of motion,
\[\begin{array}{c}{F_{net}} = ma\\ \Rightarrow {m_2}g - {T_2} = {m_2}{a_2} \ldots \ldots \left( i \right)\end{array}\]
The moment of inertia of the circular ring about its centre of mass is given as,
\[I = M{R^2}\]
Here, \[M\] is the mass and \[R\] is the radius of the ring.
So,
\[\begin{array}{c}{I_1} = {m_1}{R^2}\\{I_2} = {m_2}{R^2}\end{array}\]
Net torque acting about the centre of mass \[{m_2}\] is \[{T_2}R\] and the direction is clockwise. For no slipping condition,
\[{a_2} = {\alpha _2}R\]
So, the angular acceleration will be,
\[{\alpha _2} = \dfrac{{{a_2}}}{R}\]
For mass\[{m_1}\],
Using no slipping condition,
\[{c}{\alpha _1} = {\alpha _2}\]
\[\therefore {\alpha _1}= \dfrac{{{a_2}}}{R}\]
Therefore, the correct option is A.
Note: We need to assume that the string connecting both the rings are massless and inextensible. If the string is not massless and inextensible then the tension at the point of contact will be different for both the rings. If the motion is not purely rolling/slipping then we can’t use the used relation between the angular acceleration and the linear acceleration for both the rings. The linear acceleration of mass \[{m_1}\] should be zero as its centre is attached to an inextensible and immovable string.
Recently Updated Pages
Class 11 JEE Main Physics Mock Test - FREE Online Mock Test Series 2025

Degree of Dissociation Important Concepts and Tips for JEE

Learn Conversion of Galvanometer into Ammeter and Voltmeter for JEE Main

JEE Main Chemistry Question Paper PDF Download with Answer Key

Electric Field Due To Uniformly Charged Ring - JEE Main 2025

JEE Electricity and Magnetism Important Concepts and Tips for Exam Preparation

Trending doubts
JEE Main 2025 Session 2: Application Form (Out), Exam Dates (Released), Eligibility, & More

JEE Main 2025: Derivation of Equation of Trajectory in Physics

Displacement-Time Graph and Velocity-Time Graph for JEE

Atomic Structure - Electrons, Protons, Neutrons and Atomic Models

Learn About Angle Of Deviation In Prism: JEE Main Physics 2025

What is Hybridisation in Chemistry?

Other Pages
NCERT Solutions For Class 11 Physics Chapter 2 Motion In A Straight Line - 2025-26

NCERT Solutions For Class 11 Physics Chapter 1 Units and Measurements - 2025-26

NCERT Solutions For Class 11 Physics Chapter 3 Motion In A Plane - 2025-26

JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Units And Measurements Class 11 Physics Chapter 1 CBSE Notes - 2025-26

Motion in a Straight Line Class 11 Physics Chapter 2 CBSE Notes - 2025-26




