
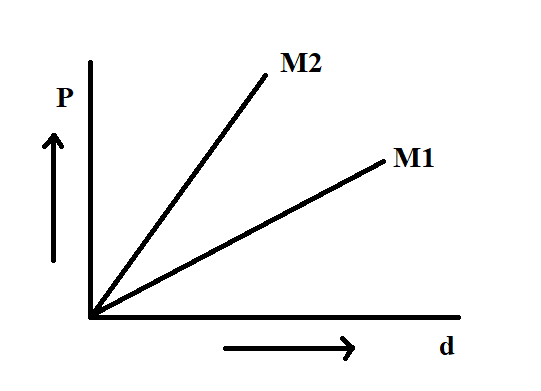
In the Boyle's law experiment, the graph drawn between pressure and density for a given temperature of different gases are the straight lines then the molecular weights have the relation
A) ${M_1} > {M_2}$
B) ${M_2} > {M_1}$
C) ${M_1} = {M_2}$
D) $M_2^2 = {M_1}$
Answer
173.4k+ views
Hint: The graph is between pressure and density. To find the relation between the two masses can be obtained by using the expression for density and Boyle's law for an ideal gas. The density of a gas is the ratio of its mass to the volume. Boyle's law graphs are plotted with pressure on one axis and reciprocal of volume on the other axis. In this graph mass of the gas is multiplied by the volume to get density on the x-axis.
Formula used:
$d = \dfrac{m}{V}$ (Where d stands for the density, m stands for the given mass and V stands for the volume)
The ideal gas equation is given by,
$PV = nRT$ (where P is the pressure of the gas, V is the volume of the gas, n stands for the number of moles, R stands for the universal gas constant and T is the temperature of the gas)
Complete step by step solution:
We know that in the graph, pressure versus density is shown,
We know the expression for density,
Density $d = $$\dfrac{{mass}}{{volume}} = \dfrac{m}{V}$
Boyle's law for ideal gases is given by,
$PV = nRT$
$n$ is the number of moles which is given by, $\dfrac{{mass(given)}}{{Mass(molecular)}} = \dfrac{m}{M}$
where$ M$ is the molecular weight.
Substituting the value of $n$ in the ideal gas equation,
$PV = \dfrac{m}{M}RT$
Rearranging this equation, we get the density
Density, $(d)= \dfrac{m}{V} = \dfrac{{PM}}{{RT}}$
The graph of pressure versus density is shown in the figure as a straight line.
From the equation, we get that the slope of this line is, $\dfrac{{RT}}{M}$
As the molecular mass is in the denominator, the line with a greater slope will be having less molecular mass.
Since ${M_2}$ is steeper than ${M_1}$, ${M_1}$ will be greater than ${M_2}$.
Hence, the answer is (A), ${M_1} > {M_2}$.
Note: The slope will be more for a steeper line. Boyle’s law states that for a constant temperature the volume of a given mass of a gas is inversely proportional to volume. Gases are liquefied by using the principle of Boyle’s law. Boyle's law has many real-life applications also. The injection syringe is one example of Boyle's law.
Formula used:
$d = \dfrac{m}{V}$ (Where d stands for the density, m stands for the given mass and V stands for the volume)
The ideal gas equation is given by,
$PV = nRT$ (where P is the pressure of the gas, V is the volume of the gas, n stands for the number of moles, R stands for the universal gas constant and T is the temperature of the gas)
Complete step by step solution:
We know that in the graph, pressure versus density is shown,
We know the expression for density,
Density $d = $$\dfrac{{mass}}{{volume}} = \dfrac{m}{V}$
Boyle's law for ideal gases is given by,
$PV = nRT$
$n$ is the number of moles which is given by, $\dfrac{{mass(given)}}{{Mass(molecular)}} = \dfrac{m}{M}$
where$ M$ is the molecular weight.
Substituting the value of $n$ in the ideal gas equation,
$PV = \dfrac{m}{M}RT$
Rearranging this equation, we get the density
Density, $(d)= \dfrac{m}{V} = \dfrac{{PM}}{{RT}}$
The graph of pressure versus density is shown in the figure as a straight line.
From the equation, we get that the slope of this line is, $\dfrac{{RT}}{M}$
As the molecular mass is in the denominator, the line with a greater slope will be having less molecular mass.
Since ${M_2}$ is steeper than ${M_1}$, ${M_1}$ will be greater than ${M_2}$.
Hence, the answer is (A), ${M_1} > {M_2}$.
Note: The slope will be more for a steeper line. Boyle’s law states that for a constant temperature the volume of a given mass of a gas is inversely proportional to volume. Gases are liquefied by using the principle of Boyle’s law. Boyle's law has many real-life applications also. The injection syringe is one example of Boyle's law.
Recently Updated Pages
Sets, Relations, and Functions Mock Test 2025-26

JEE Main Mock Test 2025-26: Purification & Characterisation of Organic Compounds

JEE Main 2025 Coordination Compounds Mock Test – Free Practice Online

JEE Main 2025-26 Equilibrium Mock Test: Free Practice Online

JEE Main Mock Test 2025-26: D and F Block Elements Practice

JEE Main Mock Test 2025-26: Chapter-Wise Practice Papers

Trending doubts
JEE Main 2025 Session 2: Application Form (Out), Exam Dates (Released), Eligibility, & More

Displacement-Time Graph and Velocity-Time Graph for JEE

Uniform Acceleration

JEE Main 2025: Derivation of Equation of Trajectory in Physics

Learn About Angle Of Deviation In Prism: JEE Main Physics 2025

Instantaneous Velocity - Formula based Examples for JEE

Other Pages
NCERT Solutions For Class 11 Physics Chapter 1 Units and Measurements - 2025-26

NCERT Solutions For Class 11 Physics Chapter 2 Motion In A Straight Line - 2025-26

JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Units And Measurements Class 11 Physics Chapter 1 CBSE Notes - 2025-26

NCERT Solutions For Class 11 Physics Chapter 3 Motion In A Plane - 2025-26

Motion in a Straight Line Class 11 Physics Chapter 2 CBSE Notes - 2025-26




