
A wire frame in the shape of an equilateral triangle is hinged at one vertex so that it can swing freely in a vertical plane, with the plane of the triangle always remaining vertical. The side of the frame is $\dfrac{1}{{\sqrt 3 }}$ m. The time period in seconds of small oscillations of the frame will be (g=10 m${s^{ - 2}}$ )
A) $\dfrac{\pi }{{\sqrt 2 }}$
B) $\dfrac{\pi }{{\sqrt 3 }}$
C) $\dfrac{\pi }{{\sqrt 6 }}$
D) $\dfrac{\pi }{{\sqrt 5 }}$
Answer
146.4k+ views
Hint: In order to solve the question, we need to find out the moment of inertia of the triangle side by side and then adding them together. The formula for time period of oscillation is period T=$2\pi \sqrt {\dfrac{I}{{mgL}}} $ where, I is the moment of inertia, m is the mass, g is the gravity (g=10 m${s^{ - 2}}$ ), and L is the distance from center of mass to the point of hinging will help in finding the solution.
Complete step by step answer:
Step 1:
Before we start we need to look into the definition of some quantity which we are going to use in solving the question.
Oscillation refers to any Periodic Motion moving at a distance about the equilibrium position and repeats itself over and over for a period of time. Example The Oscillation up and down of a spring, The Oscillation side by side of a spring. The Oscillation swinging side by side of a pendulum
Moment of inertia: In physics, quantitative measure of the rotational inertia of a bodyi.e., the opposition that the body exhibits to having its speed of rotation about an axis altered by the application of a torque (turning force). The axis may be internal or external and may or may not be fixed.
Parallel Axis Theorem: The moment of inertia of a body about any axis is equal to the sum of the moment of inertia of the body about a parallel axis passing through its centre of mass and the product of its mass and the square of the distance between the two parallel axes.
Step 2:
Coming to the question:
We are given that a wire frame in the shape of an equilateral triangle is hinged at one vertex so that it can swing freely in a vertical plane, with the plane of the triangle always remaining vertical. The side of the frame is $\dfrac{1}{{\sqrt 3 }}$ m
Here we have a diagram for clear understanding.
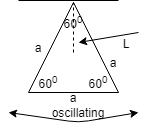
Here a is the side of the triangle and L is the distance from center of mass to the point of hinging which is equal to $\dfrac{a}{{\sqrt 3 }}$
First we will find out the moment of inertia, I
Let the mass of the triangle be m, so each side will have mass $\dfrac{m}{3}$
Now we are using moment of inertia on all the sides. The side at the base will have a moment of inertia of $\dfrac{{{a^2}}}{{12}}$ and also we have to apply parallel axis theorem because of the side and the hinged place.
Then I=$\dfrac{m}{3}$$\left( {\dfrac{{{a^2}}}{3} + \dfrac{{{a^2}}}{3} + \dfrac{{{a^2}}}{{12}} + {{\left( {\dfrac{{\sqrt {3a} }}{2}} \right)}^2}} \right)$
Solving for I, $\dfrac{{2m{a^2}}}{9} + \dfrac{{m{a^2}}}{{36}} + \dfrac{{m{a^2}}}{4}$ which is equal to $\dfrac{1}{2}m{a^2}$ ……… (1)
We are asked for the time period, now using the formula for time period T=$2\pi \sqrt {\dfrac{I}{{mgL}}} $ where, I is the moment of inertia, m is the mass, g is the gravity (g=10 m${s^{ - 2}}$ ), and L is the distance from center of mass to the point of hinging.
Substituting the value in time period we get, T=$2\pi \sqrt {\dfrac{{\dfrac{1}{2}m{a^2}}}{{mg\dfrac{a}{{\sqrt 3 }}}}} $
On further solving the term and cancelling the common term we get, T=$2\pi \sqrt {\dfrac{1}{{2g}}} $
Putting the value of g=10 m${s^{ - 2}}$ we get T = $\dfrac{\pi }{{\sqrt 5 }}$
Therefore the correct option is D.
Note: The combined moment of inertia is obtained using parallel axis theorem in finding the moment of inertia which states that moment of any axis parallel to the original axis is sum of the moment of inertia about the original axis and product of mass times distance between the axes squared.
Complete step by step answer:
Step 1:
Before we start we need to look into the definition of some quantity which we are going to use in solving the question.
Oscillation refers to any Periodic Motion moving at a distance about the equilibrium position and repeats itself over and over for a period of time. Example The Oscillation up and down of a spring, The Oscillation side by side of a spring. The Oscillation swinging side by side of a pendulum
Moment of inertia: In physics, quantitative measure of the rotational inertia of a bodyi.e., the opposition that the body exhibits to having its speed of rotation about an axis altered by the application of a torque (turning force). The axis may be internal or external and may or may not be fixed.
Parallel Axis Theorem: The moment of inertia of a body about any axis is equal to the sum of the moment of inertia of the body about a parallel axis passing through its centre of mass and the product of its mass and the square of the distance between the two parallel axes.
Step 2:
Coming to the question:
We are given that a wire frame in the shape of an equilateral triangle is hinged at one vertex so that it can swing freely in a vertical plane, with the plane of the triangle always remaining vertical. The side of the frame is $\dfrac{1}{{\sqrt 3 }}$ m
Here we have a diagram for clear understanding.

Here a is the side of the triangle and L is the distance from center of mass to the point of hinging which is equal to $\dfrac{a}{{\sqrt 3 }}$
First we will find out the moment of inertia, I
Let the mass of the triangle be m, so each side will have mass $\dfrac{m}{3}$
Now we are using moment of inertia on all the sides. The side at the base will have a moment of inertia of $\dfrac{{{a^2}}}{{12}}$ and also we have to apply parallel axis theorem because of the side and the hinged place.
Then I=$\dfrac{m}{3}$$\left( {\dfrac{{{a^2}}}{3} + \dfrac{{{a^2}}}{3} + \dfrac{{{a^2}}}{{12}} + {{\left( {\dfrac{{\sqrt {3a} }}{2}} \right)}^2}} \right)$
Solving for I, $\dfrac{{2m{a^2}}}{9} + \dfrac{{m{a^2}}}{{36}} + \dfrac{{m{a^2}}}{4}$ which is equal to $\dfrac{1}{2}m{a^2}$ ……… (1)
We are asked for the time period, now using the formula for time period T=$2\pi \sqrt {\dfrac{I}{{mgL}}} $ where, I is the moment of inertia, m is the mass, g is the gravity (g=10 m${s^{ - 2}}$ ), and L is the distance from center of mass to the point of hinging.
Substituting the value in time period we get, T=$2\pi \sqrt {\dfrac{{\dfrac{1}{2}m{a^2}}}{{mg\dfrac{a}{{\sqrt 3 }}}}} $
On further solving the term and cancelling the common term we get, T=$2\pi \sqrt {\dfrac{1}{{2g}}} $
Putting the value of g=10 m${s^{ - 2}}$ we get T = $\dfrac{\pi }{{\sqrt 5 }}$
Therefore the correct option is D.
Note: The combined moment of inertia is obtained using parallel axis theorem in finding the moment of inertia which states that moment of any axis parallel to the original axis is sum of the moment of inertia about the original axis and product of mass times distance between the axes squared.
Recently Updated Pages
How to find Oxidation Number - Important Concepts for JEE

How Electromagnetic Waves are Formed - Important Concepts for JEE

Electrical Resistance - Important Concepts and Tips for JEE

Average Atomic Mass - Important Concepts and Tips for JEE

Chemical Equation - Important Concepts and Tips for JEE

Concept of CP and CV of Gas - Important Concepts and Tips for JEE

Trending doubts
JEE Main 2025 Session 2: Application Form (Out), Exam Dates (Released), Eligibility, & More

JEE Main Exam Marking Scheme: Detailed Breakdown of Marks and Negative Marking

JEE Main 2025: Derivation of Equation of Trajectory in Physics

Electric Field Due to Uniformly Charged Ring for JEE Main 2025 - Formula and Derivation

JEE Main Participating Colleges 2024 - A Complete List of Top Colleges

Degree of Dissociation and Its Formula With Solved Example for JEE

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

JEE Advanced 2025: Dates, Registration, Syllabus, Eligibility Criteria and More

Units and Measurements Class 11 Notes: CBSE Physics Chapter 1

NCERT Solutions for Class 11 Physics Chapter 1 Units and Measurements

Motion in a Straight Line Class 11 Notes: CBSE Physics Chapter 2

JEE Advanced Weightage 2025 Chapter-Wise for Physics, Maths and Chemistry




