Lines and Angles Class 7 Extra Questions and Answers Free PDF Download
FAQs on CBSE Important Questions for Class 7 Maths Lines and Angles - 2025-26
1. What are the most important topics in CBSE Class 7 Maths Chapter 5, Lines and Angles, for the 2025-26 exams?
For the Class 7 exams, the most frequently tested topics from Lines and Angles are:
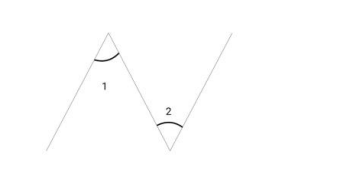
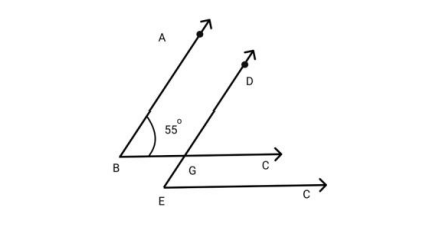
- Properties of angles formed when a transversal intersects two parallel lines (alternate interior, corresponding, and co-interior angles).
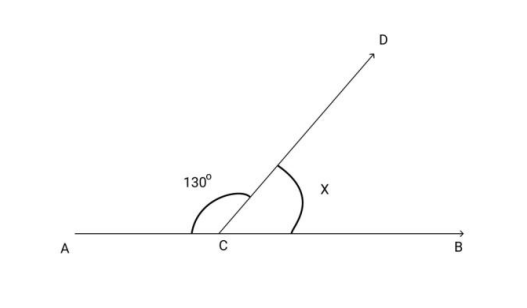
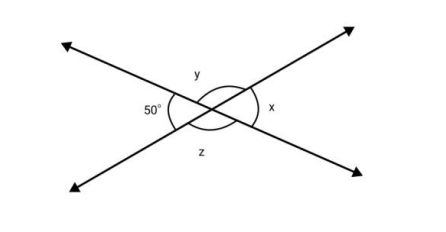
- Solving for unknown angles using the properties of linear pairs and vertically opposite angles.
- Identifying and calculating complementary and supplementary angles.
2. How do I solve exam questions where a transversal intersects two parallel lines?
First, carefully identify the relationship between the given angle and the unknown angle in the diagram. Determine if they are corresponding angles (which are equal), alternate interior angles (also equal), or consecutive interior angles (their sum is 180°). Use the correct property to set up an equation and solve for the unknown value. For full marks, always state the geometric reason for each step in your answer.
3. What is a common mistake students make in Lines and Angles problems?
A very common error is confusing adjacent angles with a linear pair. While all angles in a linear pair are adjacent, not all adjacent angles form a linear pair. A linear pair must have non-common arms that are opposite rays, and their sum must be exactly 180°. Mistaking any two adjacent angles as supplementary can lead to incorrect calculations in exam problems.
4. From an exam perspective, why is understanding the properties of a transversal so important?
Understanding transversal properties is crucial because they are fundamental to solving most geometry problems in Class 7 and beyond. Exam questions often test logical reasoning by combining these properties. For example, you might need to use the alternate interior angles property to find one angle and then apply the linear pair property to find another angle within the same figure. This skill is essential for multi-step problems.
5. What type of question can I expect for 3 marks from the Lines and Angles chapter?
A typical 3-mark question will present a diagram with two parallel lines cut by one or more transversals, involving several unknown angles (e.g., labeled x, y, and z). You will be expected to find the value of each angle by applying a sequence of properties, such as vertically opposite angles, corresponding angles, and linear pairs, providing a clear reason for each calculation.
6. How is the concept of supplementary angles applied to problems involving parallel lines?
The concept of supplementary angles (two angles adding up to 180°) is directly applied in the property of consecutive interior angles. When a transversal intersects two parallel lines, the pair of interior angles on the same side of the transversal are always supplementary. This is a key relationship frequently used in exams to find an unknown angle or to prove if two given lines are parallel.
7. How do you prove if two lines are parallel using angle properties in an exam?
To prove that two lines are parallel, you must use the converse of the transversal angle properties. You need to show that one of the following conditions is met:
- A pair of corresponding angles are equal.
- A pair of alternate interior angles are equal.
- A pair of consecutive interior angles are supplementary (their sum is 180°).
8. What is the difference between adjacent angles and vertically opposite angles?
Adjacent angles share a common vertex and a common arm, but have no common interior points. They lie next to each other. In contrast, vertically opposite angles are formed when two lines intersect, and they are opposite to each other. While adjacent angles can have any sum, vertically opposite angles are always equal to each other. This property is vital for solving equations in geometry.