Electromagnetic Induction Class 12 important questions with answers PDF download



FAQs on CBSE Important Questions for Class 12 Physics Electromagnetic Induction - 2025-26
1. What are the most important topics in Chapter 6, Electromagnetic Induction, for the CBSE Class 12 Board Exam 2025-26?
For the Class 12 Board Exam, the most crucial topics in Electromagnetic Induction are:
- Faraday's Laws and Lenz's Law: These form the conceptual backbone and are often tested in 1 or 2-mark questions.
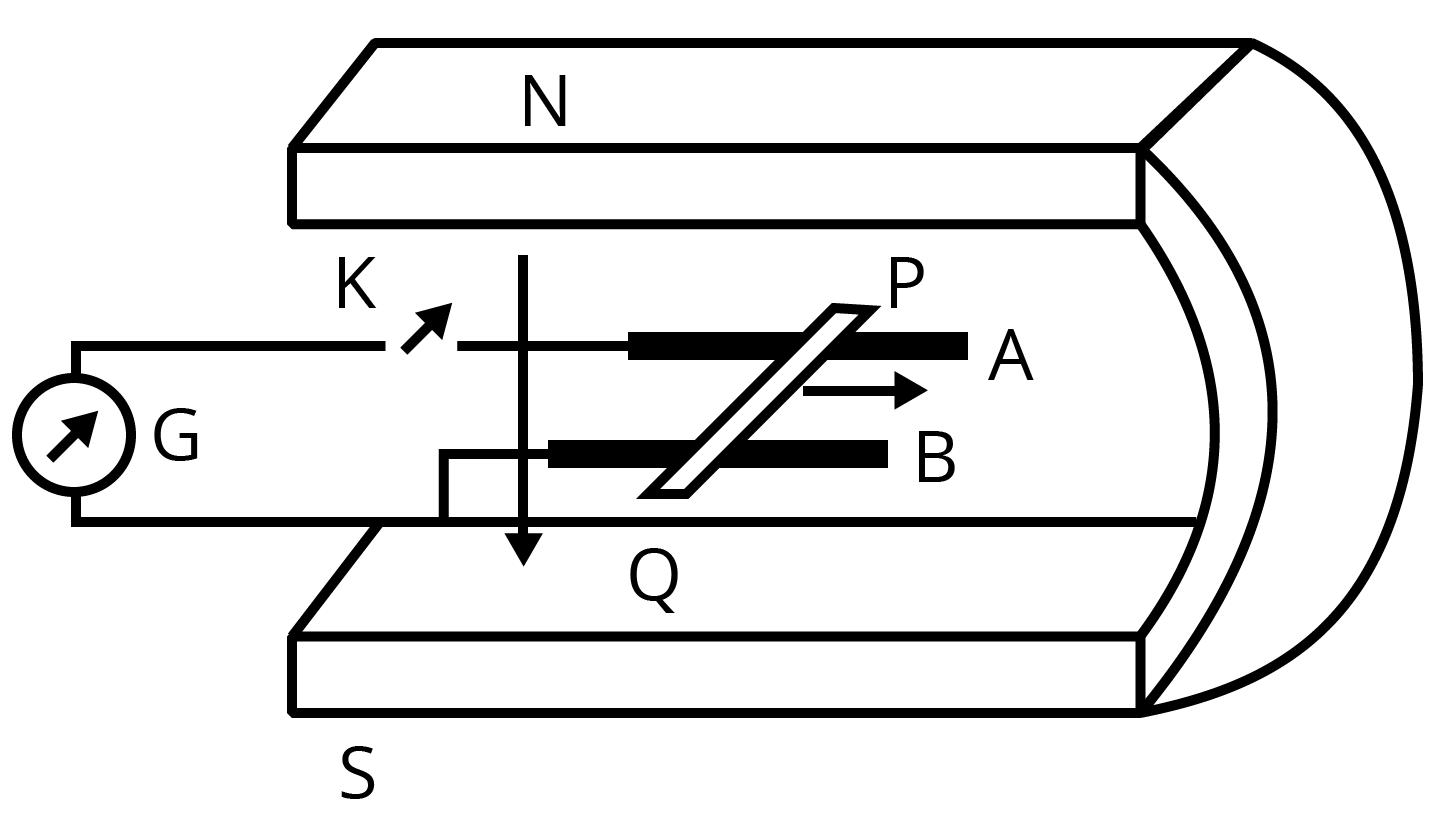
- Motional EMF: Derivations and numerical problems on EMF induced in moving conductors are very common.
- Self and Mutual Inductance: Expect definitions, S.I. units, and numericals. The derivation for the self-inductance of a solenoid is a frequent 3-mark question.
- AC Generator: The principle, construction, and working, along with the derivation of the induced EMF, is a potential 5-mark question.
- Eddy Currents: Conceptual questions on its applications and disadvantages are often asked.
2. How should I use these important questions for Chapter 6 to score well in my Physics exam?
To maximise your score using these questions, follow a strategic approach:
- Test Your Concepts: Start with the 1-mark and 2-mark questions to quickly check if your understanding of fundamental concepts like Lenz's Law and magnetic flux is clear.
- Practice Numericals: Move to the 3-mark questions, which are often numericals. This helps in applying formulas for motional EMF, inductance, and transformers under exam-like conditions.
- Master Derivations: Dedicate focused time to the 5-mark questions, which typically include long derivations like that of an AC generator. Practice writing them step-by-step.
- Identify Weak Areas: Whichever question you find difficult, revisit that topic in your NCERT textbook immediately.
3. Why is Lenz's Law considered a consequence of the law of conservation of energy?
Lenz's Law states that the direction of induced current is always such that it opposes the change in magnetic flux that produced it. This opposition is a direct manifestation of the law of conservation of energy. If the induced current were to aid the change, it would create a bigger change, leading to a larger current, and so on. This would create energy from nothing, which is impossible. Therefore, to induce a current, mechanical work must be done against the opposing force, and this work is converted into electrical energy, upholding the principle of energy conservation.
4. What types of numerical problems are frequently asked from Electromagnetic Induction?
Based on previous board paper trends, you can expect numericals based on the following formulas:
- Calculating induced EMF in a straight conductor moving in a magnetic field (e = Blv).
- Calculating induced EMF in a rotating coil or rod (e = 1/2 BωR²).
- Problems on self-inductance (L) and mutual inductance (M), often involving solenoids.
- Calculating flux change and induced EMF using Faraday's Law (ε = -dΦ/dt).
- Calculations related to transformers, including transformation ratio (K), efficiency, and current/voltage in primary and secondary coils.
5. A metallic piece gets hot when placed in a high-frequency AC field, but not in a steady magnetic field. Why is this an important concept for board exams?
This phenomenon is due to eddy currents. A steady magnetic field (like from a DC source) does not cause a change in magnetic flux, so no current is induced. However, a high-frequency AC field creates a rapidly changing magnetic flux. This induces large, circulating currents (eddy currents) within the metallic piece. Due to the metal's resistance, this large current produces significant heat (Joule's heating effect). This concept is important for exams as it tests the core principle that induction requires a change in flux and has practical applications like induction furnaces and electromagnetic brakes, which are often asked as 1 or 2-mark conceptual questions.
6. Which derivations from Chapter 6 are essential for scoring full marks in a 5-mark question?
For the 5-mark section, mastering the following derivations from Electromagnetic Induction is crucial:
- Expression for the induced EMF in a rotating coil in a uniform magnetic field, which is the principle of an AC Generator.
- Expression for the self-inductance of a long solenoid.
- Expression for the mutual inductance of a pair of co-axial solenoids.
- Derivation for the EMF induced in a conducting rod rotating in a uniform magnetic field.
Always draw a neat, labelled diagram with your derivation to score full marks.
7. What is the key difference between self-inductance and mutual-inductance, and how is this difference tested in exams?
The key difference lies in the source of the magnetic flux change:
- Self-Inductance (L) is the property of a single coil to oppose a change in the current flowing *through itself*. The changing flux is produced by the coil's own current.
- Mutual-Inductance (M) is the property of a pair of coils where a change in current in one coil induces an EMF in the *other* coil.
In exams, this is tested through:
- Definitions and Units: 1-mark questions asking to define the terms and their S.I. unit (Henry).
- Conceptual Questions: Asking for factors affecting L and M.
- Numerical Problems: You must identify from the problem statement whether it involves a single coil (use L) or two coils (use M).
8. What kind of 1-mark or MCQ-type questions can I expect from the topic of transformers?
For 1-mark or MCQ questions on transformers, be prepared for:
- Principle: The working principle of a transformer is mutual induction.
- Transformation Ratio (K): Simple calculations using K = Ns/Np = Vs/Vp.
- Ideal Transformer: The condition for an ideal transformer (efficiency is 100%, no power loss) and the relation IpVp = IsVs.
- Identification: Identifying a transformer as step-up (Ns > Np) or step-down (Np > Ns).
- Core Type: Why a soft iron core is used (to concentrate magnetic flux).
9. Why is the concept of 'back EMF' in an inductor crucial for understanding circuits, and how might it appear as a HOTS question?
Back EMF is the self-induced EMF in an inductor that opposes any change in the current flowing through it. It's crucial because it gives the inductor its property of electrical inertia, resisting sudden changes in current. A common Higher Order Thinking Skills (HOTS) question based on this is: "Explain why a large spark is observed at the switch when a circuit with a large inductor is suddenly switched off." The answer is that when the circuit is broken, the current collapses rapidly. The inductor generates a very large back EMF to oppose this change, which can be high enough to ionise the air across the switch gap, causing a visible spark.
10. Is it sufficient to only practice these important questions for Chapter 6?
While these important questions are excellent for understanding the CBSE exam pattern, identifying high-weightage topics, and targeted practice, they should not be your only resource. For a complete preparation:
- First, build a strong conceptual foundation by thoroughly studying the NCERT textbook.
- Then, use this list of important questions to test your knowledge, practice application, and master the art of writing answers as per the board's expectations.
- Combining NCERT with these questions ensures both deep understanding and exam-readiness.