Important Questions for CBSE Class 10 Maths Chapter 2 - Polynomials 2024-25

Very Short Answer Questions (1 Mark)

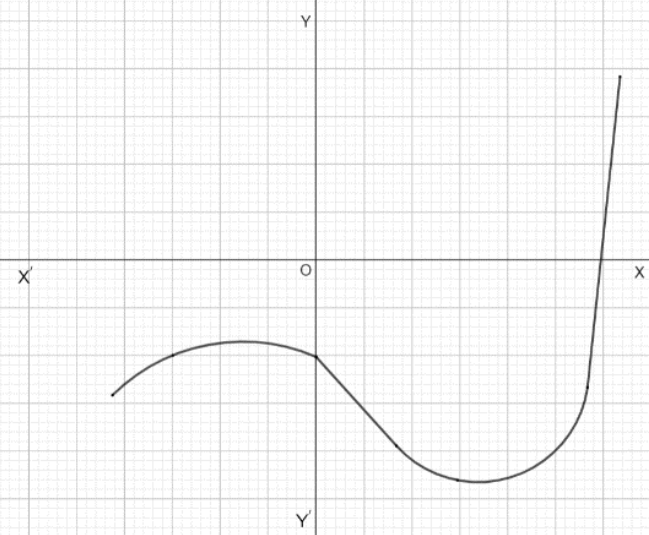
1. The graphs of $y=p(x)$ are given to us, for some polynomials $p(x)$. Find the number of zeroes of $p(x)$, in each case.

i.

Ans: The graph does not meet the $x-$ axis at any point. Hence, it does not have any zero.

ii.

Ans: The graph meets the $x-$ axis at only $1$ point. Thus, the polynomial $p(x)$ corresponding to the given graph has only $1$ zero.

iii.

Ans: The graph meets the $x-$ axis at $3$ points. Thus, the polynomial $p(x)$ corresponding to the given graph has $3$ zeroes.

iv.

Ans: The graph meets the $x-$ axis at $2$ points. Thus, the polynomial $p(x)$ corresponding to the given graph has $2$ zeroes.

v.

Ans: The graph meets the $x-$ axis at $3$ points. Thus, the polynomial $p(x)$ corresponding to the given graph has $3$ zeroes.

vi.

Ans: The graph meets the $x-$ axis at $4$ points. Thus, the polynomial $p(x)$ corresponding to the given graph has $4$ zeroes.

2. Which of the following is polynomial?

1. ${{x}^{2}}-6\sqrt{x}+2$  

2.  $\sqrt{x}+\dfrac{1}{\sqrt{x}}$ 

3. \[\dfrac{5}{{{x}^{2}}-3x+1}\] 

4. none of these 

Ans: d. none of these

3. Polynomial $2{{x}^{4}}+3{{x}^{3}}-5{{x}^{2}}-5{{x}^{2}}+9x+1$  is a

1. linear polynomial

2. quadratic polynomial

3. cubic polynomial

4. bi-quadratic polynomial

Ans: d. bi-quadratic polynomial

4. If $\alpha $ and $\beta $  are zeros of ${{x}^{2}}+5x+8$  , then the value of $(\alpha +\beta )$  is           

1. $5$

2. $-5$

3.  $8$

4. $-8$

Ans:  b. $-5$

5. The sum and product of the zeros of a quadratic polynomial are $2$  and $-15$ respectively. The quadratic polynomial is    

1. ${{x}^{2}}-2x+15$ 

2. ${{x}^{2}}-2x-15$ 

3. ${{x}^{2}}+2x+15$ 

4. ${{x}^{2}}+2x+15$ 

Ans: b. \[{{x}^{2}}-2x-15\]

6. If $p(x)=2{{x}^{2}}-3x+5$,$3x+5$ , then the value of $p(-1)$ is equal to                 

1. $7$ 

2. $8$ 

3. $9$ 

4. $10$ 

Ans: d. \[10\]

7. Zeros of $p(x)={{x}^{2}}-2x-3$     

1. $3$ and $1$ 

2. $3$ and $-1$ 

3. $-3$ and $-1$ 

4. $1$ and $-3$ 

Ans: b. \[3\] and \[-1\]

8. If $\alpha $ and $\beta $ are the zeros of $2{{x}^{2}}+5x-10$ , then the value of $\alpha \beta $ is     

1. $-\dfrac{5}{2}$ 

2.  $5$ 

3. $-5$ 

4.  $\dfrac{2}{5}$ 

Ans: c. \[-5\]

9. A quadratic polynomial, the sum and product of whose zeros are $0$ and $\sqrt{5}$                                     

1. ${{x}^{2}}+\sqrt{5}$ 

2. ${{x}^{2}}-\sqrt{5}$  

3. ${{x}^{2}}-5$ 

4. none of these

Ans: a. \[{{x}^{2}}+\sqrt{5}\]

10. Which of the following is polynomial?    

1. ${{x}^{2}}-6\sqrt{x}+2$  

2. $\sqrt{x}+\dfrac{1}{\sqrt{x}}$ 

3. \[\dfrac{5}{{{x}^{2}}-3x+1}\] 

4. none of these 

Ans: d. none of these

11. Polynomial $2{{x}^{4}}+3{{x}^{3}}-5{{x}^{2}}-5{{x}^{2}}+9x+1$ is a  

1. linear polynomial

2. quadratic polynomial

3. cubic polynomial

4. bi-quadratic polynomial

Ans: d. bi-quadratic polynomial

12. If $\alpha $ and $\beta $ are zeros of ${{x}^{2}}+5x+8$ , then the value of $\left( \alpha +\beta  \right)$ is   

1. $5$

2. $-5$

3. $8$

4. $-8$

Ans:  b. \[-5\]

13. The sum and product of the zeros of a quadratic polynomial are $2$  and $-15$ respectively. The quadratic polynomial is    

1. ${{x}^{2}}-2x+15$ 

2. ${{x}^{2}}-2x-15$ 

3. ${{x}^{2}}+2x+15$ 

4. ${{x}^{2}}+2x+15$ 

Ans: b. \[{{x}^{2}}-2x-15\]

Short Answer Questions                                                    (2 Marks)

1. Find the quadratic polynomial where sum and product of the zeros are $a$ and$\dfrac{1}{a}$.                           

Ans: A quadratic polynomial is given by: ${{x}^{2}}-$(sum of zeros)$x+$(product of zeros)

Given, the sum of zeros as $a$ and the product of zeros as $\dfrac{1}{a}$.

Thus, the quadratic polynomial is ${{x}^{2}}-ax+\dfrac{1}{a}$, i.e., $\dfrac{1}{a}\left[ a{{x}^{2}}-{{a}^{2}}x+1 \right]$.

2. If $\text{ }\!\!\alpha\!\!\text{ }$ and $\text{ }\!\!\beta\!\!\text{ }$ are the zeros of the quadratic polynomial $f(x)={{x}^{2}}-x-4$ , find the value of $\dfrac{\text{1}}{\text{ }\!\!\alpha\!\!\text{ }}\text{+}\dfrac{\text{1}}{\text{ }\!\!\beta\!\!\text{ }}\text{- }\; alpha \beta\!\!\text{ }$.

Ans: Given, $f(x)={{x}^{2}}-x-4$ and the zeros of the polynomial are $\alpha $ and $\beta $.

Therefore, the sum of the zeros,  $\text{ }\!\!\alpha\!\!\text{ + }\!\!\beta\!\!\text{ }=-\left( \dfrac{-1}{1} \right)=1$ 

The product of the zeros, $\text{ }\alpha\beta\!\!\text{ }=\dfrac{-4}{1}=-4$ 

The value of $\dfrac{\text{1}}{\text{ }\!\!\alpha\!\!\text{ }}\text{+}\dfrac{\text{1}}{\text{ }\!\!\beta\!\!\text{ }}\text{- }\alpha\beta\!\!\text{ =}\dfrac{\text{ }\!\!\alpha\!\!\text{ + }\!\!\beta\!\!\text{ }}{\text{ }\alpha\beta\!\!\text{ }}\text{- }\alpha\beta\!\!\text{ }$ is

$\Rightarrow \dfrac{\text{1}}{\text{ }\!\!\alpha\!\!\text{ }}\text{+}\dfrac{\text{1}}{\text{ }\!\!\beta\!\!\text{ }}\text{-  }\alpha\beta\!\!\text{ }=\dfrac{1}{-4}-(-4)$

$\Rightarrow -\dfrac{1}{4}+4=\dfrac{15}{4}$

Thus, $\dfrac{\text{1}}{\text{ }\!\!\alpha\!\!\text{ }}\text{+}\dfrac{\text{1}}{\text{ }\!\!\beta\!\!\text{ }}\text{-  }\alpha\beta\!\!\text{ }=\dfrac{15}{4}$.

3. If the square of the difference of the zeros of the quadratic polynomial $f\left( x \right)={{\text{x}}^{2}}+px+45$ is equal to $144$ , find the value of $p$.               

Ans: It is given that ${{\text{( }\!\!\alpha\!\!\text{ - }\!\!\beta\!\!\text{ )}}^{\text{2}}}=144$

From the given quadratic polynomial, $f(x)={{x}^{2}}+px+45$,

The sum of the roots, $\text{ }\!\!\alpha\!\!\text{ + }\!\!\beta\!\!\text{ }=-p$ and the product of the roots, $\text{ }\alpha\beta\!\!\text{ }=45$. 

Since, ${{\text{( }\!\!\alpha\!\!\text{ - }\!\!\beta\!\!\text{ )}}^{\text{2}}}=144$

\[\Rightarrow {{\text{ }\!\!\alpha\!\!\text{ }}^{\text{2}}}\text{+}{{\text{ }\!\!\beta\!\!\text{ }}^{\text{2}}}\text{-2 }\alpha\beta\!\!\text{ }=144\] 

\[\Rightarrow {{\text{( }\!\!\alpha\!\!\text{ + }\!\!\beta\!\!\text{ )}}^{\text{2}}}\text{- 4 }\alpha\beta\!\!\text{ }=144\]

Substituting, $\text{ }\!\!\alpha\!\!\text{ + }\!\!\beta\!\!\text{ }=-p$ and $\text{ }\alpha\beta\!\!\text{ }=45$, we get:

\[\Rightarrow {{(-p)}^{2}}-4\times 45=144\]

\[\Rightarrow {{p}^{2}}=144+180\]

\[\Rightarrow {{p}^{2}}=324\]

\[\therefore p=\pm 18\].

4. Divide $(6{{x}^{3}}-26x-21+{{x}^{2}})$ by $(-7+3x)$.  

Ans: Dividing $(6{{x}^{3}}-26x-21+{{x}^{2}})$ by $(-7+3x)$, we obtain:

\[\begin{matrix} & 3x-7\overset{2x^2+5x+3}{\overline{)\,\,\,{6x^3}+x^2-26x-21}}\\ & \underline{6x^3-14x^2}\\ & \hspace{3.5cm}15{{x}^{2}}-26x-21\\ & \hspace{2.6cm}\underline{15x^2-35x\;} \\ & \hspace{5.3cm}9x-21 \\ & \hspace{5.4cm}\underline{9x-21} \\ & \hspace{6.5cm}\underline{\quad 0\quad} \end{matrix}\]

Thus, the quotient is:

Quotient $=2{{x}^{2}}+5x+3$. 

5. Find the value of ‘$k$ ’ such that the quadratic polynomial ${{x}^{2}}-(k+6)x+2(2k+1)$ has sum of the zeros is half of their product.

Ans: It is given that, Sum of the zeros $=\dfrac{1}{2}\times $ Product of the zeros.

From the given quadratic polynomial, ${{x}^{2}}-(k+6)x+2(2k+1)$, the sum of the zeros is $(k+6)$ and product of the zeros is $2(2k+1)$.

Hence,

$\Rightarrow (k+6)=\dfrac{1}{2}[2(2k+1)]$

$\Rightarrow k+6=2k+1$

$\Rightarrow k=5$.

6. If $\text{ }\!\!\alpha\!\!\text{ }$ and $\text{ }\!\!\beta\!\!\text{ }$ are the zeros of the quadratic polynomial $f\left( x \right)={{x}^{2}}-p\left( x+1 \right)-c$ , show that $\left( \text{ }\!\!\alpha\!\!\text{ +1} \right)\left( \text{ }\!\!\beta\!\!\text{ +1} \right)=1-c$.             

Ans: It is given that $\text{ }\!\!\alpha\!\!\text{ }$ and $\text{ }\!\!\beta\!\!\text{ }$ are the roots of the quadratic polynomial $f(x)={{x}^{2}}-p(x+1)-c$.

$f(x)={{x}^{2}}-px-(p+c)$

$\therefore \text{ }\!\!\alpha\!\!\text{ + }\!\!\beta\!\!\text{  = p }$ 

And $\text{ }\alpha\beta\!\!\text{ }=-(p+c)$

Thus,

$\Rightarrow \text{( }\!\!\alpha\!\!\text{ +1)( }\!\!\beta\!\!\text{ +1)= }\alpha\beta\!\!\text{ +( }\!\!\alpha\!\!\text{ + }\!\!\beta\!\!\text{ )}+1$

$\Rightarrow \text{( }\!\!\alpha\!\!\text{ +1)( }\!\!\beta\!\!\text{ +1)}=-p-c+p+1$

$\Rightarrow \text{( }\!\!\alpha\!\!\text{ +1)( }\!\!\beta\!\!\text{ +1)}=1-c$.

7. If the sum of the zeros of the quadratic polynomial $f(t)=k{{t}^{2}}+2t+3k$ is equal to their product, find the value of ‘$k$

Ans: The given quadratic polynomial is, $f(t)=k{{t}^{2}}+2t+3k$.

It is given that, sum of the zeros = product of the zeros

Hence,

$\Rightarrow \dfrac{-2}{k}=\dfrac{3k}{k}$

$\Rightarrow k=-\dfrac{2}{3}$ .

8. Divide $({{x}^{4}}-5x+6)$ by $(2-{{x}^{2}})$. 

Ans: Dividing $({{x}^{4}}-5x+6)$ by $(2-{{x}^{2}})$, we obtain:

\[\begin{matrix} & \quad2-x^2\overset{-x^2-2}{\overline{){x^4}\qquad\quad-5x+6}}\\ & \;\;\;\;\underline{x^4-2x^2\quad}\\ & \hspace{2.8cm}2{{x}^{2}}-5x+6\\ & \hspace{2.8cm}\underline{2x^2\qquad-4} \\ & \hspace{3.5cm}\underline{\quad\quad-5x+10\quad} \end{matrix}\]

$\therefore $ Quotient $=-{{x}^{2}}-2$

Remainder $=-5x+10$

9. Find the zeros of the polynomial $p(x)=4\sqrt{3}{{x}^{2}}+5x-2\sqrt{3}$ and verify the relationship between the zeros and its coefficients.

Ans: The given polynomial is, $p(x)=4\sqrt{3}{{x}^{2}}+5x-2\sqrt{3}$.

It can be written as: $p(x)=4\sqrt{3}{{x}^{2}}+8x-3x-2\sqrt{3}$.

Hence,

$\Rightarrow p(x)=4x(\sqrt{3}x+2)-\sqrt{3}(\sqrt{3}x+2)$

$\Rightarrow p(x)=(4x-\sqrt{3})(\sqrt{3}x+2)$

Thus, the zeros are $4x-\sqrt{3}=0$ and $\sqrt{3}x+2=0$ 

$\Rightarrow x=\dfrac{\sqrt{3}}{4}$ and $x=-\dfrac{2}{\sqrt{3}}$

We know, sum of the zeros $=\dfrac{-\text{ Coefficient of }x}{\text{ Coefficient of }{{x}^{2}}}$

$=\left[ \dfrac{\sqrt{3}}{4}+\dfrac{(-2)}{\sqrt{3}} \right]=\dfrac{-5}{4\sqrt{3}}$ 

Similarly, the product of the zeros $=\dfrac{\text{Constant term}}{\text{ Coefficient of }{{x}^{2}}}$

$\Rightarrow \dfrac{-2\sqrt{3}}{4\sqrt{3}}=\dfrac{-1}{2}$ .

10. Find the value of ‘$k$’ so that the zeros of the quadratic polynomial $3{{x}^{2}}-kx+14$ are in the ratio $7:6$.

Ans: Let the zeros of the quadratic polynomial, $3{{x}^{2}}-kx+14$ be \[7p\] and \[6p\].

$\therefore 7p+6p=\dfrac{-(-k)}{3}=\dfrac{k}{3}$ 

$\Rightarrow 39p=k$

Also, $7p\times 6p=\dfrac{14}{3}$ 

$\Rightarrow 42{{p}^{2}}=\dfrac{14}{3}$

$\Rightarrow p=3$ 

Thus,

$\Rightarrow k=39\times 3$

$\Rightarrow k=117$.

11. If one zero of the quadratic polynomial $f(x)=4{{x}^{2}}-8kx-9$ is negative of the other, find the value of ‘$k$’.

Ans: It is given that one zero of the quadratic polynomial $f(x)=4{{x}^{2}}-8kx-9$ is the negative of the other,

Let us take one zero to be $\alpha $, then the other is $-\alpha $. 

Hence, the sum of the zeros $=0$

$\Rightarrow \dfrac{8k}{4}=0$

$\Rightarrow k=0$

12. Check whether the polynomial $({{t}^{2}}-3)$ is a factor of the polynomial $2{{t}^{4}}+3{{t}^{3}}-2{{t}^{2}}-9t-12$ by Division method.                                                

Ans: To determine whether the polynomial, $({{t}^{2}}-3)$ is a factor of the polynomial $2{{t}^{4}}+3{{t}^{3}}-2{{t}^{2}}-9t-12$ by division method, divide $2{{t}^{4}}+3{{t}^{3}}-2{{t}^{2}}-9t-12$ from $({{t}^{2}}-3)$. Thus, we have

\[\begin{matrix} & \;\;\;\;\qquad t^3-3\overset{2t^2+3t+4}{\overline{){2t^4+3t^3}-2t^2-9t-12}}\\ & \;\;\;\;\;\underline{2t^4\quad\quad\;\;\;-6t^2}\\ & \hspace{3.8cm}3{{t}^{3}}+4{{t}^{2}}-9t-12\\ & \hspace{2.9cm}\underline{3t^3\qquad\quad-9t} \\ & \hspace{5cm}4t^2\qquad-12 \\ & \hspace{5cm}\underline{4t^2\qquad-12} \\ & \hspace{6cm}\underline{\qquad\quad0\quad} \end{matrix}\]  

$\therefore ({{t}^{2}}-3)$ is the factor of given polynomial $2{{t}^{4}}+3{{t}^{3}}-2{{t}^{2}}-9t-12$.

Short Answer Questions (3 Marks)

1. Apply division algorithm to find the quotient $q\left( x \right)$ and remainder $r\left( x \right)$ an dividing $f\left( x \right)$ by $g\left( x \right)$ where $f(x)={{x}^{3}}-6{{x}^{2}}+11x-6$ , $g(x)={{x}^{2}}+x+1$. 

Ans: According to the division algorithm, $f(x)=g(x)\times q(x)+r(x)$.

Thus, dividing ${{x}^{3}}-6{{x}^{2}}+11x-6$ from ${{x}^{2}}+x+1$, we obtain:

\[\begin{matrix} & x^2+x+1\overset{x-7}{\overline{){x^3}-6x^2+11x-6}}\\ & \qquad\quad\underline{x^3+\;x^2+\;\;\;x}\\ & \hspace{2.8cm}-7{{x}^{2}}+10x-6\\ & \hspace{2.6cm}\underline{-7x^2-\;\;7x-7} \\ & \hspace{4.2cm}\underline{\quad17x+1\quad} \end{matrix}\]

Hence,

$({{x}^{3}}-6{{x}^{2}}+11x-6)={{x}^{2}}+2x+1(x-7)+(17x+1)$ .

2. If two zeros of the polynomial ${{x}^{4}}-6{{x}^{3}}-26{{x}^{2}}+138x-35$ are $2\pm \sqrt{3}$ , find the other zeros.

Ans: It is given that the two zeros of the polynomial ${{x}^{4}}-6{{x}^{3}}-26{{x}^{2}}+138x-35$ are $2+\sqrt{3}$ and $2-\sqrt{3}$.

Therefore, the sum of zeros is $2+\sqrt{3}+2-\sqrt{3}=4$

and product of the zeros is $1$. 

Hence,$({{x}^{2}}-4x+1)$ is the factor of ${{x}^{4}}-6{{x}^{3}}-26{{x}^{2}}+138x-35$.

So, the other factors can be determined by:

$\begin{matrix} & \quad x^2-4x+1\overset{x^2-2x-35}{\overline{){x^4-6x^3}-26x^2+138x-35}}\\ & \underline{x^4-4x^3+x^2}\\ & \hspace{3.6cm}-2{{x}^{3}}-27{{x}^{2}}+138x-35\\ & \hspace{2.6cm}\underline{-2x^3\;+\;8x^2\;- \;2x} \\ & \hspace{5cm}-35x^2+140x-35 \\ & \hspace{5cm}\underline{-35x^2+140x-35} \\ & \hspace{5cm}\underline{\qquad\quad0\quad\qquad} \end{matrix}$

Now,

$\Rightarrow {{x}^{2}}-2x-35={{x}^{2}}-7x+5x-35$ 

$\Rightarrow x(x-7)+5(x-7)$

$\Rightarrow {{x}^{2}}-2x-35=(x+5)(x-7)$

Thus, the zeros are

$x=7$ and $x=-5$

So, the other two zeros are $7$ and $-5$.

3. What must be subtracted from the polynomial $f(x)={{x}^{4}}+2{{x}^{3}}-13{{x}^{2}}-12x+21$ so that the resulting polynomial is exactly divisible by $g(x)={{x}^{2}}-2x+3$. 

Ans: According to the division algorithm, $f(x)=g(x)\times q(x)+r(x)$ .

Thus, $f(x)-r(x)=g(x)\times q(x)$

Dividing $f(x)={{x}^{4}}+2{{x}^{3}}-13{{x}^{2}}-12x+21$ from $g(x)={{x}^{2}}-2x+3$, we obtain:

\[\begin{matrix} & x^2-4x+3\overset{x^2+6x+8}{\overline{){x^4+2x^3}-13x^2-12x+21}} \\ & \ underline{x^4-4x^3+\;3x^2} \\ & \hspace{3.5cm}6{{x}^{3}}-16{{x}^{2}}-12x+21 \\ & \ hspace{2.5cm}\underline{6x^3-24x^2+18x} \\ & \hspace{4.9cm}8x^2-30x+21 \\ & \ hspace{5cm}\underline{8x^2-32x+24} \\ & \hspace{5.4cm}\underline{\qquad\quad2x-3\quad}\end{matrix}\]

Thus, we must be subtract $(2x-3)$ from $f(x)={{x}^{4}}+2{{x}^{3}}-13{{x}^{2}}-12x+21$ so that the resulting polynomial is exactly divisible by $g(x)={{x}^{2}}-2x+3$.

4. What must be added to $6{{x}^{5}}+5{{x}^{4}}+11{{x}^{3}}-3{{x}^{2}}+x+5$ so that it may be exactly divisible by $3{{x}^{2}}-2x+4$?

Ans: Dividing $6{{x}^{5}}+5{{x}^{4}}+11{{x}^{3}}-3{{x}^{2}}+x+5$ from \[3{{x}^{2}}-2x+4\], we obtain:

\[\begin{matrix} & \ quad3x^2-2x+4\overset{2x^3+3x^2+3x+3}{\overline{){6x^5+5x^4+11x^3}-3x^ +x+5}}\\ & \underline{6x^5-4x^4+8x^3}\\ & \hspace{4cm}9{{x}^{4}}+3x^3-3{{x}^{2}}+x+5\\ & \hspace{2.8cm}\underline{9x^4-6x^3+12x^2} \\ & \hspace{5.6cm}9x^3-15x^2+x+5 \\ & \hspace{5.3cm}\underline{9x^3-\;6x^2+12x} \\ & \hspace{6.8cm}-9x^2-11x+5 \\ & \hspace{7cm}\underline{-9x^2-6x+12} \\ & \hspace{7.1cm}\underline{\qquad\quad-17x-7\quad} \end{matrix}\]

So, we must add \[(3{{x}^{2}}-2x+4)-(-17x-7)\] , i.e.,

\[\Rightarrow 3{{x}^{2}}-2x+4+17x+7\]

\[\Rightarrow 3{{x}^{2}}+15x+13\].

Hence, we would add \[3{{x}^{2}}+15x+13\] to $6{{x}^{5}}+5{{x}^{4}}+11{{x}^{3}}-3{{x}^{2}}+x+5$ so that it is exactly divisible by \[3{{x}^{2}}-2x+4\].

5. Find all the zeros of the polynomial $f(x)=2{{x}^{4}}-3{{x}^{3}}-3{{x}^{2}}+6x-2$ , if being given that two of its zeros are $\sqrt{2}$ and $\text{-}\sqrt{2}$.

Ans: The two zeros of the polynomial \[f(x)=2{{x}^{4}}-3{{x}^{3}}-3{{x}^{2}}+6x-2\] are $\sqrt{2}$ and $-\sqrt{2}$.

\[\therefore (x-\sqrt{2})(x+\sqrt{2})\] or \[{{\left( x-2 \right)}^{2}}\] is the factor of the given polynomial.

\[\begin{matrix} & \quad x^2-2\overset{2x-3x+1}{\overline{){2x^4-3x^3}-3x^2+6x-2}}\\ & \underline{\;2x^4\qquad\quad-4x^2}\\ & \hspace{2.5cm}-3{{x}^{3}}\;+\;{{x}^{2}}+6x-2\\ & \hspace{1.7cm}\underline{-3x^3\qquad\quad+6x} \\ & \hspace{4.5cm}x^2\qquad-2 \\ & \hspace{4.5cm}\underline{x^2\qquad-2} \\ & \hspace{5cm}\underline{\qquad\quad0\quad} \end{matrix}\] 

The quotient is \[q(x)=2{{x}^{2}}-3x+1\]. Thus,

\[q(x)=2{{x}^{2}}-3x+1\] 

\[\Rightarrow 2{{x}^{2}}-2x-x+1\]

\[\Rightarrow 2x(x-1)-1(x-1)\]

\[q(x)=(2x-1)(x-1)\]

Hence, the other two zeroes are

\[x=1\] and \[x=\dfrac{1}{2}\].

6. On dividing ${{x}^{3}}-3{{x}^{2}}+x+2$ by a polynomial $g(x)$ the quotient and the remainder were $(x-2)$ and $-2x+4$ respectively, find $g(x)$

Ans: According to the division algorithm, $f(x)=g(x)\times q(x)+r(x)$.

$\therefore g(x)=\dfrac{p(x)-r(x)}{q(x)}$.

Substituting for $p\left( x \right)={{x}^{3}}-3{{x}^{2}}+x+2$, $q(x)=\left( x-2 \right)$ and $r(x)=-2x+4$, we get:

$g\left( x \right)=\dfrac{{{x}^{3}}-3{{x}^{2}}+x+2+2x-4}{x-2}$ 

Thus,

\[\begin{matrix} & \quad x-2\overset{x^2-x+1}{\overline{){x^3}-3x^2+3x-2}}\\ & \underline{x^3-2x^2}\\ & \hspace{2.6cm}-{{x}^{2}}+3x-2\\ & \hspace{1.8cm}\underline{-x^2+2x} \\ & \hspace{4cm}x-2 \\ & \hspace{4cm}\underline{x-2} \\ & \hspace{4cm}\underline{\qquad\quad0\quad} \end{matrix}\]

Hence, $g(x)={{x}^{2}}-x+1$.

7. Find all zeros of $f(x)=2{{x}^{3}}-7{{x}^{2}}+3x+6$ if its two zeros are $-\sqrt{\dfrac{3}{2}}$ and $\sqrt{\dfrac{3}{2}}$ . 

Ans: The two zeros of the given polynomial, $f(x)=2{{x}^{4}}-2{{x}^{3}}-7{{x}^{2}}+3x+6$ are  $-\sqrt{\dfrac{3}{2}}$ and $\sqrt{\dfrac{3}{2}}$ 

\[\therefore \left( x+\sqrt{\dfrac{3}{2}} \right)\left( x-\sqrt{\dfrac{3}{2}} \right)=\dfrac{1}{2}(2{{x}^{2}}-3)\] 

So, $(2{{x}^{2}}-3)$ is the factor of $f(x)$.

Dividing  $f(x)=2{{x}^{4}}-2{{x}^{3}}-7{{x}^{2}}+3x+6$ from $(2{{x}^{2}}-3)$, we get:

\[\begin{matrix} & 2x^2-3\overset{x^2-x-2}{\overline{){2x^4-2x^3}-7x^2+3x+6}}\\ & \underline{2x^4\qquad\quad-3x^2}\\ & \hspace{2.5cm}-2{{x}^{3}}\;-4{{x}^{2}}+3x+6\\ & \hspace{2.7cm}\underline{-2x^3\qquad\quad+3x\qquad} \\ & \hspace{3.8cm}-4x^2\quad\quad\;\;+6 \\ & \hspace{3.8cm}\underline{-4x^2\quad\quad\;\;+6} \\ & \hspace{4cm}\underline{\qquad\quad0\quad} \end{matrix}\]

Thus, we have

$g(x)={{x}^{2}}-x-2$ 

$\Rightarrow \text{ }{{x}^{2}}-2x+x-2$

$\Rightarrow x(x-2)+1(x-2)$

$g\left( x \right)=(x+1)(x-2)$

Hence, the other two zeros are

$x=-1$ and 

$x=2$ 

8. Obtain all zeros of the polynomial $f(x)=2{{x}^{4}}+{{x}^{3}}-14{{x}^{2}}-19x-6$ , if two of its zeros are $-2$ and $-1$.  

Ans: The two zeros of the given polynomial, $f(x)=2{{x}^{4}}+{{x}^{3}}-14{{x}^{2}}-19x-6$ are  $-2$ and $-1$. 

$\therefore (x+2)(x+1)={{x}^{2}}+3x+2$ 

So, ${{x}^{2}}+3x+2$ is the factor of $f\left( x \right)$.

Dividing $f(x)=2{{x}^{4}}+{{x}^{3}}-14{{x}^{2}}-19x-6$ from ${{x}^{2}}+3x+2$, we get:

\[\begin{matrix} & x^2-3x+2\overset{2x^2-5x-3}{\overline{){2x^4+x^3}-14x^2-19x-6}}\\ & \quad\underline{2x^4+6x^3+4x^2}\\ & \hspace{3.4cm}-5{{x}^{3}}-18{{x}^{2}}-19x-6\\ & \hspace{2.6cm}\underline{-5x^3-15x^2-10x} \\ & \hspace{4.7cm}-\;3x^2\;-\;9x\;-\;6 \\ & \hspace{4.8cm}\underline{-\;3x^2\;-\;9x\;-\;6} \\ & \hspace{5cm}\underline{\qquad\quad0\quad} \end{matrix}\] 

Thus, we have

$g(x)=2{{x}^{2}}-5x-3$ 

$\Rightarrow \text{ 2}{{x}^{2}}-6x+x-3$

$\Rightarrow 2x(x-3)+1(x-3)$

$g\left( x \right)=(x-3)(2x+1)$

Hence, the other two zeros are

$x=3$ and 

$x=-\dfrac{1}{2}$ 

Other two zeros are $3$ and $-\dfrac{1}{2}$ .

9. Obtain all other zeros of $3{{x}^{4}}+6{{x}^{3}}-2{{x}^{2}}-10x-5$ if its two zeros are $-\sqrt{\dfrac{5}{3}}$ and $\sqrt{\dfrac{5}{3}}$.

Ans: The two zeros of the given polynomial, $3{{x}^{4}}+6{{x}^{3}}-2{{x}^{2}}-10x-5$ are  $-\sqrt{\dfrac{5}{3}}$ and $\sqrt{\dfrac{5}{3}}$. 

$\therefore \left( x+\sqrt{\dfrac{5}{3}} \right)\left( x-\sqrt{\dfrac{5}{3}} \right)=\dfrac{1}{3}(3{{x}^{2}}-5)$ 

So, $(3{{x}^{2}}-5)$ is the factor of $f\left( x \right)$.

Dividing $3{{x}^{4}}+6{{x}^{3}}-2{{x}^{2}}-10x-5$ from $(3{{x}^{2}}-5)$, we get:

\[\begin{matrix} & \quad3x^2-5\overset{x^2+2x+1}{\overline{){3x^4+6x^3}-2x^2-10x-5}}\\ & \underline{3x^4\qquad\;\;\;-5x^2}\\ & \hspace{3.2cm}6{{x}^{3}}+3{{x}^{2}}-10x-5\\ & \hspace{2.5cm}\underline{6x^3\qquad\quad-10x} \\ & \hspace{4.5cm}3x^2\qquad\quad-5 \\ & \hspace{4.5cm}\underline{3x^2\qquad\quad-5} \\ & \hspace{5cm}\underline{\qquad\quad0\quad} \end{matrix}\]

Thus, we have

$g(x)={{x}^{2}}+2x+1$ 

$g\left( x \right)={{(x+1)}^{2}}$

Hence, the other two zeros are

$x=-1$ and 

$x=-1$ 

Other two zeros are $-1$ and $-1$.

10. If the polynomial ${{x}^{4}}-6{{x}^{3}}+16{{x}^{2}}-25x+10$ is divided by another polynomial ${{x}^{2}}-2x+k$ , the remainder comes out to be $(x+a)$ , find ‘$k$ ’ and ‘$a$ ’.

Ans: Dividing ${{x}^{4}}-6{{x}^{3}}+16{{x}^{2}}-25x+10$ from ${{x}^{2}}-2x+k$, we get: 

\[\begin{matrix} & x^2-2x+k\overset{x^2-4x+(8-k)}{\overline{){x^4-6x^3}+16x^2-25x+10}}\\ & \underline{x^4-2x^3+kx^2}\\ & \hspace{4cm}-4{{x}^{3}}+(16-k){{x}^{2}}-25x+10\\ & \hspace{2.6cm}\underline{-4x^3\;+\;8x^2\;- \;4kx} \\ & \hspace{5.6cm}(8-k)x^2+(4k-25)x+10 \\ & \hspace{7cm}\underline{(8-k)x^2-(16-2k)x+(8k-k^2)} \\ & \hspace{7cm}\underline{\qquad\quad(2k-9)x+(k^2-8k+10)\quad} \end{matrix}\]

But remainder is given to be $(x+a)$ 

Thus, equating the coefficient of $x$ and constant term

So $2k-8k+10=a$ 

$\Rightarrow 25-40+10=a$ 

$\Rightarrow -5=a$

Hence, $k=5$ and $\text{a}=-5$. 

11. Find the value of ‘$k$ ’ for which the polynomial ${{x}^{4}}+10{{x}^{3}}+25{{x}^{2}}+15x+k$ is exactly divisible by $(x+7)

Ans: Since $p(x)={{x}^{4}}+10{{x}^{3}}+25{{x}^{2}}+15x+k$ is exactly divisible by $(x+7)$ therefore, $(x+7)$ is the factor.

Hence, $p(-7)=0$ 

$\Rightarrow {{(-7)}^{4}}+10{{(-7)}^{3}}+25{{(-7)}^{2}}+15(-7)+k=0$

$\Rightarrow 2401-3430+1225-105+k=0$

$\Rightarrow k=91$. 

12. If $\alpha $ and $\beta $ are the zeros of the polynomial\[f(x)={{x}^{2}}+px+q\] , find polynomial whose zeros are \[{{\left( \alpha +\beta  \right)}^{2}}\] and \[{{\left( \alpha -\beta  \right)}^{2}}\] .

Ans: If the zeros of the polynomial $f(x)={{x}^{2}}+px+q$ are taken as $\alpha $ and $\beta $.

Then,

$\alpha +\beta =-p$ and $\alpha \beta =q$ 

We know \[{{(\alpha -\beta )}^{2}}={{(\alpha +\beta )}^{2}}-4\alpha \beta \] 

\[\Rightarrow {{(\alpha -\beta )}^{2}}={{(-p)}^{2}}-4q\] 

\[\Rightarrow {{(\alpha -\beta )}^{2}}=-{{p}^{2}}-4q\]

If zeros are ${{(\alpha +\beta )}^{2}}$ and ${{(\alpha -\beta )}^{2}}$

Then, sum of zeros

${{(\alpha +\beta )}^{2}}+{{(\alpha -\beta )}^{2}}={{(-p)}^{2}}+({{p}^{2}}-4q)$ 

${{(\alpha +\beta )}^{2}}+{{(\alpha -\beta )}^{2}}=4{{p}^{2}}-4{{p}^{2}}q$

And the product of the zeros  ${{(\alpha +\beta )}^{2}}\times {{(\alpha -\beta )}^{2}}={{p}^{4}}-4{{p}^{2}}q$

Hence, the required polynomial is

${{x}^{2}}-(\text{sum of zeros)}x+\text{product of zeros}$ 

$\Rightarrow {{x}^{2}}-(2{{p}^{2}}-4q)x+4{{p}^{2}}-4{{p}^{2}}q$ 

$\Rightarrow {{x}^{2}}-2{{p}^{2}}x-4qx+{{p}^{4}}-4{{p}^{2}}q$

Long Answer Questions                                            (4 Marks)

1. Divide the polynomial $p(x)$ by the polynomial $g(x)$ and find the quotient and remainder in each of the following.

i. $p(x)={{x}^{3}}-3{{x}^{2}}+5x-3$, $g(x)={{x}^{2}}-2$ 

Ans: Dividing the polynomial \[p(x)={{x}^{3}}-3{{x}^{2}}+5x-3\] by the polynomial \[g(x)={{x}^{2}}-2\], we obtain: 

\[\begin{matrix} & x^2-2\overset{x-3}{\overline{){x^3}-3x^2+5x-3}}\\ & \quad\underline{x^3\qquad\quad-2x}\\ & \hspace{2cm}-3{{x}^{2}}+7x-3\\ & \hspace{1cm}\underline{-3x^2+6} \\ & \hspace{2.8cm}\underline{\qquad\quad 7x-9\quad} \end{matrix}\] 

\[\therefore \] quotient \[=x-3\] and remainder $=7x-9$ 

ii. $p(x)={{x}^{4}}-3{{x}^{2}}+4x+5$, $g(x)={{x}^{2}}-x+1$ 

Ans: Dividing the polynomial \[p(x)={{x}^{4}}-3{{x}^{2}}+4x+5\] by the polynomial \[g(x)={{x}^{2}}-x+1\], we obtain: 

\[\begin{matrix} & x^2-x+1\overset{x^2+x-3}{\overline{){x^4}-3x^2+4x+5}}\\ & \qquad\quad\underline{x^4+x^2-x^3}\\ & \hspace{3.6cm}-4{{x}^{2}}+4x+5+{{x}^{3}}\\ & \hspace{3.8cm}\underline{-x^2\;+\;x\;\;\; \quad +x^3} \\ & \hspace{2.7cm}-3x^2+3x+5 \\ & \hspace{2.7cm}\underline{-3x^2+3x-3} \\ & \hspace{4.5cm}\underline{\qquad\quad8\quad} \end{matrix}\] 

\[\therefore \] quotient $={{x}^{2}}+x-3$ and remainder \[=8\]. 

iii. $p(x)={{x}^{4}}-5x+6$, $g(x)=2-{{x}^{2}}$ 

Ans: Dividing the polynomial \[p(x)={{x}^{4}}-5x+6\] by the polynomial \[g(x)=2-{{x}^{2}}\], we obtain: 

\[\begin{matrix} & -x^2+2\overset{-x^2-2}{\overline{){x^4}\qquad-5x+6}}\\ & \quad\underline{x^4-2x^2}\\ & \hspace{4.5cm}-5x+6+2x^2\\ & \hspace{4.6cm}\underline{\qquad-4+2x^2} \\ & \hspace{3.5cm}\underline{\quad-5x+10\quad} \end{matrix}\] 

\[\therefore \] quotient \[=-{{x}^{2}}-2\] and remainder \[=-5x+10\].

2. Check whether the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial.

1.  ${{t}^{2}}-3$, $2{{t}^{4}}+3{{t}^{3}}-2{{t}^{2}}-9t-12$ 

Ans: Dividing the second polynomial \[2{{t}^{4}}+3{{t}^{3}}-2{{t}^{2}}-9t-12\] by the first polynomial \[{{t}^{2}}-3\] , we obtain: 

\[\begin{matrix} & \quad t^2-3\overset{2t^2+3t+4}{\overline{){2t^4+3t^3}-2t^2-9t-12}}\\ & \underline{2t^4\qquad\quad-6t^2}\\ & \hspace{3cm}3{{t}^{3}}+4{{t}^{2}}-9t-12\\ & \hspace{2cm}\underline{3t^3\qquad\quad-9t} \\ & \hspace{4cm}4t^2\quad\quad-12 \\ & \hspace{4cm}\underline{4t^2\quad\quad-12} \\ & \hspace{5cm}\underline{\qquad\quad0\quad} \end{matrix}\]

The remainder obtained is $0$. 

Hence, the first polynomial, \[{{t}^{2}}-3\] is a factor of second polynomial, \[2{{t}^{4}}+3{{t}^{3}}-2{{t}^{2}}-9t-12\].

ii. ${{x}^{2}}+3x+1$, $3{{x}^{4}}+5{{x}^{3}}-7{{x}^{2}}+2x+2$ 

Ans: Dividing the second polynomial \[3{{x}^{4}}+5{{x}^{3}}-7{{x}^{2}}+2x+2\] by the first polynomial \[{{x}^{2}}+3x+1\] , we obtain: 

\[\begin{matrix} & x^2+3x+1\overset{3x^2-4x+2}{\overline{){3x^4+5x^3}-7x^2+2x+2}}\\ & \qquad\underline{3x^4+9x^3+3x^2}\\ & \hspace{3.6cm}-4{{x}^{3}}-10{{x}^{2}}+2x+2\\ & \hspace{2.8cm}\underline{-4x^3-12x^2-4x} \\ & \hspace{5.5cm}2x^2+6x+2 \\ & \hspace{5.5cm}\underline{2x^2+6x+2} \\ & \hspace{6cm}\underline{\qquad\quad0\quad} \end{matrix}\]

The remainder obtained is $0$. 

Hence, the first polynomial, \[{{x}^{2}}+3x+1\] is a factor of second polynomial, \[3{{x}^{4}}+5{{x}^{3}}-7{{x}^{2}}+2x+2\].

iii. ${{x}^{3}}-3x+1$, ${{x}^{5}}-4{{x}^{3}}+{{x}^{2}}+3x+1$ 

Ans: Dividing the second polynomial \[{{x}^{5}}-4{{x}^{3}}+{{x}^{2}}+3x+1\] by the first polynomial \[{{x}^{3}}-3x+1\] , we obtain: 

\[\begin{matrix} & x^3-3x+1\overset{x^2-1}{\overline{){x^5-4x^3}+x^2+3x+1}}\\ & \quad\;\underline{x^5-3x^3+x^2}\\ & \hspace{3.1cm}-{{x}^{3}}\qquad\quad+3x+1\\ & \hspace{3.1cm}\underline{-{{x}^{3}}\qquad\quad+3x+1} \\ & \hspace{5cm}\underline{\qquad 2\quad} \end{matrix}\]

The remainder obtained is $2$.  Thus, the remainder is not equal to $0$.

Hence, the first polynomial, \[{{x}^{3}}-3x+1\] is a factor of second polynomial, \[{{x}^{5}}-4{{x}^{3}}+{{x}^{2}}+3x+1\].

3. Obtain all other zeros of $\left( 3{{x}^{4}}+6{{x}^{3}}-2{{x}^{2}}-10x-5 \right)$, if its two zeros are $-\sqrt{\dfrac{5}{3}}$ and $\sqrt{\dfrac{5}{3}}$.

Ans: The two zeros of the given polynomial, $3{{x}^{4}}+6{{x}^{3}}-2{{x}^{2}}-10x-5$ are  $-\sqrt{\dfrac{5}{3}}$ and $\sqrt{\dfrac{5}{3}}$. 

$\therefore \left( x+\sqrt{\dfrac{5}{3}} \right)\left( x-\sqrt{\dfrac{5}{3}} \right)=\dfrac{1}{3}(3{{x}^{2}}-5)$ 

So, $(3{{x}^{2}}-5)$ is the factor of $f\left( x \right)$.

Dividing $3{{x}^{4}}+6{{x}^{3}}-2{{x}^{2}}-10x-5$ from $(3{{x}^{2}}-5)$, we get:

\[\begin{matrix} & \quad 3x^2-5\overset{x^2+2x+1}{\overline{){3x^4+6x^3}-2x^2-10x-5}}\\ & \underline{3x^4\qquad\quad-5x^2}\\ & \hspace{3.3cm}6{{x}^{3}}+3{{x}^{2}}-10x-5\\ & \hspace{2.5cm}\underline{6x^3\qquad\quad-10x} \\ & \hspace{3.4cm}3x^2-5 \\ & \hspace{3.4cm}\underline{3x^2-5} \\ & \hspace{3.5cm}\underline{\qquad\quad0\quad} \end{matrix}\]

Thus, we have

$g(x)={{x}^{2}}+2x+1$ 

$g\left( x \right)={{(x+1)}^{2}}$

Hence, the other two zeros are

$x=-1$ and 

$x=-1$ 

Other two zeros are $-1$ and $-1$.

4. On dividing $({{x}^{3}}-3{{x}^{2}}+x+2)$ by a polynomial $g(x)$ the quotient and the remainder were $(x-2)$ and $(-2x+4)$ respectively, find $g(x)$.

Ans: According to the division algorithm, $p(x)=g(x)\times q(x)+r(x)$.

$\therefore g(x)=\dfrac{p(x)-r(x)}{q(x)}$.

Substituting for $p\left( x \right)={{x}^{3}}-3{{x}^{2}}+x+2$, $q(x)=\left( x-2 \right)$ and $r(x)=-2x+4$, we get:

$g\left( x \right)=\dfrac{{{x}^{3}}-3{{x}^{2}}+x+2+2x-4}{x-2}$ 

Thus,

\[\begin{matrix} & \quad \;\;x-2\overset{x^2-x+1}{\overline{)x^3-3x^2+3x-2}}\\ & \underline{x^3-2x^2}\\ & \hspace{2.3cm}-\;\;{{x}^{2}}+3x-2\\ & \hspace{2cm}\underline{-\;\;x^2+2x\quad} \\ & \hspace{4cm}x-2 \\ & \hspace{4cm}\underline{x-2} \\ & \hspace{4cm}\underline{\quad\quad0\quad} \end{matrix}\]

Hence, $g(x)={{x}^{2}}-x+1$.

5. Give examples of polynomials $p(x)$,$g(x)$, $q(x)$ and $r(x)$ , which satisfy the division algorithm and

i. $\text{deg }p(x)=\text{deg }q(x)$ 

Ans: According to the division algorithm, $p(x)=g(x)\times q(x)+r(x)$. 

Let $p(x)=3{{x}^{2}}+3x+6$ and $g(x)=3$. Performing long division, we have: 

\[\begin{matrix} & \quad3\overset{x^2+x+2}{\overline{)3x^2+3x+6}}\\ & \underline{3x^2\quad\quad}\\ & \hspace{2cm}3x+6\\ & \hspace{2cm}\underline{3x\qquad} \\ & \hspace{3cm}6 \\ & \hspace{3cm}\underline{6} \\ & \hspace{3cm}\underline{\quad0\quad} \end{matrix}\]

We can observe from the above example that $p(x)=g(x)\times q(x)+r(x)$, i.e., 

$3{{x}^{2}}+3x+6=\left( {{x}^{2}}+x+2 \right)\times 3+0$

Also, $\deg p(x)=\deg q(x)=2$.

ii. $\text{deg }q(x)=\text{deg }r(x)$ 

Ans: According to the division algorithm, $p(x)=g(x)\times q(x)+r(x)$. 

Let $p(x)={{x}^{3}}+5$ and $g(x)={{x}^{2}}-1$. Performing long division, we have:  

\[\begin{matrix} & x^2-1\overset{x}{\overline{)x^3\quad+5}}\\ & \qquad\quad\underline{x^3-x\quad}\\ & \hspace{2.5cm}\underline{\quad x+5 \quad} \end{matrix}\]

We can observe from the above example that $p(x)=g(x)\times q(x)+r(x)$, i.e., 

${{x}^{3}}+5=\left( {{x}^{2}}-1 \right)\times x+x+5$

Also, $\deg q(x)=\deg r(x)=1$.

iii. $\text{deg }r(x)=0$

Ans: According to the division algorithm, $p(x)=g(x)\times q(x)+r(x)$. 

Let $p(x)={{x}^{2}}+5x-3$ and $g(x)=x+3$. Performing long division, we have:  

\[\begin{matrix} & x+3\overset{x+2}{\overline{)x^2+5x-3}}\\ & \quad\underline{x^2+3x}\\ & \hspace{2.2cm}2x-3\\ &\hspace{2.2cm}\underline{2x+6} \\ &\hspace{2cm}\underline{\qquad\quad-9\quad} \end{matrix}\]

We can observe from the above example that $p(x)=g(x)\times q(x)+r(x)$, i.e., 

$3{{x}^{2}}+3x+6=\left( {{x}^{2}}+x+2 \right)\times 3+0$

Also, $\deg r(x)=0$.

6. Find the zeroes of the following quadratic polynomials and verify the relationship between the zeros and the coefficients.

i. ${{x}^{2}}-2x-8$ 

Ans: The given polynomial is ${{x}^{2}}-2x-8$.

Comparing given polynomial with general form $a{{x}^{2}}+bx+c$,

We get $a=1$, $b=-2$ and $c=-8$.

We have, ${{x}^{2}}-2x-8$

$\Rightarrow {{x}^{2}}-4x+2x-8$

$\Rightarrow x(x-4)+2(x-4)$

\[\Rightarrow (x-4)(x+2)\]

Equating this to $0$, we will find values of $2$ zeroes of this polynomial.

\[\Rightarrow (x-4)(x+2)=0\]

\[\Rightarrow x=4,-2\]are the two zeros.

Sum of zeroes \[=4-2=2=\dfrac{-(-2)}{1}=\dfrac{-b}{a}=\dfrac{-\text{ Coefficient of }x}{\text{ Coefficient of }{{x}^{2}}}\]

Product of zeroes \[=4\times -2=-8=\dfrac{-8}{1}=\dfrac{c}{a}=\dfrac{\text{ Constant term }}{\text{ Coefficient of }{{x}^{2}}}\]

ii. $4{{s}^{2}}-4s+1$

Ans:  The given polynomial is $4{{s}^{2}}-4s+1$.

Comparing given polynomial with general form $a{{x}^{2}}+bx+c$,

We get $a=4$, $b=-4$ and $c=1$.

We have, $4{{s}^{2}}-4s+1$

$\Rightarrow 4{{s}^{2}}-2s-2s+1$

$\Rightarrow 2s(2s-1)-1(2s-1)$

$\Rightarrow (2s-1)(2s-1)$

Equating this to $0$, we will find values of $2$ zeroes of this polynomial.

\[\Rightarrow (2s-1)(2s-1)=0\]

\[\Rightarrow s=\dfrac{1}{2},\dfrac{1}{2}\]are the two zeros.

Thus, the two zeroes of this polynomial are \[\dfrac{1}{2}\] and \[\dfrac{1}{2}\].

Sum of zeroes \[=\dfrac{1}{2}+\dfrac{1}{2}=1=\dfrac{-(-1)}{1}\times \dfrac{4}{4}=\dfrac{-(-4)}{4}=\dfrac{-b}{a}=\dfrac{-\text{ Coefficient of }x}{\text{ Coefficient of }{{x}^{2}}}\]

Product of zeroes \[=\dfrac{1}{2}\times \dfrac{1}{2}=\dfrac{1}{4}=\dfrac{c}{a}=\dfrac{\text{ Constant term }}{\text{ Coefficient of }{{x}^{2}}}\]

iii. $6{{x}^{2}}-3-7x$

Ans: The given polynomial is $6{{x}^{2}}-3-7x$.

Comparing given polynomial with general form $a{{x}^{2}}+bx+c$,

We get $a=6$, $b=-7$ and $c=-3$.

We have, $6{{x}^{2}}-3-7x$

$\Rightarrow 6{{x}^{2}}-9x+2x-3$

$\Rightarrow 3x(2x-3)+1(2x-3)$

$\Rightarrow (2x-3)(3x+1)$

Equating this to $0$, we will find values of $2$ zeroes of this polynomial.

$\Rightarrow (2x-3)(3x+1)=0$

$\Rightarrow x=\dfrac{3}{2},\dfrac{-1}{3}$

Thus, the two zeroes of this polynomial are $\dfrac{3}{2}$ and $\dfrac{-1}{3}$.

Sum of zeroes $=\dfrac{3}{2}+\dfrac{-1}{3}=\dfrac{9-2}{6}=\dfrac{7}{6}=\dfrac{-(-7)}{6}=\dfrac{-b}{a}=\dfrac{-\text{ Coefficient of }x}{\text{ Coefficient of }{{x}^{2}}}$

Product of zeroes $=\dfrac{3}{2}\times \dfrac{-1}{3}=\dfrac{-1}{2}=\dfrac{c}{a}=\dfrac{\text{ Constant term }}{\text{ Coefficient of }{{x}^{2}}}$

iv. $4{{u}^{2}}+8u$

Ans:  The given polynomial is $4{{u}^{2}}+8u$.

Comparing given polynomial with general form $a{{x}^{2}}+bx+c$,

We get $a=4$, $b=8$ and $c=0$.

We have, $4{{u}^{2}}+8u$

$\Rightarrow 4{{u}^{2}}+8u=4u(u+2)$

Equating this to $0$, we will find values of $2$ zeroes of this polynomial.

$\Rightarrow 4u(u+2)=0$

$\Rightarrow u=0,-2$

Thus, the two zeroes of this polynomial are $0$ and $-2$. 

Sum of zeroes $=0-2=-2=\dfrac{-(-2)}{1}\times \dfrac{4}{4}=\dfrac{-8}{4}=\dfrac{-b}{a}=\dfrac{-\text{ Coefficient of }x}{\text{ Coefficient of }{{x}^{2}}}$.

Product of zeroes $=0\times -2=0=\dfrac{0}{4}=\dfrac{c}{a}=\dfrac{\text{ Constant term }}{\text{ Coefficient of }{{x}^{2}}}$.

v. ${{t}^{2}}-15$

Ans: The given polynomial is ${{t}^{2}}-15$.

Comparing given polynomial with general form $a{{x}^{2}}+bx+c$,

We get $a=1$, $b=0$ and $c=-15$.

We have, ${{t}^{2}}-15$

$\Rightarrow {{t}^{2}}=15$

$\Rightarrow t=\pm \sqrt{15}$

Thus, the two zeroes of this polynomial are $\sqrt{15}$ and $-\sqrt{15}$. 

Sum of zeroes $=\sqrt{15}+(-\sqrt{15})=0=\dfrac{0}{1}=\dfrac{-b}{a}=\dfrac{-\text{ Coefficient of }x}{\text{ Coefficient of }{{x}^{2}}}$

Product of zeroes $=\sqrt{15}\times (-\sqrt{15})=-15=\dfrac{-15}{1}=\dfrac{c}{a}=\dfrac{\text{ Constant term }}{\text{ Coefficient of }{{x}^{2}}}$

vi. $3{{x}^{2}}-x-4$

Ans:  The given polynomial is $3{{x}^{2}}-x-4$.

Comparing given polynomial with general form $a{{x}^{2}}+bx+c$,

We get $a=3$, $b=-1$ and $c=-4$.

We have, $3{{x}^{2}}-x-4=3{{x}^{2}}-4x+3x-4$ 

$\Rightarrow x(3x-4)+1(3x-4)$

$\Rightarrow (3x-4)(x+1)$

Equating this to $0$, we will find values of $2$ zeroes of this polynomial.

$\Rightarrow (3x-4)(x+1)=0$

$\Rightarrow x=\dfrac{4}{3},-1$

Thus, the two zeroes of this polynomial are $\dfrac{4}{3}$ and $-1$. 

Sum of zeroes $=\dfrac{4}{3}+(-1)=\dfrac{4-3}{3}=\dfrac{1}{3}=\dfrac{-(-1)}{3}=\dfrac{-b}{a}=\dfrac{-\text{ Coefficient of }x}{\text{ Coefficient of }{{x}^{2}}}$

Product of zeroes $=\dfrac{4}{3}\times (-1)=\dfrac{-4}{3}=\dfrac{c}{a}=\dfrac{\text{ Constant term }}{\text{ Coefficient of }{{x}^{2}}}$.

7. Find a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively.

i. $\dfrac{1}{4},-1$ 

Ans: The sum of the zeros is given as $\dfrac{1}{4}$ and the product of the zeros is given to be $-1$.

Let quadratic polynomial be of the form $a{{x}^{2}}+bx+c$ and

Let $\alpha $ and $\beta $ are two zeroes of above quadratic polynomial.

$\alpha +\beta =\dfrac{1}{4}=\dfrac{-b}{a}$

$\alpha \times \beta =-1=\dfrac{-1}{1}\times \dfrac{4}{4}=\dfrac{-4}{4}=\dfrac{c}{a}$

$\therefore a=4,b=-1$ and $c=-4$ .

So, the equation becomes $4{{x}^{2}}-x-4$.

Thus, the quadratic polynomial which satisfies above conditions is $4{{x}^{2}}-x-4$ .

ii. $\sqrt{2},\dfrac{1}{3}$

Ans: The sum of the zeros is given as $\sqrt{2}$ and the product of the zeros is given to be $\dfrac{1}{3}$.

Let quadratic polynomial be of the form $a{{x}^{2}}+bx+c$ and

Let $\alpha $ and $\beta $ are two zeroes of above quadratic polynomial.

$\alpha +\beta =\sqrt{2}\times \dfrac{3}{3}=\dfrac{3\sqrt{2}}{3}=\dfrac{-b}{a}$

$\alpha \times \beta =\dfrac{1}{3}$ which is equal to $\dfrac{c}{a}$

$\therefore a=3,b=-3\sqrt{2}$ and $c=1$ .

So, the equation becomes $3{{x}^{2}}-3\sqrt{2}x+1$.

Thus, the quadratic polynomial which satisfies above conditions is $3{{x}^{2}}-3\sqrt{2}x+1$.

iii. $0,\sqrt{5}$

Ans: The sum of the zeros is given as $0$ and the product of the zeros is given to be $\sqrt{5}$.

Let quadratic polynomial be of the form $a{{x}^{2}}+bx+c$ and

Let $\alpha $ and $\beta $ are two zeroes of above quadratic polynomial.

$\alpha +\beta =0=\dfrac{0}{1}=\dfrac{-b}{a}$

$\alpha \times \beta =\sqrt{5}=\dfrac{\sqrt{5}}{1}=\dfrac{c}{a}$

$\therefore a=1,b=0$ and $c=\sqrt{5}$ .

So, the equation becomes ${{x}^{2}}+\sqrt{5}$.

Thus, the quadratic polynomial which satisfies above conditions is ${{x}^{2}}+\sqrt{5}$.

iv. $1,1$

Ans:  The sum of the zeros is given as $1$ and the product of the zeros is given to be $1$.

Let quadratic polynomial be of the form $a{{x}^{2}}+bx+c$ and

Let $\alpha $ and $\beta $ are two zeroes of above quadratic polynomial.

$\alpha +\beta =1=\dfrac{-(-1)}{1}=\dfrac{-b}{a}$

$\alpha \times \beta =1=\dfrac{1}{1}=\dfrac{c}{a}$

$\therefore a=1,b=-1$ and $c=1$ .

So, the equation becomes ${{x}^{2}}-x+1$.

Thus, the quadratic polynomial which satisfies above conditions is ${{x}^{2}}-x+1$ .

v. $\dfrac{-1}{4},\dfrac{1}{4}$

Ans: The sum of the zeros is given as $-\dfrac{1}{4}$ and the product of the zeros is given to be $\dfrac{1}{4}$.

Let quadratic polynomial be of the form $a{{x}^{2}}+bx+c$ and

Let $\alpha $ and $\beta $ are two zeroes of above quadratic polynomial.

$\alpha +\beta =\dfrac{-1}{4}=\dfrac{-b}{a}$

$\alpha \times \beta =\dfrac{1}{4}=\dfrac{c}{a}$

$\therefore a=4,b=1,c=1$

So, the equation becomes $4{{x}^{2}}+x+1$.

Thus, the quadratic polynomial which satisfies above conditions is $4{{x}^{2}}+x+1$ .

vi. $4,1$

Ans: The sum of the zeros is given as $4$ and the product of the zeros is given to be $1$.

Let quadratic polynomial be of the form $a{{x}^{2}}+bx+c$ and

Let $\alpha $ and $\beta $ are two zeroes of above quadratic polynomial.

$\alpha +\beta =4=\dfrac{-(-4)}{1}=\dfrac{-b}{a}$

$\alpha \times \beta =1=\dfrac{1}{1}=\dfrac{c}{a}$

$\therefore a=1,b=-4,c=1$

So, the equation becomes ${{x}^{2}}-4x+1$.

Thus, the quadratic polynomial which satisfies above conditions is ${{x}^{2}}-4x+1$.

8. Verify that the numbers given alongside of the cubic polynomials below are their zeroes. Also verify the relationship between the zeroes and the coefficients in each case:

i. $2{{x}^{3}}+{{x}^{2}}-5x+2$;$\dfrac{1}{2},1,-2$

Ans: The given polynomial is $2{{x}^{3}}+{{x}^{2}}-5x+2$.

Also, the given roots are $\dfrac{1}{2},1,-2$.

Comparing the given polynomial with $p\left( x \right)=a{{x}^{3}}+b{{x}^{2}}+cx+d$, we get

$a=2,b=1,c=-5$ and $d=2$.

Verifying whether $\dfrac{1}{2},1,-2$ are the roots of the cubic polynomial, we have:

$p\left( \dfrac{1}{2} \right)=2{{\left( \dfrac{1}{2} \right)}^{3}}+{{\left( \dfrac{1}{2} \right)}^{2}}-5\left( \dfrac{1}{2} \right)+2$

$\Rightarrow \dfrac{1}{4}+\dfrac{1}{4}-\dfrac{5}{2}+2$

$\Rightarrow \dfrac{1+1-10+8}{0}=0$

$p(1)=2{{(1)}^{3}}+{{(1)}^{2}}-5(1)+2$

$\Rightarrow 2+1-5+2=0$

$p(-2)=2{{(-2)}^{3}}+{{(-2)}^{2}}-5(-2)+2$

$\Rightarrow 2(-8)+4+10+2$

$\Rightarrow -16+16=0$

$\therefore \dfrac{1}{2},1$ and $-2$ are the zeroes of $2{{x}^{3}}+{{x}^{2}}-5x+2$.

Now, $\alpha +\beta +\gamma =\dfrac{1}{2}+1+(-2)=\dfrac{1+2-4}{2}=\dfrac{-1}{2}=\dfrac{-b}{a}$

And $\alpha \beta +\beta \gamma +\gamma \alpha =\left( \dfrac{1}{2} \right)(1)+(1)(-2)+(-2)\left( \dfrac{1}{2} \right)$

$\Rightarrow \dfrac{1}{2}-2-1=\dfrac{-5}{2}=\dfrac{c}{a}$.

And $\alpha \beta \gamma =\dfrac{1}{2}\times 1\times (-2)=-1=\dfrac{-2}{2}=\dfrac{-d}{a}$

ii. ${{x}^{3}}-4{{x}^{2}}+5x-2$; $2,1,1$

Ans: Comparing the given polynomial with $p\left( x \right)=a{{x}^{3}}+b{{x}^{2}}+cx+d$, we get

$a=1,b=-4,c=5$ and $d=-2$.

$p(1)={{(1)}^{3}}-4{{(1)}^{2}}+5(1)-2$

$\Rightarrow 1-4+5-2=0$

$p(2)=2{{(2)}^{3}}-4{{(2)}^{2}}+5(2)-2$

$\Rightarrow 8-16+10-2=0$

$p(1)={{(1)}^{3}}-4{{(1)}^{2}}+5(1)-2$

$\Rightarrow 1-4+5-2=0$

$\therefore 2,1$ and $1$ are the zeroes of ${{x}^{3}}-4{{x}^{2}}+5x-2$.

Now, $\alpha +\beta +\gamma =2+1+1=4=\dfrac{-(-4)}{1}=\dfrac{-b}{a}$.

And $\alpha \beta +\beta \gamma +\gamma \alpha =\left( 2 \right)(1)+(1)(1)+(1)\left( 2 \right)$

$\Rightarrow 2+1+2=\dfrac{5}{1}=\dfrac{c}{a}$

And $\alpha \beta \gamma =2\times 1\times 1=2=\dfrac{-(-2)}{1}=\dfrac{-d}{a}$.

9. Find a cubic polynomial with the sum of the product of its zeroes taken two at a time and the product of its zeroes are $2,-7,-14$  respectively.

Ans: Let the cubic polynomial be $a{{x}^{3}}+b{{x}^{2}}+cx+d$ and its zeros be $\alpha ,\beta $ and $\gamma $ .

Then $\alpha +\beta +\gamma =2=\dfrac{-(-2)}{1}=\dfrac{-b}{a}$ and $\alpha \beta +\beta \gamma +\gamma \alpha $.

$\Rightarrow -7=\dfrac{-7}{1}=\dfrac{c}{a}$

And $\alpha \beta \gamma =-14=\dfrac{-14}{1}=\dfrac{d}{a}$

Here, $a=1,b=-2,c=-7$ and $d=14$.

Hence, cubic polynomial will be ${{x}^{3}}-2{{x}^{2}}-7x+14$.

10. If the zeroes of the polynomial ${{x}^{3}}-3{{x}^{2}}+x+1$ are $a-b,a,a+b$ find $a$ and $b$. 

Ans: Since $(a-b),a,(a+b)$ are the zeroes of the polynomial ${{x}^{3}}-3{{x}^{2}}+3x+1$.

$\therefore \alpha +\beta +\gamma =a-b+a+a+b=\dfrac{-(-3)}{1}=3$

$\Rightarrow 3a=3$

$\Rightarrow a=1$

And $\alpha \beta +\beta \gamma +\gamma \alpha $

$\Rightarrow (a-b)a+a(a+b)+(a+b)(a-b)=\dfrac{1}{1}=1$

$\Rightarrow {{a}^{2}}-ab+{{a}^{2}}+ab+{{a}^{2}}-{{b}^{2}}=1$

$\Rightarrow 3{{a}^{2}}-{{b}^{2}}=1$

$\Rightarrow 3{{(1)}^{2}}-{{b}^{2}}=1[\because a=1]$

$\Rightarrow 3-{{b}^{2}}=1$

$\Rightarrow b=\pm 2$

Hence $a=1$ and $b=\pm 2$.

11. If two zeros of the polynomial ${{x}^{4}}-6{{x}^{3}}-26{{x}^{2}}+138x-35$ are $2\pm \sqrt{3}$ , find the other zeros.

Ans: It is given that the two zeros of the polynomial ${{x}^{4}}-6{{x}^{3}}-26{{x}^{2}}+138x-35$ are $2+\sqrt{3}$ and $2-\sqrt{3}$.

Therefore, the sum of zeros is $2+\sqrt{3}+2-\sqrt{3}=4$

and product of the zeros is $1$. 

Hence,$({{x}^{2}}-4x+1)$ is the factor of ${{x}^{4}}-6{{x}^{3}}-26{{x}^{2}}+138x-35$.

So, the other factors can be determined by:

\[\begin{matrix} &\quad x^2-4x+1\overset{x^2-2x-35}{\overline{){x^4-6x^3}-26x^2+138x-35}}\\ &\underline{\;x^4\;-4x^3\;+\;x^2}\\ &\hspace{3.5cm}-2{{x}^{3}}-27{{x}^{2}}+138x-35\\ &\hspace{2.3cm}\underline{-2x^3\;+\;8x^2\;- \;2x} \\ &\hspace{4.8cm}-35x^2+140x-35 \\ &\hspace{4.8cm}\underline{-35x^2+140x-35} \\ &\hspace{7cm}\underline{\qquad\quad0\quad} \end{matrix}\]

Now,

$\Rightarrow {{x}^{2}}-2x-35={{x}^{2}}-7x+5x-35$ 

$\Rightarrow x(x-7)+5(x-7)$

$\Rightarrow {{x}^{2}}-2x-35=(x+5)(x-7)$

Thus, the zeros are

$x=7$ and $x=-5$

\[\therefore \] The other two zeros are $7$ and $-5$.

12. If the polynomial ${{x}^{4}}-6{{x}^{3}}+16{{x}^{2}}-25x+10$ is divided by another polynomial ${{x}^{2}}-2x+k$ , the remainder comes out to be $x+a$ , find ‘$k$’ and ‘$a$’.

Ans: Dividing ${{x}^{4}}-6{{x}^{3}}+16{{x}^{2}}-25x+10$ from ${{x}^{2}}-2x+k$, we get: 

\[\begin{matrix} & x^2-2x+k\overset{x^2-4x+(8-k)}{\overline{){x^4-6x^3}+16x^2-25x+10}}\\ & \underline{x^4-2x^3+kx^2}\\ & \hspace{4cm}-4{{x}^{3}}+(16-k){{x}^{2}}-25x+10\\ & \hspace{2.6cm}\underline{-4x^3\;+\;8x^2\;- \;4kx} \\ & \hspace{5.6cm}(8-k)x^2+(4k-25)x+10 \\ & \hspace{7cm}\underline{(8-k)x^2-(16-2k)x+(8k-k^2)} \\ &\hspace{7cm}\underline{\qquad\quad(2k-9)x+(k^2-8k+10)\quad} \end{matrix}\]

But remainder is given to be $(x+a)$ 

Thus, equating the coefficient of $x$ and constant term, we have

$2k-9=1$ 

$\Rightarrow 2k=10$ 

$\Rightarrow k=5$ 

Also, $2k-8k+10=a$ 

$\Rightarrow 25-40+10=a$ 

$\Rightarrow -5=a$

Hence, $k=5$ and $\text{a}=-5$.

Important Questions for Class 10 Maths Polynomials Free PDF Download

Important questions of chapter 2 maths class 10 contain different types of questions that have a higher chance of coming in your examinations. The chapter Polynomials is a part of your Unit-II which has the highest weightage among all other Units. So prepare the chapter well using the pdf for important questions of chapter 2 maths class 10. The Unit-wise weightage is given below:

Class 10 Maths Unit Wise Weightage

The examination is for a total of 80 marks and is divided into four sections. The examination pattern is given below:

Polynomials Important Questions Class 10

Class 10 is an important milestone in a student’s life as it is after this class you will have to make an important career-related decision. To open up all the opportUnities for yourself, you will have to score well in your Class 10  examinations. To score well in your mathematics exam,  you will have to put in consistent efforts. Prepare each topic well and practice solving important questions and sample papers.

The sub-topics discussed in detail in the chapter- Polynomials are as follows.

• Degree of the polynomial.

• Types of polynomials.

• Zeroes of the polynomial.

• Relationship between Coefficients of the polynomial and its roots.

• Division of a polynomial with another polynomial using the long division method.

Degree of the Polynomial

Degree of the polynomial is defined by the highest power of the polynomial. The degree is a representation method of the polynomial. For a polynomial p(x), which is a polynomial of a single variable, the degree is depicted by:

p(x) = x + 1, is a polynomial of degree 1.

p(x) = x² - 2x + 1 is a polynomial of degree 2.

p(x) = x³ -2x is a polynomial of degree 3.

p(x) = 2x³ - 3x² - 3x + 2 is a polynomial of degree 4.

p(x) = 4x⁵ + x² - 2x + 1 is a polynomial of degree 5.

Types of Polynomials Based Upon the Degree of the Polynomial

Degree of the polynomial refers to the highest power of the variable. Depending upon the degree of the polynomial, it can be categorised into:

1. Linear Polynomial - Polynomial of degree one. Ex- 5x - 1.

2. Quadratic Polynomial - Polynomial of the second degree.  Ex- x² + 2x.

3. Cubic Polynomial - Polynomial of degree three. Ex- x³ - 2x² + 4x + 1.

4. Quartic Polynomial - Polynomial of the fourth degree. Ex- 2x⁴ - 3x².

Types of Polynomials Based Upon the Number of Terms

Polynomials are algebraic expressions made up of terms that are connected using mathematical operators. Polynomials can also be differentiated based upon the number of terms:

• Monomial - Polynomials with only a single term. Ex -  4x², -2x, 4 etc.

• Binomial - Polynomials with two terms. Ex - x + 4, x³ - 2x etc.

• Trinomial - Polynomial made up of three terms. Ex - x² - 2x + 1 etc.

Zeros of the Polynomial

Zeros of a polynomial are the values of the variable which satisfy the polynomial function, P(x) = 0. The number of zeros of a polynomial is dependent upon the degree of the polynomial.

A polynomial of degree 1 has only one zero.

A polynomial of degree 2 has two zeros.

A polynomial of degree 3 has 3 zeros.

Zero of a linear polynomial is given by the formula:

$\text{Zero of the polynomial }= -\dfrac{\text{constant}}{\text{coefficient of }x}$

Zero of a quadratic polynomial can be found using hit and trial method but often this is tiresome so we use the quadratic formula to find the zeros of a quadratic polynomial.

For a quadratic polynomial $ax^2 + bx + c$. The zeros of the polynomial are:

\[x = (\frac{-b \pm \sqrt{b^{2} - 4ac}}{2a}\]

Relationship Between Zeroes of the Polynomial and the Coefficients

For a polynomial $ax^2 + bx + c$, Let and be the roots of the equation.

$\alpha + \beta = -\dfrac{b}{a}$

$\text{Sum of the roots }= -\dfrac{\text{coefficient of }x}{\dfrac{coefficient of }x^2}$

$\alpha \beta = \dfrac{c}{a}$

$\text{Product of the roots }= \dfrac{\text{constant term}}{\text{coefficient of }x^2}$

For a polynomial $ax^3 + bx^2 + cx + d$, Let , and be the roots of the equation.

$\alpha + \beta + \gamma = -\dfrac{b}{z}$

$\alpha \beta + \beta \gamma + \gamma \alpha = \dfrac{c]{a}$

$\alpha \beta \gamma = -\dfrac{d}{a}$

Download the list of important questions for class 10 maths polynomials to practice questions from each of the topics. Solving different types of questions from each sub-topic will make the students familiar in solving complex problems if they come in your examinations.

List of Important Questions for Class 10 Maths Chapter 2

Practising is key when it comes to mathematics. The more you practice,  the more you will get familiar with solving problems faster and accurately. The marking scheme used in mathematics is step-wise, so you are awarded marks for every correct step. The pdf will help you in formatting the answers correctly as well.

The list of some of the commonly asked questions in the examination from this chapter are:

1. Find the degree of the polynomial - x² + 12x + 1.

2. Find the zeros of the quadratic polynomial x² - 3x + 2 = 0 using the quadratic formula.

3. Give examples of quadratic and linear polynomials.

4. Find the degree of the polynomial- 10x⁵ + 100x² - 2x + 1000.

5. Find the sum and product of zeros of the following polynomial - x² + 2x - 1.

6. The sum and products of the roots of a quadratic polynomial are 0 and 5 respectively. Find the quadratic polynomial.

7. α and β are the roots of the polynomial f(x) = x² - x - 4. Find the value of the following equation.

$\dfrac{1}{\alpha} + \dfrac{1}{\beta} - \alpha \beta$

8. Divide 6x³ + x² - 26x - 21 by 3x - 7.

9. For a given polynomial - x² - (k + 6)x + 2(2k + 1). Find the value of k such that the sum of the roots is half the product of zeros.

10. Two zeros of the polynomial x⁴ - 6x³ - 26x² + 138x - 35 are given as $2 \pm \sqrt{3}$. Find the other two zeros of the polynomial.

11. The zeros of the polynomial f(x) = x² + px + q are and .Find the polynomial whose zeros are $(\alpha + \beta}^2$ and $(\alpha - \beta)^2$.

12. Is the degree of the following polynomial $\dfrac{1}{x^3 - 2x)$?

13. Divide x⁴ - 5x + 6 by 2 - x².

Benefits of Class 10th Maths Chapter 2 Important Questions

CBSE class 10 maths polynomials important questions pdf is designed to help the students in the preparation of their examinations. The list is accurate and reliable as subject experts make them. The pdf can also be used as a revision tool that will allow you to practice all the important questions from the Chapter- Polynomials. The chapter has a good weightage in the examinations so students should prepare these questions carefully to score well.

The benefits of chapter 2 class 10 maths important questions are given below:

• The pdf is prepared as per the examination guidelines by researching through previous year question papers.

• The list of important questions is prepared by our subject experts who have years of experience in teaching.

• The list is designed to give you a clear picture of what type of questions you can expect in your question paper.

• The pdf will help in highlighting your weak points so that you can bolster them.

• Practising important questions will help in improving your score in your examinations.

Conclusion

CBSE class 10 maths chapter 2 important questions pdf is a must-have tool in the student’s preparation toolkit for their final examinations. These questions will help you in scoring well and obtaining an in-depth understanding of the concepts. Practising these questions daily will increase your mathematics aptitude and you will develop a habit of practising mathematical problems daily which will help you in your higher classes as well.

Related Study Materials for Class 10 Maths Chapter 2 Polynomials

CBSE Class 10 Maths Chapter-wise Important Questions

Additional Study Materials for Class 10 Maths